利用CUR矩阵分解提高特征选择与矩阵恢复能力
2017-05-24雷恒鑫刘惊雷
雷恒鑫,刘惊雷
(烟台大学 计算机与控制工程学院,山东 烟台 264005) (*通信作者电子邮箱jinglei_liu@sina.com)
利用CUR矩阵分解提高特征选择与矩阵恢复能力
雷恒鑫,刘惊雷*
(烟台大学 计算机与控制工程学院,山东 烟台 264005) (*通信作者电子邮箱jinglei_liu@sina.com)
针对在规模庞大的数据中不能快速准确地选择用户和产品的特征以及不能准确预测用户行为偏好的问题,提出一种CUR矩阵分解方法。该方法是从原始矩阵中选取少量列构成C矩阵,选取少量行构成R矩阵,然后利用正交三角分解(QR)构造U矩阵。分解后的C矩阵和R矩阵分别是用户和产品的特征矩阵,并且C和R矩阵是由真实的数据构成的,因此能够分析出具体的用户和产品特征;为了能够比较准确地预测用户的行为偏好,改进了CUR算法,使其在矩阵恢复方面有更高的稳定性和准确性。最后在真实的数据集(Netflix数据集)上的实验表明,与传统的奇异值分解、主成分分析等矩阵分解方法相比:在特征选择方面,CUR矩阵分解方法具有较高的准确度和很好的可解释性;在矩阵恢复方面,改进的CUR矩阵分解方法具有较高的稳定性和精确度,其准确度能达到90%以上。CUR矩阵分解在推荐系统对用户的推荐方面和交通系统预测交通流量方面有重要的应用价值。
行列联合选择算法;特征选择;矩阵恢复;可解释性;稳定性
0 引言
现实生活中,人们经常对所购买的产品进行评价。大多数商家都会在顾客购买完商品后,要求顾客对商品进行打分和评论。系统收集顾客对商品的打分信息后会生成User-Item评分矩阵,然后对这个矩阵进行分析处理,选择出用户的主要特征和产品的主要特征,以及某一类用户主要喜欢产品的哪一类特征。商家拿到这些信息后,就会根据这些特征来调整库存,系统就会向用户推荐他们喜欢的产品等一些活动。在这一系列的分析当中,特征选择和预测用户的偏好尤为重要[1]。无论是调整库存还是预测用户的偏好都是根据特征选择的结果来进行的[2-3],当预测用户偏好的时候,可以对User-Item矩阵进行分解。
传统的矩阵分解方法,例如奇异值分解(Singular Value Decomposition, SVD)[4-5]、SVD++[6-7]以及主成分分析(Principal Component Analysis, PCA)[8-10]虽然能够将高维的User-Item评分矩阵分解成为低维的用户矩阵和产品矩阵,但是分解出来的结果不具有可解释性,因为分解出来的用户矩阵和产品矩阵的每一行和每一列都不是原始的数值,无法用现实生活中的概念来解释,也不能用实际的概念给每一行每一列命名,只能理解为潜在语义空间,因此分解后矩阵的可解释性非常差。另外,因为分解后的矩阵中的数值并不是原始数据,通过矩阵恢复来预测用户偏好的稳定性和准确度也较差。
本文主要利用行列联合选择(Column Union Row, CUR)算法实现特征选择,利用改进的CUR算法实现矩阵恢复。本文具有如下特点和贡献:
1)通过CUR特征选择方法,能够从原始的User-Item评分矩阵选择少量的行和列,进而可以选择出用户和产品的主要特征,其构造的C和R两个矩阵是由真实的数据构成,所以能够通过C和R矩阵分析出具体的特征,具有较好的特征选择能力、很好的可解释性和较高的准确度。
2)改进了CUR算法,根据正交三角分解(OrthogonalRotation,QR)具有数值上的稳定性的特点,利用QR分解方法代替原始的广义逆方法,构造矩阵U,提高了CUR算法进行矩阵恢复的准确性和稳定性。
3)通过在电影评分数据集上进行实验,验证了在相同实验条件下,CUR分解进行特征选择的可解释性和特征选择能力比SVD等矩阵分解方法要好,利用改进的CUR进行矩阵恢复,其稳定性和准确性要高于SVD等矩阵分解方法。
1 相关工作
1.1 特征选择的方法和技术
特征选择在很多书里面也叫作变量选择或者属性选择,它能自动选择出不同的属性或者特征。特征选择的本质就是选择一个特征的子集,这个特征的子集几乎涵盖了原始数据的所有特征。特征选择和维度约减(降维)是不同的,虽然两种方法都是在减少数据集特征(属性)的数量,降维是通过创建一个新的特征组合来做的,数据已经被改变。而特征选择是通过排除或者包括特征数据来做的,数据不会被改变。降维的技术主要有主成分分析和奇异值分解[11-13]。特征选择的方法可以帮助创建特征的集合,这个集合几乎可以涵盖原始数据所有的特征,因此可以通过这个集合来分析原始数据的特征。
特征选择的方法可以用来识别和消除不必要的无关的和冗余的数据,特征选择的方法有3种:第一种是过滤方法,过滤特征选择方法应用统计方法来分配每个特征的得分,每个特征根据得分和排名来确定是否可以被选择;第二种方法是包装方法,包装方法考虑将一组特征作为一个搜索问题,搜索方法有使用启发式的爬山算法或者最佳优先搜索算法等,在搜索过程中表现优异的特征子集会被选中;第三种方法是嵌入式方法,嵌入式特征选择方法的最主要的特点是当模型被创建的时候,这个被创建的模型是准确的,最常见的一种特征选择方法是正则化方法。
本文采用的CUR特征选择方法[14-16]是第一种,即属于过滤方法,CUR特征选择方法就是利用统计影响力评分来计算每一行和每一列特征的得分,然后根据每一个行(列)特征的得分来决定行(列)是否被选择。通过这一方法,将冗余的数据或者噪声过滤掉,得到比较有代表性的特征的集合,通过这个集合,可以很容易和快速地分析原始数据具有的特征。本文使用CUR矩阵分解把高维数据转到低维空间中,在低维空间[17]中来快速对用户和电影的特征进行选择。
1.2 矩阵恢复
矩阵恢复是最近几年非常流行的压缩感知技术,在推荐系统数字图像处理方面应用得非常广泛。通过分析近几年举办的Netflixprice电影推荐大赛和百度电影推荐大赛以及阿里最近举办的天池大数据竞赛中涉及的推荐算法,发现在进行用户偏好预测的时候,矩阵恢复应用得非常广泛。本文研究的一个方面是利用改进的CUR算法进行矩阵恢复,改进的CUR算法比原始的CUR算法更加稳定。2008年Bell等[18]指出矩阵分解模型是最精确的,而CUR矩阵分解保留了原始的数据,因此利用CUR进行矩阵恢复具有准确性和稳定性。
2 CUR分解的基本概念和相关定义
原始的CUR矩阵分解中构造中间矩阵U的时候需要用到广义逆,所以先给出其定义。
定义1 广义逆。若一般线性方程组:
AX=B,A∈Rm×n,X∈Rn,B∈Rm
(1)
若对任意B,都有X=A+B,则矩阵A+∈Rn×m称为A的广义逆。
简单来说,广义逆矩阵是对逆矩阵的推广。
下面给出CUR分解的基本概念和相关定义,并通过例1加以说明。
定义2 CUR分解。CUR分解就是给定一个矩阵A∈Rm×n,然后从矩阵A里选择c列来构造矩阵C∈Rm×c。从矩阵A里选取r行来构造r行n列的矩阵R,通过C和R矩阵的广义逆来构造矩阵U∈Rc×r:
A≈CUR
(2)
其中:C矩阵是由A矩阵的列所构成,而列包含的是电影的特征/采样,从C矩阵中分析出电影具体的特征。R矩阵是由A矩阵的行所构成,而行包含的是对用户的特征/采样,从R矩阵中分析出用户具体的特征,而U矩阵是表示用户和产品之间的相关性。
图1形象直观地解释了CUR矩阵分解的过程,即从真实矩阵A中通过列和行的特征显著程度选择特征显著的行和列,然后构成C、U和R三个维度比较低的矩阵。通过分析低维矩阵的特征来表示高维矩阵的特征。如果A矩阵代表一个User-Movie评分矩阵,图1表示矩阵A维度较大,不容易分析用户的行为偏好,通过CUR矩阵分解对高维矩阵A进行降维,通过快速分析低维矩阵来快速找到用户的行为偏好,因为CUR矩阵分解是从真实数据中按照特征的显著程度抽取若干行和若干列进行计算的,因此保证了分析结果的准确性和可解释性。
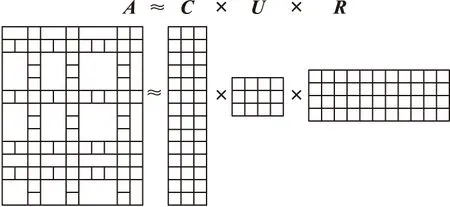
图1 CUR分解示意图
下面再来看一下偏好的类型,偏好包含定性偏好和定量偏好。例如CP-nets就是一种定性条件偏好模型[19],它以序关系o1≻o2表示o1优于o2;而本文采用的是定量模型,即偏好用数值代表(用户对电影的偏好是一个分数,如表1所示)。
为了更好地理解CUR矩阵分解[20-21]的相关内容,给出实例1说明。实例使用的数据集是由Netflix电影公司提供的数据集。为了便于理解、运算和分析,从Netflix数据集选取了少量具有代表性的用户和电影进行CUR分解,通过这个例子,可以看出CUR分解的过程。
例1 如表1所示,矩阵A代表用户对电影进行评分的数据。通过分析CUR矩阵分解的过程,理解CUR矩阵分解的思路和原理。
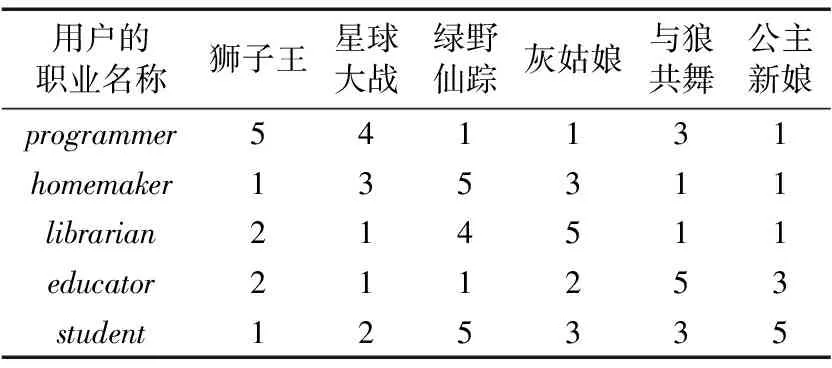
表1 用户-电影评分矩阵
如表1所示,把表中的User-movie评分矩阵称为A。CUR算法要求需要从矩阵A中选取c列来构造矩阵C,假如选取狮子王、灰姑娘、公主新娘这3列,这3列构造出的C矩阵如下所示:
接下来随机地从矩阵A中选取homemaker和student两行,这两行构造出了矩阵R如下所示:

下面构造中间矩阵U。U矩阵是3×2矩阵。构造矩阵U需要用到广义逆,通过上面的方法,构造的U矩阵为:
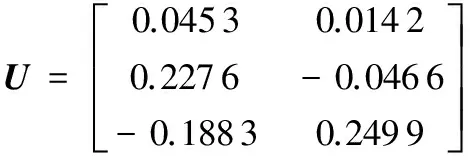
经过上面的步骤,已经随机构造出了矩阵C、U和R。下面对C、U和R这3个矩阵相乘,进行矩阵恢复。
根据表1写出原始矩阵A:


ERROR=‖A-CUR‖F/‖A‖F*100%
(3)
通过计算,两个矩阵的相似度为50.15%,通过上面的这两个矩阵对比可以看到,利用原始的CUR矩阵分解方法进行矩阵恢复的准确度并不高,通过大量的实验发现,这是因为在构造C和R矩阵的时候有时候会把一些“不重要的行或者列”包含进来,相当于C矩阵和R矩阵中包含了一些干扰,因此在利用广义逆求矩阵U时,干扰会进一步扩大,这就会在矩阵恢复的时候出现准确度时好时坏不稳定的状况,因此下面改进了矩阵U的求解方法,借用稳定的QR分解来求解U,因为QR的分解的优点是具有数值的稳定性,大量的实验证明这种方法在构造矩阵U和进行矩阵恢复时准确性和稳定性方面是非常高的。
3 通过CUR进行特征选择和矩阵恢复
本章利用改进的CUR进行特征选择和矩阵恢复,通过例子和大量实验证实了改进的CUR能够提高特征选择和矩阵恢复能力,改进后的CUR算法比原始的CUR算法在矩阵恢复方面更加地稳定和准确。
3.1 利用统计影响力评分提高特征选择能力
从原始数据矩阵User-Item矩阵中选取列和行来构造C和R矩阵时,为了提高特征选择能力,需要选择具有影响力的特征。比如在选择列的时候[22-23],需要选择特征比较显著的列,这些列在整个电影列中具有较大的影响力,占的权重比较大。同样地,在选择行的时候,需要选择特征比较显著的行,这些行在整个用户行中具有比较大的影响力,占的权重比较大。
下面分析每一列的统计影响力评分如何计算。在线性代数中,原始矩阵的每一列可以用奇异值、左奇异向量和右奇异向量精确地表示:
(4)
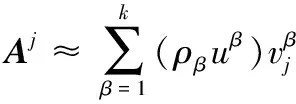
当从A中选择小数量列构造矩阵C的时候,就需要比较将要选择的列在所有电影列中的影响力,也就是特征的显著程度,这时候就需要计算每个列的统计影响力评分,通过统计影响力评分来确定为需要选择哪些特征显著的列,也可以把统计影响力评分理解正则化杠杆效应值。
因为在奇异值分解中,右奇异向量的每一列代表具有同一类特征的电影,因此可以根据右奇异向量来计算每一列的统计影响力评分,也就是每一个电影列特征的显著程度。左奇异向量的每一行代表具有同一类特征的用户,因此可以根据左奇异向量来计算每一行的统计影响力评分,但是为了下面计算简便,也为了节省运算的时间和空间,只计算和存储左奇异向量。在选择行的时候,只需对矩阵作个转置。式(5)是统计影响力评分的定义:
(5)
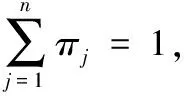
CUR算法提高特征选择能力关键的步骤是利用统计影响力评分进行行列选择,先来介绍一下列选择算法。下面是列选择算法的执行步骤:
算法1 列选择算法。
输入:任意A∈Rm×n,矩阵A的秩k,误差元素。
输出:C∈Rm×c。
1)计算A的前k个右奇异向量v1,v2,…,vk。
2)利用式(4)计算每一列的统计影响力评分。
3)选择统计影响力评分最高的c=O(klgk/ε2)列(c列概率和大于80%)构成矩阵C。
返回:C∈Rm×c。
3.2 改进CUR算法提高矩阵恢复准确性和稳定性
通过大量的实验,发现利用原始的CUR矩阵分解构造矩阵U,也就是通过广义逆矩阵构造矩阵U,进行矩阵恢复的结果非常不准确,因此本文借用成熟稳定的QR分解代替广义逆构造矩阵U,后面的实验结果表明,通过QR分解来构造矩阵U,其矩阵恢复的稳定性和准确性比原始的CUR分解和其他矩阵分解方式要高,因为QR的分解的优点是具有数值的稳定性。算法2描述了矩阵U的构造步骤。
算法2 矩阵U的构造。
输入:A∈Rm×n,r行n列的矩阵R,C∈Rm×c。
输出:U∈Rc×r。
1)对C作QR矩阵分解获得矩阵C的基础列,C=QcRc。
2)对R作QR矩阵分解获得矩阵R的基础行,R=QrRr。
返回:U∈Rc×r
3.3 利用改进的CUR算法进行特征选择和矩阵恢复
CUR算法因为利用了统计影响力评分这个强有力的工具,加上其分解后的矩阵包含的是真实的行和列,数据没有失真,因此其特征选择能力大幅度提高,并且具有非常好的可解释性。而且因为其分解后C和R矩阵保留了原始矩阵的数据,通过改进的CUR进行矩阵恢复,其矩阵恢复的稳定性和准确性大幅度增强。改进的CUR特征选择和矩阵恢复算法的伪代码如算法3所示。
算法3 利用改进CUR进行特征选择和矩阵恢复。

1)先对Netflix数据集进行预处理,将Netflix数据集转成User-Movie评分矩阵A∈Rm×n。
2)对矩阵A运行列选择算法1构造矩阵C。
3)对矩阵AT运行列选择算法1构造矩阵R。
4)利用算法2计算矩阵U。
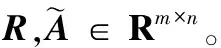
通过在多个数据集上进行实验,证实改进的CUR进行矩阵恢复的稳定性比原始CUR进行矩阵恢复稳定性好。图2是在Netflix电影数据集下随着选择行和列数量的变化,改进的CUR算法与原始的CUR算法的稳定性和误差对比。
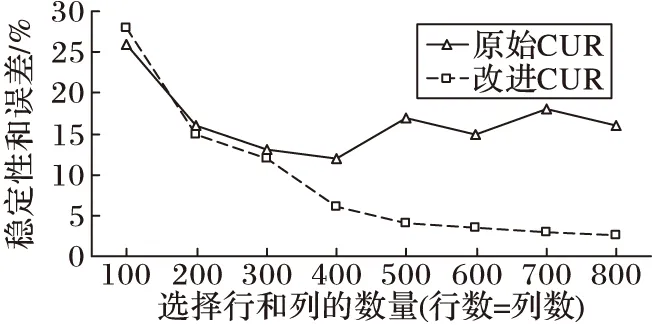
图2 原始CUR和改进CUR稳定性比较
3.4 算法求解实例
例1 从Netflix用户电影评分数据集里选取了具有3个年龄段特征人:10到25岁的青少年Joe和Jim,30到50岁的中年John、Jack和Jill,50岁到80岁的老年Jenny和Jane;同时分别从Netflix数据集里选取了具有3种特征的电影,分别是科幻电影、言情电影和传记电影。对表2中的评分矩阵先执行CUR矩阵分解,然后从分解后的C和R矩阵中进行特征选择,最后进行矩阵的恢复。
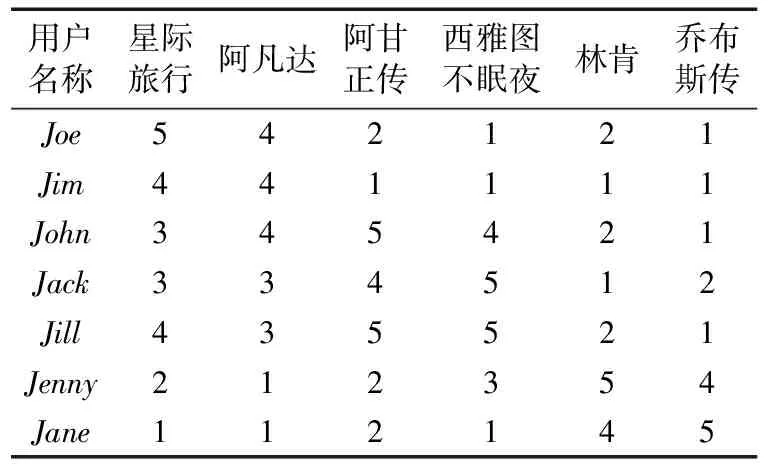
表2 用户-电影评分矩阵
将表2中的矩阵称为矩阵A,然后对矩阵A运行改进CUR特征选择算法进行用户和电影特征的选择。首先,需要从C中选择统计影响力较高的列进行选择,先对矩阵A计算其奇异值,找到右奇异向量,奇异值分解之后的右奇异向量如下所示:
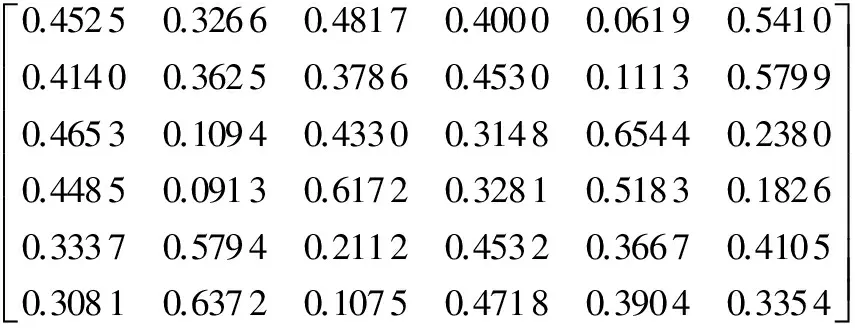
然后根据右奇异向量计算每一列的统计影响力评分,在Matlab上运行改进CUR算法,得出每一列的统计影响力评分分布如图3所示。从图3中可以看出第1列、第4列和第5列的统计影响力评分比较高,说明其特征比较显著,因此,选择第1列、第4列和第5列构成C矩阵:
因为C矩阵中的列是由真实数据构成的,所以可以从真实数据中找到C中的每一列属于哪一个具体的电影,根据真实的电影分析出C中每一列的特征。改进CUR算法通过统计影响力得分提高了特征选择能力,并且根据真实数据构造的C矩阵具有非常好的可解释性。

图3 电影每一列的统计影响力
从图4中可以看出第2行、第4行和第7行的统计影响力评分比较高,说明其特征比较显著,因此,选择第2行、第4行和第7行构成R矩阵:

因为R矩阵中的行是由真实数据构成的,所以可以从真实数据中找到R中的每一行属于哪一个具体的用户,根据真实的用户分析出R中每一行的特征。改进CUR算法通过统计影响力得分提高了特征选择能力,并且根据真实数据构造的R矩阵具有非常好的可解释性。

图4 用户每一行的统计影响力
下面分析一下C矩阵包含哪些电影的主要特征。因为C矩阵是由真实的数据构成的,根据C矩阵的列和Netflix数据集的电影匹配,得到的结果为:第1列属于科幻类,第4列属于言情类,第5列属于传记类。
然后分析一下R矩阵包含哪些用户的主要特征。因为R矩阵是由真实的数据构成的,根据R矩阵的行和Netflix数据集的用户匹配,会得到第2行用户的年龄是27岁,属于青少年用户;第4行用户的年龄是43岁,属于中年用户;第7行用户的年龄是56岁,属于老年用户。
通过上面这个例子,可以分析出用户和电影的具体特征,这说明CUR特征选择算法确实拥有较高的特征选择和分析能力,这是传统矩阵分解算法所不具有的特点。然后利用改进的CUR和原始的CUR进行矩阵恢复,原始的CUR使用广义逆矩阵方法求U,改进CUR使用QR分解求U,将分解后的C、U和R三个矩阵相乘,比较一下两种方法进行矩阵恢复的准确度。利用式(3)计算改进的CUR矩阵恢复的准确度达到了83.63%。然而通过原始的CUR分解,其矩阵恢复得准确度只有67.27%。所以改进U的构造在矩阵恢复方面是有很明显的效果的。后面的实验也验证了改进的CUR在矩阵恢复方面有较高的准确性和稳定性。
4 CUR算法的性质分析
4.1 算法的时间复杂度分析
定理1 CUR算法的时间复杂度是O(nr2+mc2+(klgk)/ε2)。
证明 CUR算法首先需要计算每一列的统计影响力评分,需要的时间复杂度是O((klgk)/ε2),利用QR矩阵分解求U的时候时间复杂度是O(nr2+mc2),所以CUR算法总的时间复杂度为O(nr2+mc2+(klgk)/ε2)。
证毕。
4.2 算法的空间复杂度分析
定理2 CUR算法的空间复杂度是O(mc+rn+cr)。
证明 当CUR算法构造C矩阵和R矩阵的时候,需要将c列r行调入内存中,因此构造C矩阵需要O(mc)的空间,构造R矩阵需要O(rn)的空间,构造U矩阵需要O(cr)的空间,因此该算法的空间复杂度为O(mc+rn+cr)。
证毕。
5 实验环境、结果与分析
本章通过公开的可获得的真实数据集进行测试,并且对已经存在的偏好特征提取算法(SVD,PCA,SVD++)进行比较。
5.1 实验环境
本文实验是在一台计算机上进行的,计算机系统是Windows7 64位的操作系统,配有8GBDDR3内存和主频为2.8GHz的IntelPentiumCPU,使用的软件是Matlab7.0。每个实验重复10次,取平均结果为最终实验结果。
5.2 数据集
实验使用著名电影公司Netflix提供的数据集进行测试,Netflix数据集包含480 189个用户,17 770部电影,100 480 507条评分记录。利用这个数据集对改进的CUR算法以及已知的矩阵分解算法的特征选择性能和矩阵恢复的稳定性及准确性进行评估。
5.3 实验设置
为了说明CUR算法在特征选择和矩阵恢复方面的准确性和稳定性,把CUR算法和下面三种已经存在的特征提取和矩阵恢复算法进行比较。
1)SVD:SVD是主要的特征构造方式。它通过矩阵分解的方式,将数据从高维空间映射到低维空间,对数据进行降维。
2)SVD++:SVD的一种改进算法,SVD算法是指在SVD的基础上引入隐式反馈,使用用户的历史浏览数据、用户历史评分数据、电影的历史浏览数据和电影的历史评分数据等作为新的参数。
3)PCA:PCA是最主要的一种特征提取方式。它通过特征分解能够得到每一个维度对于整个数据的最小均方差的贡献程度,从而定量判断每一维对于数据所包含信息的贡献度。然后保留最主要的一些维度,抛弃一些不显著的维度,从而实现对数据进行降维。
5.4 实验过程
5.4.1 通过CUR进行特征选择
所使用的Netflix数据集包含17 770个用户和100 480 507部电影,因为所使用的计算机内存有限,所以选取了700个用户和1 000部电影的评分。对700×1 000的评分矩阵运行CUR特征选择算法,首先计算电影的统计影响力评分,也就是看看电影有哪些主要的特征,通过程序计算出统计影响力评分最高的17列的概率和大于80%,因此这17列是所有特征列中最主要的,图5也可以看出只有很少的列统计影响力评分很高。
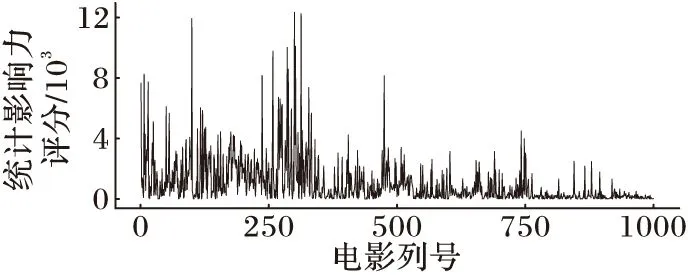
图5 电影每一列的统计影响力分布
如图5所示,除了图中17个特征列比较突出外,其余列的特征(统计影响力评分)不显著,因此就把这17个特征列从原始矩阵中抽取出来构成矩阵C。
矩阵C的列就代表了1 000部电影几乎所有的特征。因为电影公司Netflix在提供数据集的同时也提供了2份文件,1份文件包含了这1 000部电影的信息,1份文件包含了这700个用户的信息。因为矩阵C是由原始数据构成的,每一列对应的是一部真实的电影,将矩阵C的每一列通过和真实的电影信息比对,就能发现电影的具体特征。图6就是和真实的电影信息相比较之后分析出的具体特征,而传统的SVD或者SVD++是无法获取具体特征的。从条形图中只看到9个特征,而不是17个特征。为了保证所选的列能够反映所有列的特征,CUR多选择了一些列,从而提高选择的精度。
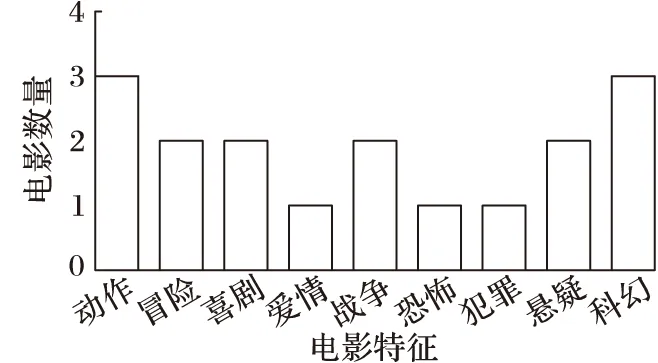
图6 通过CUR选择出的电影的具体特征
然后再计算用户的统计影响力评分,也就是看看用户有哪些主要的特征,通过程序计算出统计影响力评分最高的10行的概率和大于80%,因此这10行是所有特征行中最主要的,图7也可以看出只有很少的行统计影响力评分很高。
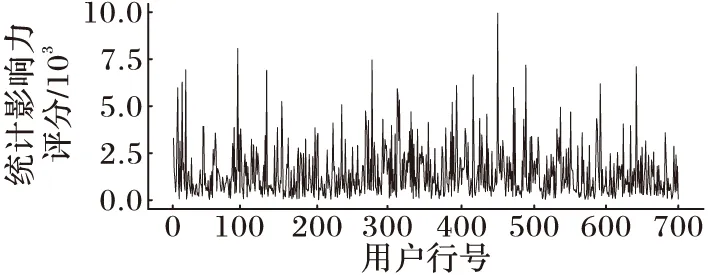
图7 用户每一行的统计影响力分布
如图7所示,除了图中的10个特征行比较突出外,其余行的特征不显著,因此就把这10个特征行从原始矩阵中抽取出来构成矩阵R。因为矩阵R是由原始数据构成的,每一行对应的是一个真实的用户,将矩阵R的每一行通过和真实的用户信息比对,就能发现用户的具体特征。图8就是和真实的用户信息相比较之后分析出的具体特征。
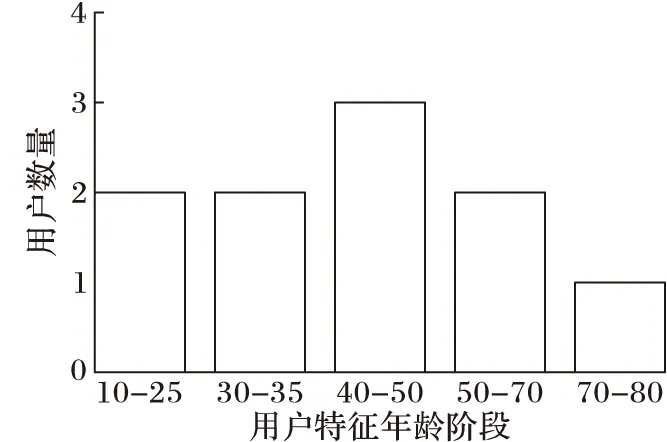
图8 通过CUR选择出的用户的具体特征
从条形图中只看到5个特征,但是原来选择了10行,那是因为CUR在选择具有显著特征的行的时候为了保证所选的行能够代表所有列的特征,所以多选择了一小部分,也可以理解为是为了满足精度的要求。
下面在同样规模的Netflix数据下用PCA进行用户特征的选择发现直接对原始数据直接执行PCA只能找出少数2个特征,第一个特征的贡献率为72%,第二个特征的贡献率为14%,这两个特征的贡献率的和达到了86%,其他特征贡献率极小,PCA给忽略了。那是因为PCA将所有的样本(特征向量集合)作为一个整体对待,去寻找一个均方误差最小意义下的最优线性映射投影,而忽略了类别属性,而它所忽略的投影方向有可能刚好包含了重要的可分性信息,因此使用PCA会忽略掉很多信息。
下面在同样规模的Netflix数据下用PCA进行电影特征的选择发现对原始数据直接执行PCA只能找出少数3个特征,第一个特征的贡献率为60%,第二个特征的贡献率为24%,第三个特征的贡献率为11%,这三个特征的贡献率的和达到了95%,其他特征贡献率极小,PCA给忽略了。原因也是因为PCA忽略了类别属性,导致使用PCA会忽略掉很多信息。
表3展示了在Netflix数据集上,在相同的实验条件下,通过运行CUR、SVD、PCA和SVD++四种矩阵分解方法的运行时间和误差率对比。
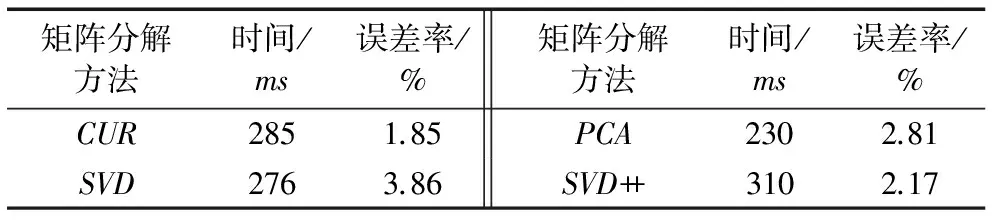
表3 不同矩阵分解方法运行时间和误差率比较
5.4.2 通过改进的CUR进行矩阵恢复
使用改进的CUR分解在Netflix电影数据集上进行矩阵恢复。下面是在Netflix电影数据集上进行恢复,不同的矩阵分解方法进行恢复的稳定性和准确度对比。图9展示了,在Netflix数据集上,CUR、PCA、SVD和SVD++恢复的精确度的变化。从图9中可以看到,随着矩阵规模的增加,改进的CUR分解比PCA等矩阵分解的精确度高,在稳定性方面改进的CUR分解波动比SVD等矩阵分解的波动要小,其稳定性比较高。
5.5 结果
通过上面的实验,可以发现用CUR特征选择算法能够从数据集中比较准确的选取具有较高统计影响力的特征,并且在选取特征行和特征列之后,通过Netflix数据集给出了用户和电影的具体信息,能够分析出选取的特征行和特征列有哪些具体的特征,具有非常好的可解释性。通过改进的CUR进行矩阵恢复,与其他矩阵分解算法相比,其结果具有较高的稳定性和精确度,因此改进的CUR特征选择和矩阵恢复算法在推荐系统方面的前景非常广阔。
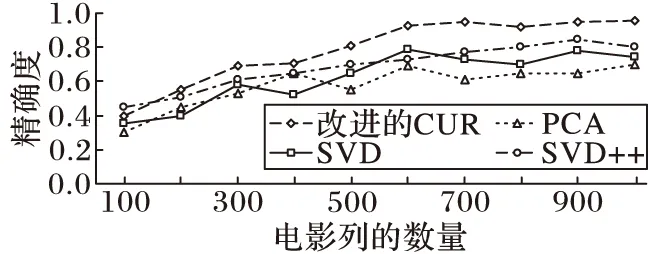
图9 4种矩阵分解方法精确度的变化
6 结语
CUR算法在选取行列的时候是根据行列的实际情况比较智能地进行选择,在机器学习方面,可以理解为在选取行列的时候,CUR算法主动学习和判断电影列的统计影响力来判断电影特征的显著程度,然后根据电影特征的显著程度智能地从电影列中进行抓取,所以构造出的C(R)矩阵也反映了电影(用户)的现实特征,通过分析C(R)矩阵就可以选择出电影(用户)的特征,并且因为C(R)矩阵是由真实的行列构成,因此将C(R)矩阵中的行列数据和Netflix数据集相比对就能够确定用户和电影的具体特征。在矩阵恢复方面,改进的CUR稳定性和精确性都有了明显提升,在进行推荐也就是预测用户偏好的时候,利用改进的CUR算法具有较高的稳定性和精确性。
未来的工作包括:1)CUR算法在面对大规模数据的时候拥有自己的优势,比如快速、准确、具有良好的可解释性,弥补了PCA在面对大规模数据的时候误差较高的不足,但是因为用到了奇异值分解,所以运行时间上可能会稍微逊色一点,因此,接下来会把CUR特征选择算法改进成并行算法,提高CUR算法的运行速度。2)该CUR算法在对原始矩阵的行列进行选择的时候,因为原始用户-电影评分矩阵很稀疏,选出的行和列大部分都存在很多缺失值,对缺失值的填充数值不同,近似的情况以及准确度也不相同,因此,接下来的工作需要探索填充缺失值的方法有哪些,以及如何对缺失值进行填充才能使得CUR矩阵分解的准确度更高。
)
[1]BUSA-FEKETER,SZÖRÉNYIB,WENGP,etal.Preference-basedreinforcementlearning:evolutionarydirectpolicysearchusingapreference-basedracingalgorithm[J].MachineLearning, 2014, 97(3): 327-351.
[2]BOBADILLAJ,ORTEGAF,HERNANDOA.Recommendersystemssurvey[J].Knowledge-BasedSystems, 2013, 46(1): 109-132.
[3] 吴金龙.NetflixPrize中的协同过滤算法[D].北京:北京大学,2010:7-10.(WUJL,CollaborativefilteringalgorithminPrizeNetflix[D].Beijing:PekingUniversity, 2010:7-10.)
[4]GERBRANDSJJ.OntherelationshipsbetweenSVD,KLTandPCA[J].PatternRecognition, 1981, 14(1/2/3/4/5/6): 375-381.
[5]SHNAYDERMANA,GUSEVA,ESKICIOGLUAM.AnSVD-basedgrayscaleimagequalitymeasureforlocalandglobalassessment[J].IEEETransactionsonImageProcessing, 2006, 15(2): 422-429.
[6]KUMARR,VERMABK,RASTOGISS.SocialpopularitybasedSVD++recommendersystem[J].InternationalJournalofComputerApplications, 2014, 87(14): 33-37.
[7]JIAY,ZHANGC,LUQ,etal.Users’brandspreferencebasedonSVD++inrecommendersystems[C]//Proceedingsofthe2014IEEEWorkshoponAdvancedResearchandTechnologyinIndustryApplications.Piscataway,NJ:IEEE, 2014: 1175-1178.
[8]GAOC,ZHOUHH.Rate-optimalposteriorcontractionforsparsePCA[J].TheAnnalsofStatistics, 2015, 43(2): 785-818.
[9]BERTOLINIAC,SCHIOZERDJ.Principalcomponentanalysisforreservoiruncertaintyreduction[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering, 2016, 38(4):1345-1355.
[10]XUF,GUG,KONGX,etal.Objecttrackingbasedontwo-dimensionalPCA[J].OpticalReview, 2016, 23(2): 231-243.
[11]WATKINSDS.FundamentalsofMatrixComputations[M].NewYork:JohnWiley&Sons, 1991: 2-30.
[12]ACHLIOPTASD,MCSHERRYF.Fastcomputationoflow-rankmatrixapproximations[C]//Proceedingsofthe33rdAnnualACMSymposiumonTheoryofComputing.NewYork:ACM, 2001: 611-618.
[13]PFINGSTNERJ,SCHULTED,SNUVERINKJ,etal.SVD-basedfilterdesignforthetrajectoryfeedbackofCLIC[EB/OL]. [2016- 03- 10].http://epaper.kek.jp/IPAC2011/papers/mopo014.pdf.
[14]DRINEASP,MAHONEYMW,MUTHUKRISHNANS.Relative-errorCURmatrixdecompositions[J].SIAMJournalonMatrixAnalysisandApplications, 2008, 30(2): 844-881.
[15]BOUTSIDISC,WOODRUFFDP.OptimalCURmatrixdecompositions[C]//Proceedingsofthe46thAnnualACMSymposiumonTheoryofComputing.NewYork:ACM, 2014:353-362.
[16]BIENJ,XUY,MAHONEYMW.CURfromasparseoptimizationviewpoint[EB/OL]. [2016- 03- 08].http://www.stat.berkeley.edu/~mmahoney/pubs/cur-spca.pdf.
[17]WANGL,REGEM,DONGM,etal.Low-rankkernelmatrixfactorizationforlargescaleevolutionaryclustering[J].IEEETransactionsonKnowledgeandDataEngineering, 2012, 24(6): 1036-1050.
[18]BELLRM,KORENY,VOLINSKYC.TheBellKor2008solutiontotheNetflixPrize[EB/OL]. [2016- 02- 21].http://xueshu.baidu.com/s?wd=paperuri%3A%289ef8f488c3613e6a70daca0f02435bb8%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Bjsessionid%3D3DFEC03FEB7FC3D400E97763E310721E%3Fdoi%3D10.1.1.448.222%26rep%3Drep1%26type%3Dpdf&ie=utf-8&sc_us=13947115770219594334.
[19] 刘惊雷.CP-nets及其表达能力研究[J].自动化学报,2011,37(3):290-302.(LIUJL.CP-netsandstudyofexpressionability[J].ActaAutomaticaSinica, 2011, 37(3): 290-302.)[20] WANG S, ZHANG Z. Improving CUR matrix decomposition and the Nyström approximation via adaptive sampling [J]. Journal of Machine Learning Research, 2013, 14(1): 2729-2769.
[21] WEIMER M, KARATZOGLOU A, SMOLA A. Improving maximum margin matrix factorization [J]. Machine Learning, 2008, 72(3): 263-276.
[22] GURUSWAMI V, SINOP A K. Optimal column-based low-rank matrix reconstruction [C] // Proceedings of the 23rd Annual ACM-SIAM Symposium on Discrete Algorithms. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2012: 1207-1214.
[23] BOUTSIDIS C, DRINEAS P, MAGDON-ISMAIL M. Near-optimal column-based matrix reconstruction [C]// Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science. Washington, DC: IEEE Computer Society, 2011: 305-314.
This work is partially supported by the National Natural Science Foundation of China (61572419, 61572418, 61403328, 61403329), the Natural Science Foundation of Shandong Province (ZR2014FQ016, ZR2014FQ026, 2015GSF115009, ZR2013FM011).
LEI Hengxin, bron in 1993, M. S. candidate. His research interests include the matrix decomposition and its application.
LIU Jinglei, born in 1970, M. S., associate professor. His research interests include artificial intelligence and theoretical computer science.
Improving feature selection and matrix recovery ability by CUR matrix decomposition
LEI Hengxin, LIU Jinglei*
(SchoolofComputerandControlEngineering,YantaiUniversity,YantaiShandong264005,China)
To solve the problem that users and products can not be accurately selected in large data sets, and the problem that user behavior preference can not be predicted accurately, a new method of CUR (Column Union Row) matrix decomposition was proposed. A small number of columns were selected from the original matrix to form the matrixC,andasmallnumberofrowswereselectedtoformthematrixR.Then,thematrixUwasconstructedbyOrthogonalRotation(QR)matrixdecomposition.ThematrixesCandRwerefeaturematrixesofusersandproductsrespectively,whichwerecomposedofrealdata,andenabledtoreflectthedetailedcharactersofbothusersaswellasproducts.Inordertopredictbehavioralpreferencesofusersaccurately,theauthorsimprovedtheCURalgorithminthispaper,endowingitwithgreaterstabilityandaccuracyintermsofmatrixrecovery.Lastly,theexperimentbasedonrealdataset(Netflixdataset)indicatesthat,comparedwithtraditionalsingularvaluedecomposition,principalcomponentanalysisandothermatrixdecompositionmethods,theCURmatrixdecompositionalgorithmhashigheraccuracyaswellasbetterinterpretabilityintermsoffeatureselection,asformatrixrecovery,theCURmatrixdecompositionalsoshowssuperiorstabilityandaccuracy,withaprecisenessofover90%.TheCURmatrixdecompositionhasagreatapplicationvalueintherecommendersystemandtrafficflowprediction.
Column Union Row (CUR) algorithm; feature selection; matrix recovery; interpretability; stability
2016- 09- 28;
2016- 10- 16。
国家自然科学基金资助项目(61572419, 61572418, 61403328, 61403329);山东省自然科学基金资助项目(ZR2014FQ016, ZR2014FQ026, 2015GSF115009, ZR2013FM011)。
雷恒鑫(1993—),男,山东阳谷人,硕士研究生,主要研究方向: 矩阵分解及其应用; 刘惊雷(1970—),男,山西临猗人,副教授,硕士,CCF会员,主要研究方向:人工智能、理论计算机科学。
1001- 9081(2017)03- 0640- 07
10.11772/j.issn.1001- 9081.2017.03.640
TP
A
