数字化仪表着陆系统发射通道校准算法

冯 翔，张 斌

(空军工程大学 信息与导航学院，西安 710077) (*通信作者电子邮箱fengxiang1029@163.com)

数字化仪表着陆系统发射通道校准算法

冯 翔*，张 斌

(空军工程大学 信息与导航学院，西安 710077) (*通信作者电子邮箱fengxiang1029@163.com)

在对仪表着陆系统(ILS)的数字化改造中，针对仪表着陆系统采用振幅式测角体制，对发射信号的幅度失真敏感的问题，提出了一种数字化仪表着陆系统发射通道校准算法。首先，建立了仪表着陆系统发射端的数学模型，仿真研究了发射通道非线性对仪表着陆系统测角性能的影响；其次,提出了一种在数字化仪表着陆系统发射机中引入反馈回路的发射机结构；最后，通过在基带利用最小均方(LMS)算法求解发射通道的逆模型，并利用该逆模型补偿发射通道的非线性失真，实现了发射通道的校准。仿真结果表明，该算法可以在噪声条件下快速估计出发射通道的逆模型，具有良好的校准性能。

仪表着陆系统；发射通道；反馈回路；最小均方；幅度校准

0 引言

仪表着陆系统(Instrument Landing System, ILS)作为国际标准的飞机着陆引导系统，在二战末期就已投入使用，目前世界上数千个军、民用机场都装配有ILS，同时由于ILS成本低，性能稳定，完全满足了民用航空的要求，在未来很长一段时间都难以替代[1-2]。随着软件无线电技术和数字电子技术的发展，数字化设备的性能不断提升，同时成本显著下降。现役的仪表着陆发射设备采用模拟体制，由于实现方式及精度上的不足有待被数字化ILS取代，同时数字化ILS便于进行功能扩展，有助于实现航空电子系统的综合化，如通信导航识别系统。文献[3]和文献[4]主要研究了基于数字信号处理器(Digital Signal Processor, DSP)与现场可编程门阵列(Field Programmable Gate Array, FPGA)的ILS数字基带信号的生成方法，文献[5]研究了数字化ILS接收机的硬件实现，文献[6]主要研究了ILS的链路级仿真。以上研究为ILS的数字化打下了良好的基础，但对数字化ILS发射通道的校准尚未有研究。由于ILS采用振幅式测角体制，发射波形的幅度失真会对ILS的测角精度产生不良影响，这使得在基带采用相应的数字信号处理算法实现ILS发射通道的校准成为ILS数字化改造中必须解决的问题。

本文在深入分析ILS测角原理、信号格式和现役设备结构的基础上，仿真研究了发射通道非线性对ILS性能的不良影响，提出了一种数字化ILS的发射机结构及发射通道校准算法。该算法在发射机中引入反馈回路，采用最小均方(Least Mean Square, LMS)算法在基带构建发射通道的逆模型用以补偿发射通道的非线性失真，保证了数字化ILS的测角精度。

1 ILS数学模型及测角原理

ILS由航向信标、下滑信标、指点信标及机载接收机组成，为待着陆飞机提供相对跑道中线的方位角信息、相对跑道平面的下滑角信息和距跑道端口的距离指示信息[1-2]。航向信号和下滑信号具有类似的信号格式，都采用双单音(90 Hz,150 Hz)复合调幅体制，是载波加边带信号(Carrier with Side-Bands, CSB)和载波纯边带信号(Side-Bands Only, SBO)在空间的合成。为简练起见，以航向信号为例进行说明。航向信标台发射机主要产生CSB信号和SBO信号，其信号格式[1-2]为：

CSB信号：

UCSB(t)=uCSB(1+m90sinΩ90t+m150sinΩ150t)sinωt

(1)

SBO信号：

USBO(t)=uSBO(m90sinΩ90t-m150sinΩ150t)sinωt

(2)

其中:uCSB、uSBO分别为CSB信号和SBO信号的载波幅度，ω为载波角频率，Ω90、Ω150为90 Hz与150 Hz导航音频信号的角频率，m90和m150分别为90 Hz和150 Hz调制信号的调制度，且m90=m150=m。

为得到系统要求的辐射场型，航向天线需在跑道次着陆端以跑道中线延长线为对称中心安装架设[2]。发射机产生的信号通过天线分配网络馈送给不同的天线，分配网络按一定的振幅和相位关系对CSB和SBO信号进行分配。国产某型仪表着陆设备航向信标天线阵由8副对数周期天线组成，其典型的航向天线阵馈电表如表1[2]所示。

表1 ILS八单元航向天线阵典型馈电表

航向天线辐射的场型及相关信号的频谱合成如图1所示。

图1 航向天线辐射场型及信号合成情况

ILS机载接收机收到的信号是经天线发射的CSB与SBO的空间合成信号，其一般形式[1]为：

e(t)=u(1+M90sinΩ90t+M150sinΩ150t)sin(ωt+Φ)

(3)

令调制度差(DDM)[1-2]为：

DDM=M90-M150

(4)

由图1可知，背对航向天线，在跑道中心线右侧，90 Hz调制音频占优，DDM>0；在跑到中心线左侧，150 Hz调制音频占优，DDM<0；在跑到中线上，两者调制幅度相等，DDM=0[1-2]。在接收端，机载接收机对收到的信号通过包络检波，带通滤波，得到90 Hz和150 Hz音频信号，再将两者送入归一化比幅电路解算出DDM，以DDM的大小为参考驱动一个十字双针指示器指示着陆飞机偏移所测角度基准线的情况，引导飞机安全着陆。

下面对航向天线辐射的空间合成信号建模，如图2所示。

图2 八单元航向信标天线阵

图2中，R1～R4、L1～L4分别表示背对航向天线时在跑道中线延长线右侧和左侧的4个天线，P为天线辐射场中的任意一点，设P点距天线中心距离为ro，与跑到中心线的夹角为θ，第i对左右天线到P点的距离分别为rLi、rRi，第i对天线距天线中心的距离为Di，其馈电幅度为Ai，馈电相位为Φi，电波传播的衰落因子为K。航向天线采用对数周期天线，其方向性函数为F(θ)=cos[π sin(θ)/2]，天线间横向间隔为0.75λ，λ为载波波长[6]。设基带信号为Ei(t)，电波传播速度为光速c，则第i对天线中左侧天线在P点处辐射的信号为：

ePL(t)=K*F(θ)*Ei(t)*sin[ω(t-rLi/c)+Φi]

(5)

右侧天线在P点处辐射的信号为：

ePR(t)=K*F(θ)*Ei(t)*sin[ω(t-rRi/c)+Φi]

(6)

若ro≫Di，则rLi≈r0-Disin(θ)，rLi≈r0+Disin(θ)，则第i对天线在空间P点辐射的CSB信号[6]为：

ePCSB(t)=ePL(t)+ePR(t)=2K*F(θ)Ai(1+m90sinΩ90t+m150sinΩ150t)cos(2πDisinθ/λ)* sin(ωt+Φi-2πro/λ)

(7)

同理可得第i对天线在P点辐射的SBO信号为：

ePSBO(t)=2K*F(θ)Ai(m90sinΩ90t-m150sinΩ150t) cos(2πDisinθ/λ-Φi)*sin(ωt-2πro/λ)

(8)

P点的航向信号为四对天线辐射的CSB、SBO信号的空间合成信号。

2 发射通道非线性对ILS测角性能的影响

造成发射通道非线性的原因是多方面的，但末级高功率放大器的非线性是引起发射信号幅度失真的主要原因，可以利用功放模型近似对发射通道建模，研究发射通道非线性对ILS的影响。当输入信号的带宽较小时，功放的记忆效应可以忽略[7]，由于ILS信号属于窄带信号，所以可以采用典型的无记忆功放模型Saleh模型对功放建模。Saleh模型的幅度和相位特性[8]可以表述为：

(9)

(10)

其中：A(r)、Φ(r)分别为功放的AM/AM、AM/PM特性函数，r为输入信号的幅度；αa、βa、αφ、βφ为模型参数，用于描述功放的非线性强度。

设置功放模型参数为αa=1.5，βa=0.2，αφ=2，βφ=1，对应的功放特性曲线如图3所示，可见该组参数对应的功放模型具有较好的线性度。

图3 功放Saleh模型特性曲线

利用式(7)、(8)对P点的ILS航向信号建模，设K=1，ro=10 km，载波频率fc=108 MHz,θ=3°时P点的合成信号如图4所示。

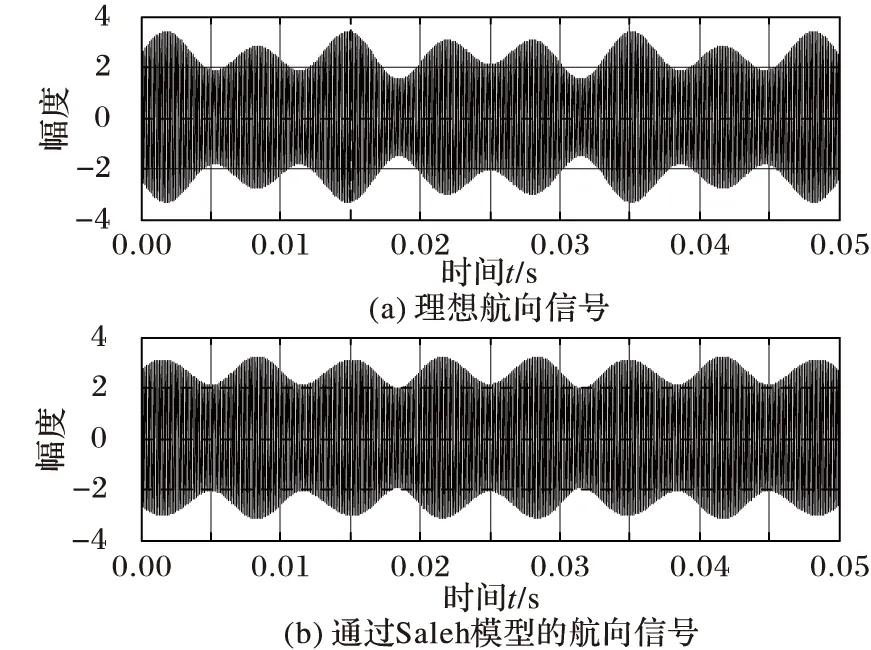
图4 θ=3°时空间P点ILS航向信号

可见通过Saleh模型后，P点合成的ILS航向信号与理想信号相比在波峰与波谷处有一定的幅度失真。

由于ILS信号的调制度是确定的，航向信号每一单音的调制度为20%，下滑信号每一单音的调制度为40%[9]，则调制度差可用下式[5]计算：

(11)

A、B分别为90 Hz和150 Hz音频信号的幅度，m为两音频信号的调制度。

采用希尔伯特原理提取出P点ILS航向信号的包络，然后通过中心频率为90 Hz和150 Hz的带通滤波器滤出90 Hz和150 Hz导航音频信号，利用式(11)计算DDM。系统规定航向信号所提供的DDM为±0.155的边界所确定的区域为航向比例引导扇区(在这个扇区内，DDM值随角度线性变化)，一般在3°～6°[2]，因此，仿真时取P点所处的角度为-6°～6°，解算出的DDM如图5所示。

图5 发射通道非线性对DDM的影响

由图5可知，尽管发射通道的非线性并不明显，但引起的幅度失真会导致接收端解算出的DDM有大的偏差，导致系统无法提供准确的进场角度信息。发射通道的校准是ILS发射机必不可少的功能，现役的模拟体制发射机中也有相应的幅度校准电路，将在下一节介绍。

3 ILS发射机结构及发射通道校准算法

现役某型仪表着陆发射设备基本采用模拟电路，其航向发射机的基本结构如图6所示。

图6 某型航向发射机基本结构

图6中，晶体振荡电路产生的信号，经分频、滤波和放大后得到90 Hz、150 Hz音频信号，然后通过和、差放大器得到所需的“和”(90 Hz+150 Hz)、“差” (90～150 Hz)信号，送入对应的CSB支路和SBO支路。以CSB支路为例说明，和放大器输出的“和”信号被分为两路：一路作为音频基准信号，另一路送入调幅器得到CSB信号，该信号经放大后也分为两路，一路送入天线分配网络，另一路作为CSB信号的取样信号，经检波后得到“和”信号送入比较器与音频基准信号比较，得到预修正的调制控制电压反馈到CSB调制器的控制输入端，修正CSB信号，形成闭环调制以矫正幅度失真，提高调制质量。SBO信号采用与CSB信号同样的修正方法。这种闭环调制的思想是可取的，但这种方法的修正效果很大程度上依赖于调幅器的性能，修正效果有限。

吸收图6中闭环调制的思想在数字化ILS发射机引入反馈回路，即从功率放大器输出端耦合射频信号并变换到基带，配合相应的校准算法实现发射通道的校准，相应的数字化ILS发射机结构如图7所示。

图7 数字化ILS发射机结构

发射机具有CSB与SBO两个支路，它们除共用一片数字信号处理器外相互独立，图7中的非线性系统是指由数模转换器(DA)、调制器、功放、模数转化器(AD)、耦合器、衰减器以及发射通道中的其他非线性元件组成的系统。设该非线性系统的传递函数为P(·)。如果可以通过反馈信号求出该非线性系统的逆模型P-1(·),就可以对发射通道的非线性失真进行科学的补偿。考虑到功放等元件的非线性特性会随着器件温度和器件的老化而改变，所以P(·)表示的系统是时变系统，同时考虑到反馈回路存在引入噪声的可能，这就需要校准算法具有一定的自适应能力，即可以通过学习对P-1(·)进行适当的调整。

下面以CSB支路为例说明校准算法，设经反馈回路送入数字信号处理器的CSB反馈信号为Y(n)，原始CSB基带信号为X(n)，包括反馈回路在内的整个系统引入的加性噪声为n0，采用LMS算法求解P-1(·)，算法结构如图8所示。

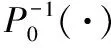
e(n)=X(n)-Z(n)

(12)

Z(n)=WT(n)Y(n)

(13)

LMS算法的代价函数[10]为：

J(W)=E[e2(n)]=E{[X(n)-Z(n)]2}=E[X2(n)]-2W(n)P+WT(n)RW(n)

(14)

式(14)中，P=E[X(n)YT(n)]，R=E[Y(n)YT(n)]，代价函数取得最小值处的W(n)即为所求逆模型的模型参数，可得LMS的维纳解[10]为：

Wo=R-1P

(15)

为便于工程实现采用R、P的瞬时估计值代替统计平均值来估计梯度向量，利用最陡下降法对式(15)维纳解进行搜索，可得W(n)的递推方程[11]为：

W(n+1)=W(n)+2μY(n)e*(n)

(16)

其中：μ为收敛因子，μ越大，算法收敛越快但收敛后的稳态误差也越大；μ越小，算法收敛越慢但稳态性能好[12]。针对这一矛盾可以在算法初始阶段采用较大的μ值提高收敛速度，当算法收敛后再采用较小的μ值来提高收敛后的稳态性能。

4 算法验证

为验证本文所提算法的正确性，利用Matlab对算法进行仿真验证。采用Saleh模型对发射通道建模，模型参数与第2章相同，为αa=1.5，βa=0.2，αφ=2，βφ=1，添加的噪声为高斯白噪声。

实验1 不同信噪比(Signal-to-NoiseRatio,SNR)下算法的稳态性能分析。

1)反馈回路引入少量噪声，发射通道内信噪比良好。设发射通道内的信噪比为20dB，LMS算法的收敛因子为1/256，利用LMS算法构建P-1(·)，仿真得出的LMS算法的误差曲线如图9所示。

图9 LMS算法误差曲线

由图9可知，随着迭代次数的增加算法迅速收敛，稳态误差小于0.06，可见该算法在信噪比为20dB的条件下可以快速估计出发射通道的逆模型，并且具有良好的估计精度。

2)反馈回路耦合端性能不佳，引入大量噪声，发射通道内信噪比不良。设信噪比分别为10dB、5dB与0dB(在发射通道内该信噪比属于极端情况)，LMS算法的收敛因子为1/256，不同信噪比下的LMS算法误差曲线如图10所示。

图10 不同信噪比下LMS算法误差曲线

图10表明，当发射通道的信噪比为10dB和5dB时，算法仍具有较好的稳态性能，稳态误差小于0.1，可以较准确地估计出功放的逆模型。当信噪比为0dB时，算法性能恶化，稳态误差大于0.15且起伏较大，算法存在不收敛的可能。

实验2 不同信噪比下对发射通道的校准能力分析。将逆模型的输出信号作为基带信号，仿真不同信噪比下接收机解算出的DDM值。参数设置与第2章相同，K=1，ro=10 km，载波频率fc=108 MHz,不同信噪比下解算出的DDM如图11所示。

图11 校准后不同信噪比下的DDM

由图11可知，算法在信噪比不低于4dB时，可以对ILS发射通道实现准确的校准，校准后的DDM与理想值偏差很小，最大偏差为0.045 5。当信噪比为3 dB时，DDM的校准值与理想值相比开始出现明显偏差，实际中应保证发射通道的信噪比不低于5 dB。

5 结语

ILS发射机中发射通道的非线性会使DDM出现大的偏差，严重影响系统的性能。仿真结果表明本文所提的算法在信噪比不低于5dB时可以快速准确地求解发射通道的逆模型，对发射通道非线性引起的信号失真具有良好的补偿效果。

References)

[1]张忠兴,李晓明,张景伟,等.无线电导航理论与系统.西安:陕西科学技术出版社,1998:268-279.(ZHANG Z X, LI X M, ZHANG J W, et al. Radio Navigation Theory and System . Xi’an: Shaanxi Science and Technology Press, 1998: 268-279.)

[2]吴德伟.无线电导航系统.北京:电子工业出版社,2015:136-156.(WU D W. Radio Navigation System . Beijing: Publishing House of Electronics Industry, 2015: 136-156.)

[3]孙亚伟，黄家成，元洪波.采用DSP处理器的甚高频全向信标/仪表着陆系统标准信号源.电光与控制，2009，16(7)：92-96.(SUN Y W, HUANG J C, YUAN H B. Standard signal source for VHF omni direction beacon/instrument landing system based on DSP . Electronics Optics and Control, 2009, 16(7): 92-96.)

[4]陈显强.基于FPGA的仪表着陆系统研究与实现.西安:西安电子科技大学，2014.(CHEN X Q. Research and implementation of instrument landing system based on FPGA . Xi’an: Xidian University, 2014.)

[5]杨兴耀.仪表着陆与伏尔导航系统的研究与实现.西安:西安电子科技大学，2010.(YANG X Y. Research and implementation on instrument landing system and VOR navigation receiver . Xi’an: Xidian University, 2010.)

[6]苗强，吴德伟，郭华,等.基于SIMULINK仪表着陆系统链路级仿真.系统仿真学报，2009，21(11)：3259-3263.(MIAO Q, WU D W, GUO H, et al. Link level simulation of instrument landing system based on SIMULINK . Journal of System Simulation, 2009, 21(11): 3259-3263.)

[7]金哲,宋执环,何家铭.无线通信中有记忆放大器的一种预失真方法.电波科学学报，2008，23(1)：85-89.(JIN Z, SONG Z H, HE J M. A predistortion method for power amplifiers with memory in wireless communications . Chinese Journal of Radio Science, 2008, 23(1): 85-89.)

[8]SALEH A A M. Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers . IEEE Transactions on Communications,1981, 29(11): 1715-1720.

[9]International Civil Aviation Organization. Annex 10 to the convention on international civil aviation . 6th Ed. Montreal, Canadad: ICAO, 2006: 33-34.

[10]丁玉美，阔永红，高新波.数字信号处理：时域离散随机信号处理.西安：西安电子科技大学出版社，2002：73-77.(DING Y M, KUO Y H, GAO X B. Digital Signal Processing: Discrete Random Signal Processing . Xi’an: Xidian University Press, 2002: 73-77.)

[11]杜勇.数字滤波器的MATLAB与FPGA实现.北京：电子工业出版社，2015:225-227.(DU Y. Implementation of Digital Filter by MATLAB and FPGA . Beijing: Publishing House of Electronics Industry, 2015: 225-227.)

This work is supported by the National Natural Science Foundation of China (61273048).

FENG Xiang, born in 1991, M. S. candidate. His research interests include radio navigation.

ZHANG Bin, born in 1968, Ph. D., professor. His research interests include radio navigation, satellite navigation.

Transmission channel calibration algorithm for digital instrument landing system

FENG Xiang*, ZHANG Bin

(SchoolofInformationandNavigation,AirForceEngineeringUniversity,Xi’anShaanxi710077,China)

In the digital Instrumentation Landing System (ILS) transformation, aiming at the problem that the ILS adopts the amplitude angle measuring system and is sensitive to the distortion of the amplitude of the transmitted signal, a calibration algorithm of the transmission channel of the digital ILS was proposed. Firstly, the mathematical model of the transmitter’s landing system was established, and the effect of the non-linearity of the transmission channel on the angular performance of the ILS was simulated. Secondly, a transmitter structure with a feedback loop in the digital instrumentation landing system was proposed. Finally, the transmission channel was calibrated by solving the inverse model of the transmission channel in the baseband using the Least Mean Square (LMS) algorithm, and using the inverse model to compensate the nonlinear distortion of the transmission channel. The simulation results show that the proposed algorithm can quickly estimate the inverse model of the transmission channel under noise conditions and has good calibration performance.

Instrument Landing System (ILS); transmission channel; feedback loop; Least Mean Square (LMS);amplitude calibration

2016- 08- 26;

2016- 10- 03。

国家自然科学基金资助项目(61273048)。

冯翔(1991—),男,甘肃天祝人,硕士研究生,主要研究方向:无线电导航; 张斌(1968—),男,河南中牟人，教授,博士,主要研究方向:无线电导航、卫星导航。

1001- 9081(2017)03- 0741- 05

10.11772/j.issn.1001- 9081.2017.03.741

TN967.4

A