具有预制孔隙多孔介质冷冻干燥的多相传递模型

牛利娇，王维，潘思麒，张大为，陈国华



具有预制孔隙多孔介质冷冻干燥的多相传递模型

牛利娇1，王维1，潘思麒2，张大为1，陈国华3

（1大连理工大学化工机械与安全学院，辽宁大连116024；2大连大学环境与化学工程学院，辽宁大连116622；3香港科技大学化学与生物分子工程系，中国香港）

基于局部质量非平衡假设，建立了多相多孔介质热、质耦合传递数学模型，理论验证具有预制孔隙的初始非饱和多孔物料对冷冻干燥过程的强化作用。模型考虑了多孔介质的吸湿效应，构建了3种吸附-解吸平衡关系。模型使用基于有限元法的COMSOL Multiphysics软件平台数值求解，并与实验数据进行了比较。结果表明，初始非饱和冷冻物料能够有效地强化冷冻干燥过程。采用不同函数形式的吸附-解吸平衡关系模拟的干燥曲线均与实验数据非常吻合。通过分析物料内部的饱和度、温度和质量源分布，探讨了初始非饱和物料冷冻干燥过程的传热传质机理。初始非饱和物料的干燥速率控制因素主要是传热。模拟考察环境辐射温度对冷冻干燥过程影响的结果表明，所建模型具有良好的预测能力。

冷冻干燥；非饱和多孔介质；局部质量非平衡；吸附-解吸平衡；传热传质

引 言

与传统的以液体蒸发为机制的干燥方法不同，冷冻干燥是先将湿物料预冷冻固化，然后在低温低压下以升华/解吸的方式去除湿分[1-2]。冷冻干燥主要应用于食品、药品和生物制品等热敏性和高附加值物料的脱水过程[3-5]。目前该技术领域面临的主要问题是干燥速率低、时间长而且能耗大[2,6]。

冷冻干燥是一个复杂的多相热、质耦合传递过程。一方面，热量由湿物料外部向其内部传递；另一方面，物料内部的湿分则通过孔隙由内向外迁移，直到残余湿分降低至满足要求为止。现有的强化冷冻干燥速率的方法主要是强化传热，对传质方面的研究较少[7-8]。Pikal等[9-10]指出，影响干燥速率的重要因素是干区水蒸气的迁移阻力。Nail等[11]认为，水蒸气的传递阻力主要取决于物料在冷冻阶段所形成的冰晶尺寸。Cheng等[12]在探究超声诱导成核对草莓冷冻干燥过程的影响时发现，物料内部小冰晶升华时形成较小的孔隙，增加了水蒸气的传递阻力，从而延长了干燥时间。Chen等[13]首先提出，将液体物料制备成具有初始孔隙的非饱和冷冻物料，再进行干燥以降低过程传质阻力。他们的实验结果表明，初始非饱和物料确实能够显著地强化冷冻干燥过程；在相同的条件下，初始非饱和物料（0=0.28）比饱和物料（0=1.00）的干燥时间缩短了30%以上[14-16]。“具有预制孔隙的多孔物料冷冻干燥”学术思想的实验研究已经取得了预期的成果。因此，进行理论模拟研究来再现和预测这一过程，对于理解冷冻干燥过程机理，优化操作条件以及指导干燥器设计等非常重要[17-18]。此外，数学模型可以用于确定用实验很难测定的变量的分布。相对于实验来说，数值计算的投资要小得多。

在吸湿性多孔介质中，结合水的存在使得简单的热力学相平衡关系已不适用，而应被吸附-解吸平衡关系所替代[6,17]。Halder等[19]指出该平衡关系应该由实验获得。但是由于吸湿多孔介质的多样性和复杂性，基于实验的吸附-解吸平衡关系非常少[20]。Liapis等[21]使用了简单的Langmuir方程来表达吸附-解吸平衡关系。Wang等[22]采用了几种基本初等函数来表达该平衡关系。因此，十分有必要建立通用的吸附-解吸平衡关系。

在多孔介质冷冻干燥过程中，相变现象由吸附等温线的形状和孔隙内有效的热力学条件控制[23]。以前的研究假定，物料孔隙中任意处的冰晶与蒸汽始终处于局部平衡状态[22,24]。近期的研究发现，这个平衡并不总是成立，孔隙中主流蒸汽的压力并不等于其平衡蒸气压[23]，即“局部质量非平衡”。特别是当孔隙尺寸接近100 μm时，这一非平衡现象十分显著[19]。局部质量非平衡假设是指，多孔介质中只有凝聚相（这里是冰）表面的蒸汽压力（或蒸汽浓度）处于平衡状态，而主流蒸汽压力偏离平衡状态。平衡压力与主流蒸汽压力之差（或浓度差）驱动着蒸汽由冰晶表面向主流蒸汽迁移。

本研究基于局部质量非平衡假设，同时认为孔隙中冰晶表面的压力满足吸附-解吸平衡。研究目的是：①推导二维非饱和多孔介质冷冻干燥的热、质耦合多相传递模型；②构建描述吸湿多孔介质冷冻干燥过程的吸附-解吸平衡关系；③在COMSOL Multiphysics平台上对控制方程进行数值求解再现实验条件下的干燥过程，验证模型的可靠性；④分析干燥过程中物料内部饱和度、温度和质量源分布，进而探讨热、质传递机理；⑤预测辐射温度对冷冻干燥过程的影响。

1 数学模型

1.1 问题描述

图1是物料组件示意图，上部是待干的多孔冷冻物料，下部为支撑底盘。物料由固体基质、冰和蒸汽构成，其中冰晶和蒸汽充满了孔隙空间。在干燥过程中，固体基质的质量和体积保持不变，只有冰晶（或蒸汽）在孔隙中的体积分数变化。

模型的基本假设为：固体基质均匀、刚性和各向同性；蒸汽是唯一的气相组分，且为理想气体；各相始终处于局部热平衡状态，Fourier定律在整个区域内适用；冰晶表面的压力与主流蒸汽的压力处于局部质量非平衡状态，蒸汽总体流动的推动力为主流蒸汽的压力梯度，遵循Darcy定律，气体扩散为Knudsen型扩散。

1.2 控制方程

干燥过程中，只有冰晶（或蒸汽）在孔隙中的体积分数，即饱和度（或1−）改变。由于假设局部质量非平衡，冰晶相和蒸汽相的传质方程必须分别表达。单位物料体积内冰晶质量的变化率等于负的质量源项，其质量守恒方程为

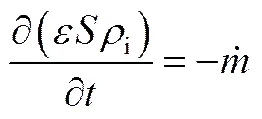
主流蒸汽在压力梯度和浓度梯度的驱动下在孔隙中迁移[25]，其主要机理是Knudsen扩散和总体流动[22]。蒸汽的密度和压力的关系可由理想气体状态方程计算[18]，蒸汽的传质方程为

(2)

其中，蒸汽的总体流动速度由Darcy定律给出

由于各相始终处于局部热平衡，多孔介质中的传热仅用一个方程来表达。传热方程包含传导传热、对流传热和相变传热

(4)

其中，多孔物料的性质是各相性质的体积平均

(c)e= (1-)ss+Sii+(1-)vv(5)

e=(1-)s+Si+(1-)v(6)

在支撑底盘中无质量传递，只有热量传递

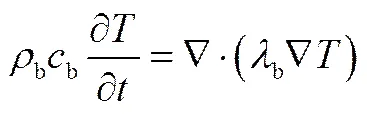
1.3 质量源项

以往研究中常见的多孔介质热、质耦合传递模型都是基于局部质量平衡假设，即式(1)、式(2)合成为一个方程。本研究基于局部质量非平衡假设，并且认为孔隙中冰晶表面的压力满足吸附-解吸平衡。冰晶表面的压力与主流蒸汽的压力并未处于平衡状态，两者之差驱动着蒸汽由冰晶表面向主流蒸汽的迁移。使用统计速率理论，质量源视为正比于这个压力差[26-27]

其中，r为质量非平衡系数，其单位是迁移时间的倒数。质量源与压力差的线性关系只有在偏离平衡不太远时才成立[23]。若质量源为负值，则表示发生了蒸汽凝华或者吸附现象。此外，该方法提供了一个机会来考察非平衡效应对物料内部质量源分布的影响。

1.4 吸附-解吸平衡关系

吸湿物料的蒸气压与湿分在物料中存在的方式有关。物料所含的水分通常分为自由水和结合水[21]。自由水在冷冻阶段冻结成冰，其纯组分相平衡的饱和蒸气压可由Clausius-Clapeyron方程得到。结合水是未被冻结的吸附水，它与固体间存在某种物理的或化学的作用力，汽化时不但要克服水分子间的作用力，还需克服水分子与固体基质间的结合力。因此，其蒸气压与湿含量有关，且低于纯水的相平衡蒸气压。在一定温度下，吸湿物料的平衡蒸气压与物料湿含量间的关系称为吸附-解吸平衡关系[28-29]

v,eq(,)=(,)0() (9)

其中，0()是Clausius-Clapeyron方程表达的纯组分相平衡的饱和蒸气压[30]

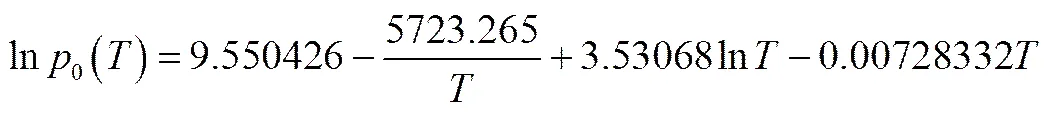
显然，绝干物料的平衡蒸气压为0；最大的平衡蒸气压等于同温度下的相平衡蒸气压，因而其值在0～1之间。本研究采用了幂函数、分式多项式函数和指数函数形式的吸附-解吸平衡关系

(,)=(/0)(11)

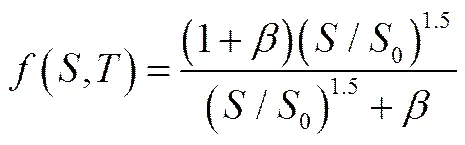
(13)

其中，、和是可调参数。

需要指出的是，本研究并不严格区分升华和解吸，而是将其视为一个过程。因为冰晶和吸附水都是凝聚态湿分，均没有流动性，在所谓的“理想的冷冻干燥过程”中难以区分，且在冰晶升华阶段也有一定量的吸附水发生解吸[1]。

1.5 物性参数

甘露醇为待干料液中的溶质，水为溶剂。为探究具有预制孔隙的初始非饱和多孔物料对冷冻干燥过程的影响，采用初始饱和度0分别为0.28和1.00的两种物料。不同0物料的初始干基湿含量0均为4.48 kg·kg-1。饱和度和湿含量之间的换算关系见文献[15]。物料总质量均为1.8 g，半径=7.4 mm，高度分别为0.28=34.8 mm和1.00=10.7 mm。底盘高度均为5 mm。

渗透率和扩散系数分别为[13,31]

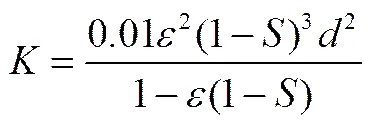
(15)

式中，为待干物料的平均孔径。饱和物料的平均孔径取50 μm[32]，初始饱和度0为0.28物料的平均孔径为77 μm。非饱和物料的平均孔径由初始饱和度的大小计算所得，具体步骤见文献[13]。这两个数值与作者所在课题组的实验观察相吻合[14,16]。其他物性参数见表1。

表1 物理性质

1.6 初始条件和边界条件

物料的初始温度，饱和度和压力均匀分布

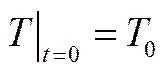
(17)

(18)

在圆柱形物料的对称轴上，无质流及热流

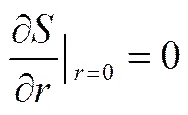
(20)

在物料与底盘的接触面上，无质流

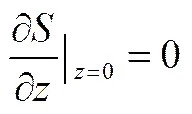
物料组件表面为辐射传热

(22)

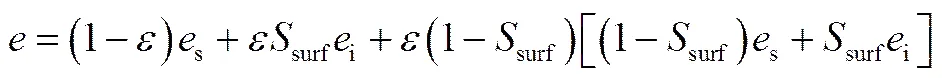
干燥室内压力恒定

(24)

2 数值模拟

本研究使用基于有限元法的多物理场仿真分析平台COMSOL Multiphysics对方程组进行求解。分别选用稀物质传递模块（chds），固体传热模块（ht）和达西流动模块（dl）来进行耦合求解控制方程[式(1)～式(4)以及式(7)]；式(2)中的扩散项是通过修改弱形式的方式添加到Darcy方程中；式(4)中的对流速度是通过增加一个平移运动项将式(3)代入传热方程。材料属性[式(5)、式(6)和式(23)]以及源项[式(8)]均为变量的函数。网格为自由剖分三角形网格，网格单元尺寸选择9级预置单元尺寸中的极端细化，并对网格的疏密程度进行了测试，以保证计算结果与网格数无关。时间离散采用向后差分法，初始步长为10-6s，随后为自由时间步长。相对容差和绝对容差均为10-4s。采用全耦合的MUMPS直接求解器。

3 结果与讨论

3.1 不同0物料的模拟与实验干燥曲线对比

本研究用于对比的实验数据均由作者所在课题组实验测得。实验是在一台自行设计和组装的实验室规模的多功能冷冻干燥装置上进行的，它包括了4个子系统：预冷冻系统，控温系统，真空系统和数据采集系统。实验材料与仪器、装置的工艺流程图以及各个子系统的描述见文献[15-16]。实验中采用“液氮制作冰激凌法”制备初始非饱和多孔物料。有关物料预制孔隙形成过程的描述亦见相同文献。模拟条件均与实验过程的典型操作条件保持一致。表2为实验中的典型操作条件。

表2 典型操作条件

图2和图3分别是吸附-解吸平衡关系为幂函数（=1.1）和分式多项式函数形式（=0.5）下，本研究所得的0为0.28和1.00的物料干燥曲线和实验结果的对比，图中同时包含了Wang等[22]基于局部质量平衡假设的模拟结果。

由图2、图3可知，无论吸附-解吸平衡关系为幂函数还是分式多项式函数形式，与局部质量平衡假设的模拟结果相比较，本研究基于局部质量非平衡假设所得的干燥曲线与实验数据非常吻合，从而验证了模型的可靠性。考察两种物料的干燥过程表明，相比于初始饱和物料，初始非饱和物料的干燥时间明显缩短，确实可以达到强化冷冻干燥的目的。传统液体物料冷冻干燥是将液体直接冷冻，孔隙空间完全被冰晶所占据或饱和，其固有孔径较小。这种物料的干燥机制是表面冰晶先升华，升华后形成的孔隙成为蒸汽向外迁移的通道，因此升华只发生在界面上，升华界面随着干燥过程的进行由外逐渐向内移动。而初始非饱和物料冷冻干燥是先将液体制备成具有预制孔隙的冷冻物料。在冷冻阶段，物料就已形成连续的微观孔道以及相对较大的孔隙空间，并且饱和度越低，孔隙越大，孔壁越纤薄[39]。孔隙越大，传质阻力越小，有利于蒸汽的迁移；孔壁越纤薄，比表面积越大，有利于吸附水的解吸，从而提高了干燥速率。此外，本研究还采用了式(13)的指数函数形式的吸附-解吸平衡关系（=1000）。与以上两个函数形式的平衡关系一样，模拟结果与实验数据也十分吻合。这表明，本研究基于局部质量非平衡假设建立的多孔介质热、质耦合传递模型确实能够准确地再现具有预制孔隙多孔介质冷冻干燥的动力学过程。

事实上，式(12)是Readhead表达多层吸附平衡关系的近似式[40]，式(13)是描述毛细管流动关系的Kelvin方程近似式[41]。这两个方程都属于初等函数。采用3种吸附-解吸平衡关系均获得了优异的模拟结果，说明这些函数具有某种程度上的相似性。数学上，基本初等函数如幂函数、指数函数和三角函数等在一定条件下能够展开成泰勒级数[42]。就这个意义上说，泰勒级数是这些函数的推广，是一种通用的形式。在实际应用中，泰勒级数往往需要截断，只取其前面的有限项。一个函数的有限项的泰勒级数叫做泰勒多项式。因此，吸湿多孔介质的吸附-解吸平衡关系可以统一用泰勒多项式来表达，而不是以往每一种物料需要采用一个特定形式的平衡关系。另外，本模拟尝试忽略传热方程式(4)中的对流项，模拟结果没有改变。这说明对流传热对冷冻干燥的影响可以忽略[6-8,13,17-18,22]。

3.2 典型操作条件下的热、质耦合传递

图4为在典型操作条件下，0=0.28物料内部温度分布。初始温度为冷冻温度−26℃，见图4(a)。干燥初期，物料温度迅速下降到−35℃左右,见图4(b)。这是因为物料内部冰晶发生整体升华，较大的升华速率需要消耗大量的相变潜热，而环境辐射提供的热量不足，因此该阶段所消耗的热量主要来自物料自身的显热，致使物料温度骤降。这与作者所在课题组的实验结果一致[15-16]。支撑底盘由于内部没有相变，吸收辐射能后温度逐渐升高，且总是高于物料的温度。随着干燥过程的进行，物料温度一直缓慢提升，见图4(c)～(e)。直到干燥后期，物料温度才快速升高，上表面升温较快，同时靠近底盘的物料底部温度升高尤其明显，见图4(f)、(g)。这说明除了环境辐射传热外，底盘的导热作用不可忽视，Wang等[22]也得到了相同的结论。干燥结束时，物料温度接近环境温度30℃，见图4(h)。

图5为0=0.28物料内部饱和度分布。初始饱和度均匀分布，见图5(a)。干燥开始时，孔隙中冰晶表面的平衡蒸气压与主流蒸汽压力不平衡，且靠近边缘的传质阻力很小，其饱和度迅速降低，见图5(b)。干燥前期主要去除自由水，径向和轴向的升华强度较大，说明仍然存在较为模糊的升华界面。由于初始非饱和物料孔壁纤薄，比表面积大，湿分主要以吸附水形式存在，因而此阶段较短，见图5(c)、(d)。随着干燥过程的进行，相变产生的蒸汽在压力梯度和浓度梯度作用下，通过预制孔隙可以及时向外迁移，从而促进物料发生整体相变，饱和度逐渐降低，见图5(e)～(g)。物料顶部的干燥速率较大，这是因为初始非饱和物料的高径比较大，干燥过程中侧面的主要传质方向只有径向，而顶部的主要传质方向有径向和轴向两个方向。干燥最慢的区域（冰冻核心）不再是传统饱和物料中出现在物料底部，而是往上靠近物料中心。这是因为初始非饱和物料存在的预制孔隙加之底盘的导热作用，使得物料底部与边缘可以同时发生相变。而传统饱和物料内部没有初始空隙，物料底部中心的冰晶最后升华，这与实验结果一致[14-16]。当物料内部饱和度达到产品要求时，干燥结束，见图5(h)。

与传统饱和物料相比，初始非饱和物料的固有孔隙率增大和初始饱和度减小会降低多孔介质的表面发射率，而且干燥过程中物料底部提前发生相变，增加了传热阻力。因此，与传统饱和物料冷冻干燥过程主要由传质控制相比，初始非饱和物料的干燥过程主要由传热控制。

由于本研究是基于局部质量非平衡假设，而且质量源与饱和度和温度之间有着紧密联系，因此考察干燥过程中质量源的变化十分必要。图6为0=0.28物料内部质量源分布。初始时，孔隙中冰晶和蒸汽的热力学状态偏离平衡态的程度最大，因此传质驱动力最大，相变强度也最大。物料边缘的传质阻力小，因此边缘比物料内部的质量源略大，见图6(a)。干燥初期，由于物料温度骤降，平衡蒸气压迅速降低，传质驱动力减小，相变强度也变小。边缘和底部的质量源较大，这与此处较低的饱和度和较高的温度相互对应。物料顶部，侧面和底部的温度较高，平衡蒸气压较大，因而传质驱动力大，加上预制孔隙的存在，可以使升华/解吸的蒸汽及时逸出，所以这些区域的质量源相对较大，见图6(b)～(d)。随着干燥过程的进行，物料整体相变的现象逐渐显著，干燥速率逐渐降低，质量源维持一个较低的水平，见图6(e)～(g)。这说明，整个物料已经进入到冷冻干燥的次要阶段（secondary stage）。因此，这一阶段需要输入额外的热量以促进结合水的解吸。干燥结束时，物料内的质量源趋近于0，见图6(h)。

以往研究假定，升华只发生在界面上，该界面将整个物料划分为冰冻区和干区。无论对于饱和物料还是非饱和物料，人为的升华界面随着干燥过程的进行由物料表面逐渐向内部移动，在这两个区域中分别有不同的控制方程组[7-8,17,21]。本研究结果表明，升华界面可以自然形成，不需要人为添加移动界面，也不存在严格的冰冻区和干区，物料内任意一点处的热力学状态只要偏离平衡状态就会发生相变，整个物料只用一组控制方程即可。

3.3 辐射温度对冷冻干燥过程的影响

干燥室温度是冷冻干燥过程的重要操作条件。选择适宜的操作温度是改善过程的简单而有效的方法。实验研究已经表明，适当提高操作温度可以明显缩短干燥时间，而操作压力在11～33 Pa范围内对过程的影响甚微[14,16,39]。因此，本研究仅模拟辐射温度对过程的影响，以考察所建模型的预测能力。图7和图8分别为0为0.28和1.00两种物料在不同辐射温度条件下，模型预测的干燥曲线与实验数据的对比。可见，模型预测的干燥时间与实际干燥时间一致，再次验证了模型的有效性。当环境温度较高（30和35℃）时，干燥速率和实验过程的干燥速率非常吻合，当环境温度较低（25℃）时，预测的干燥速率在干燥的前半阶段略低，后半阶段略高于实际干燥速率；干燥结束时，干燥时间与实验结果吻合。这可能是由于模型中多孔物料的有效热导率只是饱和度的函数，没有考虑温度的影响。显然，初始非饱和与常规饱和两种冷冻物料的干燥时间均随辐射温度的升高而缩短。这是因为当环境温度升高时，物料吸收的辐射能增加，有利于干燥过程。由吸附方程可知，温度升高，平衡蒸气压随之增大，传质驱动力变大，因而物料的干燥速率增大。显然，适当地提高干燥室温度是强化冷冻干燥过程的有效途径，但过高的温度会造成冷冻物料在干燥过程中塌陷。需要再次说明的是，3种平衡关系在预测辐射温度影响时，均使用了与典型操作条件下相同的、和值。由此可见，本研究所建模型具有良好的预测能力。

4 结 论

（1）基于质量非平衡假设，建立了多孔介质冷冻干燥热、质耦合多相传递数学模型。模拟结果与实验数据十分吻合，验证了模型的准确性。

（2）在物料量和湿含量均相同的条件下，具有预制孔隙的初始非饱和物料比常规饱和物料的干燥时间明显缩短，理论验证了初始非饱和物料确实可以强化冷冻干燥过程。

（3）考察饱和度、温度和质量源分布表明，干燥过程中，初始非饱和物料内部确实发生了整体相变，过程的主要速率控制因素是传热。

（4）所建模型具有良好的预测能力，提高环境辐射温度对两种物料的冷冻干燥过程均有利，干燥时间均随辐射温度的升高而缩短。

符 号 说 明

c——比热容，J·kg-1·K-1 DK——Knudsen扩散系数，m2·s−1 e——发射率 DH——相变潜热，J·kg−1 K——渗透率，m2 Kr——冰晶升华速率系数，s−1 ——升华源项，kg·m−3·s−1 mw——水的摩尔质量，kg·mol−1 p——压力，Pa Rg——气体常数，J·mol−1·K−1 r——径向空间坐标，mm S——饱和度 T——温度，K t——时间，s X——干基湿含量，kg·kg −1 z——轴向空间坐标，mm ε——固有孔隙率 λ——热导率，J·m−1·s−1·K−1 μ——动力黏度，kg·m−1·s−1 ρ——密度，kg·m−3 σ——斯蒂芬-玻耳兹曼常数，W·m−2·K−4 τ——迂曲度 下角标 amb——环境 b——支撑底盘 i——冰 s——固体基质 surf——表面 v——蒸汽 0——初始

References

[1] LIAPIS A I, BRUTTINI R. Freeze Drying[M]// MUJUMDAR A S. Handbook of Industrial Drying. New York: Marcel Dekker, 2014: 259-1282.

[2] MILLMAN M J, LIAPIS A I, MARCHELLO J M. An analysis of the lyophilization process using a sorption-sublimation model and various operational policies[J]. AIChE Journal, 1985, 31(10): 1594-1604.

[3] MARQUES L G, FREIRE J T. Analysis of freeze-drying of tropical fruits[J]. Drying Technol.2005, 23(9): 2169-2184.

[4] HEDOUX A. Recent developments in the Raman and infrared investigations of amorphous pharmaceuticals and protein formulations: a review[J]. Adv. Drug Deliv. Rev., 2015, 4250(6): 164-170.

[5] RATTI C. Hot air and freeze-drying of high value foods: a review[J]. J. Food Eng., 2001, 49(4): 311-319.

[6] WANG W, CHEN M, CHEN G H. Issues in freeze drying of aqueous solutions[J]. Chin. J. Chem. Eng., 2012, 20(3): 551-559.

[7] 王朝晖, 施明恒. 加热方式对真空冷冻干燥过程的影响[J]. 工程热物理学报, 1997, 18(3): 336-341. WANG Z H, SHI M H. Freeze drying characteristics in different heating methods[J]. J. Eng. Therm., 1997, 18(3): 336-341.

[8] WANG W, CHEN G H. Freeze drying with dielectric- material-assisted microwave heating[J]. AIChE Journal, 2007, 53(12): 3077-3088.

[9] PIKAL M J, ROY M L, SHAH S. Mass and heat transfer in vial freeze-drying of pharmaceuticals: role of the vial[J]. J. Pharm. Sci., 1984, 73(9): 1224-1237.

[10] PIKAL M J. Use of laboratory data in freeze drying process design: heat and mass transfer coefficients and the computer simulation of freeze drying[J]. J. Parenter. Sci. Technol., 1985, 39(3): 115-139.

[11] NAIL S, GATLIN L. Freeze drying: principle and practice[M]// AVIS A, LIEBERMANN A, LACHANN L. Pharmaceutical Dosage Forms. New York: Marcel Dekker, 1993: 163-333.

[12] CHENG X F, ZHANG M, ADHIKARI B. Effect of ultrasonically induced nucleation on the drying kinetics and physical properties of freeze-dried strawberry[J]. Drying Technol.2014, 32(15): 1857-1864.

[13] CHEN M, WANG W, PAN Y Q,. 1D and 2D numerical verification on freeze drying of initially porous material frozen from aqueous solution[C]// CHEN X D, MUJUMDAR A S. Proc. 18th Intern. Drying Symp. (IDS2012). Xiamen, China: XMU, 2012.

[14] WANG W, HU D P, PAN Y Q,. Freeze-drying of aqueous solution frozen with prebuilt pores[J]. AIChE Journal, 2015, 61(6): 2048-2057.

[15] 于凯, 王维, 潘艳秋, 等. 初始非饱和多孔物料对冷冻干燥过程的影响[J]. 化工学报, 2013, 64(9): 3110-3116. YU K, WANG W, PAN Y Q,. Effect of initially unsaturated porous frozen material on freeze-drying[J]. CIESC Journal, 2013, 64(9): 3110-3116.

[16] 赵延强, 王维, 潘艳秋, 等. 具有初始孔隙的多孔物料冷冻干燥[J]. 化工学报, 2015, 66(2): 504-511. ZHAO Y Q, WANG W, PAN Y Q,. Freeze-drying of porous frozen material with initial porosity[J]. CIESC Journal, 2015, 66(2): 504-511.

[17] WANG W, CHEN G H. Heat and mass transfer model of dielectric-material-assisted microwave freeze-drying of skim milk with hygroscopic effect[J]. Chem. Eng. Sci., 2005, 60(23): 6542-6550.

[18] NAM J H, SONG C S. Numerical simulation of conjugate heat and mass transfer during multi-dimensional freeze drying of slab-shaped food products[J]. Int. J. Heat Mass Transf., 2007, 50(23/24): 4891-4900.

[19] HALDER A, DHALL A, DATTA A K. Modeling transport in porous media with phase change: applications to food processing[J]. J. Heat Transf.-Trans. ASME, 2011, 133(3): No.031010.

[20] RATTI C, CRAPISTE G H, ROTSTEIN E. A new water sorption equilibrium expression for solid foods based on thermodynamic considerations[J]. J. Food Sci., 1989, 54(3): 738-742.

[21] LIAPIS A I, BRUTTINI R. A theory for the primary and secondary drying stages of the freeze-drying of pharmaceutical crystalline and amorphous solutes: comparison between experimental data and theory[J]. Sep. Technol., 1994, 4(3): 144-155.

[22] WANG W, HU D P, PAN Y Q,. Numerical investigation on freeze-drying of aqueous material frozen with pre-built pores[J]. Chin. J. Chem. Eng., 2016, 24(1): 116-125.

[23] SCARPA F, MILANO G. The role of adsorption and phase change phenomena in the thermophysical characterization of moist porous materials[J]. Int. J. Thermophys., 2002, 23(4): 1033-1046.

[24] SHEEHAN P, LIAPIS A I. Modeling of the primary and secondary drying stages of the freeze drying of pharmaceutical products in vials: numerical results obtained from the solution of a dynamic and spatially multi-dimensional lyophilization model for different operational policies[J]. Biotechnol. Bioeng., 1998, 60(6): 712-728.

[25] Whitaker S. Simultaneous heat, mass, momentum transfer in porous media: a theory of drying[J]. Adv. Heat Transf., 1977, 13(8): 119-203.

[26] HALDER A, DHALL A, DATTA A K. An improved, easily implementable, porous media based model for deep-fat frying (Ⅰ): Model development and input parameters[J]. Food Bioprod. Process., 2007, 85(3): 209-219.

[27] WARNING A, ARQUIZA J M R, DATTA A K. A multiphase porous medium transport model with distributed sublimation front to simulate vacuum freeze drying[J]. Food Bioprod. Process., 2015, 94(1): 637-648.

[28] WOLFF E, GIBERT H, RODOLPHE F. Vacuum freeze-drying kinetics and modeling of a liquid in a vial[J]. Chem. Eng. Process., 1989, 25(3): 153-158.

[29] WANG W, CHEN G H. Physical interpretation of solid drying: an overview on mathematical modeling research[J]. Drying Technol., 2007, 25(4): 659-668.

[30] MURPHY D M, KOOP T. Review of the vapour pressures of ice and supercooled water for atmospheric applications[J]. Q. J. R. Meteorol. Soc., 2005, 131(608): 1539-1565.

[31] GEANKOPLIS C J. Transport Processes and Unit Operations[M]. New Jersey: Englewood Cliffs, 1993: 462-468.

[32] NAKAGAWA K, HOTTOT A, VESSOT S,. Modeling of freezing steps during freeze-drying of drugs in vials[J]. AICHE Journal, 2007, 53(5): 1362-1372.

[33] PERRY H R, GREEN D W, MALONEY J O. Perry’s Chemical Engineers’ Handbook[M]. New York: McGraw-Hill, 1997: 2-337.

[34] ECKERT E R G, DRAKE R M. Thermophysical Properties, Analysis of Heat and Mass Transfer[M]. New York: McGraw-Hill, 1987: 767-783.

[35] LILEY P E. Physical and chemical data[M]// PERRY H R, GREEN D W, MALONEY J O. Perry’s Chemical Engineers’ Handbook. New York: McGraw-Hill, 1997, 2: 40-304.

[36] BIRD R B, STEWART W E, LIGHTFOOT E N. Transport Phenomena[M]. New York: John Willey and Sons, 2002: 488-508.

[37] IDELCHIK I E. General Information and Element of Aerodynamics and Hydraulic of Pressure Systems[M]// STEINBERG M O, MALYAVSKAYA G R, MARTYNENKO O G. Handbook of Hydraulic Resistance. Florida: CRC Press, 1994: 9-12.

[38] LIDE D R. Handbook of Data on Organic Compounds[M]. Florida: CRC Press, 1994: 3338.

[39] 李恒乐, 王维, 李强强, 等. 具有预制孔隙多孔物料的冷冻干燥[J]. 化工学报, 2016, 67(7): 2857-2863. LI H L, WANG W, LI Q Q,. Freeze-drying of porous frozen material with prefabricated porosity[J]. CIESC Journal, 2016, 67(7): 2857-2863.

[40] DO D D. Pure Component Adsorption in Microporous Solids, Adsorption Analysis: Equilibria and Kinetics, Series on Chemical Engineering[M]. London: Imperial College Press, 1998:188-190.

[41] RAJNIAK P, YANG R T. Unified network model for diffusion of condensable vapors in porous media[J]. AIChE Journal, 1996, 42(2): 319-331.

[42] EDMONTON B. Brook Taylor[M]// GOWERS T, BARROW- GREEN J, LEADER I. The Princeton Companion to Mathematics. Princeton: Princeton University Press, 2008: 745-745.

Multiphase transport model for freeze-drying of porous media with prefabricated porosity

NIU Lijiao1, WANG Wei1, PAN Siqi2, ZHANG Dawei1, CHEN Guohua3

(1School of Chemical Machinery and Safety, Dalian University of Technology, Dalian 116024, Liaoning, China;2School of Environmental and Chemical Engineering, Dalian University, Dalian 116622, Liaoning, China;3Department of Chemical and Biomolecular Engineering, The Hong Kong University of Science and Technology, Hong Kong, China)

Based on the hypothesis of the local mass non-equilibrium, a multiphase porous media drying model of heat and mass transfer was developed to verify the effect of porous frozen materials with prefabricated porosity on freeze-drying. Three kinds of adsorption-desorption equilibrium relationships were constructed to express the hygroscopic effect of moist porous media. The model was solved numerically on the commercial software platform of COMSOL Multiphysics based on the finite element method. Results showed that the freeze-drying process can be effectively enhanced with the initially unsaturated material. Excellent agreements were achieved between model simulative results and experimental data using the three kinds of the proposed adsorption-desorption equilibrium relationships. The different relationships can be unified into a Taylor polynomial through Taylor extensions of some elementary functions. Heat and mass transfer mechanism was discussed according to temperature, saturation and mass source profiles. The drying rate-controlling factor is mainly heat transfer for the initially unsaturated material. Numerical examination of the ambient temperature effect on the freeze-drying process illustrated that the developed model provided good prediction capacities.

freeze-drying; unsaturated porous media; local mass non-equilibrium; adsorption-desorption equilibrium; heat and mass transfer

10.11949/j.issn.0438-1157.20161289

TQ 028.5; TQ 026.6

A

0438—1157（2017）05—1833—12

王维。

牛利娇（1990—），女，硕士研究生。

国家自然科学基金项目（21676042）；辽宁省自然科学基金项目（201602167）；中央高校基本科研业务费专项资金项目（DUT14RC(3)008）。

2016-09-13收到初稿，2017-01-17收到修改稿。

2016-09-13.

WANG Wei, dwwang@dlut.edu.cn

supported by the National Natural Science Foundation of China (21676042), the Natural Science Foundation of Liaoning Province (201602167) and the Fundamental Research Funds for the Central Universities of China (DUT14RC(3)008).