基于非参数核密度估计与数值天气预报的风速预测修正方法

刘晓楠 ，周介圭 ，2，贾宏杰 ，穆云飞 ，王 彤 ，戴晨松

（1.天津大学 智能电网教育部重点实验室，天津 300072；2.铁道第三勘察设计院集团有限公司电化电信处，天津 300251；3.南京南瑞太阳能科技有限公司，江苏 南京 211106）

0 引言

风能作为一种蕴藏量大、清洁、分布区域广的重要可再生能源，日益受到各国的广泛关注。风力发电作为目前成本较低、技术最为成熟的可再生能源利用形式，具备大规模开发及商业化利用的发展前景。然而与常规能源发电不同，受制于风速的间歇性及波动性的特点，风电难以为系统所调度，当风电穿透功率较高时（一般大于8%），可能会严重影响电力系统的发电计划、调度、潮流分布、电压及频率的稳定、继电保护装置的设定、电力市场电价制定等多方面［1-4］。因此，风速及风电功率的精确预测变得尤为重要。当前对于风速预测方法的研究主要分为物理方法与统计方法两大类。

物理方法主要考虑一些物理量，如天气数据（风速、风向、气压等）、风电场周围的信息（等高线、粗糙度、障碍物等）以及风电机组的技术参数（轮毂高、穿透系数等）。其目的是找到风电机组轮毂高度处的风速最优估计值，然后使用模型输出统计MOS（Model Output Statistic）以减小预测误差，最后根据风电场的功率曲线计算得到风电场的输出功率［5］。文献［6-7］在考虑了粗糙度变化、地形变化和尾流效应的基础上对风速进行了预测和修正，进而计算得到风电场的输出功率。然而，通过物理方法对风速进行预测的计算量大，且对信息量要求较高，风电场一般难以完整提供相应数据。

统计方法则在对历史数据进行概率学分析的基础上，对未来一段时间内气象数据（风速、风向、气压等）进行预测，从而转换为风电场输出功率。常用的统计模型主要包括时间序列模型、人工神经网络（ANN）及支持向量机（SVM）［8］等方法。文献［9-10］采用神经网络方法对风速进行了预测；文献［11］将时间序列分析和卡尔曼滤波法相结合对风电功率进行预测；文献［12］综合了持续法、时序差分自回归滑动平均法和自适应模糊神经网络法3种方法的优点，通过模糊判断矩阵方法进行预测；文献［13］介绍了风速预测的支持向量机模型，分别利用支持向量机与多层感知器神经网络对风速进行了预测，并对预测结果进行了对比分析。然而，在上述统计预测方法中，风速预测所产生的相位误差依旧无法避免。

针对上述问题，本文提出了一种基于非参数核密度估计和数值天气预报NWP（Numerical Weather Prediction）的风速预测修正方法。首先，利用非参数核密度估计法对风速初始预测结果的误差进行估计，并修正初始预测方法所产生的误差，该方法在误差估计时并不添加任何的人为假设环节，仅从数据本身出发寻找误差规律，可以看作一种误差自修正的过程；随后，引入NWP对预测结果进行精确修正，有效提高了风速的预测精度。

1 非参数核密度估计风速修正模型

1.1 非参数核密度估计基本原理

考虑一个平稳的风速偏差时间序列，如式（1）所示，并假设其在时间间隔t=1，2，…，n内已知，且符合马尔可夫模型式（2）［14］。

其中，Yt∈R 为响应变量；Xt∈Rk为 k 维解释性向量，由式（1）中的一些样本所构成；m（·）为未知的自回归函数；εt为随机干扰项。

基于数据驱动的非参数核密度估计既不对m（Xt）的函数形式做任何假定，也不人为设置任何参数，完全由数据决定函数在每一点Xt的值。本文使用常用的N-W（Nadaraya-Watson）核估计方法实现对m（·）的估计，它利用预测出的时序变化风速数据与实际风速数据之差，即预测误差之间所具有的强相关性来进行误差预测。

设表示k个连续风速偏差所构成的向量变量，若已知风速偏差向量Xk的n个样本，则 Xk的联合概率密度函数f（Xk）的核密度估计可以定义为式（3）［14］。

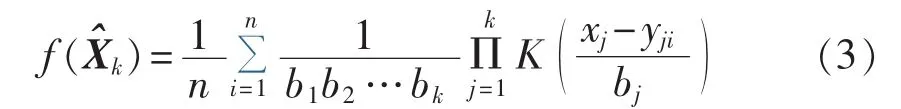
其中，K（·）为核函数或（窗函数）；bj为第j个风速偏差变量的平滑系数（带宽或窗宽），表征了核函数在偏差样本点附近的作用范围。通常，均匀、三角、高斯、余弦函数等均可作为核函数。由于当平滑系数b为最优选择时，不同的核函数一般都能够使得核密度估计具有稳定相合性［14］。因此，本文采用标准高斯核函数。

式（3）为k个连续时序风速偏差的联合概率密度分布，在预测风速偏差时，通常利用前k-1个时刻的已知风速预测偏差值Xk-1=[x1，x2，…，xk-1]T来预测下一时刻k的风速预测偏差值Xk。当选取高斯核函数为 K（x）=（2π）-1/2exp（-x2/2）时，m（·）的非参数N-W 核估计的表达式如（4）所示。

在利用非参数核密度估计预测风速偏差时，需要确定维数k与带宽b，确定的方法有多种，主要包括交叉验证法［15］与最终预测误差法［16］等，本文利用最终预测误差法确定维数k，并通过交叉验证法确定最优带宽 b［14］。

1.2 序列平稳化检验与平稳化

非参数核密度估计的计算要求样本为平稳序列，故需要首先对风速偏差数据进行平稳化检验，然后再对非平稳序列进行平稳化处理。

本文利用一种高效非参数检验方法——随机游程检验来进行风速偏差样本的平稳化检验［17］。假设一个由0和1构成的序列的游程个数为R，拒绝域的临界值为 c1和 c2。当｛R≤c1｝∪｛R≥c2｝（c1＜c2）时，应拒绝原平稳性假设；当c1＜R＜c2时，则无法拒绝平稳性假设，可认为观察值序列是平稳的［7］。当样本容量很大时，c1与 c2可分别由式（5）、（6）确定。

其中，M为数字0出现的个数；N为数字1出现的个数；Zα/2为显著性水平为α时的正态分布值。

本文中需要进行检测的是风速预测偏差序列，并非二元数据，此时可以采用中位数法［17］，将风速预测偏差序列进行二元化转换。此处取中位数xmed为样本均值，即所有风速偏差的平均值，令：

其中，s=1，2，…，k；i=1，2，…，n。序列中比 xmed小的观察值记为 0，不小于 xmed的观察值记为 1。记 X′k，i=［y′1i，y′2i，…，y′ki］T，此时则将检验 Xk，1、…、Xk，n的平稳性问题转化为X′k，1、…、X′k，n的平稳性检验问题。

如果经检验序列为非平稳序列，则需循环执行差分法来平稳化序列［18］，直至序列通过平稳性检验为止。

1.3 风速误差指标与改进

评估预测效果需要适当的评价指标。常用的误差评价指标有平均绝对误差MAE（Mean Absolute Error）、均方根误差 RMSE（Root Mean Square Error）等［19］。在风速预测中，只使用一种误差评价指标无法全面地评估预测效果的优劣。本文采用平均绝对误差、均方根误差、平均绝对百分比误差MAPE（Mean Absolute Percentage Error）3种预测误差指标来共同对预测效果进行衡量［20］。3种误差指标的计算表达式如下：

其中，′k和 x′k分别为预测风速值与实际风速值；p 为预测风速的个数。

由于实际中可能出现风速为0或接近于0的情况，因此当使用E3时，即使很小的预测偏差也可能导致误差指标接近于无穷大；而在风速较大时，即使较大的预测偏差，误差指标也会很小，从而导致不能客观反映预测精度。为克服E3的这一局限性，引入历史最大风速 x′max，将 E3中的实际风速值 x′k用 x′max代替，并用E′3表示修正后的E3，此时的表达式如下：

1.4 基于非参数核密度估计的风速偏差修正步骤

本文使用Chebyshev神经网络预测风速后［21］，利用非参数核密度估计对风速预测偏差进行修正，具体步骤如下。

a.利用神经网络对r天每小时风速进行预测，得到24×r个风速预测点。

b.利用r-l（l为进行风速预测的天数）天的实际风速值与神经网络所预测风速之差，来获得风速预测偏差值，得到由24×（r-l）个风速偏差值构成的风速预测偏差序列。

c.对此风速预测偏差序列进行平稳性检验，若为非平稳序列，则将按1.2节所述方法转换为平稳化序列。

d.利用最终预测误差法确定非参数核密度估计样本维数k。

e.利用此风速预测偏差序列，建立用于非参数核密度估计以进行l天内风速预测偏差修正的样本Xk，i（i=1，2，…，n），建立方法如图1 所示，风速偏差数据样本个数为 n=24×（r-l）-（k-1）。

图1 样本建立方法Fig.1 Establishment method of sample

f.通过交叉验证法确定最优带宽b。

g.对自回归函数进行N-W核密度估计，以得到偏差估计值（x）。

h.利用（x）对预测时刻风速偏差值进行非参数预测。

i.对风速偏差预测值按照式（8）、（9）、（11）所示的指标进行误差分析。

非参数核密度估计方法可以在对样本总体分布形式未知且无需做任何假设的情况下，仅从样本本身出发研究数据的分布特征。但是非参数核密度估计方法属于统计方法的范畴，预测结果会存在相位误差的问题。当风速出现突变拐点时，该方法预测出的位于拐点下一小时时刻的风速偏差可能会与实际风速偏差方向相反，从而产生“误修正”问题（如3.1节中算例所示），使得修正后风速预测效果反而变差。为解决上述问题，本文引入NWP来精确预判风速突变拐点的发生时刻，避免在这些突变拐点下一点所进行的“误修正”，以有效改善风速预测精度。

2 基于非参数核密度估计与NWP的风速预测修正方法

NWP以客观气象数据为基础，通过建立数值预报模式，在一定的初值及边界条件下，通过数值计算预测未来天气。在此过程中通过处理大量的观测数据并求解大气动力学方程组，有效缓解了单纯从历史风速出发进行逐点预测的相位滞后性问题。本文引入NWP，以提前判断风速突变拐点的到来时刻。天气研究与预报模式WRF（Weather Research and Forecasting Model）是新一代的中尺度数值天气预测系统，专为天气业务预报和大气研究而设计［22］，本文将基于WRF天气预报数据开展研究。

结合非参数核密度估计法与WRF对初始预测风速进行综合修正的流程图如图2所示。

图2 初始风速预测及修正流程图Fig.2 Flowchart of initial wind speed prediction and error correction

3 算例分析

以某测风塔2011年4月1日至7月18日间实测风速为测试数据，首先建立风速预测的Chebyshev神经网络模型，并利用2011年4月1日至5月11日每小时风速值训练网络，预测出5月12日至7月18日每小时风速值。然后建立偏差预测的非参数核密度估计模型，通过5月12日至7月15日的预测风速与实测风速的比较，得到其对应的预测偏差，从而建立估计样本 Xk，i= ［y1i，y2i，…，yki］T（i=1，2，…，n），Xk，i为目标时间点前2 h与目标时间点的风速预测偏差，即k=3，修正对象为7月16日至7月18日每小时风速值（共72 h）。

3.1 应用非参数核密度估计方法修正风速预测偏差

为说明非参数核密度估计方法修正初始预测风速的特点，图3给出该方法风速偏差修正效果及其与Chebyshev神经网络预测方法结果的对比效果。

图3 72 h风速预测偏差修正效果图Fig.3 Correction effect of wind speed prediction error in 72 hours

由图3可知，非参数核密度估计法对风速偏差的修正效果可以从2个方面说明：第一，在风速持续单调变化且风速趋于线性变化阶段，包括风速持续平稳上升、平稳下降和风速变化微小时，此方法对于风速预测偏差的修正效果较为明显，如风速持续平稳下降的第2—5 h、风速持续平稳下降的第35—38h以及风速变化微小的第50—53 h等；第二，在风速变化趋势不平稳阶段，尤其是风速曲线突变拐点的下一时刻，如第25、27、33、37 h 等，出现“误修正”问题，修正后的预测结果很不理想，极大地影响了整体修正效果，甚至使得整体误差评价指标劣于修正前，产生这个问题的根源是单纯利用数值进行预测的普遍缺陷，即相位的滞后性。

从表1中可以看出，使用非参数核密度估计方法修正初始预测风速后，风速预测的整体预测误差指标由于某些点预测误差变大反而变得更差。然而非参数核密度估计方法能够在某些风速变化阶段有效改善初始预测结果，本文充分利用这些阶段开展基于非参数核密度估计方法的修正，进而寻求规避产生误差增大因素的方法。由第2节分析可知，导致风速预测效果变差的原因是风速在某一时刻变化趋势发生突变，即风速由上升变为下降或反之。如果能够提前判断出这些突变拐点，则可充分利用非参数核密度估计方法的修正能力，下节将通过NWP来改善初始风速预测效果。

3.2 NWP的风速预测效果

图4给出测试样本中2011年7月13日至7月15日时间段的每小时实际风速值共72 h的WRF NWP开展风速预测值。可以看出，NWP对于风速的预测效果并不十分理想，但是在此处若不考虑风速预测的数值偏差，只关注于风速突变拐点的相位预测效果，NWP则具有较好的预测效果。由于实际预测中事先是无法知道实际风速的，所以在预测时无法判断NWP数据对风速拐点预测的正确性，以下利用测试样本中2011年7月13日至7月15日时间段的每小时实际风速值和对应时间的NWP风速预测值进行对比，来说明利用NWP数据在一定程度上可以对实际风速的突变拐点做出有效预测。如图5为在测试样本中得到预测的72 h中，实际风速出现突变拐点的时间点与NWP风速出现突变拐点的时间点对照图，若预测时刻为风速突变拐点，则用数值1表示，反之用数值0表示。

图4 72 h的风速数值天气预报Fig.4 NWP of wind speed in 72 hours

图5 风速突变拐点对照图Fig.5 Comparison of wind speed inflection points

由图5可以看出，实际风速共出现25个突变拐点，NWP风速共出现35个突变拐点。其中NWP成功预测出21个突变拐点，即在这21个点的下一时刻点，若不采用其进行风速修正，则非参数核密度估计方法会做出不理想的修正，而导致误差增大。还有4个实际突变拐点没有被预测出，在这4个点的下一时刻，虽然非参数核密度估计方法做出了不理想的修正，但是修正值仍然被采用了。有14个NWP突变拐点为错误预测，即在这14个点的下一时刻点，即使非参数核密度估计方法能够有效修正初始预测值，也无法被采用，虽然在这14个点预测是错误的，但并不会产生负面的预测效果。

通过上述分析可以看出，NWP在一定程度上可以对实际风速的突变拐点做出有效预测。因此，在利用Chebyshev神经网络得到的风速预测值的基础上，再通过NWP预测结果找出突变拐点，这些点的值可直接利用Chebyshev神经网络预测的值作为最终的风速预测值，剩余的点则需要利用非参数估计法进行修正。

对于在此需要预测的7月16日至7月18日的72 h而言，根据NWP预测出了38个风速拐点，这38个点不做修正，直接使用初始预测值作为最终的风速预测值，剩下的34个点使用非参数核密度估计法进行修正。

3.3 非参数核密度估计法与NWP相结合的风速偏差修正

根据上述分析，现应用Chebyshev神经网络、非参数核密度估计方法、非参数核密度估计与NWP相结合方法（综合修正方法）对7月16日至7月18日风速进行预测和修正，最终效果如图6所示。

图6 72 h风速预测及修正结果Fig.6 Results of wind speed prediction and error correction in 72 hours

采用不同预测方法修正前、后风速预测误差如表1所示。

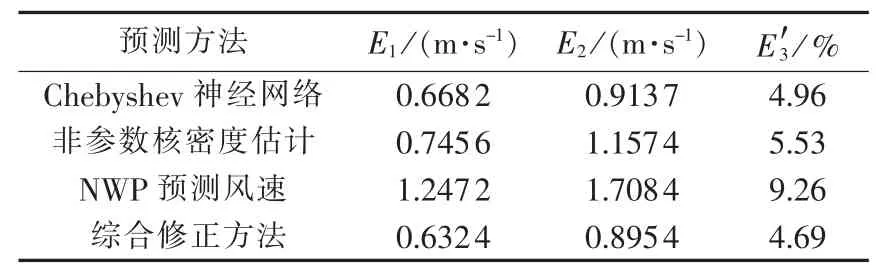
表1 修正前后风速预测误差Table 1 Wind speed prediction errors before and after correction

通过图6和表1可以看出，使用本文提出的综合修正方法可以在相当一部分预测点对神经网络的预测结果进行修正，3类误差指标都有所改善。在此方法中，NWP起到了重要的作用，在最终的结果中，一部分风速突变拐点由于NWP的不准确没有被判断出来，导致不理想的修正被错误采用；还有一部分非突变拐点被NWP误判，导致理想修正没有被利用，这些都影响了最终的修正效果。如何提高NWP的拐点预测能力，是今后研究的重点。

4 结论

本文给出了一种基于非参数核密度估计与NWP的风速预测修正方法。首先利用非参数核密度估计建立风速预测初始预测偏差的模型；随后结合NWP建立风速综合修正模型，通过预判风速突变拐点，然后利用非参数核密度估计方法中理想的修正点，避免风速突变拐点处的“误修正”问题，以达到良好的预测修正效果。最后通过对实际风速的预测验证了此方法的有效性。

同时，由分析可知，NWP的预测精度对风速预测修正效果起着至关重要的作用，NWP对风速突变拐点的错误预测直接会导致综合修正方法在某些预测点的失效，甚至导致预测误差增大。因此，提高NWP的预测精度对于提高最终的修正效果至关重要。此外，如何避免NWP预测误差所导致的预测精度问题，也是下一步开展的研究方向。

参考文献：

［1］雷亚洲.与风电并网相关的研究课题［J］.电力系统自动化，2003，27（8）：84-89.LEI Yazhou.Studies on wind farm integration into power system［J］.Automation of Electric Power Systems，2003，27（8）：84-89.

［2］MU Y F，JIA H J.An approach to determining the local boundaries of voltage stability region with wind farms in power injection space［J］.Sci China Tech Sci，2010，53（12）：3232-3240.

［3］文玉玲，晁勤，吐尔逊依布拉.风电场的继电保护［J］.可再生能源，2009，27（1）：93-96.WEN Yuling，CHAO Qin，TUERXUN Yibula.Study on the relay protection for wind farm［J］.Renewable Energy Resources，2009，27（1）：93-96.

［4］陈树勇，戴慧珠，白晓民，等.风电场的发电可靠性模型及其应用［J］.中国电机工程学报，2000，20（3）：26-29.CHEN Shuyong，DAIHuizhu，BAIXiaomin，etal.Reliability model of wind power plants and its application［J］.Proceedings of the CSEE，2000，20（3）：26-29.

［5］刘烨，卢小芬，方瑞明，等.风力发电系统中风速预测方法综述［J］.电网与清洁能源，2010，26（6）：62-66.LIU Ye，LU Xiaofen，FANG Ruiming，et al.A review on wind speed forecast methods in wind power system［J］.Power System and Clean Energy，2010，26（6）：62-66.

［6］冯双磊，王伟胜，刘纯，等.风电场功率预测物理方法研究［J］.中国电机工程学报，2010，30（2）：1-6.FENG Shuanglei，WANG Weisheng，LIU Chun，et al.Study on the physical approach to wind power prediction［J］.Proceedings of the CSEE，2010，30（2）：1-6.

［7］LANDBERG L.Short-term prediction of the power production from wind farms［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，80：207-200.

［8］张颖超，郭晓杰，叶小岭，等.一种短期风电功率集成预测方法［J］.电力系统保护与控制，2016，44（7）：90-95.ZHANG Yingchao，GUO Xiaojie，YE Xiaoling，etal.Anintegrated forecasting method of short-term wind power［J］.Power System Protection and Control，2016，44（7）：90-95.

［9］张颖超，王雅晨，邓华，等.基于IAFSA-BPNN的短期风电功率预测［J］.电力系统保护与控制，2017，45（7）：58-63.ZHANG Yingchao，WANG Yachen，DENG Hua，etal.IAFSABPNN for wind power probabilistic forecasting［J］.Power System Protection and Control，2017，45（7）：58-63.

［10］陈烨，高亚静，张建成.基于离散Hopfield模式识别样本的GRNN非线性组合短期风速预测模型［J］.电力自动化设备，2015，35（8）：131-136.CHEN Ye，GAO Yajing，ZHANG Jiancheng.GRNN nonlinear combination model for short-term wind speed forecasting based on discrete Hopfield pattern recognition［J］.Electric Power Automation Equipment，2015，35（8）：131-136.

［11］潘迪夫，刘辉，李燕飞.基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型［J］.电网技术，2008，32（7）：82-86.PAN Difu，LIU Hui，LIYanfei.A wind speed forecasting optimization modelforwind farms based on time series analysis and Kalman filter algorithm［J］.Power System Technology，2008，32（7）：82-86.

［12］黄文杰，傅砾，肖盛.采用改进模糊层次分析法的风速预测模型［J］.电网技术，2010，34（7）：164-168.HUANG Wenjie，FU Li，XIAO Sheng.A predictive model of wind speed based on improved fuzzy analytical hierarchy process［J］.Power System Technology，2010，34（7）：164-168.

［13］MOHANDES M A，HALAWANI T O，REHMAN S.Supportvector machines for wind speed prediction［J］.Renewable Energy，2004，29（6）：939-947.

［14］赵渊，张夏菲，谢开贵.非参数自回归方法在短期电力负荷预测中的应用［J］.高电压技术，2011，37（2）：429-435.ZHAO Yuan，ZHANG Xiafei，XIE Kaigui.Application of nonparametric auto-regression to short-term load forecasting［J］.High Voltage Engineering，2011，37（2）：429-435.

［15］HARDLE W，CHEN Rong.Nonparametric time series analysis，a se-lective review with examples［J］.Journal of Nonparametric Sta-tistics，1995（5）：157-184.

［16］TJOSTHEIM D，BAUESTAD B H.Nonparametric identification of nonlinear time series：selecting significant lags［J］.Journal of the American Statistical Association，1994，89（428）：1410-1419.

［17］吴喜之，王兆军.非参数统计方法［M］.北京：高等教育出版社，1996：26-28.

［18］蔡凯，谭伦农，李春林，等.时间序列与神经网络法相结合的短期风速预测［J］.电网技术，2008，32（8）：82-85.CAIKai，TAN Lunnong，LIChunlin，etal.Short-term wind speed forecasting combing time seriesand neuralnetwork method［J］.Power System Technology，2008，32（8）：82-85.

［19］刘立阳，孟绍良，吴军基.风电功率预测技术综述［J］.电力自动化设备，2016，36（9）：87-93.LIULiyang，MENG Shaoliang，WU Junji.Dynamic economic dispatch based on wind powerforecasterror interval［J］.Electric Power Automation Equipment，2016，36（9）：87-93.

［20］谷兴凯，范高锋，王晓蓉，等.风电功率预测技术综述［J］.电网技术，2007，31（增刊 2）：335-338.GU Xingkai，FAN Gaofeng，WANG Xiaorong，et al.Summarization of wind power prediction technology［J］.Power System Technology，2007，31（Supplement 2）：335-338.

［21］邹阿金，张雨浓.基函数神经网络及应用［M］.广州：中山大学出版社，2009：132-151.

［22］王晓君，马浩.新一代中尺度预报模式（WRF）国内应用进展［J］.地球科学进展，2011，26（11）：1191-1199.WANG Xiaojun，MA Hao.Progress of application of the Weather Research and Forecast（WRF） model in China［J］.Advances in Earth Science，2011，26（11）：1191-1199.