应用于直流配电网的双向全桥直流变换器比较分析

孙谦浩 ，王 裕 ，宋 强 ，赵 彪 ，李建国

（1.清华大学 电机系 电力系统及发电设备控制和仿真国家重点实验室，北京 100084；2.华北电力大学 电气与电子工程学院，北京 102206）

0 引言

近年来，直流配电网因其线路造价低、电能损耗小、供电可靠性高、储能和新能源发电系统接入成本低等技术和经济优势逐渐受到人们的关注［1-9］。在直流配电网的发展过程中，直流变换器作为其关键设备得到了学者们的广泛研究［10］。基于高频隔离的双向全桥直流变换器（DAB）因具有电气隔离、能量可双向传输、高功率密度、噪音小、污染小等优点，在直流变压以及双向功率传输等场合的应用中逐渐成为研究热点［11-12］。文献［13-18］分别从拓扑改进、电气特性、电流应力、死区效应、软开关行为、系统损耗与效率分析等方面对非缓冲式DAB进行了深入的探讨和分析。文献［19-21］对电容缓冲式DAB（CBDAB）进行了功率损耗分析、电压波动限制分析、采用不同材料的开关管的影响对比分析及其在航空系统中的应用研究。但上述研究在对电容缓冲式DAB分析中，都忽略了缓冲电容对高频链波形的影响，而且缺少对缓冲式DAB与非缓冲式DAB软开关特性的比较分析，以及缓冲电容对高频环节电压du/dt、变换器传输功率和回流功率的影响分析。

本文首先针对非缓冲式DAB的半软开关特性，对电容缓冲式DAB采用了死区时间移相控制。在实现电容缓冲式DAB的全软开关行为的同时，对非缓冲式DAB应用中高频环节存在较大du/dt的关键问题也具有良好的抑制作用，减小了过大du/dt对高频变压器（HFT）的绝缘危害，拓宽了电容缓冲式DAB在直流配电网，特别是在中高压直流配电网中的适用范围。然后，针对电容缓冲式DAB与非缓冲式DAB，本文详细分析并比较了二者的开关特征，从而得出了缓冲电容对高频环节波形的影响规律。在对比开关特征的基础上，对缓冲电容与du/dt的关系进行了详细的分析，结果表明缓冲电容越大，对高频环节电压du/dt的抑制作用越明显。此外，针对电容缓冲式DAB与非缓冲式DAB的不同开关特征带来的影响，从传输功率与功率因数2个角度分别进行了详细的分析，并且推导出二者传输功率表达式与功率因数表达式的统一形式，得到二者之间的联系与区别。最后，通过仿真与样机实验说明了理论分析的正确性。

1 移相控制与死区移相控制

1.1 非缓冲式DAB与电容缓冲式DAB的拓扑结构

图1（a）给出了非缓冲式DAB变换器与电容缓冲式DAB变换器的拓扑结构。图中，VT1—VT4、V′T1—V′T4分别为 H1桥、H2桥的开关器件；VD1—VD8为与开关器件反并联的二极管。对于非缓冲式DAB，其开关组成图中的S′，只包括开关管及与其反并联的二极管；而对于电容缓冲式DAB，其开关组成图中的S，即以S′为基础，在开关 VT1— VT4、V′T1—V′T4两端分别并联缓冲电容C1—C8（包括开关器件自身寄生电容），从而构成电容缓冲式开关。

1.2 移相控制与死区移相控制

图1（b）与 1（c）分别给出了非缓冲式 DAB移相控制与电容缓冲式DAB死区移相控制的原理图。图中S1—S4、Q1—Q4分别为开关管VT1—VT4、V′T1—V′T4的驱动脉冲信号，D为H1桥与H2桥的移相比，M为死区系数，K为电容缓冲系数。从图中可以看出，在非缓冲式DAB中采用移相控制下，各个开关的触发脉冲是占空比为50%的方波，而死区移相控制下的开关管脉冲由于死区时间的存在，并不是方波。通过设定合理的死区时间，以满足电容缓冲式DAB中缓冲电容的能量交换，便可以提高变换器的运行性能与效率（死区时间设定条件将在下文3.1节中进行分析）。

图1 非缓冲DAB与CBDAB拓扑结构及控制原理Fig.1 Topological structure and control principle of CBDAB and DAB without buffer

2 电容缓冲式DAB与非缓冲式DAB开关特性比较

由于DAB类变换器在运行过程中的对称性，因此本文以半个开关周期为例，对电容缓冲式DAB与非缓冲式DAB的开关特性进行分析与比较。假设变换器已经达到了稳态运行，而且电感足够大，能够维持死区时间内的电感电流不变向，那么分别对图1（b）与图1（c）进行分析，可以得到二者的开关特性如下。

2.1 电容缓冲式DAB开关特性与高频环节波形特征分析

a.t0—t′0阶段。t0前，H1桥开关管 VT2、VT3导通，H2桥开关管 V′T2、V′T3的续流二极管 VD6、VD7导通。t0时，VT2、VT3关断，由于死区时间的存在，VT1、VT4并未导通；由于缓冲电容C2、C3的电容电压保持为0，因此，开关管VT2、VT3实现了零电压关断。当VT2、VT3关断后，由于缓冲电容 C1、C4的箝位作用，VT1、VT2的续流二极管VD1、VD2不能导通，此时，电感电流只能强制对电容 C1、C4放电，对电容 C2、C3充电。H1桥中的电感电流流经2条通路，分别为：流经C1、C3，对C1进行放电，对 C3进行充电；流经 C2、C4，对 C4进行放电，对C2进行充电。假设缓冲电容的参数完全相同，电容值都为C，则流经每一通路的电流为iL/2。此时，电路方程可表示为：

式（1）为二阶方程，由初始条件 uC1（0）=U1，uC3（0）=0，iL（0）=-I0，可得：

其中，ω0为谐振频率；Z0为谐振阻抗；θ0、k 为由初始条件决定的参数。

由式（2）可知，t0— t′0阶段中电感电流为正弦变化，缓冲电容电压与高频变压器的高频链电压uh1均为余弦变化。这与非缓冲式DAB方波调制中的垂直上升不同，可以明显减小uh1的du/dt变小，避免其对高频变压器带来的绝缘损害。

b.t′0— t1阶段。t′0时，电容 C1、C4上的电荷分别全部转移到电容 C2、C3上，uC1、uC4变为 0，uC2、uC3变为U1。由于电感足够大，电感电流并没有反向，只是相比t0时的电流略微有所减小，因此，续流二极管VD1、VD4导通，uh1变为U1。这个过程中，由于电流反向，左侧在吸收功率，电感将能量返送到左侧电源，这部分功率称为回流功率。该过程中，电感两端电压与电感电流可以表示为：

c.t1—t2阶段。t1时，开关管 VT1、VT4死区时间结束，由于此时续流二极管VD1、VD4仍处于导通状态，因此VT1、VT4实现了零电压零电流导通且式（4）适用于该阶段。

d.t2—t′2阶段。t2时，电感电流变为 0，续流二极管 VD1、VD4关断，但由于 VT1、VT4已经导通，因此，uh1保持U1不变，电感电流反向，续流二极管VD6、VD7关断，电流流过V′T2、V′T3。该过程中，由于电感两端电压未发生变化，式（4）仍然适用于该阶段。

e.t′2—t3阶段。t′2时，V′T2、V′T3关断，由于缓冲电容C2、C3电压不能突变，V′T2、V′T3关断过程为零电压关断。与t0—t′0阶段相似，此过程中电感电流为正弦变化，缓冲电容电压与高频链电压uh2均为余弦变化。

f.t3—t′3阶段。与t′0—t1阶段相似，t3时，电容C5、C8上的电荷分别全部转移到电容 C6、C7上，uC5、uC8变为0，uC6、uC7变为U2。由于电感足够大，电感电流并没有反向，因此，续流二极管 VD5、VD8导通，uh2变为nU2。

g.t′3— t4阶段。t′3时，开关管 V′T1、V′T4死区时间结束，由于此时续流二极管VD5、VD8仍处于导通状态，因此 V′T1、V′T4为零电压零电流导通，电路运行状态同 t3— t′3阶段。

由于运行过程的对称性，t4—t8阶段与t1—t4阶段的分析相似，本文不再赘述。

2.2 非缓冲式DAB开关特性与高频环节波形分析

由图1（b）对非缓冲式DAB进行分析，可得如下结论。

a.t0—t′0阶段。与电容缓冲式 DAB 相似，t0前，H1桥开关管 VT2、VT3导通，H2桥开关管 V′T2、V′T3的续流二极管 VD6、VD7导通。t0时，V′T2、V′T3关断，由于没有死区时间，因此VT1、VT4同时导通。由于此时电流通过续流二极管 VD1、VD4，因此，VT1、VT4的导通为零电压导通，但由于没有缓冲电容，VT2、VT3的关断行为将为硬关断，该过程中，高频链电压uh1垂直上升，产生很大的du/dt，此后电路状态同电容缓冲式DAB t′0— t1阶段。

b.t′0—t1阶段。t′0时，电感电流发生反向，该过程与电容缓冲式DAB的t2—t′2阶段相似。

c.t1—t2阶段。与 t0—t′0阶段相似，只是电感两端电压不同、电流变化速度不同。

由于运行过程的对称性，t2—t5阶段与t0—t2阶段的分析相似，本文不再赘述。

3 缓冲电容对软开关行为、du/dt、传输功率以及回流功率的影响

3.1 电容缓冲式DAB与非缓冲式DAB高频环节波形特征与软开关特性比较

由上面的分析可知，非缓冲式DAB由于没有缓冲电容，其正常运行时所有开关管只有在导通时才具有软开关行为，而关断时则为硬关断行为，这种半软开关行为对变换器的损耗是不利的。同时，由于缺乏二阶暂态过程，其高频环节电压均为方波，存在很大的du/dt；高频环节电感电流为分段线性，含有较大的谐波。而电容缓冲式DAB由于缓冲电容的存在，在二阶暂态阶段，高频环节电压均为余弦规律变化，可以显著减小电压du/dt以及电流中的谐波分量。此外，当死区时间满足一定条件时，能够保证所有开关的全软开关运行，明显提高变换器的运行效率，对其死区时间需满足的条件（匹配工作状态下）分析如下：

a.二阶谐振时，4个电容能量第一次交换完毕时间必须小于死区时间；

b.死区时间内，电感电流不变向，即开关管的并联二极管应先于开关管导通。

由此，得到满足全软开关的死区时间条件为：

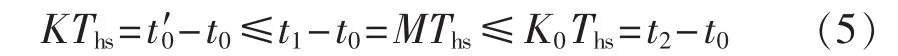
其中，M=Td/Ths，Td为死区时间，Ths为半个开关周期；K=TC/Ths为电容缓冲系数，TC为电容能量交换时间；K0为电流过零点系数。

此外，由匹配运行情况下的对称性可知：

考虑临界条件，即K=K0=M，可得D与K的临界值为：

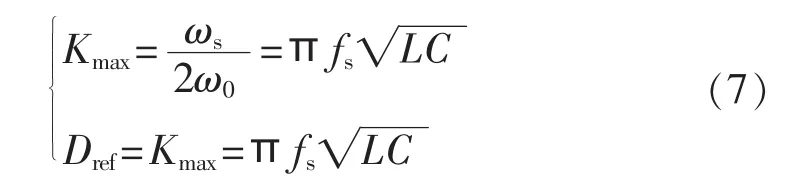
通常情况下，只要移相角大于其临界值便可以根据式（5）选取合适的死区时间，以满足全软开关运行条件。而对于给定的缓冲电容C，可以计算出高频电感电流初始值I0及缓冲系数K的大小。

电容能量交换时间指变换器二阶谐振时电容能量交换一次所需要的时间。由式（2）可知匹配情况下的缓冲电容电压为：

而TCThs为uC1从U1降到0的时间，即TC满足：

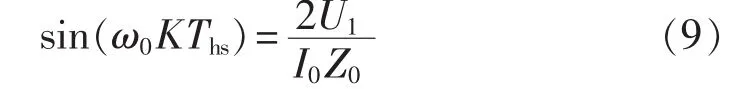
由于变换器运行时所具有的对称性，可得：

求解式（10），可得：

联立式（9）、（11），可得：

综上，可得：

将式（6）、（7）、（13）代入式（5），可得当缓冲电容C一定时，电容缓冲式DAB实现全软开关的死区时间条件为：

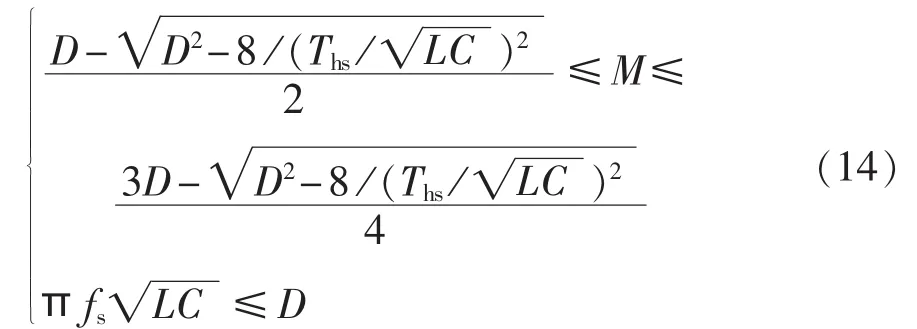
3.2 电容缓冲式DAB与非缓冲式DAB高频环节电压du/dt的比较分析

由2.2节可知，由于缓冲电容的存在，电容缓冲式DAB变压器两端高频链电压的上升沿与下降沿均为余弦规律变化。相比于非缓冲式DAB高频电压的方波，该过程对高频链电压du/dt具有抑制作用，减小了对高频变压器的损害，拓宽了变换器在中高压直流配电网中的应用范围，由式（2）可得电容缓冲式DAB的du/dt大小为：

由式（15）可知，在变换器的运行过程中，高频链电压du/dt的最大值与缓冲电容C的关系为：

图2给出了当工作电压、变压器漏感、工作开关频率为某一定值时，du/dt最大值与移相比D和缓冲电容C的关系。从图中可知，移相比D越大（传输功率越多），du/dt最大值越大；电容 C 越大，du/dt最大值越小，对du/dt的抑制作用越明显。

图2 CBDAB高频环节du/dt最大值与移相比D关系Fig.2 Relationship between the maximum value of du/dt and phase-shift ration D

3.3 电容缓冲式DAB与非缓冲式DAB传输功率以及功率回流的比较分析

为了分析缓冲电容对变换器传输功率和功率因数的影响，分别对电容缓冲式DAB与非缓冲式DAB分析。

由图1（c）可得电容缓冲式DAB的传输功率为：

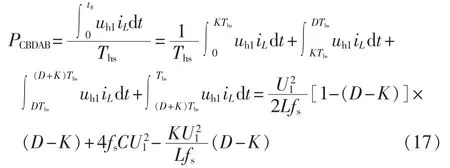
根据文献［10］，可得传统DAB变换器的传输功率为：

比较式（17）与（18）可知，非缓冲式DAB变换器可以视为电容缓冲式DAB在电容缓冲系数K=0（C=0）时的特例。在移相控制中，非缓冲式DAB所能传输的最大功率为：

以该最大值为基准值，可得电容缓冲式DAB与非缓冲式DAB的传输功率标幺值分别为：

由式（20）可知，电容缓冲式DAB与非缓冲式DAB的传输功率表达式可统一表示为：

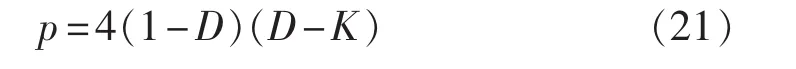
K=0时，p即为非缓冲式DAB的传输功率。

在变换器功率传输的过程中，存在功率返送回电源的阶段，即回流功率阶段，如图1（c）中的 t′0—t2阶段。由文献［10］可知，非缓冲式DAB变换器在匹配时的功率回流表达式为：

同样以非缓冲式DAB的最大传输功率为基准值，可得回流功率的标幺值为：

此外，根据回流功率的定义可以求得电容缓冲式DAB回流功率的标幺值为：

若定义变换器的功率因数F为：

则由式（15）、（18）—（20）可知，电容缓冲式 DAB与非缓冲式DAB的功率因数分别为：

由式（26）可知，电容缓冲式DAB与非缓冲式DAB的功率因数表达式可统一表示为：

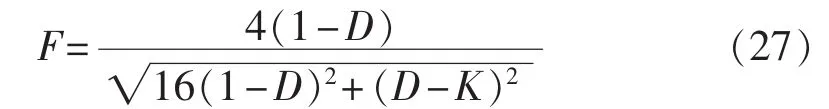
K=0时，F即为非缓冲式DAB的功率因数。

图3为电容缓冲式DAB和非缓冲式DAB的功率因数与移相比的关系曲线。由图可知，当移相比D一定时，由于缓冲电容的影响，电容缓冲式DAB功率因数相比于非缓冲式DAB有所增大，即其回流功率更小，具有更高的传输功率利用率。同时，随着电容缓冲系数K（电容C）增大，电容缓冲式DAB的功率因数随之增大，传输功率利用率也将进一步提高。

图3 CBDAB与非缓冲式DAB功率因数曲线Fig.3 Power factor curves of CBDAB and DAB without buffer

3.4 缓冲电容的取值分析

图4给出了当工作电压、变压器漏感、工作开关频率为某一定值时，du/dt最大值（标幺值，以实际应用中非缓冲DAB的du/dt为基准值）、传输功率（标幺值）与移相比D、缓冲电容C的关系图。从图中可以看出，若缓冲电容的取值过大，则变换器的软开关区域（图中阴影部分）与传输功率最大值将会急剧减小；若缓冲电容的取值过小，则缓冲电容将不能满足对du/dt的抑制作用。因此，缓冲电容的取值应首先在根据变换器运行时的长时间工作状态选择合理的软开关范围之后，考虑传输功率与du/dt的要求，再根据式（14）、（16）、（21）进行合理的选取。

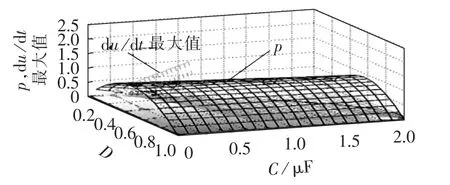
图4 CBDAB传输功率及du/dt最大值与D、C关系图Fig.4 Curve of transmission power of CBDAB and maximum value of du/dt vs.D and C

实际应用中，由于开关管寄生电容值非常小，因此，电容计算值可以直接认为是并联电容的电容值，且对于高频链特征而言，也可以忽略开关管的寄生电容直接考虑并联电容的影响。

4 仿真及样机实验

为了对上述分析的理论进行验证，用仿真软件PSCAD分别搭建了非缓冲式DAB和电容缓冲式DAB的仿真模型，此外还分别搭建了二者的2 kW实验样机。具体参数为：变压器变比n=1，直流电容Cd=2200 μF，缓冲电容 C=110 nF，高频链漏感 L=0.02 mH，变换器开关频率fs=20 kHz。

4.1 仿真实验

图5 CBDAB与非缓冲式DAB软开关对比Fig.5 Soft switching comparison between CBDAB and DAB without buffer

仿真实验中，两端直流电压分别为U1=40 V，U2=40 V，死区系数M=0.2，移相系数D=0.5，以开关管VT1为例，电容缓冲式DAB与缓冲式DAB开关过程的仿真波形如图5所示。图中，UVT1_D与UVT1_C分别为非缓冲式DAB与电容缓冲式DAB开关管两端电压；IVT1_D与IVT1_C分别为DAB与电容缓冲式DAB中流过开关管的电流；IVT1为电容缓冲式DAB中流过开关管反并联二极管的电流。由图可知，当开关管导通时，电容缓冲式DAB与非缓冲式DAB均为零电压零电流导通；当开关管关断时，非缓冲式DAB为硬关断，而电容缓冲式DAB由于缓冲电容的存在，开关管两端电压基本保持为0，实现零电压关断，降低了损耗。

4.2 样机实验

图6与图7分别为非缓冲式DAB与电容缓冲式DAB高频链电压、电流波形。由图6可知，非缓冲式DAB高频链电压上升与下降沿均接近于垂直变化，其du/dt很大，且存在超调及振荡，影响高频变压器磁通，增加变压器噪声，降低变压器寿命。而由图7可见，电容缓冲式DAB高频链电压上升与下降沿均呈余弦规律缓慢变化，其du/dt明显减小，且超调很小，电压变化后并不存在振荡现象。由此，电容缓冲式DAB可有效减小方波调制中的du/dt，从而减小对高频变压器的损害。

图8给出了非缓冲式DAB与电容缓冲式DAB的效率对比结果。右侧输出电源带阻值为12 Ω的电阻负载，通过改变左侧电源输入电压以及右侧电源受控输出电压值，使变流器进行不同的功率传输。从图8中可知，对于不同的传输功率，电容缓冲式DAB的整体传输效率都高于非缓冲式DAB。

图6 非缓冲式DAB高频链电压、电流波形Fig.6 HFL voltage and current waveforms of DAB without buffer

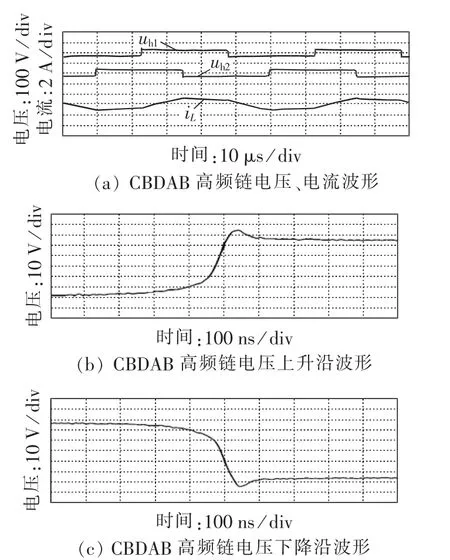
图7 CBDAB的高频链电压、电流波形Fig.7 HFL voltage and current waveforms of CBDAB

图8 CBDAB与非缓冲式DAB效率对比Fig.8 Efficiency comparison between CBDAB and DAB without buffer

通过改变变压器输入电压以及受控输出电压值，使变流器两端的电压形成不同的电压比n，图9给出了变压器不同两端电压比下非缓冲式DAB与电容缓冲式DAB的效率对比结果。从图9中可知，当变压器两端电压匹配时，电容缓冲式DAB和非缓冲式DAB都能获得其最大效率，且它们的效率随着电压比偏离匹配状态而降低；不论变流器两端的电压比如何变化，电容缓冲式DAB的整体传输效率都高于非缓冲式DAB。

图9 不同电压比下CBDAB与非缓冲式DAB效率对比Fig.9 Efficiency comparison between CBDAB and DAB without buffer under different voltage ratios

5 结论

本文对应用于直流配电网的缓冲式DAB与非缓冲式DAB进行了详细的比较分析。首先，从开关特征的角度出发，分析了考虑缓冲电容的高频链电压、电流波形，从而得到缓冲电容对变换器软开关性能、高频环节电压du/dt、传输功率以及功率回流的影响。同时推导了适用于二者的统一传输功率表达式以及回流功率表达式，并指出非缓冲式DAB是缓冲式DAB的特例。然后，分析了缓冲电容的选取方法，得出过大的缓冲电容会降低传输功率最大值以及减小软开关区域，而过小的缓冲电容则不能够满足抑制du/dt的要求等结论。最后，通过实验证明了理论分析的正确性，实验结果同时表明缓冲式DAB比非缓冲式DAB具有更高的传输效率，在直流配电网中将具有更高的应用价值。

参考文献：

［1］施婕，郑漳华，艾芊.直流微电网建模与稳定性分析［J］.电力自动化设备，2010，30（2）：86-90.SHI Jie，ZHENG Zhanghua，AI Qian.Modeling of DC micro and stability analysis［J］.Electric Power Automation Equipment，2010，30（2）：86-90.

［2］王毅，于明，张丽荣.环形直流微网短路故障分析及保护方法［J］.电力自动化设备，2017，37（2）：7-14.WANG Yi，YU Ming，ZHANG Lirong.Short circuit fault analysis and protection scheme for looped DC microgrid［J］.Electric Power Automation Equipment，2017，37（2）：7-14.

［3］宋强，赵彪，刘文华，等.智能直流配电网研究综述［J］.中国电机工程学报，2013，33（25）：9-20.SONG Qiang，ZHAO Biao，LIU Wenhua，et al.An overview of research on smart DC distribution power network［J］.Proceedings of the CSEE，2013，33（25）：9-20.

［4］周稳，戴瑜兴，毕大强，等.交直流混合微电网协同控制策略［J］.电力自动化设备，2015，35（10）：51-57.ZHOU Wen，DAI Yuxing，BI Daqiang，at el.Coordinative control strategy for hybrid AC-DC microgrid［J］.Electric Power Automation Equipment，2015，35（10）：51-57.

［5］杜翼，江道灼，尹瑞，等.直流配电网拓扑结构及控制策略［J］.电力自动化设备，2015，35（1）：139-145.DU Yi， JIANG Daozhuo，YIN Rui，et al.Topological structure and control strategy of DC distribution［J］.Electric Power Automation Equipment，2015，35（1）：139-145.

［6］李勋，龚庆武，胡元潮，等.智能配电网体系探讨［J］.电力自动化设备，2011，31（8）：108-111.LI Xun，GONG Qingwu，HU Yuanchao，et al.Discussion of smart distribution grid system［J］.Electric Power Automation Equipment，2011，31（8）：108-111.

［7］孙栩，王华伟，雷霄，等.架空线柔性直流电网的直流短路电流限制研究［J］.电力自动化设备，2017，37（2）：219-223.SUN Xu，WANG Weihua，LEIXiao，etal.RestrictionofDC short circuit current for overhead lines of flexible DC grid ［J］.Electric Power Automation Equipment，2017，37（2）：219-223.

［8］彭克，张新慧，陈羽.适用于多端柔性互联的交直流配电网潮流计算方法［J］.电力自动化设备，2017，37（1）：22-27.PENG Ke，ZHANG Xinhui，CHEN Yu.Power flow calculation algorithm for AC-DC hybrid distribution network with multi-terminal flexible interconnection［J］.Electric Power Automation Equipment，2017，37（1）：22-27.

［9］江道灼，郑欢.直流配电网研究现状与展望［J］.电力系统自动化，2012，36（8）：98-104.JIANG Daozhuo，ZHENG Huan.Research status and developing prospect of DC distribution network［J］.Automation of Electric Power Systems，2012，36（8）：98-104.

［10］ENGEL S P，SOLTAU N，STAGGE H，et al.Dynamic and balanced control of three-phase high-power dual-active bridge DC-DC converter in DC-grid applications［J］.IEEE Transactions on Power Electronics，2013，28（4）：1880-1889.

［11］赵成勇，李路遥，翟晓萌，等.新型模块化高压大功率DC/DC变换器［J］.电力系统自动化，2014，38（4）：72-78.ZHAO Chengyong，LI Luyao，ZHAI Xiaomeng，et al.A new type of modular high-voltage high-power DC-DC converter［J］.Automation of Electric Power Systems，2014，38（4）：72-78.

［12］ZHAO B，SONG Q，LIU W，et al.Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power conversion system［J］.IEEE Transactions on Power Electronics，2014，29（8）：4091-4106.

［13］赵彪，宋强，刘文华，等.用于柔性直流配电的高频链直流固态变压器［J］.中国电机工程学报，2014，34（25）：4295-4303.ZHAO Biao，SONG Qiang，LIU Wenhua，et al.High-frequencylink DC solid state transformers for flexible DC distribution［J］.Proceedings of the CSEE，2014，34（25）：4295-4303.

［14］BIELA J，SCHWEIZER M，WAFFLER S，et al.SiC versus sievaluation of potentials for performance improvement of inverter and DC-DC converter systems by SiC power semiconductors［J］.IEEE Transactions on Industrial Electronics，2011，58（7）：2872-2882.

［15］XIE Y，SUN J，FREUDENBERG J S.Power flow characterization of a bidirectional galvanically isolated high-power DC-DC converter over a wide operating range［J］.IEEE Transactions on Power Electronics，2010，25（1）：54-66.

［16］ZHAO B，SONG Q，LIU W，et al.Current-stress-optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control［J］.IEEE Transactions on Power Electronics，2013，60（10）：4458-4467.

［17］ZHAO B，SONG Q，LIU W，et al.Dead-time effect of the high frequency isolated bidirectional full-bridge DC-DC converter：comprehensive theoretical analysis and experimental verification［J］.IEEE Transactions on Power Electronics，2014，29（4）：1667-1680.

［18］GERMÁN，GARCÌA，OLIVA A R.Modulation strategy to operate the dual active bridge DC-DC converter under soft switching in the whole operating range［J］.IEEE Transactions on Power Electronics，2011，26（4）：1228-1236.

［19］SHIGENORI I，HIROFUMI A.A bidirectional DC-DC converter for an energy storage system with galvanic isolation［J］.IEEE Transactions on Power Electronics，2007，22（6）：2299-2306.

［20］SIDDHARTH K，RAJAPANDIAN A.Analysis，design，and experimental results of the semidual-active-bridge converter［J］.IEEE Transactions on Power Electronics，2014，29（10）：5136-5147.

［21］NAAYAGI R T，FORSYTH A J，SHUTTLEWORTH R.High-power bidirectional DC-DC converter for aerospace applications［J］.IEEE Transactions on Power Electronics，2012，27（11）：4366-4379.