PI控制器参数对并网永磁直驱型风力发电系统机网相互作用的影响

吴汪平 ，楚皓翔 ，解 大 ，张延迟 ，王西田 ，李国杰

（1.上海交通大学 电气工程系 电子信息与电气工程学院，上海 200240；2.上海电机学院 电气学院，上海 200240）

0 引言

随着环境、能源问题的日益严峻，可再生资源的开发利用已然成为国际热点，其中风力发电技术发展迅猛［1-2］。在不同的风力发电系统中，变速风力发电机具有能量生产效率高和扭矩峰值低的特点，获得了广泛好评［3］。变速风力发电机可以通过调节转轴的速度，使风电系统运行于最大功率点，从而获取最大的风能［4］。直驱型风力发电机在功率密度、效率和可靠性等方面具有优势，完美契合了变速风电系统的运行模式。同时，永磁直驱型风力发电（PMSG）系统能够省略齿轮箱，节约了建造、运行和维护费用［5］，吸引了风力发电机制造商的注意［6］。

目前并网型风电场的规模不断扩大，风电场异常运行的事件越来越多［7-8］。研究发现，风电场与电网之间的相互作用多表现为有功功率的振荡，且对应的振荡频率低于系统工频，与此同时，大规模风电机组出现脱网事故［9］。对此，已有众多学者对PMSG系统的振荡问题进行了研究。文献［10］研究了风电场的非线性模型，并建立了可用于电力系统暂态分析的小信号模型。文献［11］建立了适用于系统小扰动稳定分析的PMSG系统模型，研究了并网风力发电机无穷大系统的模式特性；采用特征值法分析了轴系模型、轴系刚性参数、运行点、并网距离对并网风电系统模式的影响；并在PSCAD/EMTDC上建立了相应的非线性模型，利用Prony方法对输出功率曲线进行模式识别，验证了模态分析结论。文献［12］提出了阻尼控制和峰值功率追踪方案以抑制永磁风电系统的振荡。文献［13］阐述了次同步控制相互作用（SSCI）问题的由来，总结了不同类型风力发电机组的SSCI特性，分析了SSCI的发生机理、参数特性，探讨了SSCI的分析方法及抑制措施。文献［14］利用频率扫描法和特征值分析法对影响SSCI的状态变量进行研究。次同步振荡（SSO）频率与轴系的自然频率接近时，会引发轴系的扭振，长期存在的SSO对系统也是有害的［15］。文献［16］建立了典型PMSG系统接入交流电网的等值系统模型，通过电磁暂态仿真、阻抗模型和小信号分析研究SSO产生的机理；分析接入交流电网强弱、风力发电机出力、并网风力发电机台数、风力发电机控制参数及动态无功补偿设备对振荡特性的影响。低频振荡表现为功率的振荡，该振荡频率较低，一般为0.1~2 Hz，主要由电机的转子出现与其他机组的相对摇摆导致，该振荡模态与励磁系统的弱阻尼相关［17］。文献［18］提出一种综合系统惯性和阻尼控制的PMSG系统稳定器（PSS）控制方案，通过在高风电渗透率电网仿真模型中搭建该控制模块，模拟分析该方案的有效性。在2区域4机系统中进行了时域仿真，结果显示该PSS能有效抑制电网低频振荡。文献［19］提出了粒子群优化算法用于研究PMSG系统的PI控制器参数，以提高系统稳定性。目前缺少以研究系统小扰动稳定性为前提的PMSG系统建模研究，且并网PMSG系统的PI控制器参数对系统振荡问题的影响还缺少系统研究。

本文首先建立了基于 AC/DC/AC变流器PQ解耦控制的PMSG系统的小信号模型。然后，通过特征值分析法找出PMSG系统的振荡模态。根据相关因子表，研究机网相互作用的振荡模态情况，并通过时域仿真验证相应模态的存在。然后，研究变流器的PI控制器参数对各种振荡模态的影响情况。最后，采用基于Copula理论的分布估计算法寻找最优的PI控制器参数组合，并将其代入建立的并网型PMSG系统模型中，观察振荡模态的变化情况。

1 PMSG系统模型

图1为并网PMSG系统拓扑结构。风力发电机直接与永磁同步电机相连，电机输出功率经变流器、输电线路连接至无穷大电力系统，其中变流器是由PWM整流器、逆变器组成的AC/DC/AC变流器。

图1 并网PMSG系统拓扑结构Fig.1 Topology structure of grid-connected PMSG system

PMSG的机侧变流器采用PQ解耦控制策略时，变流器控制如图2 所示。图中，为选定的状态变量；Kp1、Ki1为机侧电流q轴分量PI控制器参数；Kp2、Ki2为机侧电流 d轴分量 PI控制器参数；Kp3、Ki3为网侧直流电压PI控制器参数；Kp4、Ki4为网侧电流d轴分量PI控制器参数；Kp5、Ki5为网侧无功PI控制器参数；Kp6、Ki6为网侧电流 q轴分量PI控制器参数；iqs、iqs_ref分别为机侧变流器电流q轴分量及其参考值；uqs为机侧变流器电压q轴分量；ids、ids_ref分别为机侧变流器电流d轴分量及其参考值；uds为机侧变流器电压 d 轴分量；udc_ref、Qg_ref、idg_ref、iqg_ref分别为网侧直流电压、无功、电流d轴分量、电流q轴分量参考值；udg、uqg分别为网侧电压的 d、q轴分量。网侧变流器主要维持直流侧电容两端电压的恒定，并实现发电机输出有功和无功的最优控制。机侧整流器采用三相桥式6脉冲全波整流电路，以同步发电机组仅输出有功功率而不输出无功功率为控制目标。因此机侧整流器的输入为d轴参考电流Δids_ref和发电机输出的电磁转矩ΔTe，Δids_ref和由ΔTe得到的Δiqs_ref与实际d、q轴的电流偏差，经机侧整流器中的PI控制器调节后可得到目标电压ΔUds、ΔUqs，即输出电压 ΔUs的 d 轴分量、q 轴分量。

图2 机侧PQ解耦的PMSG机组变流器控制Fig.2 Converter control of PMSG unit with PQ decoupling control in generator-side

基于AC/DC/AC变流器PQ解耦控制的PMSG系统的小信号模型如图3所示。图中，ΔTw为风力发电机叶轮部分受风产生的机械扭矩微增量；Δωr为ΔTw和ΔTe共同作用在轴系部分得到的角速度微增量；ΔUs为机侧整流器输出的参考电压微增量；ΔIs为永磁发电机模型的输出电流微增量；ΔUg和ΔIL分别为风电机组的母线电压和输出电流微增量；ΔUb为无穷大电网电压微增量；ΔUDC、ΔUDC_ref分别为网侧直流输入电压及参考值的微增量；ΔQg_ref为网侧无功注入值的微增量。

图3 机侧PQ解耦的PMSG机组小信号模型Fig.3 Small-signal model of PMSG unit with PQ decoupling control in generator-side

由图3可得，机侧整流器采用PQ解耦控制策略的PMSG小信号模型的状态空间表达式为：

其中，ΔXPMSG、APMSG、BPMSG和 ΔuPMSG分别为小信号模型的状态向量（17×1 阶）、系统矩阵（17×17 阶）、输入矩阵（17×5 阶）和输入向量（5×1 阶）；下标 0 表示运行稳态点的值；ωb为系统基准频率；H1、H2分别为质量块1、2的惯性常数；D1、D2分别为质量块 1、2的自阻尼系数；k12和D12分别为质量块1与2之间的刚度系数和互阻尼系数；Lds为定子d轴电感；Lqs为定子q轴电感；ψPM为转子永磁体磁链的幅值；npp为发电机极对数；x为线路的电感；ψds0为稳态时定子d轴磁链；ψqs0为稳态时定子q轴磁链。

2 PMSG系统机网相互作用分析

2.1 特征值分析

由于在采用“背靠背”型全功率变流器后，机侧整流器的控制环节中包含2个PI控制器，因此该小信号系统依然有17个状态变量，即：

其中，Δθi和 Δωi（i=1，2）分别为质量块 i的机械旋转角微增量和角速度微增量；Δψds和Δψqs分别为发电机d轴和q轴磁链微增量；Δx1和Δx2为机侧变流器控制系统变量微增量；Δx3、Δx4、Δx5、Δx6为网侧变流器控制系统变量微增量；ΔiLx、ΔiLy分别为电感电流的 x轴分量、y轴分量微增量；Δucx、Δucy分别为串补电容电压x轴分量、y轴分量的微增量。利用MATLAB搭建PMSG系统小信号模型进行仿真分析，变流器控制参数如下：Kp1=5，Kp2=2，Kp3=0.05，Kp4=6.5，Kp5=0.04，Kp6=20，Ki1=10，Ki2=0.03，Ki3=20，Ki4=50，Ki5=1，Ki6=1。系统全部特征值见表1。

表1 PMSG机组的特征值Table 1 Eigenvalues of PMSG unit

由表1可以看出，系统17个特征值的实部全部小于0，因此机侧整流器采用PQ解耦控制策略后，系统仍然是小干扰稳定的。系统共有5对共轭复根，对应5种振荡模态，剩余的7个虚部为0的负实根对应7种非振荡模态。本文不讨论7种非振荡模态，仅分析5种振荡模态。为确定与各振荡模态相关度较高的状态变量，计算5种振荡模态关于各状态变量的相关因子，见表2。对各种振荡模态影响较大的相关因子在表2中加粗标出。

表2 PMSG机组的相关因子Table 2 Correlation factors of PMSG unit

2.2 机网相互作用模态分析

a.SSCI。

λ1，2对应的振荡频率为 71.454 0 Hz，由输电线路电感电流的x轴分量和y轴分量主导，此外，串补电容电压的x轴分量和y轴分量对其也有一定的影响（相关因子分别为0.033 6和0.064 0），变流器直流侧电容的电压和网侧逆变器的直流电压控制环节与该模态也有一定的关系；λ3，4对应的振荡频率为38.2284 Hz，由输电线路串补电容电压的x轴分量和y轴分量主导，同时，输电线路电感电流的x轴分量和y轴分量对其也有一定的影响（相关因子分别为0.0256和0.0786），变流器直流侧电容电压和网侧逆变器的直流电压控制环节与该模态也有一定关系。这表明 λ1，2和 λ3，4对应的振荡模态是由含串补电容的输电线路、变流器直流电容及网侧逆变器的控制系统共同作用所产生的谐振，属于SSCI。

λ5，6对应的振荡频率为 7.5657 Hz，由变流器直流侧电容的电压和网侧逆变器直流电压控制外环主导，同时与含串补电容的输电线路和网侧逆变器直流电容控制环节的电流控制内环也有一定关系（相关因子依次为 0.052 7、0.040 2、0.022 4、0.025 7和0.001 2）。因此，该振荡模态也是输电线路、变流器直流侧电容和逆变器的控制系统之间相互作用产生的谐振，也属于SSCI。

b.SSO。

λ7，8对应的振荡频率为 1.8703 Hz，由表2 可见，发电机转子的机械扭转角和角速度对其影响较大，且风力发电机的机械扭转角和角速度对其也有一定的影响（相关因子均为 0.053 5），这表明 λ7，8是PMSG机械轴系的固有扭振频率，是机械振荡模态。此外，该振荡模态还与发电机的q轴磁链有一定的关系（相关因子为0.0323），而系统中的其他部分对该模态没有影响，表明“背靠背”型全功率变流器将发电机组与电网有效隔离开，使两者之间具有一定的独立性。

c.低频振荡。

λ14，15对应的振荡频率为 0.134 9 Hz，由发电机的d轴磁链和机侧整流器的控制系统主导（相关因子均为0.512 2），而与系统的其他部分之间没有关系，因此该振荡模态是单机系统的发电机与机侧整流器控制系统相互作用产生的低频振荡模态。

2.3 基于Copula理论的分布估计算法

本文所建PMSG的小信号模型涉及多组PI控制器参数，不同组的PI控制器参数间也存在相互耦合的问题。为了解决多变量相关的寻优问题，本文采用基于Copula理论的分布估计算法，主要包括优势群体选择、概率分布模型估计和根据估计的模型采样3个步骤。

分布模型为了优化变量的联合分布，可以利用Sklar定理对群体的分布模型进行估计。为了产生服 从联合分布 H（x1，x2，…，xn） =C（F1（x1），F2（x2），…，Fn（xn））的个体，首先生成服从联合分布 C 的［0，1］n空间中的点（u1，u2，…，un），然后依据边缘分布函数Fi（i=1，2，…，n）的反函数 F-1i计算获得 xi的值，此时（x1，x2，…，xn）就为根据估计的概率模型 H 采样而获得的新个体。

基于Copula理论的分布估计算法的基本流程如图4所示。在搜索空间中，采取均匀分布的方式产生规模为PS的初始群体，随后分别执行以下步骤直至达到终止条件。

a.选择优势群体。基于设定的、符合适应值的选择策略，选择s个个体来组成新的优势群体，记为：

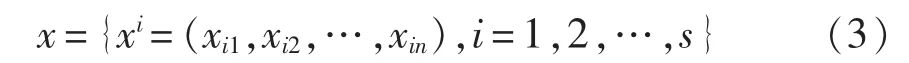
b.估计边缘分布函数。优势群体中的s个个体是 n 维随机向量（X1，X2，…，Xn）的 s 个样本，那么｛xij，i=1，2，…，s｝就是随机变量 Xj的样本，据此可估计边缘分布函数为 Fj（j=1，2，…，n）。

c.从Copula函数C中采样。产生l个服从联合分布函数C的向量。

图4 基于Copula理论的分布估计算法原理图Fig.4 Schematic diagram of estimation of distribution algorithm based on Copula theory

d.更新群体。新的群体分为以下三部分：当前代群体中的适应值最好的m个个体；通过计算得到l个新的个体；在搜索空间中按均匀分布随机产生其余的PS－m-l个个体。

3 时域模型验证

为了进一步验证上述小信号模型中各个振荡模态的振荡频率，在MATLAB/Simulink中搭建2MW基于AC/DC/AC变流器PQ解耦控制的PMSG的时域模型，通过输电线路连接至无穷大电网。采用电压波动、功率波动等小扰动方式激发振荡，利用Simulink的快速傅里叶变换（FFT）分析工具，结合表2给出的相关因子，在相应的相关变量上进行观测，可以发现与上述分析对应的全部机网相互作用模态，如图5所示，图中Mag为谐波分量幅度。

a.SSCI。

上述小信号模型分析表明，λ1，2和 λ3，4对应的振荡模态与输电线路电流和串补电容的端电压有很强的相关性，同时变流器直流侧电容的电压对其影响也较大，对输电线路流过的电流进行频谱分析，得到其对应频谱特性如图5（a）所示。输电线路流过的电流中，主要含有70 Hz和38 Hz左右的谐波成分，这与 λ1，2对应的振荡频率 71.4540Hz、λ3，4对应的振荡频率38.2284Hz相吻合。

表2中的相关因子表明，λ5，6对应的振荡模态由直流电容两端的电压和网侧逆变器的控制系统主导，对直流电容的电压进行频谱分析，得到其频率特性如图5（b）所示。在直流电容的电压中除去直流分量外，主要还有8Hz左右的谐波成分，这与模态λ5，6的振荡频率7.5657 Hz相吻合。

b.SSO。

通过相关因子分析可以发现，λ7，8所对应的振荡模态由发电机的转子主导，因此，分析发电机的转子转矩，其对应的波形和频谱特性如图5（c）所示。发电机的转子转矩中除去直流分量外，主要还有1.9Hz左右的谐波成分，这与模态λ7，8的振荡频率1.8703Hz相吻合。

图5 时域仿真波形及其频谱分析Fig.5 Waveforms and spectral analysis of time-domain simulation

c.低频振荡。

通过相关因子分析可以发现，λ14，15所对应的振荡模态由d轴磁链和机侧整流器的控制系统主导，而发电机的d轴电流决定了d轴磁链，因此，分析发电机的d轴电流，其对应的波形和频谱特性如图5（d）所示。发电机的d轴电流中除去直流分量外，主要还有0.2Hz左右的谐波成分，这与模态λ14，15的振荡频率0.1349Hz相吻合。

4 变流器PI参数对振荡模态的影响

基于AC/DC/AC变流器PQ解耦控制的PMSG系统共存在SSO、SSCI和低频振荡3种振荡模态，如表3所示。

表3 并网PMSG机组的振荡模态Table 3 Oscillation modes of grid-connected PMSG unit

4.1 单PI控制器参数作用分析

由于表3中3种振荡模态均与变流器控制PI参数紧密相关，为了研究各控制模块的PI参数变化对系统各个振荡模态的影响，依次改变各PI参数，保持其他变量不变，得到系统各种振荡模态对应的阻尼比的变化。实际中，风电场与电网之间的相互作用多表现为有功功率的振荡，故本文以与功率密切相关的PI参数Kp4为例，其他PI参数的研究方法与其类似。

研究PI参数Kp4的变化对系统各个振荡模态的影响，保持其他变量不变，Kp4以1为步长从1变化到100，得到系统各种振荡模态下所对应的特征值的实部和阻尼比的变化关系，如图6所示。其中，Kp4对SSO和低频振荡无影响。

考虑各个振荡模态随Kp4的变化特性，系统最佳Kp4见表4。系统最佳Kp4的范围为40~43，相应的各个振荡模态运行范围如图6中椭圆虚线所示。

4.2 多PI控制器参数作用分析

针对多组PI控制器参数的不确定性问题，本节采用基于Copula理论的分布估计算法，寻找PI控制器参数的最优组合，其最佳PI控制器参数如表5所示。

利用表5给出的PI控制器参数对PMSG振荡模态进行分析，各振荡模态详细信息见表6。

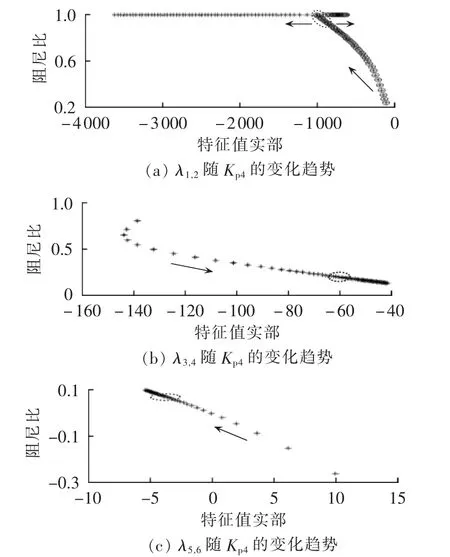
图6 各振荡模态随Kp4的变化趋势Fig.6 Variation trend of oscillation modes vs.Kp4

表4 Kp4对各振荡模态阻尼比的影响Table 4 Effect of Kp4on damping ratio of oscillation modes

表5 PMSG机组变流器最佳PI控制器参数Table 5 Optimal PI controller parameters of PMSG converter

表6 PMSG机组变流器最佳PI控制器参数对应的各种振荡模态Table 6 Oscillation modes of PMSG converter corresponding to optimal PI controller parameters

由表6可知，系统共出现2个振荡模态，与表3相比，λ1，2和 λ5，6对应的 SSCI模态，以及 λ14，15对应的低频振荡模态都消失了。这说明，通过合理的变流器控制PI参数调节可以起到减弱甚至消除SSCI以及低频振荡。另外，SSO模态λ7，8对应的阻尼比由0.003 0增大为0.017 7，这说明通过优化变流器控制PI参数可以增大SSO模态对应的阻尼比，起到减弱轴系振荡的目的。

5 结论

本文以基于AC/DC/AC变流器PQ解耦控制的PMSG系统为例，研究风力发电系统的振荡问题。从系统稳定性出发，尝试将直驱型风电系统的振荡问题与变流器控制联系起来，通过改变变流器控制参数抑制甚至消除系统的振荡。本文主要结论如下。

a.本文对建立的PMSG系统模型进行了详细的分析，确定了系统所有的振荡模态。PMSG系统存在5种振荡模态，其中包含3种SSCI振荡模态、1种SSO模态和1种低频振荡模态。SSCI振荡模态和低频振荡模态均与变流器控制密切相关，SSO模态与机侧变流器相关。

b.通过参数优化，部分SSCI振荡模态消失，所有的低频振荡模态也消失，同时可以增大SSO的阻尼比。本文所提控制器的参数优化方法在实际风电场中获得了广泛的应用，是当前风电机网相互作用的主要解决方案。

c.本文采用基于Copula理论的分布估计算法进行了多控制参数的寻优，优化方法可以扩大PI控制器参数的优化域，相比仿真试探法可以得到更加优化的控制参数的组合方式。实际结果验证了算法的可用性。

参考文献：

［1］康劲松，张烨.多电平变流器在风力发电系统中的应用［J］.中国电机工程学报，2009，29（24）：20-25.KANG Jinsong，ZHANG Ye.Multi-levelconverterapplied to wind power generation system［J］.Proceedings of the CSEE，2009，29（24）：20-25.

［2］王冕，陈国柱.风电背靠背 PWM 变流器直流能量平衡新方法［J］.电力自动化设备，2016，36（7）：28-33.WANG Mian，CHEN Guozhu.DC energy balance scheme for back-to-back PWM converters of wind power system［J］.Electric Power Automation Equipment，2016，36（7）：28-33.

［3］CARLIN P W，LAXSON A S，MULJADI E B.The history and state of the art of variable-speed wind turbine technology［J］.Wind Energy，2003，6（2）：129-159.

［4］ZHANG Z，ZHAO Y，QIAO W，et al.A space-vector-modulated sensorless direct-torque control for direct-drive PMSG wind turbines［J］.IEEE Transactions on Industry Applications，2014，50（4）：2331-2341.

［5］QIAO W，YANG X，GONG X.Wind speed and rotor position sensorless control for direct-drive PMG wind turbines［J］.IEEE Transactions on Industry Applications，2012，48（1）：3-11.

［6］LI S，HASKEW T A，SWATLOSKI R P，et al.Optimal and direct-current vector control of direct-driven PMSG wind turbines［J］.IEEE Transactions on PowerElectronics，2012，27（5）：2325-2337.

［7］KUMAR P.Effect of increasing rated torque of PMSG with variable wind speed on per phase output voltage for off-grid wind energy conversion system［C］∥2015 Second International Conference on Advances in Computing and Communication Engineering（ICACCE）.Dehradun，India：IEEE，2015：49-52.

［8］SAINZ L，MONJO L，PEDRA J，et al.Effect of wind turbine converter control on wind power plant harmonic response and resonances［J］.IET Electric Power Applications，2017，11（2）：157-168.

［9］何世恩，董新洲.大规模风电机组脱网原因分析及对策［J］.电力系统保护与控制，2012，40（1）：131-137.HE Shien，DONG Xinzhou.Cause analysis on large-scale wind turbine tripping and its countermeasures［J］.Power System Protection and Control，2012，40（1）：131-137.

［10］MOHAMMED A M，IRAVANI R.Enhanced generic nonlinear and linearized models of wind power plants［J］.IEEE Transactions on Power Systems，2017，32（5）：3968-3980.

［11］谭谨，王晓茹，陈哲.并网永磁直驱式风电系统的模态分析［J］.电力系统保护与控制，2013，41（17）：49-55.TAN Jin，WANG Xiaoru，CHEN Zhe.Modal analysis of a gridconnected direct-drive permanent magnet synchronous generator wind turbine system［J］.Power System Protection and Control，2013，41（17）：49-55.

［12］HSU P，MULJADI E.Damping control for permanent magnet synchronous generators and its application in a multi-turbine system［C］∥2014 Australasian Universities Power Engineering Conference（AUPEC）.Perth，WA，Australia：IEEE，2014：1-6.

［13］高本锋，刘晋，李忍，等.风电机组的次同步控制相互作用研究综述［J］.电工技术学报，2015，30（16）：154-161.GAO Benfeng，LIU Jin，LIRen，etal.Studiesofsub-synchronouscontrolinteraction in wind turbine generators［J］.Transactions of China Electrotechnical Society，2015，30 （16）：154-161.

［14］SURIYAARACHCHI D H R，ANNAKKAGE U D，KARAWITA C，et al.A procedure to study sub-synchronous interactions in wind integrated power systems［J］.IEEE Transactions on Power Systems，2013，28（1）：377-384.

［15］ANONYMOUS.Terms，definitionsandsymbolsforsubsynchronous oscillations［J］.IEEE Transactions on Power Apparatus&Systems，2007，PAS-104（6）：1326-1334.

［16］谢小荣，刘华坤，贺静波，等.直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析［J］.中国电机工程学报，2016，36（9）：2366-2372.XIE Xiaorong，LIU Huakun，HE Jingbo，et al.Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems［J］.Proceedings of the CSEE，2016，36（9）：2366-2372.

［17］薛禹胜，郝思鹏，刘俊勇，等.关于低频振荡分析方法的评述［J］.电力系统自动化，2009，33（3）：1-8.XUE Yusheng，HAO Sipeng，LIU Junyong，et al.A review of analysis methods for low-frequency oscillations［J］.Automation of Electric Power Systems，2009，33（3）：1-8.

［18］彭章刚，周步祥，冯超.基于PMSG-PSS的高风电渗透率电网低频振荡分析［J］.高压电器，2016（6）：147-152.PENG Zhanggang，ZHOU Buxiang，FENG Chao.Analysis of low frequency oscillation for power system with large wind power integration based on PMSG-PSS［J］.High Voltage Apparatus，2016（6）：147-152.

［19］SUN L，GONG C， HAN F.Design and optimization of control parameters based on direct-drive permanent magnet synchronous generator for wind power system［C］∥2013 8th IEEE Conference on Industrial Electronics and Applications（ICIEA）.Melbourne，VIC，Australia：IEEE，2013：1238-1243.