发现学习理论在高等数学教学中的实践研究

丁玉梅 王 霞

（天津科技大学 天津 300222）

发现学习理论在高等数学教学中的实践研究

丁玉梅 王 霞

（天津科技大学 天津 300222）

基于美国教育学家布鲁纳提出的发现学习理论，针对高等数学课堂教学，阐述了发现学习理论的主要内容和发现学习的思维过程，强调学生在数学学习过程中，要先理解领会知识体系，保持知识结构的完整性、系统性，形成良好的认知结构。最后提出如何在高等数学教学中运用发现学习理论，主要包括在概念教学中的多重体现方法；在公式教学中创设数学学习情境；在问题解决过程中，进行合情推理、展示思维过程等。运用发现教学法，能够调动学生学习的积极性，培养数学思维能力。

发现学习理论；认知结构；数学教育

一、研究的意义

高等数学作为一门基础学科，内容多，课时少，考试压力大。怎样才能高效率地吸收知识，提高思维能力和问题解决能力，是师生面临的困惑。当今时代，随着信息科学的发展，各种教学法的改革也层出不穷。但是从根本上来讲，教师课堂教学，多数只注重知识的传授，很少给学生独立思考的时间和空间。怎样把数学知识和思维方法教给学生仍然是很关键的问题。对普通院校学生来讲，由于受高考应试教育的影响，主动学习能力差，仅限于被动接受知识，学习积极性不高，解决实际问题能力不强。数学教育的主要目的，是使学生掌握一定的数学知识、数学思想和方法，提高学生的数学素质，培养他们的思维能力、创造性和应用能力。

布鲁纳提出的发现学习理论，从认知结构出发对学习过程进行研究，在世界教育史上影响深远。本文从认知心理学的角度出发，结合发现学习理论，遵循学生接受知识的心理过程，对大学高等数学教学法改革进行实践研究与探讨。

二、发现学习理论的主要内容

1.发现学习的定义

发现学习理论是美国著名教育心理学家布鲁纳提出来的，瑞士心理学家皮亚杰和美国心理学家斯金纳也都先后提出过这种思想。按照发现学习理论，学习被认为是通过认知获得意义和表演，从而形成认知结构的过程。发现法学习，即在教师的指导下，由学生用探索、发现、研究的方式来获得新的知识。发现学习被看成是由有意义的接受型学习向发现型学习的发展。学生个人的主动性和在学习过程中的参与程度，对于概念形成、知识的保持和知识的运用方面都起到积极的作用。教师在课堂教学过程中，由原来的讲授型教学，转化为学习型教学，由原来的解释型教学，转化为发展型教学；相应的，学生的学习就会由原来被动接受知识的传递过程，转化为发挥主动精神来获取知识的过程。

2.发现学习理论的主要内容

任何学科都有自己的知识体系和结构，大学数学课程也不例外。以高等数学课程为例，我们学习的主要内容是微积分，其中极限思想贯穿于整个学习的始终。因此，由简单到复杂，我们先学习了极限、重要极限，接着用极限定义了导数和积分；由一元函数求导数，拓展为多元复合函数的偏导数；由积分拓展为重积分和线面积分等等。基于知识结构的系统性，学生要由浅入深，由简单到复杂把握学习内容，建立自己的认知结构。

现代教育理论认为，通过教师讲授的学习属于有意义接受性学习，学生的认知结构处于被动的接受状态，经过教师详细剖析的知识，虽然易于被学生接受，但是由于新知识在学生的认知结构中被动加工的程度低，和原有认知结构中起固定作用的概念联系松散，可辨别度和可分离度都较低，这样的知识不利于记忆也不利于知识的保持。由于学生接受的是经过教师过分加工过的材料，思维训练中紧张程度差，也不利于培养思维能力。

对学生来讲，形成良好的认知结构，需要在教师的指导和引导下，发挥主观能动性，自觉主动的去获取知识，进行有意义的知识建构。同时，还要利用原有的认知结构，进一步积极地思考分析和探究新问题，进行问题解决，并形成新的认知结构。学生主动学习的过程是一个发现掩藏知识的过程，只要能够找到正确的方法和新旧知识联结的关键点，运用学习策略，就可以把隐藏的答案找出来，从而循序渐进地学习大量新知识。

对教师来讲，要了解学生的学习过程，尝试在教学过程中要扮演引导的角色。为此，教师首先要不断进行学习积累，具有广博的知识，能够对学生的学习过程进行预测和控制。在学生进行问题探究的过程中，在学生思维出现矛盾点时，进行指点，引导他们找出新旧知识的关联点；在学生思维出现混乱时，及时进行引导，对错误的信息进行修正。教师要引导学生独立地思考探究，遵循学习规律，探索知识的真谛。

3.发现法学习的思维过程

布鲁纳特别强调发现在学习过程中的作用。他认为，“强调学习过程的发现确实影响着学生，使他们成为一个知识的主动建构主义者。这使学生对遇到的失误加以组织时持有一种积极的态度，它使学生不仅想发现规律性和联系性，而且还想使信息处于能控制的状态，以保持信息发挥其可能发挥的作用”。“发现不限于那种寻求人类尚未知晓的事物的行为，发现还包括用自己的头脑亲自获得知识的一切形式。”

布鲁纳认为，认知结构、表征或者表征系统，是人们发现和认识世界的一种能力。认知结构一经建立，就成为学生进一步学习的重要因素。在理解新知识上起到了铺垫作用，也成为对新的信息进行加工的根本。新知识的学习过程，就是利用知识储备，对新知识进行加工改造，使之与旧知识相关联并形成新的认知结构，从而获得新知识。

发现法学习的思维过程包括：知识准备，提出问题，对问题进行思考分析，提出解决问题的方法，最后总结，通过比较选定最佳答案。学生首先头脑中要有一定的知识储备，特别是相关内容的知识，构成原有认知结构。提出相应的问题，学生通过提取原有认知结构中相关的知识，去思考，进行分析。如果能够利用原有知识进行解决，就利用原有旧知识，同化新知识，把新知识消化吸收，纳入原有的认知结构。如果利用原有知识解决出现困难，就利用旧知识，进行原有认知结构的改组，顺应新知识，进行问题解决，由此进行新的认知结构的重建。最后，通过总结，选定最佳答案。这样，通过发现法学习，不仅解决了提出的问题，还从问题解决的过程中，获得了新知识，构建了新的认知结构。

三、发现学习理论在高等数学教学中的实践研究

在大学数学教学中，对于概念、定理、解题的教学环节，通过渗透发现学习理论，使学生遵循学习规律去学习，使其认知结构、学习能力和学习效率得到提升。事实证明，如果允许学生去思考、假设和用直接的方式去产生和体验教学思想的成长，发现式的学习和教学方法将更有效。

1.概念教学中的多重体现方法

发现法的学习方式被认为对学生建立数学概念来说是有效的。例如，高等数学教学过程中，关于定积分的定义，可以这样进行课堂教学设计，让学生进行自主探究。

知识准备：极限的定义，规则图形（如矩形、梯形）的面积。

提出的问题：求解曲边梯形的面积；求变速直线运动的路程。

最后，引导学生在学习过程中，进行总结：虽然求面积和求路程分别属于几何、物理两种不同的问题，但处理的方法本质是一样的，即都可以归结为求某种乘积和式的极限形式，具有普遍性，从而引出定积分的定义。统一的概念和结构的出现对把不同概念彼此联系起来是十分有效的。

2.创设数学学习情境，进行公式教学

发现法学习把重点放在发现关系和再构造某种数学学习情境。例如，在导数的定义教学中，学生对定义的理解都很含糊，通过创设学习情境，对变量增量的各种形式进行辨析，进行认知结构的构建。

提出问题：设f（x）在x=a处可导，判断下列式子是否正确：

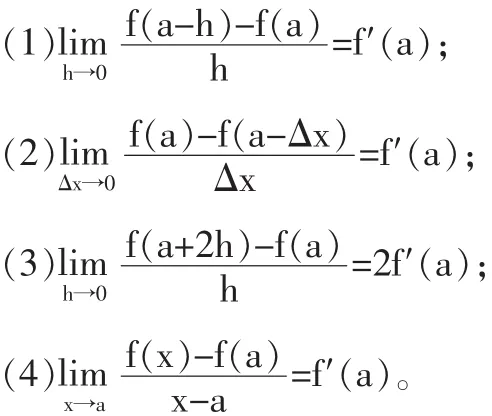
在知识准备阶段，引导学生复习导数的定义，得到下面公式：

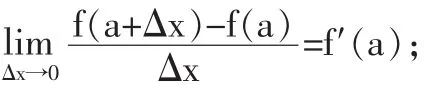
通过对上述公式的分析，明确增量Δx的整体性。得到：

如果令Δx=x-a，则得到：

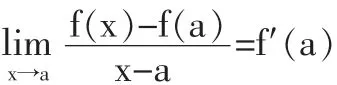
最后总结，式子（1）错误，式子（2）（3）（4）正确。

在同一学习阶段，从许多不同的方面或者途径呈现同一数学公式，以便使学生通过系统的加强和再构造各种结果而形成对公式概念的更一般的理解，得到更精确的思想和确切的概念表述。

3.问题解决教学中，进行合情推理，体验发现过程，提高思维能力

发现学习强调善于引导学生“发现”各种规则、适当的定义或者公理的证明步骤，以此代替那些使用现成的公式、假设、证明的表达的做法。比如，在“牛顿-莱布尼兹”公式的教学中，我们进行合情推理，遵循思维过程，设计了下面的教学案例。

（1）写出不定积分的计算公式：

∫f（x）dx=F（x）+C，其中F（x）是f（x）的一个原函数，C是任意常数。进行猜想，问题的结论一定与原函数F（x）有关。

（2）思考原函数具有什么性质？引出公式，其中F（x）和G（x）都是f（x）的原函数。因此，需要找出一个原函数。进行猜想：

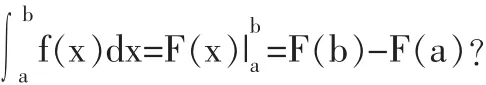
（4）引导学生学习新知识，引入积分上限函数的概念，得到f（x）的另一个原函数，即：

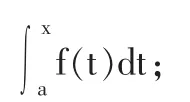
（5）原函数的性质：

（6）进行合情推理，令x=a，x=b得到结论。

在学生还没有认识公式之前，先利用原有认知结构进行猜想，接着引入积分上限函数，通过寻找原函数，引导他们做出自己的发现。再如求解一元线性非齐次方程的常数变异法，伯努利方程的求解过程等等，都是很好的思维训练的题目。在问题解决过程中，教学重点是运用合情推理，展示思维过程，培养问题解决的能力。

另外，在课堂教学的过程中，还要协调师生协作关系，激发学生学习积极性，体验成就感、满足感和成功之后的愉悦感，这样能够强化发现学习的乐趣，培养学生主动学习的习惯。通过近两年的高等数学发现法的实践教学，学生的数学学习成绩明显提高，创新活动中的思维能力比较活跃，这说明学生的数学学习能力提高，解决实际问题的能力和创新能力也进一步增强。总之，在大学高等数学课堂教学过程中，要坚持发现学习和接受学习相结合，加强教师主导，不忽略学生的主体地位，才能实现更高的教育目标。

[1]布鲁纳.教育过程[M].邵瑞珍，译.北京：文化教育出版社，1982.

[2]王光明，佘文娟，宋金锦.基于NVivo10质性分析的高效数学学习心理结构模型[J].心理与行为研究，2014，12（1）：74-79.

[3]郑毓信.“数学与思维”之深思[J].数学教育学报，2015，24（1）：1-5.

[4]王霞，丁玉梅.高等数学课程教学中学生辩证思维能力的培养[J].中国轻工教育，2016（3）：36-39.

[5]张顺燕.数学的思想、方法和应用[M].北京：北京大学出版社，2003.

[6]林崇德.学习心理学丛书[M].武汉：湖北教育出版社，1999.

[7]胡李盈.布鲁纳的认知——发现学习理论对数学学习的启示[J].高等教育，2015（12）：76-77.

（责任编辑：张华凡）

Application of Discovery Learning Theory in the Teaching of Advanced Mathematics

DING Yumei,WANG Xia
（Tianjin University of Science and Technology,Tianjin 300222,China）

The main content and process of the discovery learning theory are introduced based on the discovery learning theory proposed by American educator Bruner.In the process of mathematics learning, students should understand the knowledge as well as its systematic structure,and then form a good cognitive learning pattern.The application of discovery learning theory in the teaching of advanced mathematics should include multiple methods of concept teaching,creation of mathematics learning environment in formula teaching and plausible reasoning in the process of problem-solving.As a result,the discovery teaching has improved the students’interest in mathematics and their maths thinking abilities.

discovery learning theory;cognitive structure;mathematics education

G642.0

丁玉梅（1972—），女，副教授，研究方向：数学教育。

天津市教育科学“十三五”规划重点课题（HE1020）。