一种基于多普勒效应的拟牛顿室内定位算法
2017-05-18张晓燕孙婷婷徐新民
张晓燕, 孙婷婷, 徐新民*
(1. 浙江长征职业技术学院, 浙江 杭州 310023; 2. 浙江大学 信息与电子工程学院, 浙江 杭州 310027)
一种基于多普勒效应的拟牛顿室内定位算法
张晓燕1, 孙婷婷2, 徐新民2*
(1. 浙江长征职业技术学院, 浙江 杭州 310023; 2. 浙江大学 信息与电子工程学院, 浙江 杭州 310027)
针对现有室内定位方法,根据目标节点在运动过程中与参考信标节点间产生的多普勒效应,得到一种距离差测量方法,避免了对目标节点与信标节点间时钟同步的要求.为实现此距离差定位,提出了一种基于拟牛顿法的室内定位算法.随机选取初始猜测值,得到一个测量点的距离差信息,由此迭代得到单个测量点坐标,再将所有测得的相对位置坐标进行整体迭代并调整初始位置,直到得到稳定的初始位置,实现定位.Matlab仿真结果表明,在信噪比SNR=10时,定位误差不超过0.5 m.同时,为提高定位速度和成功率,尝试用粒子群算法求初始猜测值,进一步提高算法的性能.
多普勒效应;拟牛顿迭代;室内定位
Journal of Zhejiang University(Science Edition), 2017,44(3):322-326
0 引 言
随着社会发展和科技进步,基于位置的信息服务备受关注,在物流监控、学生监护、老弱病残的追踪护理等中有大量需求,室内定位技术已成为关注和研究的热点.目前,常用的室内定位技术有结合网络基站信息和GPS信息的A-GPS技术[1]、超声波测距法、蓝牙定位[2]及射频识别技术[3]等.以上室内定位方法分2步实现,首先通过RSSI (received signal strength indicator)、TOA(time of arrival)或TDOA (time difference of arrival)测得目标节点和信标节点之间的距离或距离差,然后通过三边定位、质心定位等方法计算目标节点的具体位置.但这些方法对室内环境及其稳定性或收发目标节点的时钟同步和精度要求较高.
为降低对室内环境和时钟同步的要求,本文引入一种基于多普勒效应的定位系统模型.文献[4]所介绍的基于多普勒效应的定位方法,主要为运动观测站(信标节点)相对于固定辐射源(目标节点)的测量频差的定位法,对硬件要求严格.本模型利用目标节点在运动过程中与固定信标节点间的多普勒效应,测量运动过程中目标节点不同位置到同一节点的距离差并进行定位.该距离差测量值与目标节点在运动过程中的前后节点位置有关,因此无法再利用传统的三边定位等算法.本文将定位问题转化为最小值优化,采用拟牛顿算法(BFGS)求解.随机选取初始值后,基于测量值信息的累积多次迭代调整,得到稳定初始位置以实现较高精度的定位.同时,用粒子群算法进一步提高定位精度.实验和Matlab仿真证明该方法精度较高,是一种可以尝试的定位方法.
1 定位测距模型
1.1 测距原理
多普勒效应是指发射源与观察者间有相对运动时,观察者接收到的波的频率与波源发出的频率不相等的现象.当观察者位置保持不变而发射源在运动时,两者的频率关系为
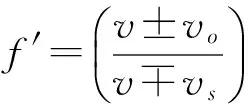
(1)
其中,f′为观察到的频率;f为发射源于该介质的原始发射频率;v为波在该介质中的行进速度;vo为观察者的移动速度,若接近发射源则前方运算符号为‘+’,反之则为‘-’;vs为发射源移动速度,若接近观察者则前方运算符号为‘-’,反之则为‘+’.
本文以目标节点为发射源,在运动过程中发射同频率的正弦波,则信标节点接收到的是频率改变的正弦波.假设目标节点在Pj位置发射了正弦波的第j个过零点(zero-crossing),此时刻为tT1,在Pj+1位置发射正弦波的第j+1个过零点,此时刻为tT2,而信标节点Ri(i=1,2,…,N,假设有N个信标节点)在tR1时刻接收目标节点发射的第j个过零点,在tR2时刻接收到第j+1个过零点,如图1所示,则位置Pj到信标节点i的距离为

图1 目标节点和一个信标节点的信号发射接收时间显示Fig.1 Transmit and receive times of signals between an objective node and a beacon node
(2)
位置Pj+1到信标节点i的距离为
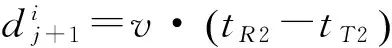
(3)
式(2)-式(3)得:

(4)


1.2 定位模型
设在二维坐标系中,信标节点Ri的坐标为(mi, ni),如图2所示,目标节点从Pj移动至Pj+1.

图2 目标节点运动时相对于某一信标节点的距离Fig.2 Distance between a beacon node andan objective node in motion
由图2可得

(5)
由于测量值为目标节点在不同位置相对于同一信标节点之间的距离差,与目标节点的位置相关,可利用最小二乘法的思想将问题转化为求一组解xj,yj,xj+1,yj+1使得目标函数最小:

(6)
其中,

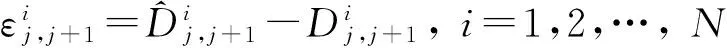
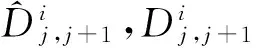
2 迭代定位算法
2.1 起始位置分析
由于每个测量值为目标节点2个位置坐标的函数,由式(5)可推知:
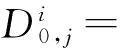
(7)
将每一步得到的D相加便可得到目标节点起始位置与每一步轨迹点间的测量值D.若目标节点起始坐标P0(x0,y0)已知,则根据起始位置与运动位置间的测量值便可优化用算法求得目标运动轨迹[5],因此定位的关键是求起始位置的坐标值.
当求得的起始位置使得目标节点的所有测量点的目标函数之和(式(8))最小时,该起始位置就是起始坐标定位的最优解,即全局最优解.
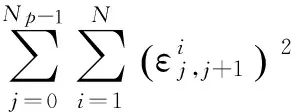
(8)
其中,Np为总测量点数.
由于存在测量误差,每增加一个测量点优化后所得的起始位置可能不同.但随着轨迹测量点数的增多,未知量增多,目标函数最小值优化的计算量增大,同时当计算到一定的基线长度及增加足够的轨迹点数后,起始坐标值受测量误差的影响将降低,其值与理想值间的差距较小,可以作为定位的最优初始位置.
目前,较常用的优化算法主要有梯度法、牛顿迭代法等经典算法以及遗传算法、粒子群算法等智能优化算法.智能算法是一种启发式算法,耗时长,对高维问题求解的正确率较低.为提高定位速度和准确率,本文选用拟牛顿法(BFGS)进行目标优化.拟牛顿算法是一种求解非线性方程最优化问题的方法,克服了牛顿算法计算过程中需要求导、求逆的缺点,将Jacobi矩阵简化为Hk+1=Hk+ΔH,保持了算法的超线性收敛速度[6].但BFGS算法属于局部收敛算法,对初始猜测值的依赖性很强,越接近精确解,其收敛速度越快.
2.2 迭代算法
为了提高定位精度和收敛性,降低初始猜测值对计算结果和收敛性的影响,本文设计了一种基于拟牛顿法的定位迭代算法,其迭代流程如图3所示.
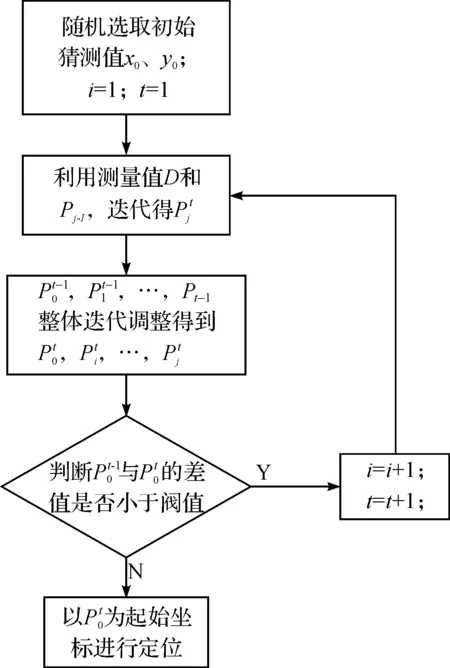
图3 算法流程图Fig.3 Flow chat of algorithm
随着测量值D的增加,每得到一个新的测量位置后即对所有已得坐标位置进行调整.不断将位置信息作为新的信息,使得重新调整后的P0一步步跳出局部解,更靠近理想初值.当调整前后P0的坐标位置变化量小于阈值时,则认为该位置为定位的初始位置解,由该起始位置与运动位置间的测量值采用优化算法求得目标的运动轨迹.
2.3 定位仿真误差分析
为验证定位算法的效果,在Dell-T7500,操作系统为Windows 8,仿真软件Matlab版本为R2013a的环境下,模拟实际现场房间进行仿真.在仿真中假设房间为10 m×8 m的长方形,在其四角放置4个接收器作为信标节点,给节点人为施予噪声量.假设人的行走轨迹分别如图4(a)、(b)所示.取不同轨迹点相对于同一信标节点的距离差D作为测量值,信噪比SNR=10 dB.在长方形内随机选取一对坐标作为初始位置P0的初始猜测值.
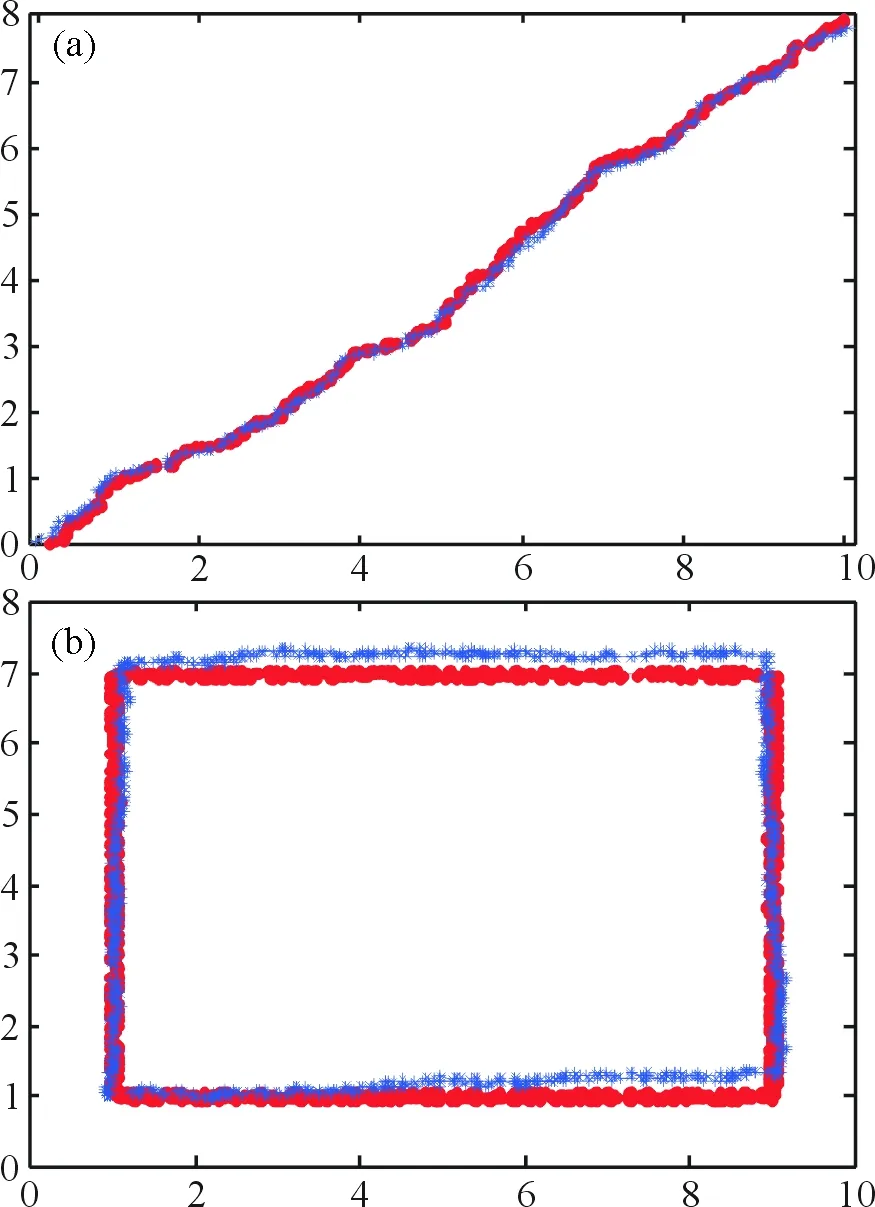
图4 (a)对角路径,(b)闭合路径Fig.4 (a)Diagonal path, (b)closed path
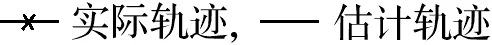
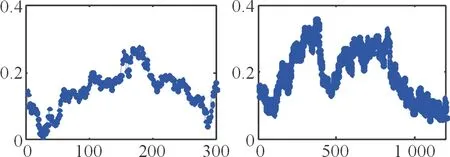
图5 对角路径和闭合路径的定位误差Fig.5 Error of diagonal path location andclosed path location
2.4 初始值分析
由于拟牛顿迭代算法的局部收敛性,对于一般的非二次函数,当选取的初始点比较靠近极小点时,迭代算法可能局部收敛到极小值.为查看随机选取初始猜测值对定位成功的影响,在对角路径中运行迭代100次以求取初始位置P0,测量点数为70.图6中横轴表示测量点数,(a)为随机取初始猜测值运行100次时,初始位置P0的横坐标x0随测量点数的变化;(b)表示同样条件下P0的纵坐标y0随测量点数的变化.

图6 随机选取初始猜测值时,初始位置横纵坐标的收敛情况Fig.6 Convergence of original positions withrandom initial values
由图6可知,初始猜测值的不同会导致初始位置的收敛路径不同,本实验95%收敛到同一位置,即正确初始位置并保持稳定,但也有小部分圈收敛到局部最优.图7展示了初始猜测值的分布,其中纵坐标上三角形表示正确初始位置,小圆圈表示错误的局部收敛的初始猜测值,可见它们与正确的初始位置相距较远.

图7 随机选取的初始猜测值分布图Fig.7 Distribution of random initial values
为解决由初始值错误导致定位不准的问题,参考文献[7]提出采用PSO算法缩小初始位置范围,得到粗略的初始位置x0,y0后,用本文的定位算法经迭代得到稳定初始位置.图8为程序运行100次时初始位置x0,y0的迭代结果,可见引入PSO算法后能准确算得初始位置,且收敛速度加快,在30个测量点时结果已稳定,可用于计算后续轨迹.
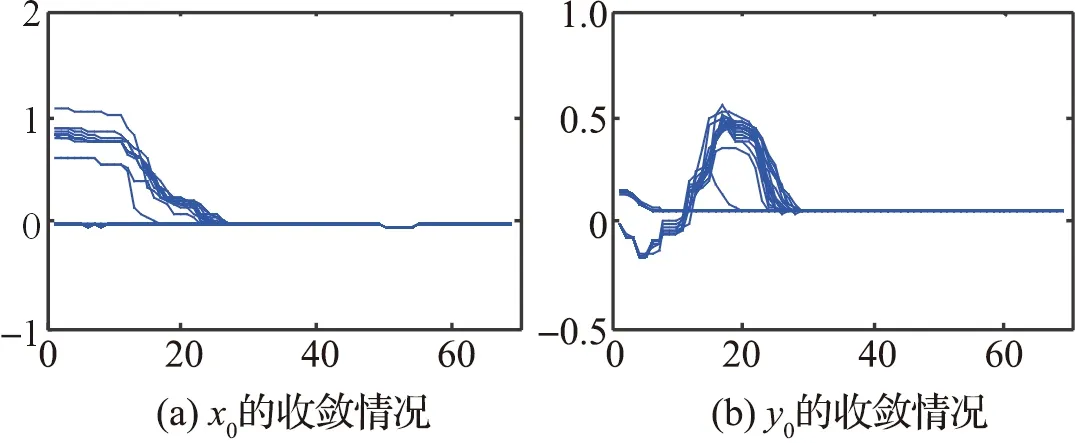
图8 基于PSO算法的初始位置收敛结果Fig.8 Convergence of original positions based on PSO
3 总 结
提出了一种根据多普勒效应测距的新的室内定位方法,基于拟牛顿算法设计了一种随机初始猜测值的初始位置求解方法,将定位问题转化为最小值优化问题.而后采用PSO算法对初始值进行进一步改进.仿真实验表明,该方法定位误差小,成功率较高.该方法为研究固定观测站对运动辐射源的定位应用提供了基础.
[1] 汶晓勇,肖越.GPS和A-GPS技术研讨[J].通信技术,2011(8):76-78. WEN X Y, XIAO Y. Research on GPS and A-GPS technology[J]. Communications Technology,2011(8):76-78.
[2] APARICIO S, PÉREZ J, TARRO P, et al. An indoor location method based on a fusion map using bluetooth and wlan technologies[C]//International Symposium on Distributed Computing and Artificial Intelligence 2008 (DCAI 2008). Berlin/Heidelberg: Springer,2009:702-710.
[3] 陈聪传,程良伦.区域细化的RFID室内定位算法[J].计算机应用与软件,2011,28(1):50-52. CHEN C C, CHENG L L. RFID indoor localization algorithm based on region refinement[J]. Computer Applications and Software,2011,28(1):50-52.
[4] 李炳荣,曲长文,苏峰,等.机载单站无源定位技术分析[J].战术导弹技术,2005(6):35-39. LI B R, QU C W, SU F, et al. Analysis of airborne single station passive location technology[J]. Tactical Missile Technology,2005(6):35-39.
[5] 陆洪涛,马飞.基于多普勒频率差的三站无源定位技术[J].舰船电子对抗,2008,31(1):29-31. LU H T, MA F. Three station passive location technology based on Doppler frequency difference[J]. Shipboard Electronic Countermeasure,2008,31(1):29-31.
[6] YUAN G, LU X. An active set limited memory BFGS algorithm for bound constrained optimization[J]. Applied Mathematical Modelling,2011,35(7):3561-3573.
[7] 魏明生,童敏明,訾斌,等.基于粒子群-拟牛顿混合算法的管道机器人定位[J].仪器仪表学报,2013,33(11):2594-2600. WEI M S, TONG M M, ZI B, et al. Pipeline robot localization based on particle swarm quasi Newton hybrid algorithm[J]. Journal of Instrument and Meter,2013,33(11):2594-2600.
A quasi-Newton indoor localization algorithm based on the Doppler effect.
ZHANG Xiaoyan1, SUN Tingting2, XU Xinmin2
(1.ZhejiangChangzhengVocationalandTechnicalCollege,Hangzhou310023,China; 2.CollegeofInformationandElectronicEngineering,ZhejiangUniversity,Hangzhou310027,China)
To avoid the clock synchronization between objective node and beacon nodes in indoor location system, a new distance measuring method based on the Doppler effect is proposed. A quasi-Newton indoor localization algorithm is implemented for distance measurement. The initial parameters for quasi-Newton are obtained randomly. Quasi-Newton is used to get each single position. Then, all the relative positions would be iterated to adjust the original position for localization. Matlab simulations show that the location error is less than 0.5 m when SNR is 10. Then, particle swarm optimization is applied to improve the performance of convergence.
Doppler effect; quasi-Newton; indoor localization

2016-05-23.
浙江省公益性技术应用研究计划项目(2015C31073).
张晓燕(1983-),ORCID:http://orcid.org/0000-0002-9929-2626,女,硕士,讲师,主要从事嵌入式系统研究.
*通信作者,ORCID: http://orcid.org/0000-0002-0910-2375,E-mail:xuxm@zju.edu.cn.
10.3785/j.issn.1008-9497.2017.03.013
TP 301.6
A
1008-9497(2017)03-322-05
