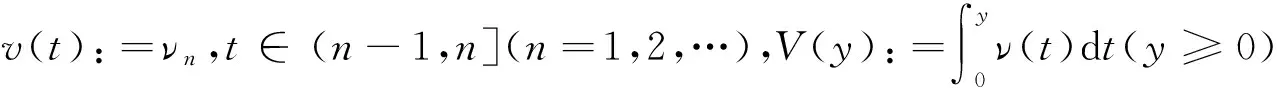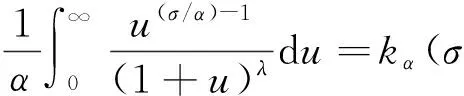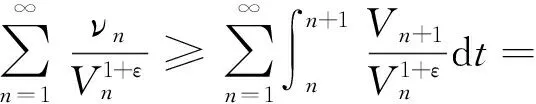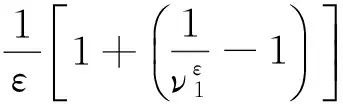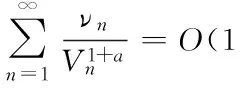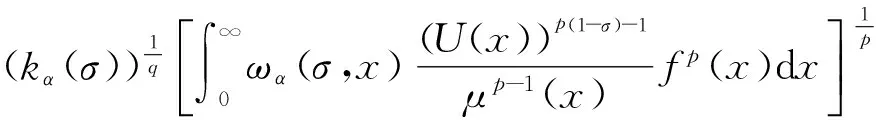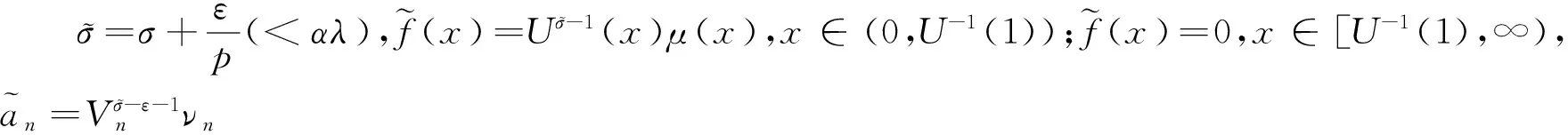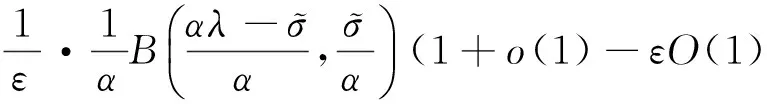一个半离散非齐次核的Hilbert型不等式

2017-05-18杨必成陈强

浙江大学学报（理学版） 2017年3期

关键词：权函数陈强等价

杨必成, 陈强

(1. 广东第二师范学院数学系, 广东广州510303； 2. 广东第二师范学院计算机科学系, 广东广州510303)

一个半离散非齐次核的Hilbert型不等式

杨必成1, 陈强2

(1. 广东第二师范学院数学系, 广东广州510303； 2. 广东第二师范学院计算机科学系, 广东广州510303)

引入独立参数,应用权函数的方法及实分析技巧,建立一个具有最佳常数因子的半离散非齐次核的Hilbert型不等式,还考虑了其具有最佳常数因子的等价形式.

Hilbert型不等式;参数;权函数;等价式;逆式

Journal of Zhejiang University(Science Edition), 2017,44(3):292-295

(1)

(2)

当μi=νi=1(i∈N)时,式(2)变为式(1)(文献[2]并没有证明式(2)及确定常数因子的最佳性).

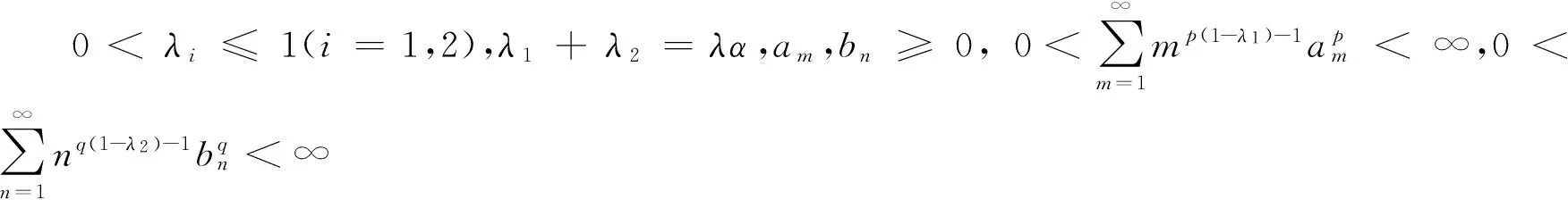
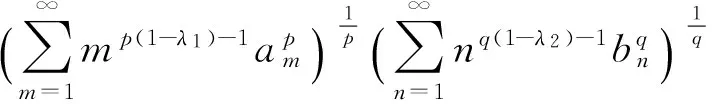
(3)

(4)

(5)

关于半离散Hilbert不等式的一些最新结果,可参阅文献[8-11].

下文引入独立参数,应用权函数法及实分析技巧,建立一个类似于式(5)的具有最佳常数因子的半离散非齐次核Hilbert型式,同时考虑其具有最佳常数因子的等价式.

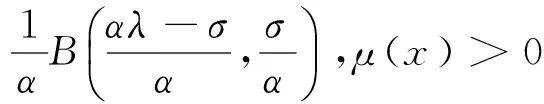
(6)

(7)

则有以下不等式:ωα(σ,x)

(8)

(9)

对上式做变换：u=Uα(x)Vα(t),有

故式(8)成立.

故式(9)成立.证毕.

(10)

故式(10)成立.证毕.

(11)

(13)

证明配方,并由带权的Hölder不等式[12],有

(14)

由式(9)及Lebesgue逐项积分定理[13],有

(15)

再由式(8)，有式(12).配方并由Hölder不等式[12],有

(16)

故式(12)成立,且与式(11)等价.

同理可证式(13)成立,且其与式(11)等价.因而式(11)、(12)与式(13)齐等价.证毕.

(17)

若用正常数K(≤kα(σ))取代式(11)的常数因子kα(σ)后，式(11)仍成立,则有

即有

kα(σ)≤K(ε→0+).

故K=kα(σ)为式(11)的最佳值.

式(12)的常数因子必是最佳值.不然,由式(16),必导出式(11)的常数因子亦非最佳值的矛盾.同理,由等价性,可证式(13)的常数因子为最佳值.证毕.

[1]HARDYGH.NoteonatheoremofHilbertconcerningseriesofpositiveterms[J]. Proceedings London Math Soc,1925,23(2):Records of Proc xlv-xlvi.

[2] HARDY G H, LITTLEWOOD J E, POLYA G. Inequalities[M]. Cambridge: Cambridge University Press,1952.

[3] YANG B C. On best extensions of Hardy-Hilbert’s inequality with two parameters[J]. Journal of Inequalities in Pure and Applied Mathematics,2005,6(3):Article No 81.

[4] 王竹溪,郭敦仁.特殊函数论[M].北京:科学出版社,1979. WANG Z X，GUO D R. Introduction of Particular Functions[M]. Beijing: Science Press,1979.

[5] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009. YANG B C. The Norm of Operator and Hilbert-Type Inequalities[M]. Beijing: Science Press,2009.

[6] YANG B C. Discrete Hilbert-type Inequalities[M]. Sharjah: Bentham Science Publishers,2011.

[7] 杨必成.一个推广的Hardy-Hilbert型不等式[J].广东第二师范学院学报,2015,35(3):1-8. YANG B C. An extension of Hardy-Hilbert-type inequality[J]. Journal of Guangdong University of Education,2015,35(3):1-8.

[8] 杨必成,陈强.一个半离散含多参数的Hilbert型不等式[J].浙江大学学报:理学版,2012,39(6):623-626. YANG B C, CHEN Q. A half-discrete Hilbert-type inequality with multi-parameters[J]. Journal of Zhejiang University: Science Edition,2012,39(6):623-626.

[9] HUANG Q L, WANG A Z, YANG B C. A more accurate half-discrete Hilbert-type inequality with a general non-homogeneous kernel and operator expressions[J]. Mathematical Inequalities and Applications,2014,17(1):367-388.

[10] WANG A Z, YANG B C. A more accurate reverse half-discrete Hilbert-type inequality[J]. Journal of Inequalities and Applications,2015:85.DOI:10.1186/s13660-015-0613-8.

[11] YANG B C, DEBNATH L. Half-Discrete Hilbert-Type Inequalities[M]. Singapore: World Scientific Publishing Co Pte Ltd，2014.

[12] 匡继昌.常用不等式[M].济南:山东科技出版社,2004. KUANG J C. Applied Inequalities[M]. Jinan: Shandong Science and Technology Press,2004.

[13] 匡继昌.实变函数与泛函分析(续论)[M].北京:高等教育出版社,2015. KUANG J C. Real Functions and Functional Analysis (Continuous)[M]. Beijing: Higher Education Press,2015.

A half-discrete Hilbert-type inequality with a non-homogeneous kernel.

YANG Bicheng1，CHEN Qiang2

(1.DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou510303,China；2.DepartmentofComputerScience,GuangdongUniversityofEducation,Guangzhou510303,China)

By introducing independent parameters and applying the method of weight functions and technique of real analysis, a half-discrete Hilbert-type inequality with a non-homogeneous kernel and a best possible constant factor is provided. The equivalent forms with the best possible constant factors are considered.

Hilbert-type inequality; parameter; weight function; equivalent form; reverse