例析对偶式在解三角问题中的妙用

甘肃省永昌县第一高级中学(737200) 张得南●



例析对偶式在解三角问题中的妙用

甘肃省永昌县第一高级中学(737200)
张得南●

在求解或证明一些三角问题时，认真观察题目的结构特征，灵活运用对偶的数学思想，构造出对偶式，并对原式和对偶式进行和、差或积的运算，就能使问题巧妙地解决，起到事半功倍的效果.

一、求值

例1 求sin10°sin30°sin50°sin70°的值.

解 设M=sin10°sin30°sin50°sin70°,

构造对偶式N=cos10°cos30°cos50°cos70°.

则MN=sin10°sin30°sin50°sin70°×cos10°cos30°cos50°cos70°

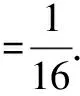
点评 利用倍角公式构造出对偶式，巧妙地降低了运算量.

例2 求sin210°+cos240°+sin10°cos40°的值.

解 设M=sin210°+cos240°+sin10°cos40°,

构造对偶式，

N=cos210°+sin240°+cos10°sin40°.

则M+N=2+sin50°. (1)

M-N=-cos20°+cos80°-sin30°

=-cos(30°-50°)+cos(30°+50°)-sin30°

由(1)+(2)得

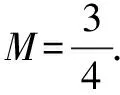
点评 通过题目结构特征的观察，构造和差对偶式，起到了出奇制胜的效果.

二、化简

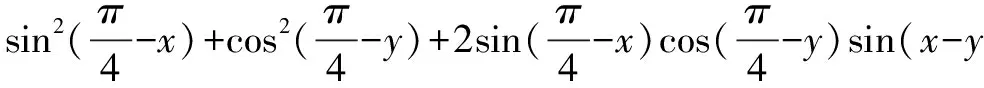
则M+N=2+2sin(y-x)sin(x-y)=2-2sin2(x-y)=2cos2(x-y). (1)

M-N=-sin2x+sin2y+2sin(x-y)cos(x+y)

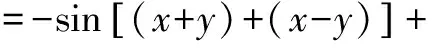
=0. (2)

由(1)+(2)得

2M=2cos2(x-y)，

即M=cos2(x-y).

G632

B

1008-0333(2017)10-0009-02