数学教师专业素养的概念构建及测评
2017-05-17左浩德裴昌根
左浩德 裴昌根
教师教育和发展研究—数学(Teacher Education and Development Study in Mathematics,TEDS-M)是由国际教育成就评价协会(The International Association for the Evaluation of Educational Achievement,IEA)开展的一项评估参与国家或地区职前数学教师教育有效性的大型国际比较研究①赵冬臣、马云鹏:《教师教育国际比较研究的新进展:TEDS-M评介》,《全球教育展望》2010年第12期,第60-64页。,其收集了来自不同国家和地区的数学教师专业知识和专业信念的数据并对其进行比较分析。该研究历时3年(从2007年到2009年),共有23000名来自东西方15个国家和1个地区(中国台湾)的职前数学教师(处于数学教师培养计划最后一年的职前数学教师)参与了这一研究。该研究从样本的选取、数据收集、数据编码和数据分析均按照IEA 的标准执行,有效地保证了研究的信效度。该研究在参考了以往相关研究的基础上构建了数学教师专业素养的概念框架和测评体系,有力地推动了数学教师教育研究的向前发展。
一、TEDS-M中数学教师专业素养的概念框架
TEDS-M研究的主要研究问题是小学和初中的职前数学教师具备怎样的数学知识以及与教学相关的知识,来自不同国家或地区的职前数学教师所具备的知识有什么区别。为了评估各国数学教师教育的有效程度,TEDS-M研究构建了数学教师专业素养这一概念框架(见图1),并把数学教师专业素养的养成作为数学教师教育的核心目标。
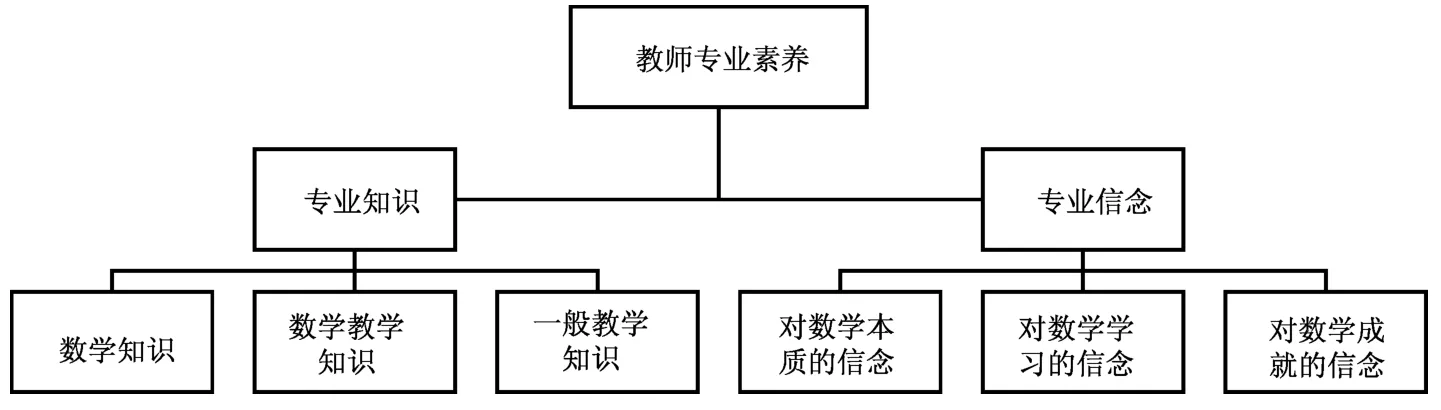
图1 数学教师专业素养概念框架
教师的工作包含多个方面,但课堂教学无疑是教师工作的核心,因此培养和提升教师的课堂教学能力已经成为众多国家数学教师教育的首要目标①Kaiser G,Busse A,Hoth J,et al.About the Complexities of Video-Based Assessments:Theoretical and Methodological Approaches to Overcoming Shortcomings of Research on Teachers' Competence.International Journal of Science and Mathematics Education,2015,13(2):369-387.。TEDS-M研究认为数学教师的课堂教学能力主要受其专业素养的影响,所以其将研究的重心放在了职前数学教师的专业素养,并认为数学教师的专业素养包含两大要素:教师的专业知识和教师的专业信念。在这一概念框架下,数学教师的专业素养成为TEDS-M研究中最为重要的研究变量。数学教师的专业素养被认为是影响教师课堂教学的关键变量。
TEDS-M研究构建的数学教师专业素养概念框架是在对已有研究进行整合和再创造的基础上产生的。该研究中提出的数学教师专业素养的概念框架以教师的课堂教学能力为出发点,将影响数学教师课堂教学的多个因素进行了整合,突出了教师专业发展中的两个核心变量——教师的专业知识和教师的专业信念。聚焦数学教师专业素养,探究数学教师的专业知识和专业信念,解决了当前数学教师教育领域内急需解决而又意义重大的研究问题。当然,这一框架也具有一定的局限:一方面该概念框架只是包含了与教学相关的内容,对教师其他方面的专业素养并未考虑。由于教师工作涉及面广,仅仅胜任教学工作未必就意味着能够成为一名优秀的教师;另一方面,这个概念框架虽考虑了不同文化背景下的数学教师专业素养的共同点,但对文化间的差异性并未顾及。在不同文化背景下,数学教师的专业素养要求可能不同,因而数学教师的专业素养内涵也可能会有差异。但是,不管怎样,该概念框架的提出为以后的研究打下了坚实的基础。以下首先对数学教师专业素养概念框架中的各组成部分进行具体的评介,然后再对相应的测评手段进行介绍并举例说明。
二、TEDS-M中数学教师专业知识的概念框架及测评
(一)数学教师专业知识的概念框架
美国学者舒尔曼在1985年美国教育研究协会年会的报告中最先提出强调学科教学知识的教师知识理论②Shulman L S.Those Who Understand:Knowledge Growth in Teaching.Educational Researcher,1986,15(2):4-14.。三十年来,舒尔曼的教师知识理论得到了广泛应用并不断完善,TEDS-M研究根据舒尔曼的理论将数学教师的专业知识划分为数学内容知识、数学教学知识和一般教学知识三个二级维度(见表1)。

表1 数学教师专业知识的概念框架
在TEDS-M研究中,数学内容知识的定义是教学中用到的数学知识,其被按照内容和认知两个方面进行了进一步的划分。对于数学教学知识,TEDS-M研究将其划分为数学课程知识、备课时所需的知识和上课时所需的知识。一般教学知识则是管理班级的知识等不涉及具体学科内容教学的教育教学知识。不难发现,以上的教师专业知识概念框架不同于一般的教师知识框架,其没有将教师的各种知识进行碎片化的划分。TEDSM研究建立教师专业知识概念框架的目的是为了设计教师专业知识的评价工具。这样的分类虽显笼统,但也具有显而易见的优势:不会被细分的教师知识框架所局限,花费大量的篇幅去定义和区别教师的各种不同的细节知识。
数学内容知识方面,TEDS-M研究将数学内容知识按照内容属性划分为:数与符号、代数与函数、几何与测量以及数据和概率。此外,TEDS-M研究还将数学内容知识根据掌握要求分为了解、运用和论证三个认知水平。TEDS-M研究对内容和认知上的分类框架沿用了国际数学与科学趋势研究(Trends in International Mathematics and Science Study,TIMSS)中的数学学科内容分析框架。虽然TIMSS研究中的数学内容分析框架是为测试学生数学知识掌握水平设计的,但是TEDS-M的研究人员认为教师和学生所具备的数学知识只是在深度和广度上有所不同,而在内容属性和认知水平上基本相同。因此,TEDS-M研究沿用了TIMSS 中对数学知识内容的分类框架。
数学教学知识方面,TEDS-M研究一方面遵从了舒尔曼学科教学知识定义中的两个核心要素:选取教学策略的知识和识别学生最可能犯的错误的知识,另一方面又从评价工具设计的角度将教师的学科教学知识分为:(1)教师整体上的课程知识,包括了解学生整个学习生涯中的全部数学课程,熟悉评价标准从而能够识别教学内容中的重难点以及课程内容与其他领域知识的联系等;(2)备课中所运用的知识,包括预设学生可能的典型回答,选择合适的例子和比喻去授课等;(3)授课中所运用的知识,包括在课堂上回应意料之外的学生的提问,辨别学生的某些非典型错误的根源等。
对于一般教学知识来说,舒尔曼认为它应该包括有助于教师传授学科知识的班级管理和组织的广泛的原则和策略①Shulman L S.Knowledge and Teaching:Foundations of the New Reform.Harvard Educational Review,1987,57(1):1-23.。对此,有其他学者认为一般教学知识包括了学习和教学的一般策略、对不同教育思想的理解、对学习者的一般认识以及班级管理的技术②Grossman P L,Richert A E.Unacknowledged knowledge growth:A re-examination of the effects of teacher education.Teaching & Teacher Education,1988,4(88):53-62.。虽然一般教学知识的定义略显宽泛,但它却是教师知识体系的一个重要的补充。学科知识和学科教学知识一般需要涉及具体的教学内容,相对而言,一般教学知识通常不涉及具体的学科教学内容。
(二)数学教师专业知识测试题
编制教师专业知识的测试题是一项系统性的工作。测试题不仅需要具备很高的信效度,同时题意还要简洁准确,从而保证不会随翻译语言的不同而改变题目本意。TEDS-M研究中的教师专业知识测试题大部分来源于国际教师知识比较研究(Mathematics Teaching in the 21stCentury,MT21)和密歇根州立大学的“ Knowing Mathematics for Teaching Algebra,KAT”研究项目以及密歇根大学的“Learning Mathematics for Teaching,LMT”研究项目①②Tatto M T,Schwille J,Senk S L,et al.Policy,Practice,and Readiness to Teach Primary and Secondary Mathematics in 17 Countries.2012.。
(1)“一带一路”沿线各国物流绩效水平的改善会拓宽中国机械运输设备出口的种类,增加中国机械运输设备出口的数量,提高中国机械运输设备出口的价格。毫无疑问,无论种类、数量还是价格都有利于中国机械运输设备出口总量的增长。因此,中国应该积极推进与 “一带一路”沿线各国的基础设施投资合作,改善贸易伙伴国的物流绩效水平,与 “一带一路”沿线各国实现设施联通、贸易畅通。
1.数学内容知识测试题的编制
TEDS-M研究中的测试题目所包含的数学内容知识大部分高于被试教师所要教学的年级的内容知识。具体的难度划分是:初级难度——教师今后要教学年级的内容;中级难度——高于教师今后所教学年级一到二个年级的内容;高级难度——高于教师今后所要教学年级三个年级或者以上的内容。在数学内容知识的小题中,数与符号、代数与函数、几何与测量的题目各占30%,还有10%的数据和概率的题目。试卷中有单选题、复选题和解答题三种题型。以下选取一些典型题目进行分析。

例题1是测试职前小学数学教师的数学内容知识掌握水平。解决这道题目不仅需要初中平行四边形部分的有关知识,还需要高中集合部分韦恩图的知识。因此对于职前小学教师来说,此题涉及的知识高于他们所要教的年级的内容知识。在内容维度上,该题属于几何知识领域;在认知维度上,此题属于了解水平。题型是单选题。此题难度不高,但研究结果表明③Tatto M T,Schwille J,Senk S L,et al.Policy,Practice,and Readiness to Teach Primary and Secondary Mathematics in 17 Countries.2012.只有61%参与调查的教师给出了正确的解答,相对于此题的难度来说,正确率偏低。
对于职前初中数学教师而言,考察的内容涉及初中、高中和大学内容,例如:

例题2以矩阵为背景,类比矩阵的乘法定义了一种新运算并考察了教师零矩阵的概念。矩阵属于高中或者大学内容,内容上属于代数范畴。此题是解答题,要求教师首先判断论述的正误并说明道理,认知维度上属于论证。该题代表TEDS-M研究测试中难度较高的题目,研究结果显示④Tatto M T,Schwille J,Senk S L,et al.Policy,Practice,and Readiness to Teach Primary and Secondary Mathematics in 17 Countries.2012.仅有2%的参与教师做出完全正确的回答,19%的教师做出了部分正确的回答。对于没有数学专业背景的职前初中数学教师来说,找出该题的反例确属不易,但对于那些拥有数学专业背景的教师来说,高等代数中矩阵部分的知识有助于他们解决该题。
以上两题考察了职前数学教师的数学内容知识,出题素材高于教师将要教学的年级,内容和认知要求与教师专业知识概念框架相吻合。
2.学科教学知识测试题的编制
学科教学知识是一种与情境紧密联系的知识,它需要结合特定的教学内容或者教学情境进行设计①Depaepe F,Verschaffel L,Kelchtermans G.Pedagogical content knowledge:A systematic review of the way in which the concept has pervaded mathematics educational research.Teaching and Teacher Education,2013,34:12-25.。因此在TEDS-M研究中学科教学知识的试题都是设定在具体的教学情境中以考查教师对相关知识之间的联系的熟悉程度、课堂的准备程度(选取的比喻是否恰当,能否找到学生错误的根源等)以及对学生非典型的错误或者提出的意料之外的问题做出快速回应等,例如:

3.一般教学知识测试题的编制
学科内容知识和学科教学知识的试题需要结合具体的数学内容,而一般教学知识的测试题通常不落实在具体的数学知识点上,例如:

例题4旨在考查教师常规备课知识,虽然问的是对他人备课所提出的建议,其实反映了该教师对自己备课经验的总结反思。研究发现③Tatto M T,Schwille J,Senk S L,et al.Policy,Practice,and Readiness to Teach Primary and Secondary Mathematics in 17 Countries.2012.大部分教师给出的回答是“你的教学目标是什么?”“你的学生之前有没有具备足够的预备知识?”以及“学生是小组讨论还是独立思考?”等等,注意到这个问题中不涉及具体的教学内容,属于一般教学知识的范畴。
TEDS-M在教师测试题库的建立上花费了大量的精力,出于版权等原因,IEA 只公布了约25%的例题供参考。以上分析的例题均来自于其公布的试题。此外,TEDS-M作为大型教育的测评项目,它采用了大尺度教育测评量化设计和方法进行数据收集和测试题的数据分析,例如采用矩阵取样技术(Matrix-Sampling)、似真值量表化方法(Plausible values scaling)等,从而确保其能够向各国政府以及公众传达具有影响力的结论。
当然,TEDS-M研究在教师知识的测评试题设计上也存在着一定的问题。首先是内容分布不均,大部分题目集中在数与符号、代数与函数、几何与测量这些内容,数据和概率部分涉及不足。其次在题型设计上,大部分题目(尤其是关于数学学科教学知识)结合了具体的教学情境,但也增加了教师的阅读负担。另外,题型设置多为选择题,某些被试者可以从选项的描述中推测出正确答案,这在一定程度上也影响了试题的效度。
三、TEDS-M中数学教师专业信念的概念框架及测评
(一)数学教师专业信念的概念框架
除了教师的专业知识外,教师的专业信念也对教师的课堂教学有较大的影响①Richardson V.The Role of Attitudes and Beliefs in Learning to Teach.In:Sikula J.Handbook of Research onTeacher Education.New York:Simon & Schuster,1996.。“虽然国际上还没有对好的教学形成共识,但却没有人否认教师对数学本质的理解对形成好的教学有着很大的作用。”②Thompson A G:Teachers' beliefs and conceptions:A synthesis of the research,Handbook of research on mathematics teaching and learning:A project of the National Council of Teachers of Mathematics,New York,NY,England:Macmillan Publishing Co,Inc,1992:127-146.教师的专业信念对教师教学的影响是潜移默化的。研究表明③Staub F C,Stern E.The nature of teachers‘ pedagogical content beliefs matters for students' achievement gains:Quasi-experimental evidence from elementary mathematics.Journal of educational psychology,2002,94(2):344.,致力于培养学生学习兴趣的教师和致力于培养学生解题能力的教师在教学上有很大的差异。因此TEDS-M研究将数学教师的专业信念视为影响数学教师教学的一个重要变量,并进一步将其划分为教师对数学本质、数学学习以及对数学成就三个方面的专业信念。教师专业信念的概念框架主要来自于密歇根州立大学的Teaching and Learning to Teach Study(TLTS)研究项目。TEDS-M研究中④Tatto M T,Schwille J,Senk S L,et al.Teacher Education and Development Study in Mathematics(TEDS-M):Policy,practice,and readiness to teach primary and secondary mathematics.Conceptual framework.East Lansing:MI:Teacher Education and Development International Study Center,College of Education,Michigan State University,2008.,教师对数学本质的专业信念被分为两类:数学是一系列规则和程序的集合,数学是一个探索的过程。一系列规则和程序的集合强调数学中较多的是静态的概念公式定理等,数学是一个熟能生巧的过程,解决数学的问题需要遵循固有的步骤。而如果把数学看成是一个探索的过程则认为数学中需要创造力,在数学中能够通过探索解决大部分数学问题。教师对数学学习的专业信念则分为学好数学需要遵循教师的指导或通过学生自己的积极探究也能学好数学。教师对数学成就的专业信念则主要探寻教师是否赞同人的数学能力是天生的。
(二)数学教师专业信念的量表
信念是人们对某一类事物总的认识⑤金美月、郭艳敏等:《数学教师信念研究综述》,《数学教育学报》2009年第1期,第25-30页。,因而测量信念适合使用自我陈述式量表进行测量。TEDS-M研究中对数学教师专业信念编制了专门的量表进行测量(见表2)。该量表依据构建在Richardson 和Thompson 对教师信念以及数学教师信念的研究基础上⑥Tatto M T,Schwille J,Senk S L,et al.Policy,Practice,and Readiness to Teach Primary and Secondary Mathematics in 17 Countries.2012.。量表以数学教师专业信念为一级指标,以教师对数学本质的信念、对数学学习的信念、对数学成就的信念为三个二级量表。教师对数学本质的专业信念的题目围绕数学是静态的知识集合还是动态的探索过程。教师对数学学习的专业信念的题目关注两种学习数学的方法的认识:教师指导和学生的自我探究。教师对数学成就的专业信念的题目围绕是否每个人都具备学习数学的能力。量表采用李克特六点量表的形式设置选项,包括非常不同意、不同意、有点不同意、有点同意、同意和非常同意等。
相较于数学教师专业知识的研究而言,数学教师专业信念的研究近年来才逐渐受到关注和重视。TEDS-M研究提出的数学教师专业信念概念框架和研发的相关量表为这方面的研究打下了基础。不难看出,TEDS-M研究中对数学教师专业信念的分类和界定与之前的相关研究不谋而合。首先,就数学本质的信念而言,TEDS-M研究测量的有关数学本质的两种信念分别体现了绝对主义和谬误主义的数学观①胡典顺:《数学观的嬗变及其对数学教育的启示》,《天津师范大学学报》(基础教育版)2012年第2期,第6-10页。。具体来说,TEDS-M研究中测量的数学是“一系列规则和程序的集合”的数学信念体现了绝对主义的数学观,其认为数学是由确定的真理组成的。而另一种测量的数学是“一个探索的过程”的信念符合谬误主义的数学观,其认为数学是可误的,可以通过大胆猜想、批判和反驳发展起来。其次,就数学学习的信念来看,TEDS-M研究测量的“学好数学需要遵循教师的指导”的信念反映了传统教师中心的学习观,其认为教师是课堂的主宰,学生应该绝对服从教师的安排。而“通过自主探究也能学好数学”的信念体现了以学生为中心的学习信念,其认为学生可以积极主动地参与到学习过程之中,根据自身实践学习数学。最后,就数学成就的信念而言,TEDS-M研究测量的“数学是一种天生的能力”的信念反映了教育理念中的先天决定论,其强调人的生物或生理属性对数学学习成就的决定作用,这与重视后天培养的教育观相左。总之,TEDS-M研究中的数学教师专业信念包括了涉及数学教师的主要专业信念,将这些专业信念同时纳入研究框架,有助于发现他们之间的内在联系,从而加深人们对数学教师专业信念的认识。
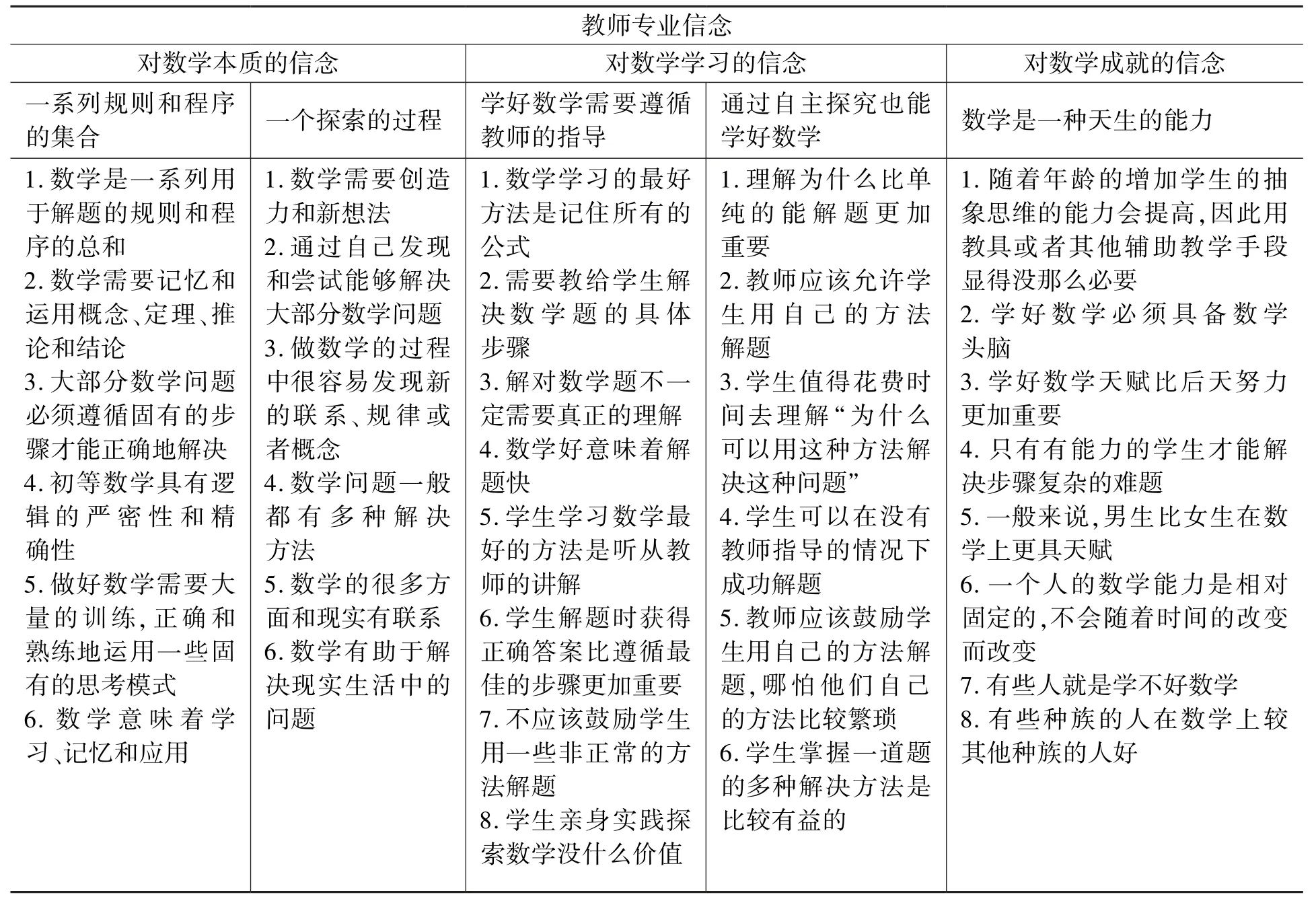
表2 数学教师专业信念量表
四、讨论
TEDS-M研究是首次大型的国际数学教师教育的比较研究,其突出的贡献之一就是构建了数学教师的专业素养框架和与之对应的数学教师专业素养测评体系。该框架在梳理了数学教师的专业知识和专业信念已有研究的基础上,对相关的概念进行了梳理和定义,并且将数学教师的专业知识和专业信念定义为数学教师的专业素养①Gabriele Kaiser S B,Andreas Busse,Martina Döhrmann,Johannes König.Professional knowledge of(prospective)mathematics teachers-its structure and development.the 38th Conference of the International Group for the Psychology of Mathematics Education and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education,2013.。根据这一框架设计的数学教师专业素养的测评体系符合IEA 中严格的信效度要求并经过16个国家和地区的大样本实证检验,因此这一概念框架以及测评体系为今后的类似研究奠定了坚实的基础。当然其也存在着诸如题目内容和题型分布不均、选项设计过于简单之类等问题②③鲍银霞:《TEDS-M对数学教学知识评价工具的研制及启示》,《课程教学研究》2013年第3期,第28-32页。。
TEDS-M研究在对相关核心概念进行深入学理性分析的基础上建立了数学教师专业素养的概念框架并制定了科学的测评体系。根据我国国情,在以后相关的教师教育研究中,可在TEDS-M数学教师的专业素养概念框架和测评体系的基础上加以改进,并应充分考虑如下问题:
(一)中国教师与其他国家教师知识结构的差异
研究表明④曹一鸣、郭衎:《中美教师数学教学知识比较研究》,《比较教育研究》2015年第2期,第108-112页。,中国教师和美国教师在知识结构方面存在较大的差异。例如,中国的教师还需具备一定的教学科研的知识和能力。中国已经建立起比较完善系统的教学研究体系,而且历来重视和鼓励教师集体研究教学问题,所以教研知识和能力是中国教师知识结构的重要组成部分。此外,受考试文化的影响,中国教师对考试的分析能力和对学生应试的指导能力也是教师知识结构中不可忽视的部分。导致这些差异的原因可能是不同文化下对教师专业知识要求所造成的。因此在设计具体教师专业素养测评试题的时候应充分考虑这些差异,并做出相应的调整。
(二)既要注意知识之间的区别也要注意它们之间的联系
TEDS-M的数学教师专业素养概念框架中,对教师的专业知识进行了划分,这样的处理有利于研究者和实践者对教师的专业知识有一个清楚的认识。但是,人们应该意识到这样的划分并不是说明这些知识之间是相互独立的,相反人们应该注意它们之间既有重合也有联系。在具体的试题编制时,可对内容知识和学科教学知识进行区分,但也无需过分划清二者的界限。在解决或处理某些数学问题的过程中,实际上教师的内容知识和学科教学知识都会涉及到,对于此类题目的归类以涉及的最主要的知识进行判定。
(三)职前和在职的教师专业素养测评的重心应有不同
TEDS-M研究的目标对象是职前数学教师,对这一群体的教师而言,它们缺乏教学实践经验,在学科教学知识和一般教学知识上积累不够,因此在设置教师的专业知识的试题比例时,应加重对职前教师的学科内容知识的测评。而对于在职教师的专业知识测评,这一群体已经积累了相当丰富的教学经验,因此对他们专业知识的测评,应该三类知识并重。对要研究的目标教师群体的准确定位,有利于设计出更加精准和有效的教师专业素养测评体系。
(四)兼顾显性和隐性教师专业素养的测评
传统的教师专业素养测评常常关注于教师显性的教学能力,如教师的学科内容知识或者课堂教学能力,而忽视对教师的专业信念这些难以直接观察的教师专业素养进行测评。相关研究指出教师的专业信念对教师的教学有着显著的影响⑤Richardson V.The Role of Attitudes and Beliefs in Learning to Teach.In:Sikula J.Handbook of Research onTeacher Education.New York:Simon & Schuster,1996.。对隐性的教师专业素养的关注和研究,不仅是为了构建一个全面系统的教师专业素养测评体系,而且能更深入地把握教师专业素养发展的因素,从而更有效地促进教师专业素养的养成。因而,在今后的研究中教师的专业信念等隐性的专业素养也应得到重视并且纳入测评体系中。
教师教育是当前国内外教育研究中的热点和难点问题。TEDS-M研究对数学教师的专业素养构建了清晰的概念框架和可信的测评体系,这一研究不仅能够帮助我们汲取国际上最新的研究方法和成果,也能够有助于使国内的研究与国际接轨,从而提升我国的数学教师教育的研究水平和实践效果。
