初中数学教师与学生认知一致性的调查研究
2017-05-17张景斌
张景斌 郝 婕
一、一致性研究概述
统计学中一致性是指当样本容量逐渐增大时,估计值与参数真值几乎完全一致①马戈:《概率论与数理统计》,北京:国防工业出版社,2007年版第134页。。从图形上看,一致性指校准曲线接近规定特性曲线时的吻合程度。无论针对什么对象,一致性(alignment)描述的都是一种吻合或匹配的程度。
教育是一个庞大的系统,由各种要素组成,教育系统内部各要素的吻合或匹配对教师教学及学生学习具有积极的促进作用②Sri Ananda.Rethinking Issues of Alignment under “No Child Left Behind”.WestEd,San Francisco,CA.2003.。教育中一致性的思想萌芽于新行为主义处于鼎盛时期的20世纪60年代初③Cohen,S.A.Implications of Instructional Psychological Research on Mastery Learning Outcomes.A Quarterly Newsletter of the Network of Outcome-Based Schools,1984a(2):18-25.。国内外学者在关注一致性概念研究的同时,对研究路径和研究方法进行了较为广泛的探索。
(一)国外教育一致性研究
关于一致性的研究路径,Webb 提出了横向一致性(horizontal alignment)和纵向一致性(vertical alignment)的研究路径,前者主要研究教育评价与课程标准的一致性,后者研究教育目的、政策、实践等要素之间的一致性①Webb,N.L.Criteria for Alignment of Expectations and Assessments in Mathematics and Science Education.Council of Chief State School Officers,Washington,DC,1997.。Leitzel 认为课程一致性可以通过三条路径来分析:计划和传授之间的一致性、传授和评价之间的一致性以及计划和评价之间的一致性,同样为一致性研究提供了方向②Leitzel,T.C.Platform Unity/Alignment between Course Planning and Testing Decisions in Criterion-Referenced Situation.Virginia Polytechnic Institute and State University,1993.Webb,N.L.Criteria for Alignment of Expectations and Assessments in Mathematics and Science Education.Council of Chief State School Officers,Washington,DC,1997.。
关于一致性的研究方法,主要集中在课程标准与学业评价的一致性测量,并相继出现了一些测量方法。其中影响较大的有三种模式:Webb模式是从知识种类、知识深度、知识广度以及知识分布平衡性四个维度对课程标准和学业评价做一致性判断③Webb,N.L.Criteria for Alignment of Expectations and Assessments in Mathematics and Science Education.Council of Chief State School Officers,Washington,DC,1997.;SEC(Surveys of Enacted Curriculum)模式主要是通过构建二维描述矩阵和内容地图的方式分析一致性水平④Porter,A.C.How SEC Meaures Aligment.Educatioal Researcher,2002(10):4-6.;Achieve 模式将一致性研究维度分为内容中心、表现中心、挑战、平衡和范围⑤范立双、刘学智:《美国“成功分析模式”的诠释与启示》,《比较教育研究》2010年第8期,第77-80页。。
关于教育问题的一致性研究主要集中在以下几个方面:
其一,教学过程与教学评价的一致性研究,是针对实际的课堂教学内容、教师教学行为等与学生学业成就的一致性研究。Cohen 的研究⑥Cohen S A.Instructional Alignment:Searching for a Magic Bullet.Educational Researcher,1987(11),16-19.与Mitchell 的研究⑦Mitchell,F M.The Effects of Curriculum Alignment on the Mathematics Achievement of Third-Grade Students as Measured by the Iowa Test of Basic Skills:Implications for Educational Administrators.Clark University,1998.得到了相似的成果,即如果课堂教学与评价一致性高,那么学生都能够取得相对好的成绩。Gamoran 等人对中学数学课程内容和学生学习成绩进行的研究表明,教师所教授的课程与学生评价结果有着非常高的一致性水平⑧Gamoran,A,Porter,A.C,Smithson,J.,and White P.A.Upgrading High School Mathematics Instruction:Improving Learning Opportunities for Low-Achieving,Low-Income youth.Educational Evaluation and Policy Analysis,1997,19(4),325-338.。Polikoff 就改善教学一致性的研究方法提出,比采取现有分析更有用的方法是及时收集教师教学的自我报告内容作为分析数据,以避免教师对课程标准或“一致性”本身理解的假设⑨Polikoff,M.S.Instructional Alignment under No Child Left Behind.Chicago Journals,may 2012,341-368.。
其二,课程标准与学业评价的一致性研究,反映了教学预期与教学结果的吻合程度。美国课程与评价一致性分析协会指出,“评价应当与课程标准相一致,且应当基于课程标准提供关于学生学业成功的、持续的、一致的信息,应当把评价、课程与教学的一致性作为州、社区、学校努力实现有挑战性课程标准的一项关键性指标”。⑩U.S.Congress.House of Representative Improving Americans Schools Act.Washington DG:U.S.Government Printing Office,1994.转引自刘学智、张雷:《学业评价与课程标准的一致性:韦伯模式本土化探究》,《外国教育研究》2009年第12期,第13-17页。随后,美国出现了许多课程标准与学业评价一致性的研究。例如,Webb 关于三个州数学标准与评价的一致性分析⑪Webb,N.L.Criteria for Alignment of Expectations and Assessments in Mathematics and Science Education.Council of Chief State School Officers,Washington,DC,1997.、Polikoff 关于学业评价与州内容标准的一致性研究⑫Polikoff,M.S.,Porter,A.C.,Smithson,J.How Well Aligned are State Assessments of Student Achievement with State Content Standards.American Educational Research Journal,2011,48(4):965-995.等。Squires 关注了讲授的课程、测试的课程、文本的课程三者之间一致性的研究,指出学区可以通过调整这三类课程提高学生的成绩①Squires,D.Curriculum Alignment Research Suggests That Alignment Can Improve Student Achievement .The Clearing House:A Journal of Educational Strategies,Issues and Ideas,May 2012,129-135.。
其三,教科书与学业成就的一致性、教科书与课程标准的一致性研究。如Price-Baugh 对教科书中若干因素与学生学业水平一致性进行了研究,结果表明除教科书中练习项目的位置这一变量外,学生的学业水平与其所考虑的教科书中所有其他内容变量都有较高的一致性②Price-Baugh,R.Correlation of Textbook Alignment with Student Achievement Scores.http://sunzi.lib.hku.hk/ER/detail/hkul/2988789.。Polikoff 等人针对如何依据核心课程标准以及降低教科书评价成本,对适当简化采用SEC 方法评价教科书与课程标准间的一致性进行了研究③Polikoff,M.S.,Zhou,N.,and Campbell,S.E.Methodological Choices in the Content Analysis of Textbooks for Measuring Alignment With Standards,Educational Measurement,2015,34(3),10-17.。
其四,学生能力与数学教学的一致性研究。一项针对美国K年级(学前班)数学教学内容与学生已有数学知识与能力之间一致性的研究指出,教师对于儿童已经掌握的数学知识与技能了解的信息相对较少,会将教学定位于教师感觉学生已经掌握的内容或已有能力的基础上,结果导致学生能力与数学教学内容之间的不匹配。该研究还发现,儿童入学时的数学能力决定了他们接触的数学内容与随后的数学成绩之间的关系④Engel,M.,Claessens,A.,Finch,M.Teaching Students What They Already Know?The(mis)alignment between mathematics instructional content and student knowledge in kindergarten.Educational Evaluation and Policy Analysis,2013,35(2),157-178.。另有研究结果表明:教师受教育的程度、教师的教学经验与教学一致性呈正相关,但这种关系是非线性的⑤Polikoff,M.S.Teacher Education,Experience,and the Practice of Aligned Instruction.Journal of Teacher Education,2013,64(3),212-225.。
(二)国内教育一致性研究
国内关于一致性的研究起步较晚,研究成果于近几年开始呈现。
关于一致性测量的研究,国内学者主要对韦伯模式、SEC 模式和成功模式等进行研究并运用于本土化问题的分析。也有研究者尝试运用了其他方法,如方全波根据调研所得评价要点,构建了一致性评价指南,再根据指南进行一致性的判断分析⑥方全波:《物理教学设计与新课程标准一致性个案研究》,东北师范大学硕士论文,2010年。;刘思构建了由教学意识和教学行为为坐标轴的直角坐标系,通过调研数据对应点的象限分布分析二者的一致性⑦刘思:《高中数学教师教学意识与教学行为一致性的研究》,东北师范大学硕士论文,2011年。。
从所呈现的研究成果来看,课程标准与学业评价的一致性是研究的重点,且学业评价集中在中考和高考两类评价。例如,罗莹等运用SEC 模式分析了2010年我国18个省市的中考物理试卷与课程标准之间的一致性水平⑧罗莹、王宏博、张薇薇、希望:《2010年中考物理试卷与课程标准的一致性分析》,《基础教育课程》2011年第3期,第70-75页。。王磊等运用SEC 模式研究了九个省市的中考化学试题与课程标准的一致性水平⑨王磊、黄琼、刘东方:《中考命题与化学课程标准的一致性研究——基于九省市中等学校招生考试概念原理知识的比较》,《基础教育课程》2010年第3期,第75-80页。。刘恩山等运用SEC 模式研究了海南、广东、山东和宁夏四个首批进入新课程实验区的省份2010年生物高考试卷与课程标准的一致性⑩刘恩山、卢群、张颖之:《2010年高考生物试卷与课程标准一致性分析》,《 基础教育课程》2010年第9期,第61-67页。。朱行健等运用韦伯模式与逻辑分析法对新课程物理高考考试大纲与课程标准进行了匹配性分析⑪朱行健、李勇:《新课程物理高考考试大纲与课程标准的匹配性研究》,《课程·教材·教法》2007年第10期,第56-59页。。
(三)简要评述
总体而言,教育领域的一致性研究,关注了教育要素之间的匹配程度,对教育发展起到了很好的引导作用。一致性研究方法的探寻虽然取得了可喜进展,但这些方法还在完善中,运用这些方法可以研究的问题还很有限。绝大多数一致性研究都集中在课程标准、教学内容等与学业评价的一致性上,关于教师的教学信念、教师对学生的认知等因素与学生学习相关因素的一致性研究则很少,但这些都是影响教学一致性的直接的或潜在的重要因素。究其原因,一方面是由于学业评价与课程标准、教学内容的一致性是课程评价领域的热点问题。另一方面,相对于其他教育要素之间的一致性测量,课程标准、教学内容与学业评价之间的一致性比较容易进行量化分析,测量工具较为成熟。而教师与学生的认知一致性及其对学生学业成绩影响的研究,则对研究者提出了更高的挑战。
我国的一致性研究刚刚起步,无论研究方法还是研究内容都深受国外研究经验的影响。研究方法方面基本处于移植性使用阶段,缺少本土化的、创新性的一致性分析模式的构建,研究内容方面与国外研究相比单一性更加突出。然而,教育的问题是复杂的,对于其他要素之间的一致性研究也至关重要。本研究既是对研究内容也是对研究方法的新的尝试。
二、研究设计与实施
(一)研究内容
学生的数学认知水平是数学教学的重要依据之一。教师对学生数学认知的认知水平越高,则越能很好地把握学生的数学学习规律,实施高质量的数学教学。本文所研究的内容是初中数学教师对学生数学认知水平的认知与学生实际数学认知水平的一致性,即二者的吻合程度。本文在不引起歧义的情况下也简称之为教师的一致性水平。
(二)研究思路
无论是研究课程标准与学生学业评价之间的一致性,还是研究教科书或习题与课程标准之间的一致性,其中课程标准、试卷、教科书,它们的内容都是可以直观呈现的。本文研究的是教师对学生数学认知水平的认知与学生实际数学认知水平的一致性,而学生的数学认知和教师对学生数学认知水平的认知,都是相对内隐的,而且对教师一致性水平的判定需要基于学生认知的“呈现”。
为力求准确地判断学生和教师的相关认知水平,合理地判断二者的一致性,本研究的思路为采用以同样的数学问题为测试题目,学生和教师分别按要求回答问题。要求学生解答问题、写出解题步骤,以较全面地呈现其认知过程与结果;要求教师根据数学问题估计、判断学生解答问题的情况并简述理由,以呈现他们对学生认知水平的认知。在此基础上,做两者的一致性分析。
(三)研究工具
本研究采用的研究工具是课题组①本文中的课题组均指全国教育科学规划课题中小学数学教育研究专项“中学数学教学与学生学习心理一致性的调查研究”(GIA117004)课题组。编制的调查问卷。调查问卷针对不同的知识内容分为学生问卷和教师问卷。为了尽可能全面地反映初中数学教师对学生认知水平的认知和学生认知水平的一致性问题,本研究选取了初中代数、几何和概率中比较有代表性的四部分内容:一元一次方程、函数、等腰三角形和概率,涉及了初中三个年级的数学课程内容。
每份学生问卷由若干具体的数学题目组成,每一道题目都按照课题组根据布卢姆教育目标分类学编写的数学认知水平分析框架中的六个认知水平(记忆、领会、运用、分析、评价、创造)为依据进行设计②L.W.安德森等编著,皮连生主译:《学习、教学与评估的分类学:布卢姆教育目标分类学》(修订版),上海:华东师范大学出版社,2007年版。。为了从多角度考察教师的一致性水平,相应的教师问卷包括了问卷一和问卷二。问卷一是根据学生问卷中题目的几种可能解答情况编制而成,教师根据问题和对自己任教班级学生相关认知水平的把握,填写符合具体解答情况的学生人数或百分比、最易产生的错误等。问卷二将六个认知水平结合具体的数学教学内容进行了陈述,让教师据此填写符合相应认知水平的自己任教班级的学生人数比例。这两个问卷,一个是从具体的题目出发,较为精确地测量教师对学生认知水平的认知程度,即微观测评;一个是从知识的六个认知水平的描述出发,测量教师对学生认知水平的宏观把握程度,即宏观测评。
针对四部分数学知识内容,本研究编制了12份问卷。每一份问卷设计经历了题目征集①提供题目的人员包括教授1名,大学讲师1名,在读博士1名,在读硕士1名,在职中学教师13名。、课题组研讨、题目筛选与改编、专家咨询②本研究共咨询专家8位,其中大学教授2人,大学讲师2人,中学高级教师3人,数学教育博士生1人。-调整、试测-调整等过程,以确保问卷具有较好的信度和结构效度。
(四)被试
本研究采取方便抽样方式选择在北京市两所学校开展调查研究,其中A校为北京市城区的一所完全中学,其高中为北京市示范高中;B校为北京市郊区的一所普通学校。
研究选取两所中学初中年级的16位数学教师及其任教的16个班级共486名学生为被试。16位教师以教龄为主要条件进行选取,其中教龄在十年以上的有10人,十年(含十年)以下的有6人;带任教班时间长于一年的有7人,少于一年的有9人。16个班中,初一年级4个班,初二年级7个班,初三年级5个班③需要说明的是,学校B 为了拉开被试教师的教龄差距,有一节初二等腰三角形课的授课教师是临时调来在这个班上课,她当时是初三某班的数学任课教师。为了了解这位教师对她所带班级学生的了解情况,我们收集的问卷测试数据是她任教初三这个班的数据。所以有一个初三班级做的问卷是初二的知识内容。;其中实验班10个④为叙述方便,本文将直升班、数学实验班、实验班统称为实验班。,普通班6个。
(五)调研实施
研究设计在四部分内容中各选1 课时在每所学校选择两个班进行课堂观察和测试,两个班的任课教师尽可能在教龄、性别方面具有代表性和差异性。但实施中依据学校具体教学进度与安排做了调整,最终调研一元一次方程内容共4个班(A、B校各2个班),函数内容B校2个班,等腰三角形内容共6个班(A校4个班,B校2个班),概率内容共4个班(A、B校各2个班)。下校调研工作在2012-2013年秋季一个学期内完成,主试均为本课题组成员。
三、数据处理
(一)数据编码
被试教师编码由两个字母和一个数字组成,其中第一个英文字母表示该教师所在的学校(A或B);第二个英文字母表示该教师的授课内容,E表示一元一次方程,F表示函数,T 表示等腰三角形,P 表示概率;数字表示该教师的编号,对于前两个字母相同的教师,编号按照教师姓氏的首字母顺序排列。如BT1 表示B校授课内容为等腰三角形,编号为1 的教师。类似地,对被试班级也进行编码。
(二)标准化一致性指数ZH值的计算
1.数据汇总与处理
将每一位被试教师及其学生的原始数据分别统计填入问卷数据汇总表中。以教师BT2 与其所教班级问卷一数据为例,该班学生总数为23人,调研被试的学生人数为23人。将学生问卷和教师问卷一的测量结果数据填写到问卷数据汇总表中,如表1所示。其中,教师问卷数据为教师填写的数据,学生问卷数据为该班符合对应答题要求学生的实际人数。之后将数据转化为百分比的形式并作归一化处理。
2.计算一致性指数P值
在众多的一致性研究中,SEC 方法得到了广泛的应用,其突出的特点是给出了计算一致性指数的公式,使得一致性结果更为精确简明。本研究采取SEC 方法计算被试教师的一致性指标P值:其中xi,yi分别为归一化处理得到的教师问卷和学生问卷数据中的第i个值,xi和yi的取值范围从0 到1;n 为问卷中学生解答的情况数(表1 中n =17)。显然,0≤P≤1.P值为1 表示完全一致,即教师对学生认知的认知和学生实际的认知情况完全吻合,P值为0则表示完全不一致,即教师对学生认知的认知和学生实际的认知情况完全不吻合。按照这样的方法我们得到每位被试教师相对于自己任教班级问卷一和问卷二分别对应的一致性指数P值。
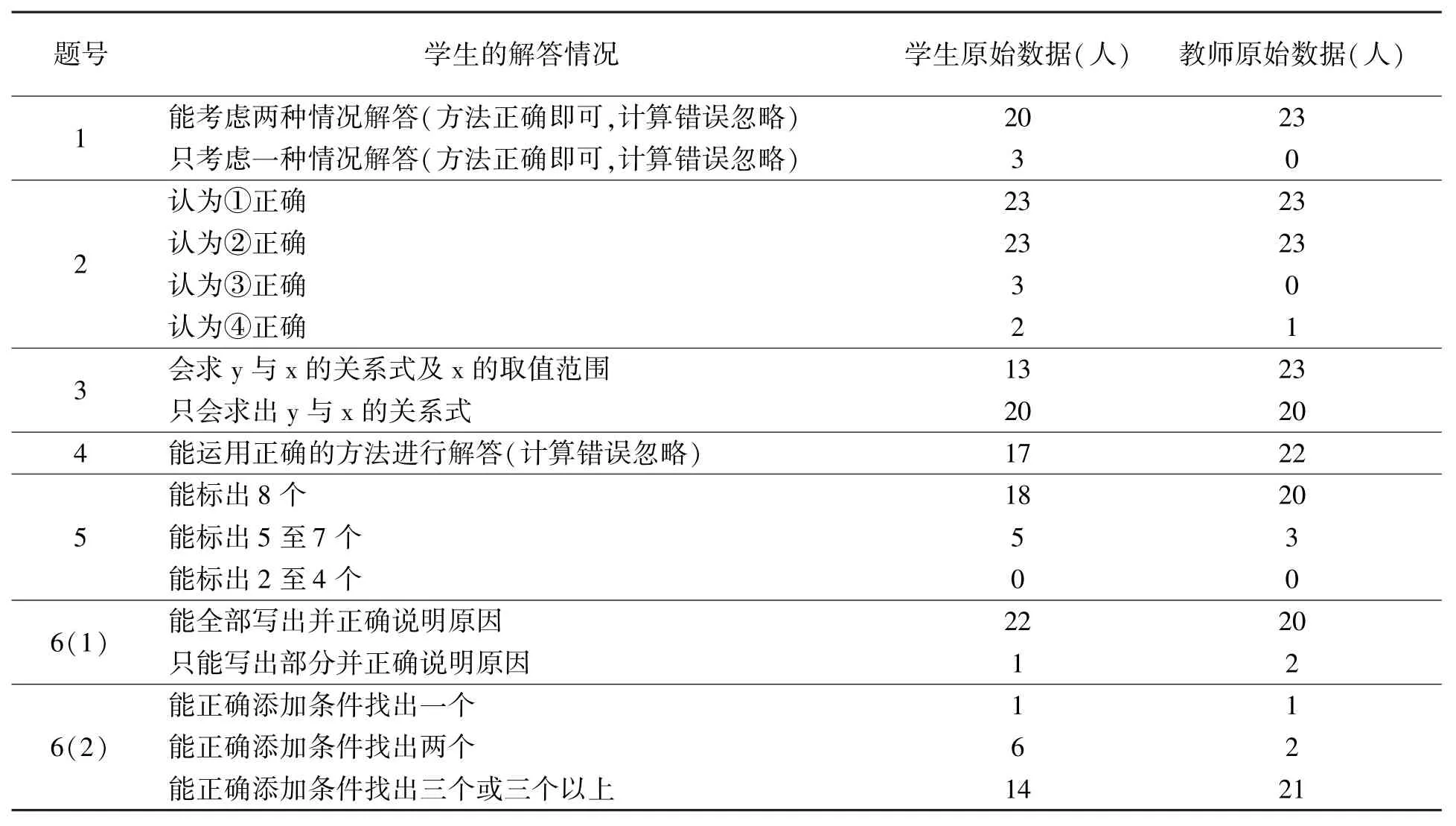
表1 BT2问卷一数据汇总表
3.求每一位被试教师一致性水平的标准值
虽然SEC 方法可用于多方面一致性的研究,但由于其产生的背景与20世纪80年代美国基础教育实践对评价与课程标准一致性分析程序与工具研发的需求直接相关①刘学智、马云鹏:《美国“SEC”一致性分析范式的诠释与启示——基础教育中评价与课程标准一致性的视角》,《比较教育研究》2007年第5期,第64-68页。,研究者多运用SEC 方法研究文本间一致性。文本的参照标准是一样的,比如课程标准相对于试卷来说是固定不变的,所以对于同样的课程标准可以测出试卷与之的一致性水平,而且不同试卷的一致性水平具有可比性。然而,本研究中每位教师对应不同的班级,班级中学生的人数、学习情况都有所不同,针对不同知识点的数学测试题目也不同,这就使得直接用SEC 方法得到的一致性指数P值不仅没有统一的标准,也不具有可比性。至此,我们面临必须解决的两个问题:其一,如何依据P值说明教师一致性水平的高低?换言之,需要确定一个标准值作为衡量的尺度,这个标准值也称为显著性P值。其二,不同教师的P值之间是否具有可比性?亦即需要确定一个可比的标准。
解决第一个问题,本研究借鉴了Liu 等人解决问题的思路②Liu,X.F.,Zhang,B.H.,Liang,L.,Fulmer,G.,Kim,B.,Yuan,H.Q.Alignment Between the Physics Content Standard and the Standardized Test:A Comparison Among the United States New York State,Singapore,and China-Jiangsu.Science Education,2008,93(5):777-797.,显著性P值的算法如下:构造与学生表格中数据生成的一行n 列矩阵A 同样结构的矩阵B。B 中每个元素从0~m 随机生成,m为该班学生总人数。每生成一个矩阵B,就用SEC 方法计算得到一个P值。重复这样的运算20000次,得到20000个P值,事实表明这20000个P值呈正态分布。在0.01 的显著性水平上拟合它的正态分布曲线,求出均值和方差。利用均值和方差可以求得0.05 水平和0.01 水平对应的参考值,以这两个水平的参考值作为判断该教师一致性水平的标准值。整个过程通过MATLAB编程实现。表2 为教师BT2 的数据输出结果,由计算可得教师BT2 的问卷一、问卷二的一致性指数P值分别为0.89 和0.94,0.89 高于0.01 水平参考值0.71,而0.94 高于0.05 水平参考值0.91但低于0.01 水平参考值0.97。显然,每一位被试教师的P值对应不同的分布。
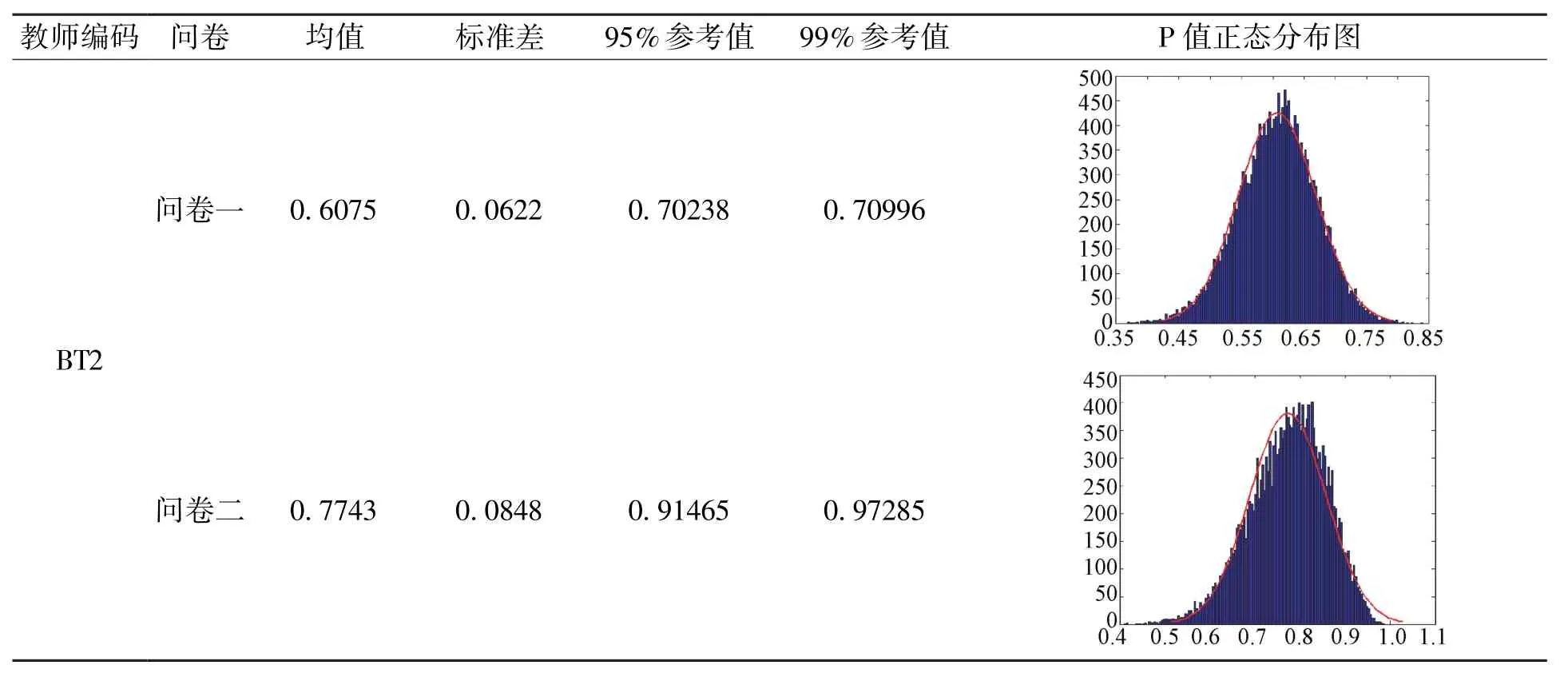
表2 被试教师BT2的P值正态分布图
4.求标准化一致性指数ZH值
为了解决第二个问题,对不同教师之间一致性水平进行比较,我们对P值做标准化处理,即将其转化为标准正态分布上对应的值,记为ZH值。转化公式为其中u和σ为正态分布的均值与方差。经过标准化处理之后,我们得到了所有被试教师的ZH值。这些ZH值都在同一个标准正态分布上,可以直接与标准正态分布0.05 和0.01 显著性水平分别对应的值进行比较,来判断被试教师所达到的一致性水平。计算教师的ZH值是本研究的一个难点和创新点。
四、结论与讨论
(一)初中数学教师的一致性水平总体良好
我们以上述所得标准正态分布均值、0.05 和0.01 显著性水平的对应值0,1.65 和2.33 这三个数作为划分教师一致性水平的标准,称均值以下的水平为高度不一致,均值至1.65(不含)为基本不一致,1.65(含)至2.33(不含)为基本一致,2.33(含)以上为高度一致。据此,被试教师的宏观、微观一致性水平的整体描述如表3所示。
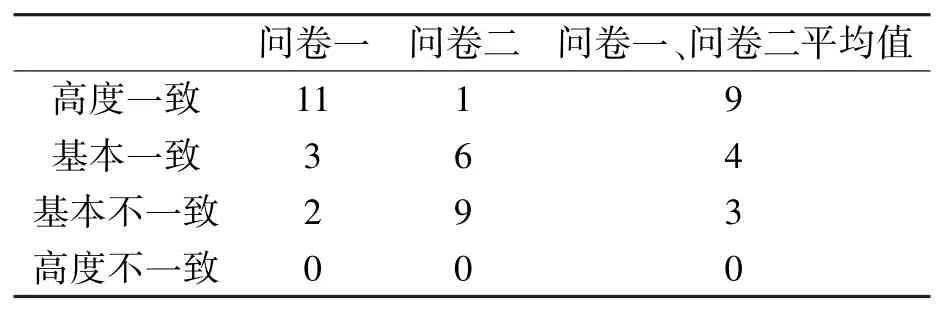
表3 被试教师一致性水平的整体情况
表3显示,两份问卷测得初中数学教师的宏观一致性水平和微观一致性水平都在均值以上。其中,问卷一测得69%的教师达到了高度一致的水平,19%的教师达到了基本一致的水平,只有12%的教师是基本不一致的水平;问卷二测得6%的教师达到高度一致的水平,38%的教师达到基本一致水平,而56%的教师是基本不一致水平。问卷一与问卷二的平均水平显示,56%的教师达到了高度一致的水平,25%的教师达到了基本一致的水平,即81%的教师达到了0.05 显著性水平以上良好的一致性水平,19%的教师处于较低的一致性水平。
本研究在选取调研学校时考虑到了学校的地域、教育质量以及教师的性别、教龄等差异,但统计分析结果表明两所学校的初中数学教师关于学生数学认知的一致性水平并没有显著差异,教师的性别、教龄等因素也未构成教师一致性水平的显著差异。
对于本结论,我们认为数学课程改革突出了对学生数学活动经验的关注,由此也引导数学教师对学生关于数学已经知道了什么、掌握到什么程度,甚至包括如何获得数学知识的关注。调研数据分析以及调研过程中对被试教师所做的访谈都表明,初中数学教师对学生数学认知水平的重视程度在不断提高,对学生数学认知的认知水平也在提高。因而,总体而言呈现出良好的一致性水平。
(二)教师的微观一致性水平要高于宏观一致性水平
对16位教师问卷一和问卷二的ZH值做相关分析如表4所示。

表4 教师微观、宏观一致性水平相关系数矩阵
问卷一和问卷二ZH值的Pearson 相关系数为0.538,p=0.031(p<0.05),故教师的微观一致性水平和宏观一致性水平在0.05 水平上是显著正相关的。数学教师对学生数学认知水平的认知与学生实际数学认知水平的一致性研究本身具有探索性,此研究结果表明,本研究测量一致性水平选取的这两个角度是合理的,无论是宏观还是微观角度,ZH值都可衡量教师对全班学生认知水平的把握程度,只是角度不同教师把握的准确度有所不同。
表3同时说明,被试教师的宏观一致性水平和微观一致性水平之间存在明显差异,教师对学生认知的微观把握水平较宏观把握水平要高,越是细致地针对具体问题分析学生的认知水平,教师越能准确把握。
分析造成教师微观一致性水平与宏观一致性水平差异的原因:一方面,确有相当一部分教师对学生认知水平的了解、把握多拘泥于与解决具体问题的联系,越是细致地针对具体问题的解决分析学生的认知水平,教师表现越好。此说明这部分初中数学教师对学生认识水平的了解还较多停留在具体经验层面,呈现“只见树木不见森林”的特点。我们认为,这是造成本研究结论的主要原因。另一方面,反思本研究,由于测量教师对学生认知水平宏观把握程度的问卷二要求教师从六个认知水平结合具体的数学教学内容进行判断,虽然问卷中对六个认知水平的表现都有描述,但如果教师对六个认知水平理解、把握不准确,也会影响其做出判断。因此,今后的研究中,此环节应与被试教师有充分的交流研讨,使他们对六个认知水平有深入的理解和较好的把握,以避免出现由于对六个认知水平理解不到位而出现判断误差。
(三)教师的微观一致性水平与学生学业成绩呈正相关
我们对问卷一和问卷二的ZH值做了独立样本T 检验分析,其中在班级类型上问卷一ZH值具有显著差异,结果如表5所示。

表5 班级类型的独立样本T检验
表5显示,在微观层面不同类型班级任课教师的一致性水平有显著差异,实验班数学教师的微观一致性水平显著高于普通班的数学教师,但是宏观一致性水平差异不显著。据此可知,学生的学业成绩与教师的微观一致性水平正相关。
教师对学生数学认知水平的认知与学生实际数学认知水平的一致性随着学生数学学业水平的上升而提高,产生这一现象的原因可能来自两个方面:一方面,教师对数学学业水平较高的学生给予了更多的关注,因而可以较准确地把握学生在数学学习细节上的表现;另一方面,数学学业水平较高的学生由于其对数学的理解较好、数学素养较高,因而相对于数学学业水平较低的学生他们在数学学习上表现出较好的稳定性。这一研究结论启示我们,教师不仅需要对所教授学生一般而言的群体性数学认知水平有基本的了解,同时也应对学生个体的数学学习情况有清楚的把握,特别应该关注数学学业水平一般或相对较低的学生在数学学习过程中可能遇到的认知困难及其原因分析,从而帮助学生有效度过数学学习上的每一个难关。
(四)总体而言,教师倾向于高估学生数学认知水平
无论是出于对优秀学生培养的需要,还是出于应试环境的影响,学校一般会分配业务能力较强的教师教授实验班的数学课。因此,得到结论三似乎是在意料之中的事情。但结论四呈现了教师在评估学生数学认知水平倾向性方面的一个有趣现象:同样是微观层面,实验班教师较普通班教师更倾向于低估学生的数学认知水平。这是因为实验班的教师对学生抱有更高的期望值还是其他原因,这是一个值得思考和后续研究的问题。
五、启示
(一)对教师教育的启示
本研究的目的是希望能够进一步唤起教师对学生数学认知的关注,自觉提升和全面把握学生数学认知的能力。本文调查研究的结论反映出被试教师在准确把握学生数学认知水平方面确有不足。教师教育应重视对职前和在职教师“教的意识”的培养,使教师对数学课程、学生数学学习和数学教学能够整体把握。教师既要把握所教授数学知识的内涵实质,又要清楚以数学知识为载体所展开的数学教学活动让学生真正受到的教育是什么。对学生数学认知水平的认知是影响教师高质量地开展数学教学的重要因素,如何使教师超越对学生解决具体问题行为的判断而达到对学生数学认知水平的把握,是教师教育应该努力做到的。
(二)对一致性研究的启示
教育领域中的一致性研究,对教师教学、学生学习、教学评价、教师教育、教育政策的制定等都会产生一定的影响。特别是当一致性研究呈现出具体差距的时候,相关者通过分析思考产生差异的原因,从而对改进教育教学实践、缩小差距产生引导作用。我国教育领域的一致性研究需要突破现有研究思路,在借鉴国外已有研究成果的基础上,进行本土化创新,开拓研究的领域与路径。
虽然本文呈现的仅仅是对教师一致性水平的部分量化分析过程和结果,对于一致性水平具有差异的教师的课堂教学特点、相关影响因素等问题的分析仅通过数据是很难全面反映的,还需要采用课堂观察与访谈等多种方法进行深入的分析与研究。本文对研究内容与方法较为详细的呈现显示,无论是一致性研究的思想、内容还是一致性研究的方法,都有较为广阔的发展空间。
