渐缩-突扩流道水力特性研究

仵峰, 董晓爽, 吴玉博, 马地， 冯雪芳

(1.华北水利水电大学 水利学院,河南 郑州 450045； 2.河南省节水农业重点实验室,河南 郑州 450046)



渐缩-突扩流道水力特性研究

仵峰1,2, 董晓爽1,2, 吴玉博1,2, 马地1,2， 冯雪芳1,2

(1.华北水利水电大学 水利学院,河南 郑州 450045； 2.河南省节水农业重点实验室,河南 郑州 450046)

滴头是滴灌系统的关键部件，流道设计是其核心技术。为了揭示滴头流道内的水流运动规律，提出一种渐缩-突扩的流道结构，以三角形、圆形和流线型作为分水结构形状因素，以流道收缩后最小断面尺寸(边壁距离)和放大比例等作为设计因素，进行了3因素3水平正交试验设计；建立了流道的CFD模型，利用Fluent软件进行数值计算，对不同正交试验处理下的流道内部流场进行了研究。以滴头流量为评价指标，探讨了以上各因素对滴头流量的影响，分析了流道不同断面位置处的能量及其变化规律。结果表明：1)10 m水头条件下,试验各因素均对滴头流量产生影响，其中流道尺寸比例系数对流量的影响最大,流道内分水结构的形状和边壁距离影响不显著，流道的过流能力可用以上参数的多元线性回归方程定量表示；2)渐缩-突扩流道结构的流态指数为0.494 3～0.509 1，属孔口出流；试验的3种因素对流态指数x的影响由大到小依次为：尺寸比例系数、分水结构形状、边壁距离，但均达不到显著水平；3)流道内水流的雷诺数Re的范围为614～691 5，局部水头损失系数为2.1～10.6。

流道结构;尺寸;水力性能;水头损失

灌水器在滴灌系统中属于关键部件,灌水器的流道形式影响着其内部的水流情况和消能效果。Glaad等[1]认为,流道的形式构造、尺寸和材料性能都影响着灌水器的性能；Ozekici等[2]认为,局部水头损失是灌水器消能的主要原因。目前的研究中,一般都是选用一种材料，重点研究结构形式和尺寸大小对灌水器性能的影响。张琴等[3]依据灌水器内的流线,将矩形迷宫流道结构优化成圆弧形,使它的水力性能得到了提高。孟桂祥等[4]利用流线型流道对传统的迷宫流道进行结构优化,改变其中的水流流态,提高了灌水器的消能效果。李云开等[5]设计了新型的分型流道结构灌水器,分型流道水流大部分呈紊流状态,消能效果较好。郭霖等[15]采用均匀设计的试验方法,对三角形的迷宫流道进行模拟,得到了各个参数对其水力性能的影响关系。刘春景等[6-7]利用响应曲面法对三角形和梯形流道进行了研究,得到了流道内各结构参数对流量和流态指数的影响关系。喻黎明[8]研究了正交试验下的16种梯形流道的各结构参数对其水力性能的影响关系。王建东等[9]通过回归分析得到了滴头流量与各参数之间的函数关系,研究了不同流道结构参数对灌水器水力性能的影响。

计算流体力学(Computational Fluid Dynamics，CFD)的发展为灌水器内水流流动特性研究提供了一种新途径,采用CFD进行模拟，耗时短、成本低,在一定程度上弥补了理论分析和试验测试的不足。王尚锦等[10]、李永欣等[11]、颜廷熠等[12]均基于CFD流场模拟方法，对滴头内部流场的压力-流量关系和内部的水流特性进行了模拟和室内试验验证。田济扬、郭霖等[13-15]研究了一种八字形和“V”字形相结合的新型滴灌双向流道结构,利用Fluent模拟结果表明,流道是通过正、反向水流混掺达到消能效果的。

优化流道结构是滴头设计中常用的方法，如迷宫式滴头就是采用优化后的齿形流道。苑伟静等[16]设计了一种利用渐扩、渐缩、分流的新型流道形式。这类灌水器流道形状对灌水器的水力性能影响显著。水流在流道内流动时,由于流道结构的突变(突扩、突缩),导致流速分布改变，流层间切应力增加,水流强烈紊动,将产生较大的能量损失,因而其消能以局部水头损失为主。

本文以渐缩-突扩结构的流道作为研究对象，考虑其最小断面尺寸和结构总体尺寸等因素，利用CFD技术研究流道的过流特性和消能效果,以期为新型滴灌灌水器的流道设计提供理论支持。

1 新型流道结构的构建

出流稳定是对灌水器性能的基本要求之一,良好的消能结构是达到这一目标的重要途径。参考迷宫滴头的流道结构，提出一种渐缩-突扩结构作为流道的基本结构,利用局部突变影响水流的流态,从而增加局部水头损失。为使流道内水流充分混掺,增加流道的消能效果,提高出流的稳定性,需要考虑最小断面处的尺寸(以下简称为边壁距离)和流道平面上的放大因子。以三角形、圆形和流线型作为收缩段形状因素，结合流道收缩后边壁距离和不同放大比例等作为流道设计因素，对流道结构进行设计。

1.1 流道结构形式

当有压水流进入流道后,通过内部的流道分水结构达到分流的目的,该分水结构选用简单的三角形、圆形以及符合水流流线的流线型3种形式作为流道的形状因子,滴头流道结构如图1所示。

图1中，左侧为进水口,在进水口后设置有导流板,以提高水流到达结构体前的均匀度,右侧中部的圆形为水流出口；沿流道设置4个断面，用来考查水流在断面处的流速和能量分布。

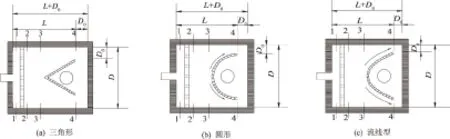
图1 滴头流道结构形式

1.2 流道结构参数

流道结构与其相关参数是影响灌水器水力性能的重要因素。根据图1,选取形状、边壁距离D0、尺寸比例系数(以下简称尺寸比)作为关键因素,其中尺寸包括流道长度L、流道宽度D、流道深度,原型流道深度取为0.5 mm,L为6 mm,D为3 mm,各因子水平见表1。

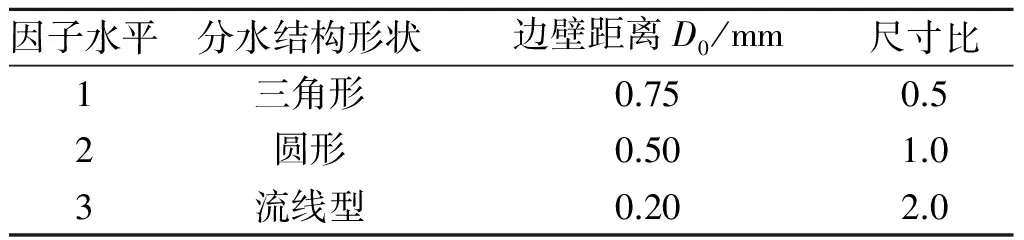
表1 各因子水平的选取

按照表1的因素水平，暂不考虑各因素间的交互作用,采用正交试验方法,设计了3因素3水平的正交试验，进行了9次模拟试验研究。

1.3 网格划分及边界条件

利用Pro/E软件绘制出流道结构的3D模型。由于流道结构形式比较复杂,因此网格类型采用混合的多面体网格,网格尺寸设置为0.1,利用Gambit软件对网格进行划分,然后将生成的.msh文件导出,再利用Fluent软件进行计算。流道进口的边界条件设为压力边界(pressure-inlet),压力分别设置为2、3、5、6、7、8、9、10、12、14、15 m水头；出口也为压力边界,设定为标准大气压,即压力水头为零。

数值计算时,选取定常的非耦合隐式算法,对流项等采用二阶迎风格式,速度耦合用SIMPLE算法,残差标准设为10-4。

由于该流道结构的复杂性,因此选择湍流模型来进行模拟。针对不同的湍流需要应用不同的湍流模型,其中标准k-ε模型应用广泛,k为湍流动能、ε为动能耗散率,该模型具有很好的收敛速率和相对较低的内存要求。k-ω模型与k-ε模型类似,其中ω为大涡频率,可以很好地描述近壁面内的边界层流动。另外,剪切应力湍流模型(SST模型)保留了k-ω模型的近壁面的特性,但是SST模型并非总能快速收敛得到解。综上,针对流道的结构特点,参考以往研究滴头流道的CFD模拟结果[4,11-12,14],选用标准k-ε模型进行计算。

2 结果与分析

在一定的压力范围内,流道的过流能力即为滴头流量,用压力-流量关系表示为:

q=khx。

(1)

式中:q为滴头流量,L/h;h为压力水头,m;k为流量系数(与几何尺寸有关);x为流态指数。

利用Fluent的流量统计功能，得到各试验组合在不同压力下的流量值,见表2。用式(1)拟合得到各试验组合的压力-流量关系,其对应的流态指数x和流量系数k也列于表2。

由表2可知,随着压力的增大,流道的过流能力增大。结合试验因素及水平可以得出,同一结构形式、同一压力条件下,结构的尺寸比越大,对应的流量q越大;边壁距离越大,流量q也越大。但流道内水流的流态指数x变化不大,其取值范围为0.494 3～0.509 1,接近孔口出流(x=0.5)时的流态。

表2 不同水头压力下的流量q值

2.1 流道结构参数对滴头流量的影响

2.1.1 直观分析

10 m水头下流道结构参数对滴头流量影响的直观分析结果见表3。

表3 正交试验直观分析结果(h=10 m)

由表3可知,当边壁距离和尺寸比水平变动时,流道过流能力波动较大;当分水结构形状变动时,流道的过流能力变化较小。表明研究的渐缩-突扩流道结构的过流能力,与流道的分水结构形状、边壁距离和尺寸比均有关。尺寸比对滴头流量的影响最大,即流道的尺寸成倍缩小或放大时,其相应的过流能力也将急剧缩小或变大;而试验条件下的边壁距离和分水结构形状对流道的过流能力影响不大。

2.1.2 方差分析

直观分析法虽然简洁直观,但它不能辨别造成试验结果波动的原因,如因素水平的改变可以引起试验结果的波动,而试验误差也有可能引起试验结果的波动;同时也没有提供一个标准来判断因素的作用是否显著。为了克服这些不足,需结合方差分析进行研判,方差分析结果见表4。

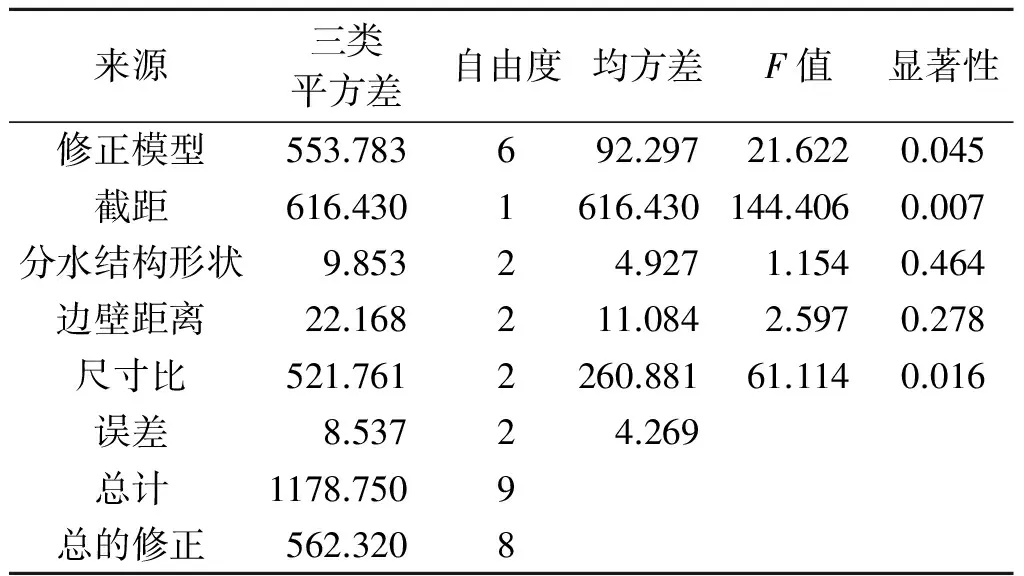
表4 流道结构参数对流量影响的方差分析

由表4可以看出，按照α=0.05来检验时,尺寸比对滴头流量的影响比较显著,说明结构参数中尺寸比对流量的影响最大,流道内的形状与边壁距离对流量的影响效果不显著。各结构参数对流量q的影响顺序由大到小依次为:尺寸比、边壁距离、分水结构形状,这与极差分析结果相吻合。

2.2 流道结构参数对滴头流态指数的影响

流态指数x与流道的结构参数紧密相关,反映了灌水器流量对压力变化的敏感程度,可以用来评价流道水力性能的优劣。其值越小,对应滴头的水力性能越好。

首先采用直观分析法进行初步分析。结果表明,流道结构参数对流态指数x的影响顺序由大到小依次为:尺寸比、分水结构形状、边壁距离。

按照α=0.05来进行正交检验,方差分析结果见表5。

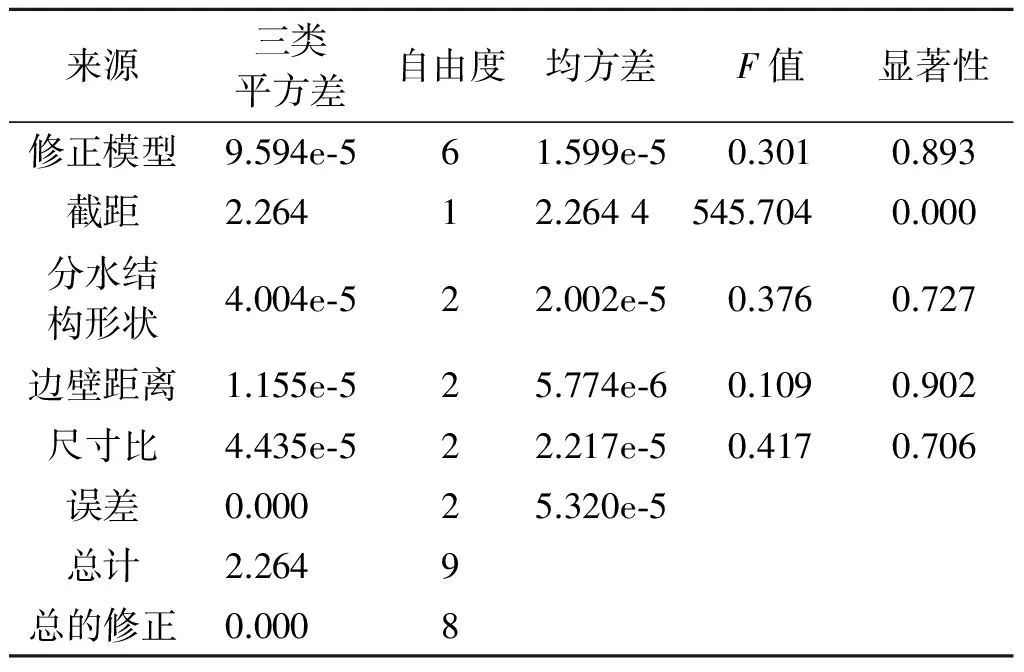
表5 流道结构参数对流态指数影响的方差分析

从表5可以看出,3种因素对流态指数x的影响

均不显著,各结构参数对流态指数x的影响顺序由大到小依次为:尺寸比、分水结构形状、边壁距离,结果与极差分析结果吻合。

分析各参数对流态指数x的影响,由表5可以看出各种组合条件下流态指数变化不大，表明流动状态相同。这一结果同时也说明,采用标准k-ε模型来进行模拟计算是恰当的。

2.3 滴头流量与流道结构参数的线性回归分析

由以上分析可知,流道结构参数影响滴头流量。因此,以正交试验得到的结果为依据,采用SPSS进行多元线性回归分析,得到10 m水头下滴头流量与流道各结构参数的多元线性回归方程:

q=-14.899+1.218A+6.388B+8.826C。

(2)

式中:A为分水结构形状，三角形、圆形、流线型对应取值分别为1、2、3;B为边壁距离,mm;C为尺寸比。

线性回归的相关系数R=0.938。F检验在α=0.05时,达到显著水平。对各回归系数进行t检验(见表6)，在α=0.05时，尺寸比达到显著水平。

表6 回归系数的t检验

2.4 流道内水流流态以及消能效果

利用CFD模拟的后处理功能,可以直观地得到不同试验条件下的速度场和压力场,如图2、图3所示。

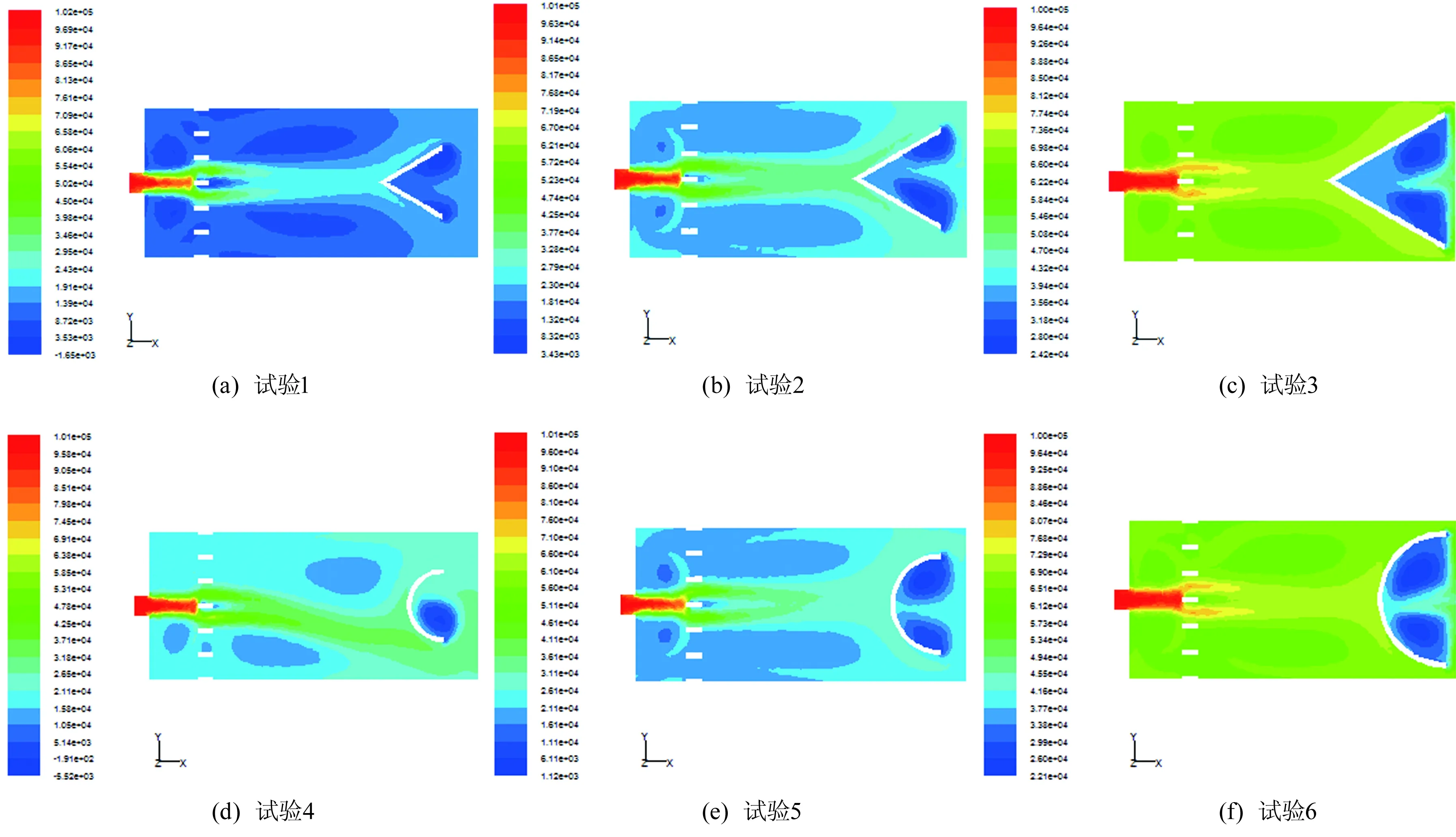
图2 不同试验条件下的压力分布

图3 不同试验条件下的流速分布

从图2、图3中压力场和流速场的分布可以看出：通过导流板稳流后,水流到达渐缩段前,压力场分布比较均匀;流速场存在一定的主流区,但涡旋现象并不明显,而在水流到达突扩断面(断面4—4)后,由于出水口设置在挡水结构体内,出现了明显的回流和涡旋。

为了分析渐缩-突扩结构的消能效果,需要计算各断面的能量。计算时,把各断面平均分成30份,先利用软件的自带功能,根据观测点统计出每一断面不同位置处的流速和压强,再分别计算出该断面的动能和压能，最后用式(3)计算出各个断面的总能量。

(3)

式中:z为位置水头,m;p为压强,Pa;u为流速,m/s;ρ为水的密度,kg/m3;g为重力加速度。

计算时,对断面4—4按照水流运动方向分成2部分(即两边收缩断面最窄处与回流区),分别进行统计分析,结果见表7。分析表7可以得出,从断面3—3到断面4—4两端最窄处为渐缩段，而断面4—4两端最窄处到断面4—4的回流区为突扩段,以断面3—3为基准,渐缩段消耗能量为43.68%～58.70%,与之对应的突扩段消耗能量为9.30%～26.69%。因此,采用渐缩-突扩结构的流道能量消耗以渐缩段为主，这与常规的水头损失不同。产生此种现象的主要原因是该结构中突扩后的距离仅为1倍的最小断面尺寸,水流经过渐缩-突扩结构后并没完全稳定,因而突扩后的消能效果并没完全发挥;此外,在突扩段能量分析时,试验1、4、7回流区压力出现负值,而试验3、6、9的能量出现了增加现象,水流不稳定是造成上述结果的重要原因。

水头损失hw由沿程水头损失hf和局部水头损失hj组成。经计算,不同试验处理下的水头损失及雷诺数结果见表8。由表8可以看出,在10 m水头时：①流道内的雷诺数Re的范围为614～691 5;②内部结构相同,随着边壁距离的减小,局部水头损失系数变小,在边壁距离为0.75 mm时,局部水头损

失系数最大;③尺寸比相同,随着边壁距离减小,局部水头损失系数变大;④边壁距离相同,尺寸比对局部水头损失系数的影响不明显。

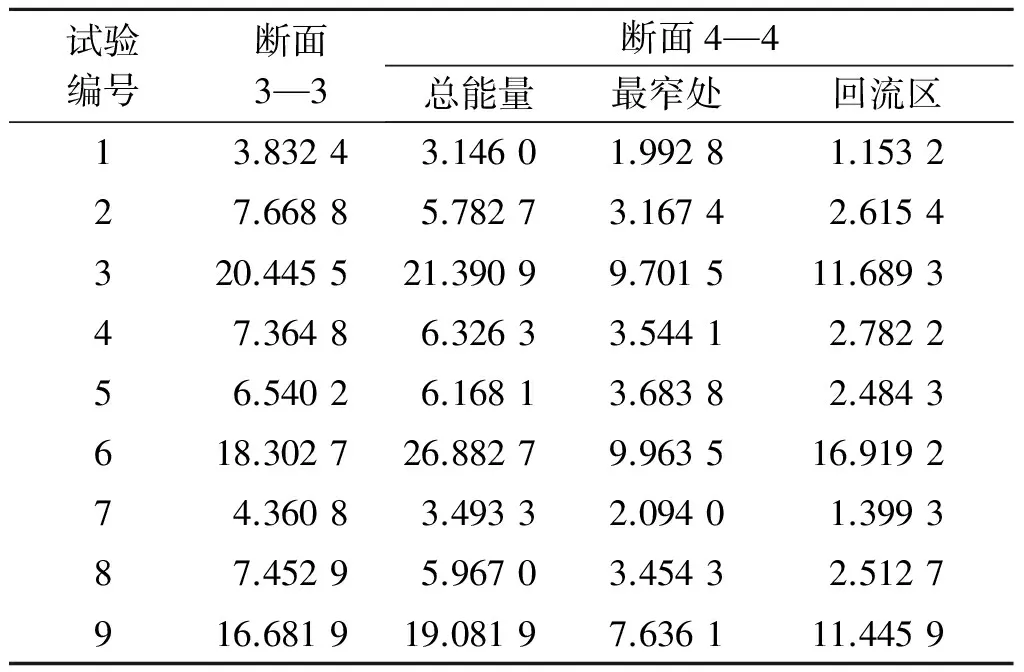
表7 各断面总能量

表8 流道结构内的水头损失及雷诺数(h=10 m)

3 结语

通过对新建的突变结构流道进行Fluent模拟,可以得到如下结论:

1)各结构参数均对滴头流量产生影响。在10 m水头下,流道尺寸比例系数对流量的影响最大，流道内分水结构的形状和边壁距离影响不显著。

2)各结构参数对滴头流态指数x的影响均不显著,标准k-ε模型适宜于模拟渐缩-突扩流道结构内的水流运动。

3)在10 m水头下,滴头流量可用结构参数的多元线性回归方程表示。流道内的雷诺数Re为614～691 5,流态指数为0.494 3～0.509 1,属孔口出流,局部水头损失系数为2.1～10.6。

为提高流道的消能效果,可以在流道结构中增加多个渐缩-突扩结构,以增大局部水头损失,使水流充分混掺,达到消能的目的。每个结构之间的间距需要进一步研究确定,在提高滴头水力性能的同时,还应该考虑流道的抗堵性能。

[1]GLAAD Y K,KLOUS L Z.Hydraulic and mechanical properties of drippers[C]//Proceedings of the 2ndInternational Drip Irrigation Congress，1980:7-14.

[2]OZEKICI B,RONALD S.Analysis of pressure losses in tortuous path emitters[J].American Society of Agriculture Engineering,1991，34:112-115.

[3]张琴,叶含春,管瑶.矩形迷宫式滴灌灌水器结构参数及水力特性研究[J].农机化研究,2012,34(1):190-194.

[4]孟桂祥,张鸣远,赵万华，等.滴灌滴头内流场的数值模拟及流道优化设计[J].西安交通大学学报,2004,38(9):920-924.

[5]李云开,杨培岭,任树梅,等.分形流道设计及几何参数对滴头水力性能的影响[J].机械工程学报,2007,43(7):99-114.

[6]刘春景,唐敦兵,何华,等.滴灌三角形迷宫滴头水力性能稳健性分析[J].农业机械学报,2013,44(1):68-72.

[7]刘春景,唐敦兵,郑加强,等.滴灌梯形迷宫滴头流道水力性能的响应曲面法优化[J].农业工程学报,2011,27(2):46-51.

[8]喻黎明.结构参数对梯形流道水力性能及抗堵塞性能的影响[J].西北农林科技大学学报(自然科学版),2011,39(8):197-202.

[9]王建东,李光永,邱象玉,等.流道结构形式对滴头水力性能影响的试验研究[J].农业工程学报,2005,21(增刊1): 100-103.

[10]王尚锦,刘小明,席光,等.农灌用新型迷宫式滴头内流动特性分析[J].农业工程学报,2000,16(4):61-63.

[11]李永欣,李光永,邱象玉,等.迷宫滴头水力特性的计算流体动力学模拟[J].农业工程学报,2005,21(3):12-16.

[12]颜廷熠.基于CFD模拟的迷宫滴头工作性能研究[D].北京:中国农业科学院研究生院,2008.

[13]田济扬,白丹,任长江,等.滴灌双向流流道灌水器水力特性分析[J].农业工程学报,2013,29(20):89-94.

[14]田济扬,白丹,于福亮,等.基于Fluent软件的滴灌双向流流道灌水器水力性能数值模拟[J].农业工程学报,2014,30(20):65-71.

[15]郭霖,白丹,程鹏,等.三角形迷宫流道滴灌灌水器结构参数及水力特性研究[J].中国水能及电气化,2011(10):23-27.

[16]苑伟静,魏正英,楚华丽,等.分流式灌水器结构优化设计与试验[J].农业工程学报,2014,30(17):117-124.

(责任编辑：宰松梅)

Hydraulic Properties of the Flow in a Gradual Shrinking and Sudden Enlarging Channel

WU Feng1,2, DONG Xiaoshuang1,2, WU Yubo1,2, MA Di1,2, FENG Xuefang1,2

(1.North China University of Water Resources and Electric Power, Zhengzhou 450045, China; 2.Henan Key Laboratory of Water-saving Agriculture, Zhengzhou 450046, China)

Emitters are important parts in a drip irrigation system. The flow channel design is the key technology for emitters. To reveal the hydraulic properties of water in its path, a new structure of the gradual shrinking and sudden enlarging channel was put forward. An orthogonal experiment under three factors and three levels was built. Three experimental factors are the shape of diversion structure, which include triangle, circle and streamline, the size of the narrowest section and the scale ratio. A CFD model was established and FLUENT was adopted to carry on the numerical simulating water flow field in the structure. The internal flow field was studied under different orthogonal tests. Influences of all above factors on the discharge, the energy and its head loss were analyzed in the different cross-section along the channel. Results show that: 1) all factors in the experiment impact on the discharge under 10 m inlet pressure. The influence of the proportional coefficient of channel size on the flow is significant, while the others′ effects are non-significant. Flow capacity can be quantitatively formulated by a multiple linear regression equation of the above parameters. 2) The flow index of gradual shrinking and sudden enlarging channel is 0.494～0.509. Water flow regime belongs to an orifice outflow in such a gradual shrinking and sudden enlarging channel. The effect order of the three factors on the flow indexxfrom the largest to the smallest is as follows: proportional coefficient of size, shape, the narrowest section. But none of them has reached to the significant level. 3) The Reynolds number of the flow across the channel is 614～6 915. The coefficient of local head loss is 2.1～10.6.

channel structure; size; hydraulic properties; the head loss

2017-01-20

国家科技支撑计划课题(2015BAD24B02)；河南省科技攻关计划项目(152102110094)；华北水利水电大学高层次人才科研启动费资助项目(201336)。

仵峰(1969—),男,河南南阳人,教授,博导,博士,从事节水灌溉理论与技术研究及设备研发。E-mail:wufeng@ncwu.edu.cn。

10.3969/j.issn.1002-5634.2017.02.012

TV132+.11;S275.6

A

1002-5634(2017)02-0061-07