计及自由液面影响的水下有限深度圆柱壳自由振动分析
2017-05-17郭文杰李天匀缪宇跃杨国栋
郭文杰, 李天匀,3, 朱 翔, 缪宇跃, 杨国栋
(1. 华中科技大学 船舶与海洋工程学院,武汉 430074;2. 船舶与海洋水动力湖北省重点实验室,武汉 430074;3. 高新船舶与深海开发装备协同创新中心,上海 200240)
计及自由液面影响的水下有限深度圆柱壳自由振动分析
郭文杰1,2, 李天匀1,2,3, 朱 翔1,2, 缪宇跃1,2, 杨国栋1,2
(1. 华中科技大学 船舶与海洋工程学院,武汉 430074;2. 船舶与海洋水动力湖北省重点实验室,武汉 430074;3. 高新船舶与深海开发装备协同创新中心,上海 200240)
提出了一种求解有限浸没深度下圆柱壳振动特性的解析方法。采用镜像原理和Graf加法定理得到流体速度势的解析表达式,然后再结合能量泛函变分方法推导出计及自由液面影响的壳-液耦合振动方程,通过求解该方程,得到结构各阶固有频率。研究表明,相比于无限域,自由液面的存在会增大同阶次模态固有频率,而且离自由液面越近,固有频率越大,但是随着浸没深度逐渐增加,自由振动特性很快趋近于无限域。与有限元软件Nastran计算结果对比表明该方法准确、可靠、简便,且具有计算量小、易于参数优化的优点,也为近水面结构流固耦合振动特性分析提供了新的思路。
自由液面;能量泛函变分;镜像原理;Graf加法定理
圆柱壳-流场耦合振动的研究工作很多, 徐慕冰[1]基于波传播法研究了流场中圆柱壳频散特性及振动能量流机理, Zhang等[2-3]采用同样的方法分析了圆柱壳-流场耦合自由振动特性。曹雷等[4]运用Riccati传递矩阵法和齐次扩容精细积分法求解了水下环肋圆柱壳声振问题,李学斌[5]采用能量法分析了流场中计及静压影响环肋圆柱壳的自由振动问题。但是上述工作中并未考虑自由液面的影响。
自由液面对壳-液耦合振动影响的研究工作较少,Ergin等[6]基于实验和三维水弹性软件对有限浸没深度下圆柱壳振动特性进行分析,发现结构离自由液面越近,同阶次固有频率越大。Amabili[7]对部分充液圆柱壳进行研究,提出了用扇形边界替代自由液面的近似方法。之后, Amabili[8]将该方法拓展到处理部分浸没问题。随后 Ergin等[9]利用边界积分法和镜像原理对部分充液(浸没)圆柱壳振动特性进行研究,结果与实验数据符合良好。王斌等[10]从圆柱壳表面的均方振速和辐射声功率的角度,对半浸状态和全浸状态下圆柱壳在无限长线激励作用下的声振特性进行了比较分析,指出了二者之间的差别与联系。白振国等[11]采用镜像法建立了有限水深环境中二维圆柱壳的振动声辐射数学物理模型,初步计算了浅水对圆柱壳振动声辐射的影响规律及水深、潜深对声场分布和衰减特性的影响规律。Li等[12]基于镜像原理进行了自由液面下有限潜深无限长圆柱壳结构的声辐射性能研究,基于稳相法,最终得到了有限浸没深度下圆柱壳结构远场辐射声压的计算表达式。刘佩等[13]采用有限元软件ANSYS对有限深度浸没圆柱壳进行仿真,得到了和文献[6]类似的结论,并指出自由液面对圆柱壳自由振动的影响在浸没深度大于四倍半径时可以忽略不计。
目前有限元-边界元耦合计算方法是结构-流场耦合分析中比较常用的数值方法,该方法也随之应用到处理自由液面问题[14-16],通过和镜像原理的结合,即对三维声学Helmholtz方程基本解的修正,实现计及自由液面影响的流固耦合振动性能计算。
针对有限元-边界元耦合计算方法建模工作量大、计算时间长的不足,本文提出了一种解析求解近自由液面圆柱壳振动特性的方法。基于势流理论,通过引入镜像原理来处理自由液面处的声学边界条件,利用Graf加法定理[17]对实源和虚源两种坐标系进行转换得到速度势在流场的分布,然后再结合能量泛函变分方法得到壳-液耦合振动方程,进而可以求解其自由振动特性。
1 理论分析
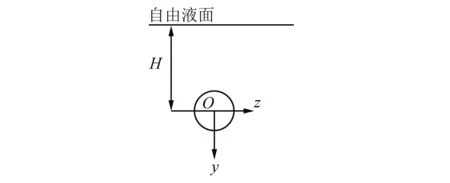
圆柱壳长度为L,厚度为h,中面半径为R,浸没深度为H,u,v,w分别表示轴向、周向和径向的中面位移,壳体材料的密度为ρ,弹性模量为E,泊松比为μ。流体密度为ρf。取圆柱壳左端面中心为坐标原点O,对应直角坐标(x,y,z)。实际分析中选择柱坐标系(x,r,φ),其中,x表示轴向,r表示径向,φ为周向角(与y轴夹角),如图1所示。
为了研究方便,本文取两端简支边界条件,因此位移场如下所示
(1)
(a)

(b)图1 模型及坐标系Fig.1 Model and coordinate system
式中:m为轴向半波数;n为周向波数;Umn,Vmn,Wmm为三向位移幅值;km=mπ/L。
本文采用能量泛函变分的方法研究有限浸没深度圆柱壳振动特性,故首先应得到各部分能量的表达式。
壳体应变能(基于Love壳体理论)可以表示为
(2)
式中:ε为应变向量;σ为应力向量;V表示圆柱壳体积分域。
根据位移函数正交性,积分后式(2)可以写成
(3)
式中:{ξmn}={Umn,Vmn,Wmn}; 刚度矩阵[Kmn]为三阶Hermite矩阵。
壳体动能如下所示:
(4)
同理根据位移函数正交性,积分后可以表示为
(5)
式中,质量矩阵[Mmn]为三阶对角矩阵。
为求解流体做功,首先需要得到速度势函数的解析表达式。
本文基于势流理论,流体视为不可压缩、无旋、无粘性的理想流体,因此速度势函数φ(r,x,φ,t)满足柱坐标系下Laplace方程
(6)
对于水下圆柱壳,满足无穷远处速度势为零的条件
(7)
由于自由液面的存在,可以借鉴镜像原理进行分析,认为速度势可由结构振动直接引起的实源速度势和自由液面反射的虚源速度势叠加组成。虚源坐标系(x′,r′,φ′)与实源坐标系关于自由液面对称,如图2所示。
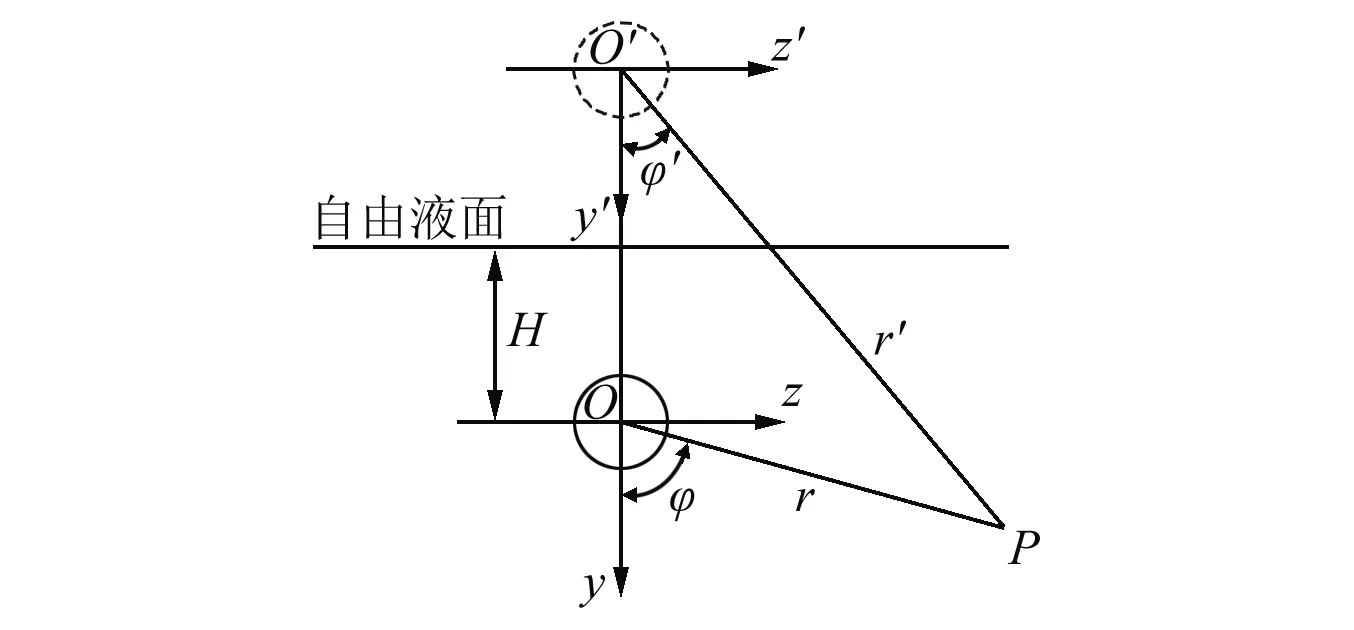
图2 镜像原理示意图Fig.2 Schematic diagram of image method
设流域中任意一点为点P,其速度势函数可以表示为
φ(r,x,φ,t)=φr(r,x,φ,t)+φi(r′,x′,φ′,t)
(8)
式中:φr(x,r,θ,t)表示实源流体速度势;φi(x′,r′,φ′,t)表示虚源流体速度势。
满足式(6)和(7)的速度势函数有以下形式
(9)
式中,Kn()为第二类修正贝赛尔函数。
自由液面处速度势为零
φr(r,x,φ,t)+φi(r′,x′,φ′,t)=0
(10)
当P点位于自由液面上时满足如下位置关系
r=r′,x=x′,φ+φ′=π
(11)
将式(9)、(11)代入式(10),正交化处理后得到
(12)
即可以得到速度势函数的解析表达式:
(13)
根据Graf加法定理
K-n(kmr′)exp(-inφ′)=
(14)
对于有限深度浸没,结构表面处半径r≈R< 2H,因此速度势解析表达式
(15)
因为系数a和n地位等价,交换顺序级数求和后上式改写为
(16)
根据圆柱壳外壁面处速度连续条件,有:
(17)
将式(16)代入式(17)中,正交化处理后可以得到速度势幅值向量{φn}和位移幅值向量{ζn}的关系
{φn}=[Q]{ζn}
(18)
式中,[Q]为迁移矩阵, {φn}={φm,-N,φm,-N+1,…,φm,N}T,{ζn}={Wm,-N,Wm,-N+1,…,Wm,N}T,即可将速度势幅值向量用位移幅值向量表示。
由伯努利方程可以得到壁面处流体动压力
(19)
流体做功为
(20)
由上述各能量分量可得到能量泛函表达式
Π=U-Wf-T
(21)
根据变分原理,满足:
(22)
由对幅值Umn,Vmn的偏导为0,可以得到其与幅值Wmn的线性关系,简写为如下所示的形式
(23)
式中,a1,b1,c1和a2,b2,c2都是关于角频率ω,刚度矩阵[Kmn]和质量矩阵[Mmn]的系数,即Umn,Vmn可由Wmn进行代换。

[Tm]{ζn}=0
(24)
式中,[Tm]为2N+1阶矩阵,元素中含角频率ω。
因为{ζn}中元素不全为0,所以[Tm]必然不是满秩矩阵,即:
det([Tm])=0
(25)
根据上式可以求解出轴向波数m取任意值时各阶角频率ω,从而可以得到固有频率值。
2 数值计算
模型参数:壳长L=1.284 m,半径R=0.18 m,厚度h=0.003 m,壳体密度ρ=7 850 kg/m3,杨氏模量E=206 GPa,泊松比μ=0.3,流体密度ρf=1 025 kg/m3。为了说明方法收敛性,本文取H=0.2 m,计算前十阶频率随截断数N的变化规律,如表1所示。
表1H=0.2 m前十阶频率收敛性分析
Tab.1 Convergence analysis for the first ten natural frequencies whenH=0.2 m Hz

从表1可以看出,截断数N大于等于10以后,各阶固有频率值已经收敛,故后续算例截断数N都取10。本文对于不同浸没深度下前十阶固有频率做过收敛性分析,结果均表明截断数N取10时频率已收敛,限于篇幅,并不赘述。
为验证解析方法的准确性,本文对比了不同浸没深度下解析方法和有限元软件Nastran仿真计算的前十阶固有频率值,如表2所示。
表2 不同深度下解析方法与仿真方法固有频率对比
Tab.2 Comparison of frequencies between analytical method and simulation method in different submerged depth Hz

从表2可以看出,不同浸没深度下解析方法和有限元仿真计算的前十阶固有频率符合的很好,最大误差不超过2%,说明本文方法是准确可靠的。而且随着浸没深度的增加,同阶次固有频率逐渐降低,并且很快趋于无限域的固有频率解析计算值。
为了更直观的了解自由液面对自由振动的影响,本文提取了H=0.2 m以及无限域时解析方法和仿真计算得到的前四阶模态的周向振型及固有频率,如图3所示。
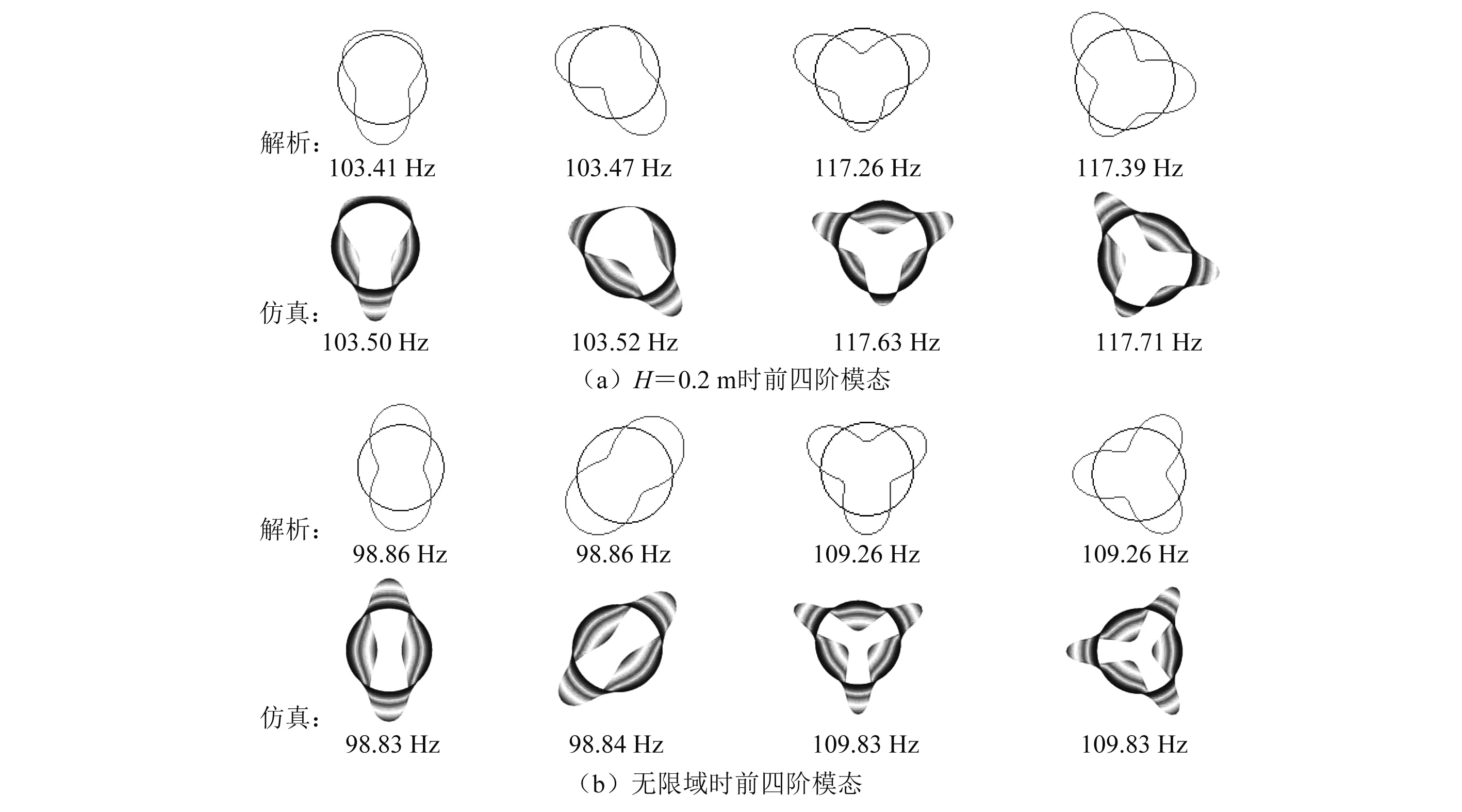
图3 前四阶模态周向振型及固有频率Fig.3 Circumferential vibration types and natural frequencies of the first four order modes
从图3可以看出,受自由液面影响,当浸没深度较小时,模态振型与无限域情况有明显区别,一方面不再是规则的周向波型,令一方面,正反模态频率出现差异。这是由于自由液面的存在使原本正交的周向波出现相互耦合,形成更为复杂的振型。本文方法计算的振型和有限元软件Nastran计算的振型吻合良好,进一步验证了方法准确性。
上述工作研究了自由液面对振动性能的影响,为进一步得到固有频率随浸没深度的具体变化规律,本文绘制了前四阶固有频率随无量纲浸没深度(浸没深度与结构半径比值H/R)的变化曲线,如图4所示。
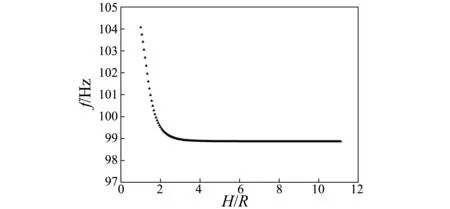
(a) 第一阶固有频率
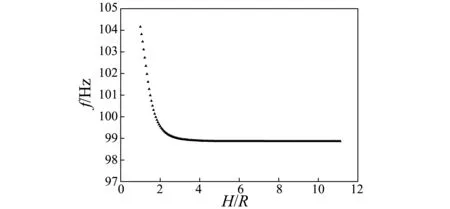
(b) 第二阶固有频率
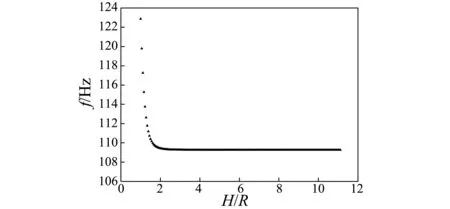
(c) 第三阶固有频率
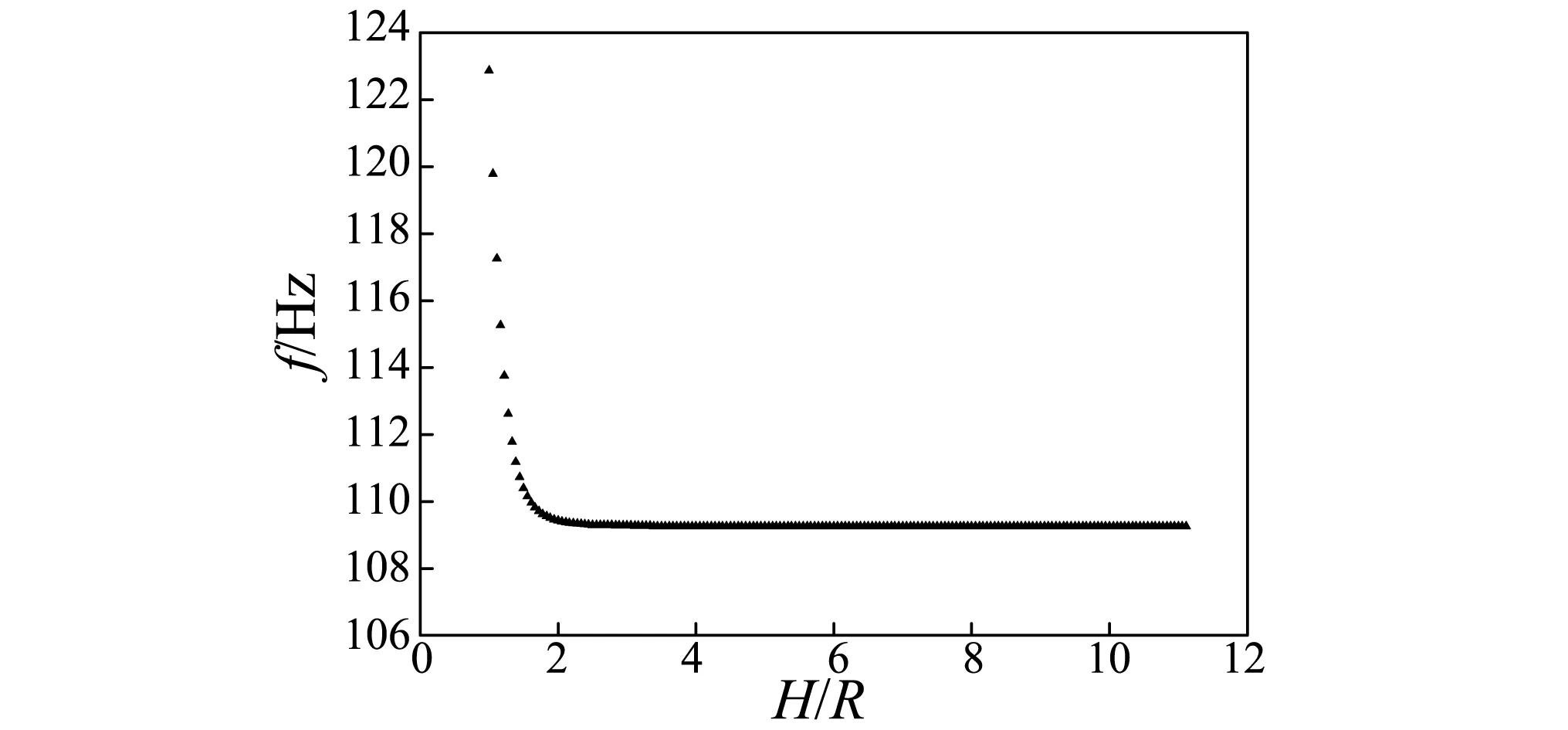
(d) 第四阶固有频率图4 前四阶固有频率随浸没深度变化曲线Fig.4 Curves of the first four natural frequencies in different depth
从图4可以看出,前四阶固有频率值在无量纲浸没深度H/R小于2时变化比较明显,此后随着H/R增大很快趋于平缓,说明自由液面和结构距离在二倍半径以内时才会对结构振动有较为明显的影响。
为确定圆柱壳振动性能趋于无限域时无量纲浸没深度H/R具体取值,定义参数κ=(f-f无限域)/f无限域,其中f为任意浸没深度固有频率,f无限域为无限域同阶次固有频率,κ表征任意浸没深度下固有频率相对于无限域同阶次固有频率的相对偏差。本文取前十阶固有频率,分析无量纲浸没深度H/R分别取1.05, 2, 3, 4, 5时各阶固有频率对应的相对偏差κ的大小(固有频率均是解析方法计算得到且保留小数点后两位),如表3所示。
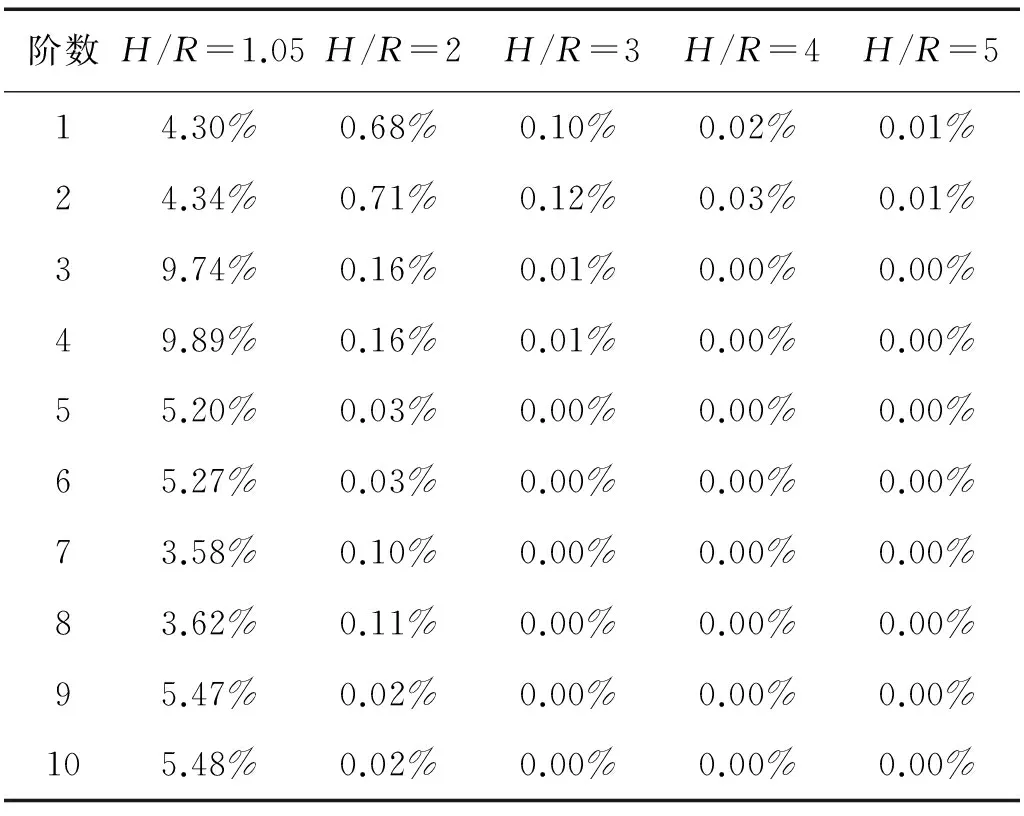
表3 不同浸没深度下各阶固有频率对应的相对偏差κ
从表3可以看出,当无量纲浸没深度H/R大于等于2时,相对偏差κ均在1%以内;当H/R大于等于4时,相对偏差κ均在0.1%以内。这也说明当浸没深度大于圆柱壳结构半径4倍及以上时,自由液面对结构振动特性的影响可以忽略不计,或者说此时自由振动特性趋于无限域。实际上随着浸没深度的增加,虚源距离实际结构越来越远,因此作用在结构外表面的虚源流体载荷也越来越小,其对水下结构振动特性的影响越来越弱,最后振动特性趋于无限域。
水下圆柱壳流固耦合振动特性分析中无量纲轴向波数kmR是较为敏感的物理量,因此本文针对无量纲浸没深度H/R为4 时不同长径比L/R下自由液面对结构振动特性的影响进行分析。半径不变,H/R=4,取长径比L/R分别为5, 10, 15, 20,分析前4阶固有频率对应的相对偏差κ的大小,如表4所示。

表4 不同长径比L/R下各阶固有频率对应的相对偏差κ
从表4可以看出,对于不同的长径比,前4阶固有频率对应的相对偏差κ都小于0.1%,因此对于不同长径比,浸没深度大于圆柱壳结构半径4倍及以上时,自由液面对结构振动特性的影响可以忽略不计。
3 结 论
基于能量泛函变分的方法和镜像原理,本文提出了一种求解有限浸没深度下圆柱壳振动特性的解析方法,和数值仿真计算结果对比表明本文方法是准确可靠的。通过对该问题的研究,得到以下三条结论:
(1) 自由液面的存在会增大同阶次模态固有频率,而且离自由液面越近,同阶次固有频率越大。
(2) 离自由液面很近时,模态振型与无限域情况有明显区别,一方面周向波相互耦合,振型不再规则,另一方面,正反模态频率出现差异。
(3) 自由液面离结构很近时对结构振动的影响才较为明显,当浸没深度大于结构半径的四倍,自由振动特性趋于无限域。
[1] 徐慕冰, 圆柱壳-流场耦合系统的振动波传播与能量流研究[D]. 武汉: 华中科技大学, 1998.
[2] ZHANG X M, LIU G R, LAM K Y. Coupled vibration analysis of fluid-filled cylindrical shells [J]. Applied Acoustics, 2001, 62(3): 229-243.
[3] ZHANG X M. Frequency analysis of submerged cylindrical shells with the wave propagation approach [J]. International Journal of Mechanical Sciences, 2002, 44(7): 1259-1273.
[4] 曹雷, 马运义, 黄玉盈. 基于Riccati传递矩阵法分析水下有限长环肋圆柱壳的声辐射性能[J]. 振动与冲击, 2009, 28(9): 149-154. CAO Lei, MA Yunyi, HUANG Yuying. Analysis of acoustic radiation of a ring-stiffened cylindrical shell with finite length in underwater based on Riccati transfer matrix method [J]. Journal of Vibration and Shock, 2009, 28(9): 149-154.
[5] 李学斌.环肋圆柱壳自由振动分析的能量法[J]. 船舶力学, 2001, 5(2): 73-81. LI Xuebin. Energy method for free vibration analysis of ring-stiffened cylindrical shells [J]. Journal of Ship Mechanics, 2001, 5(2): 73-81.
[6] ERGIN A, PRICE W G, RANDALL R, et al. Dynamic characteristics of a submerged, flexible cylinder vibrating in finite water depths [J]. Journal of Ship Research, 1992,36(2):154-167.
[7] AMABILI M. Free vibration of partially filled horizontal cylindrical shells [J]. Journal of Sound and Vibration, 1996, 191(5): 757-780.
[8] AMABILI M. Flexural vibration of cylindrical shells partially coupled with external and internal fluids [J]. Journal of Vibration and Acoustics, 1997, 119(3): 476-484.
[9] ERGIN A, TEMAREL P. Free vibration of a partially liquid filled and submerged horizontal cylindrical shell [J]. Journal of Sound and Vibration, 2002, 254(5): 951-965.
[10] 王斌,汤渭霖.半潜状态圆柱壳振动声辐射特性研究 [C]∥第十二届船舶水下噪声学术讨论会论文集.长沙, 2009.
[11] 白振国, 吴文伟, 左成魁, 等. 有限水深环境圆柱壳声辐射及传播特性[J] 船舶力学, 2014, 18(1/2): 178-190. BAI Zhenguo, WU Wenwei, ZUO Chengkui, et al. Sound radiation and spread characteristics of cylindrical shell in finite depth water [J]. Journal of Ship Mechanics, 2014, 18(1/2):178-190.
[12] LI T Y, MIAO Y Y, YE W B, et al. Far-field sound radiation of a submerged cylindrical shell at finite depth from the free surface [J]. The Journal of the Acoustical Society of America, 2014, 136(3): 1054-1064.
[13] 刘佩, 刘书文, 黎胜. 潜深对水下圆柱壳振动声辐射特性的影响[J]. 舰船科学技术, 2014, 36(5): 36-41. LIU Pei, LIU Shuwen, LI Sheng. The effects of immersion depth of submerged cylindrical shell on vibro-acoustic characteristics [J]. Ship Science and Technology, 2014, 36(5):36-41.
[14] ZHOU Q, JOSEPH P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure [J]. Journal of Sound and Vibration, 2005, 283(3): 853-873.
[15] JUNGE M, BRUNNER D, BECKER J, et al. Interface-reduction for the Craig-Bampton and Rubin method applied to FE-BE coupling with a large fluid-structure interface [J]. International Journal for Numerical Methods in Engineering, 2009, 77(12): 1731-1752.
[16] 邹明松, 吴有生, 沈顺根, 等. 考虑航速及自由液面影响的声介质中三维结构水弹性力学研究[J]. 船舶力学, 2010, 14(11): 1304-1311. ZOU Mingsong, WU Yousheng, SHEN Shungen, et al. Three-dimensional hydro elasticity with forward speed and free surface in acoustic medium [J]. Journal of Ship Mechanics, 2010, 14(11): 1304-1311.
[17] LEE W M, CHEN J T. Scattering of flexural wave in a thin plate with multiple circular holes by using the multipole Trefftz method [J]. International Journal of Solids and Structures, 2010, 47(9): 1118-1129.
Free vibration of a submerged cylindrical shell with a finite submerged depth considering the effect of free surface
GUO Wenjie1,2, LI Tianyun1,2,3, ZHU Xiang1,2, MIAO Yuyue1,2, YANG Guodong1,2
(1. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2.Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China; 3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)
An analytical method was proposed to solve the vibration characteristics of a submerged finite cylindrical shell with a finite submerged depth from the fluid free surface. Based on the image method and the Graf’s addition theorem, the analytical expression of the velocity potential of fluid was obtained. According to the energy functional variation principle, combined with the velocity potential of fluid, a fluid-structure coupling equation of the submerged finite cylindrical shell was deduced, and the natural frequencies of the shell were calculated. It is found that, with the same modal order, the natural frequency of the submerged finite cylindrical shell with the consideration of the effect of free surface is larger than that in an infinite fluid field. The natural frequency increases as the submerged depth of the finite cylindrical shell decreases. Moreover, the free vibration characteristics of the submerged finite cylindrical shell with considering the free surface tend to be the same as those without considering the free surface as the submerged depth increases. The reliability and efficiency of the present method were validated by comparing with the finite element method. The work provides more understanding on the vibration characteristics of the submerged finite cylindrical shell with finite submerged water depth.
free surface; energy functional variation; image method; Graf’s addition theorem
国家自然科学基金资助项目(51379083;51479079;51579109);高等学校博士学科点专项科研基金项目(20120142110051)
2016-01-18 修改稿收到日期: 2016-03-29
郭文杰 男,博士生,1991年11月生
李天匀 男,博士,教授,1969年2月生
U661.44
A
10.13465/j.cnki.jvs.2017.10.001
