抑制失谐星载天线振动局部化的失谐优化及控制改善

贺尔铭， 聂 良， 马小飞, 徐宏英

(1.西北工业大学 航空学院，西安 710072； 2.中国航天科技集团公司五院西安分院，西安 710100)

抑制失谐星载天线振动局部化的失谐优化及控制改善

贺尔铭1， 聂 良1， 马小飞2, 徐宏英1

(1.西北工业大学 航空学院，西安 710072； 2.中国航天科技集团公司五院西安分院，西安 710100)

为了抑制随机失谐星载天线结构的振动局部化及其导致的振动控制失效问题，建立了径向肋天线结构的单肋多自由度集中参数模型，提出了一种衡量结构整体振动模态品质的局部化因子；分析了失谐肋的安装顺序对结构整体模态振型的影响，利用遗传算法对失谐肋的安装顺序进行了减振优化，并评估了失谐优化对天线振动控制系统性能的提升。结果表明，对于一组具有特定随机失谐参数的径向肋，基于本文的模态局部化因子和智能搜索算法可以快速、准确地得到其最优或近似最优安装顺序，不仅能大大改善天线整体振动模态品质、降低结构振动响应，还能提高天线结构控制系统效能。

径向肋天线；随机失谐；振动局部化；智能算法；减振

理想星载天线结构为典型循环周期结构，但制造误差、运行磨损等因素会导致各子结构间存在小量偏差，这种情况称为结构失谐。失谐会使结构的振动能量集中在少数几个子结构上，即产生结构的振动局部化，包括模态局部化和响应局部化，这两者很可能会造成天线结构破坏及相应振动控制系统鲁棒性丧失等一系列问题[1-2]。随着天线结构尺寸的增加，失谐对其整体性能的影响将更加突出。迄今为止，国内外学者们为了解决这一问题进行了许多比较深入的研究。Dosch等[3]基于失谐缠绕肋天线结构的简化模型研究了天线的PPF(Positive Position Feedback)控制和H∞鲁棒控制问题。Zee等[2]基于典型失谐柔性空间天线结构的特征值摄动模型采用集中控制方法研究了天线的振动控制问题。在国内，刘相秋等[4]也基于失谐缠绕肋天线结构的有限元简化模型采用预测控制方法对失谐天线结构进行了振动主动控制。这些研究虽然都取得了较好的控制效果，但大多集中在结构振动的主动控制方面，其控制器的设计也要远比谐调系统复杂，这会额外增加系统的能源、重量及结构的复杂性，对于日益要求轻量化的航天器来说显然是一个不小的负担。

本文结合模态价值分析理论提出一种可以衡量结构整体振动模态品质的局部化因子，从结构优化设计的角度出发，分析失谐肋的安装顺序对天线结构整体振动模态振型的影响，利用遗传算法优化失谐肋的安装顺序，从而改善失谐结构的整体振动模态品质，从根本上抑制失谐天线结构的振动局部化，提高天线结构控制系统效能。

1 天线结构的模型建立

本文研究的径向肋可展开天线由18根径向肋、缠绕在肋上的20圈周向预应力拉索、金属反射网以及位于中心的刚性底座四部分组成，中心底座周边固定约束。将金属反射网的质量均匀分配给两边的径向肋而不考虑其受力特性。建立的天线结构有限元模型如图1(a)所示，其单肋扇区的多自由度集中参数模型如图1(b)。

假设所有径向肋都直接固定在中心刚性底座上，将单肋扇区中肋的等效质量用集中质量m1～m4表示；肋的等效弯曲刚度用k1～k4表示；肋间周向拉索的耦合刚度用kcp1～kcp4表示，由于周向拉索的质量相对肋质量很小，因此将其质量均布到径向肋集中质量上。

(a) 有限元模型

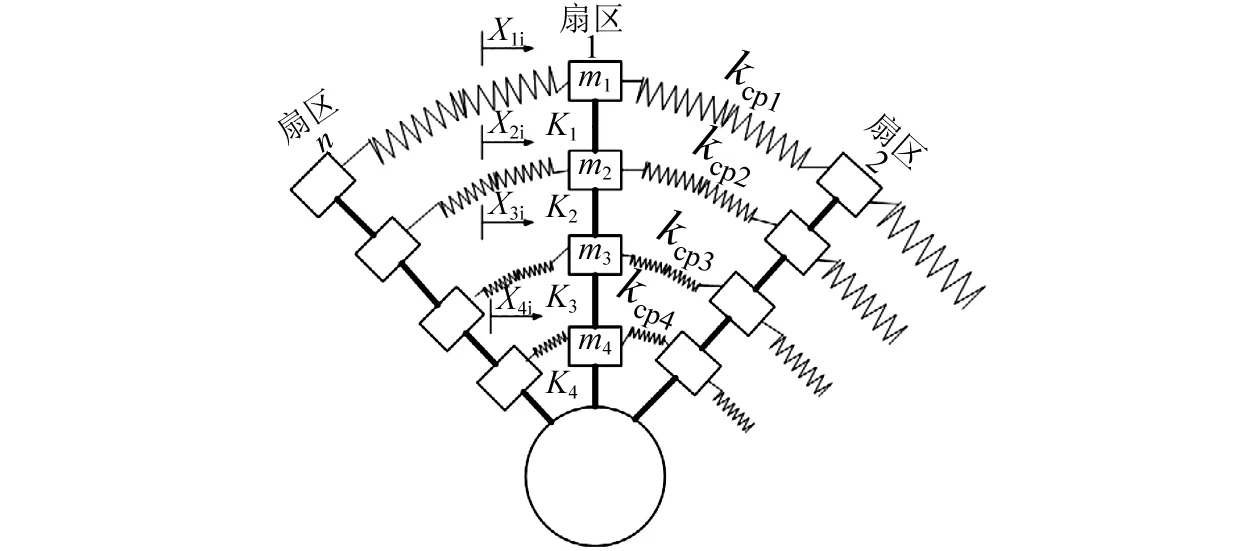
(b) 基于单肋扇区多自由度的集中参数模型图1 径向肋天线结构简化模型Fig.1 The simplified model of the radial rib antenna

简化后的集中参数模型如图1(b)所示，该模型不仅将细长径向肋等效为多质量-弹簧系统，而且考虑了不同肋高处横向拉索的耦合刚度差异，因此该模型能更准确地模拟天线结构的真实力学特性。天线集中参数模型的动力学方程：

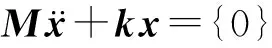
(1)

其中，

x=[x11,x12,…,x1n,x21,x22,…,x2n,x31,x32,…,x3n,x41,x42,…,x4n]T

其中，

A=circ(k1+2kcp1,-kcp1,…，-kcp1)

B=circ(k1+k2+2cp2,-kcp2,…，-kcp2)

C=circ(k2+k3+2kcp3,-kcp3,…，-kcp3)

D=circ(k3+k4+2kcp4,-kcp4,…，-kcp4)

求解式(1)的特征值问题就会得到天线结构的各阶固有频率及相应的模态振型。

根据有限元模型，在天线的径向肋上施加单位位移，根据相应的等效力可以确定各等效刚度，等效质量可以通过对应的材料密度及体积确定。最后根据天线整体结构的固有特性(模态振型和固有频率)及总质量修正各参数，最终确定本文所研究的谐调天线结构的集中参数模型各参数取值如图2和表1所示。

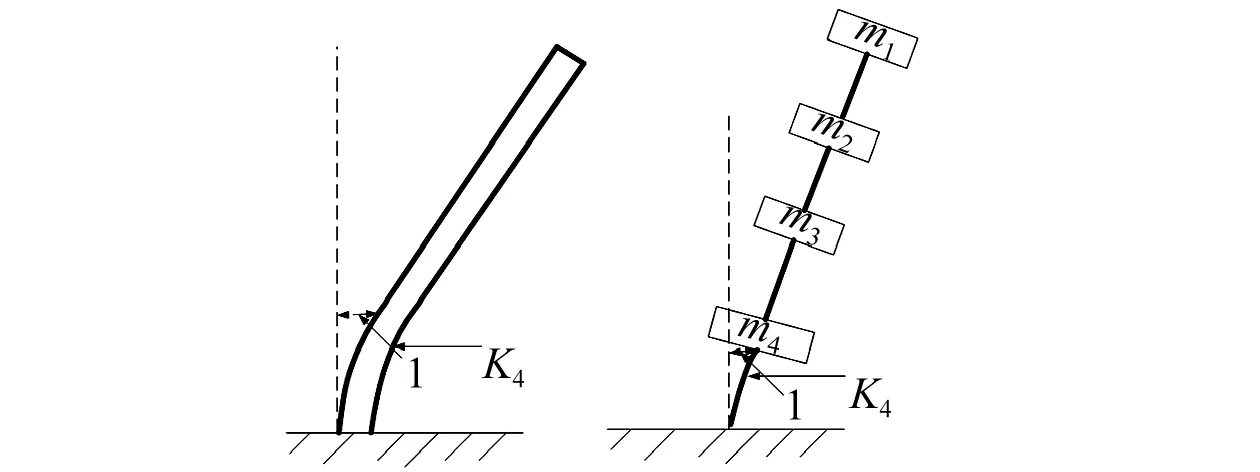
图2 集中参数模型的参数确定Fig.2 The estimation of model parameters

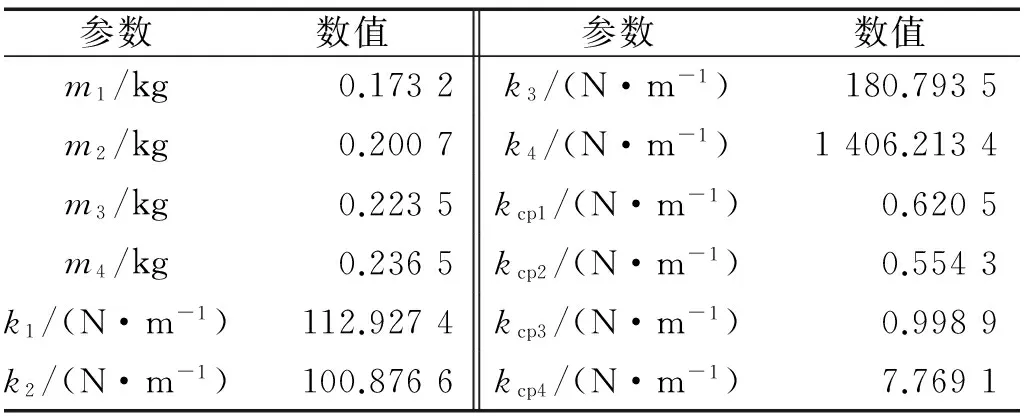
参数数值参数数值m1/kg0.1732k3/(N·m-1)180.7935m2/kg0.2007k4/(N·m-1)1406.2134m3/kg0.2235kcp1/(N·m-1)0.6205m4/kg0.2365kcp2/(N·m-1)0.5543k1/(N·m-1)112.9274kcp3/(N·m-1)0.9989k2/(N·m-1)100.8766kcp4/(N·m-1)7.7691

2 失谐肋排列对天线振动局部化的影响

以往的叶盘系统研究中，只关注于采用叶片位置的优化设计来抑制失谐叶盘系统的振动响应，事实上，振动响应最小的安装顺序其振动模态局部化往往不是最小，反而有可能比较大[5]。由于太空中天线所受载荷的复杂性，对于结构的振动抑制，完全不采用主动控制的方法显然是不现实的，因此，必须采用一种结构优化设计的方法使失谐天线结构的振动响应得到抑制的同时改善结构的整体振动模态振型。针对以往研究中所提出的振动模态局部化因子只能衡量某一阶模态的情况，本文结合模态价值分析理论[6]提出一种可以衡量结构整体振动模态品质的局部化因子L

(2)

其中单阶模态局部化因子L0[7]为：

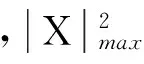
其中，i=1,…,n为模态阶数，nu和ny分别为输入输出自由度数，bj、cl和gl分别为输入输出矩阵系数，ωi、φi、mi和ξi分别为第i阶固有频率、模态振型、模态质量和阻尼系数。c由系统本身动力学特性和输入输出特性唯一决定。

假设只存在径向肋刚度失谐，任意选取一组期望为0，标准差σ=0.01的服从均匀分布的随机数δi(i=1,2,…,18)，刚度失谐量为kjiδi(i=1,2,…,18,j=1,2,3,4)，质量失谐及耦合刚度失谐时的取值与此类似。权重系数m取3，不同的失谐肋安装顺序的局部化因子L如表2所示。在质量块m4i(i=1,2,…,18)上同时加载一幅值1 N，脉冲宽度0.1 s的均布瞬态冲击载荷，阻尼取瑞利阻尼C=5.9×10-3K+1×10-3M[8]。失谐对天线结构受迫振动响应幅值的放大影响用振幅放大因子AMF[7]表示为：

(3)

图3为三种失谐径向肋安装形式下天线结构的各阶模态局部化因子L0，排列1为失谐天线结构响应最大时的安装形式，排列2为失谐天线结构响应最小时的安装形式，排列方式1、2、3对应的整体模态局部化因子L分别为1.983 7、1.151 0、1.089 3，各排列方式的局部化因子L与其各阶模态局部化因子L0基本成正比关系，特别是模态价值较高的模态(第55、72、61、67阶等)，这说明本文提出的局部化因子L能准确衡量结构的整体振动模态局部化程度，且失谐天线结构的振动模态局部化程度与其径向肋安装顺序密切相关。

表2 不同失谐径向肋的安装顺序及其振动局部化因子

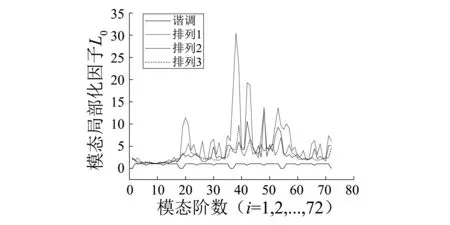
图3 不同失谐径向肋排列的局部化因子L0Fig.3 The localization factor L0 of different mistuned ribs arrangements

从图3、4中还可以看出结构响应幅值最小并不意味着其整体模态局部化最小，但是整体模态局部化较小，其对应的响应幅值一定较小。因此，可以通过优化天线结构失谐肋安装顺序的方法减小其整体模态局部化，从而到达改善其控制系统的设计同时抑制结构响应的目的。

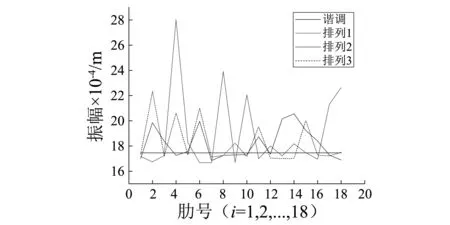
图4 不同失谐径向肋排列的各肋最大响应幅值Fig.4 The maximum response amplitude of the ribs of the different mistuned ribs arrangements

3 天线结构失谐肋安装顺序的优化方法

天线结构径向肋安装顺序的优化排列问题是一个组合优化问题，对于径向肋数目较多的情况，会产生搜索组合的爆炸。遗传算法是一种随机全局搜索和优化方法，适用于处理传统优化方法难以解决的复杂的非线性优化问题[9]。

本文选取遗传算法的种群大小为50，交叉概率Pc为0.65，变异概率Pm为遗传世代数g的指数函数形式[10]，Pm(g)=Pm(0)exp[-τg/gmax]，其中初始变异概率Pm(0)为0.90，τ=5。以n根径向肋的遍历次序作为遗传算法的编码[11]；由于天线结构模态局部化因子L越小则安装顺序越好(L>0)，因此适应度函数可以选取为1/L；选择方法采用轮盘赌选择和最优保留选择策略；交叉采用部分匹配交叉方法；变异采用逆转变异方法；终止条件：进化代数取值为500，将每一次进行指定代数运算后得到的最优解精英保留更新到初始种群中重复计算，直到最优解不再发生变化为止[12]。

4 典型天线结构算例

4.1 失谐肋安装顺序的优化

应用上述优化方法对天线结构失谐肋的安装顺序进行优化，优化结果如表3所示。

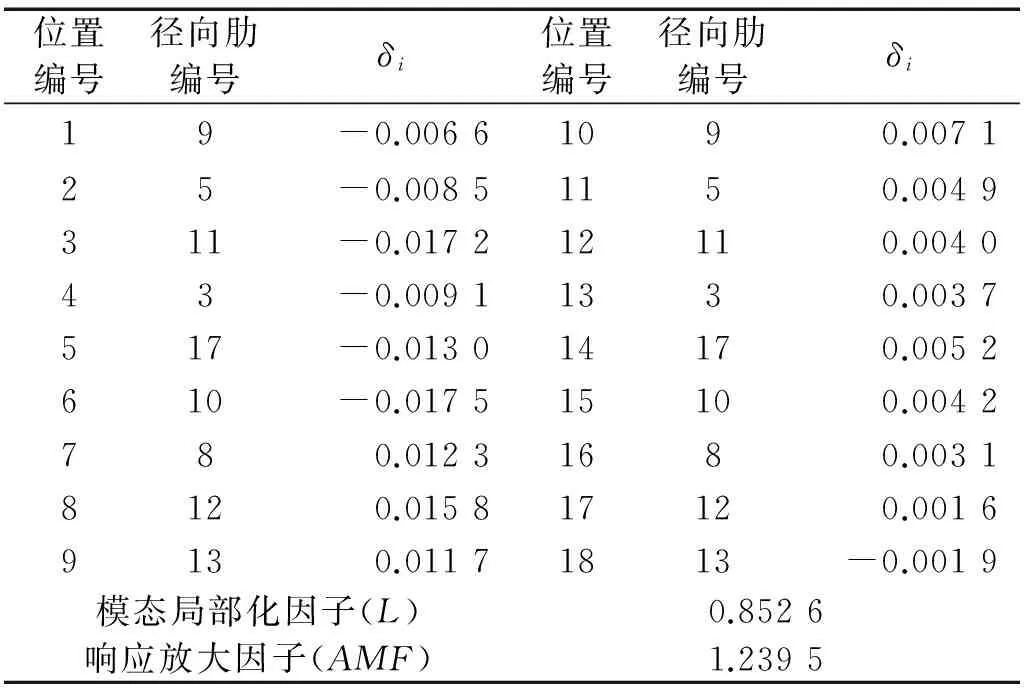
表3 天线结构优化后的安装方案

优化前后失谐天线结构的各阶模态局部化因子如图5所示，可以看到优化前结构的各阶振动模态特别是中高阶模态的局部化都比较严重，整体振动模态局部化因子L高达1.983 7，单阶模态局部化因子甚至高达30.5(第38阶)；优化后整体振动模态局部化因子L降低为0.852 6，振动模态局部化程度降低了57%，单阶模态局部化因子最高只有7.5(第41阶)；且优化后局部化因子L0比较大的模态(第35～45、52～54、20～25阶等)均为模态价值较小的模态，这说明优化后的径向肋安装顺序可以有效地抑制失谐天线结构的整体振动模态局部化。

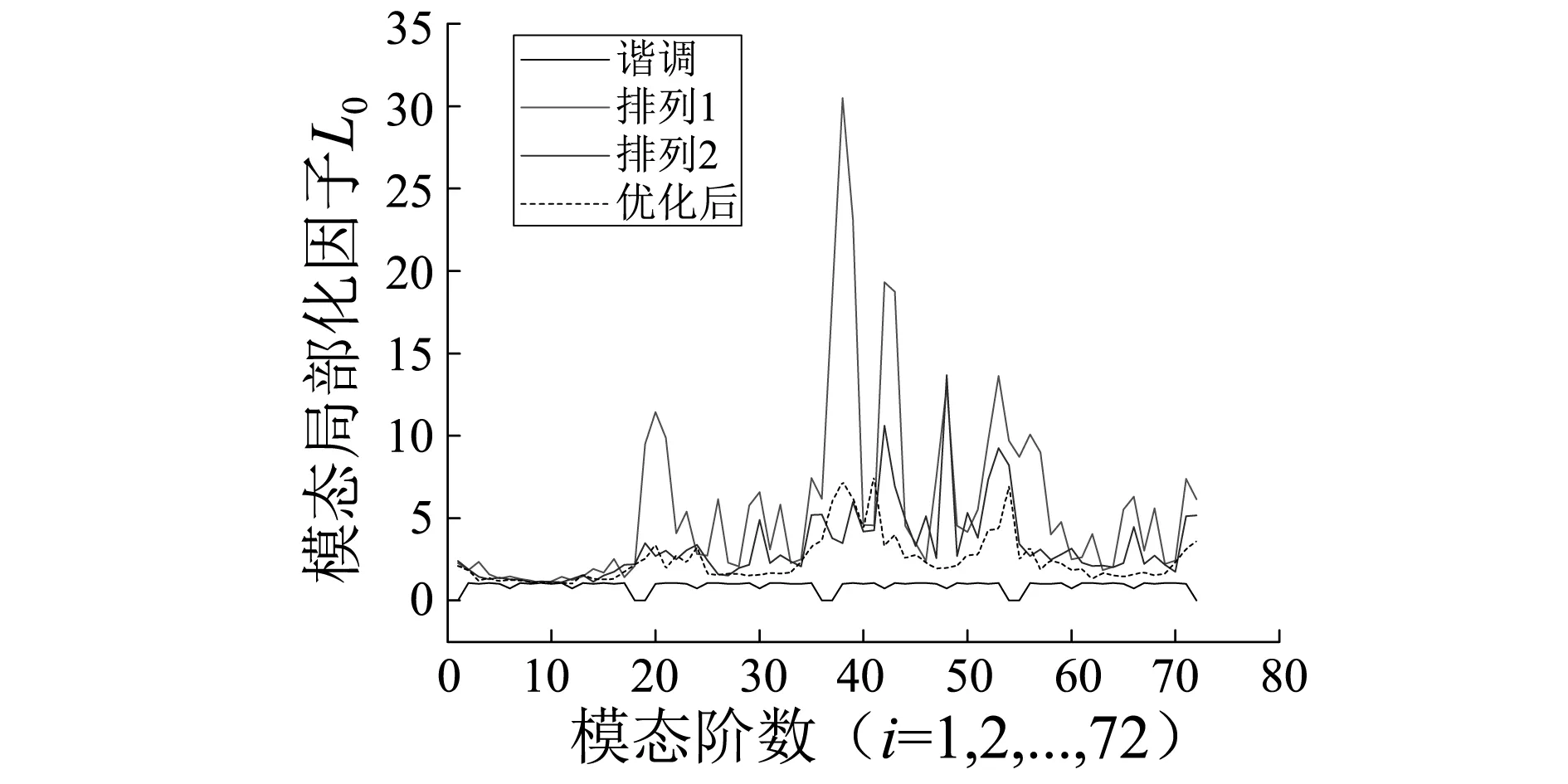
图5 不同径向肋排列天线结构的局部化因子L0Fig.5 The localization factor L0 of different mistuned ribs arrangements

从图6中可以看出，按照本文方法优化后结构的最大振动响应幅值相对于优化前减少了23%，虽然响应幅值比排列方式2(即最小响应安装形式)略大了5%，但其整体模态局部化相比降低了26%，特别是在第28～35、42～55、60～72阶模态降低幅度更大；且优化后除了第3、5、6号肋，其余肋的最大响应幅值都得到了降低或只有小量增加，因此优化后的安装形式对于结构的振动响应也有极大的抑制作用。

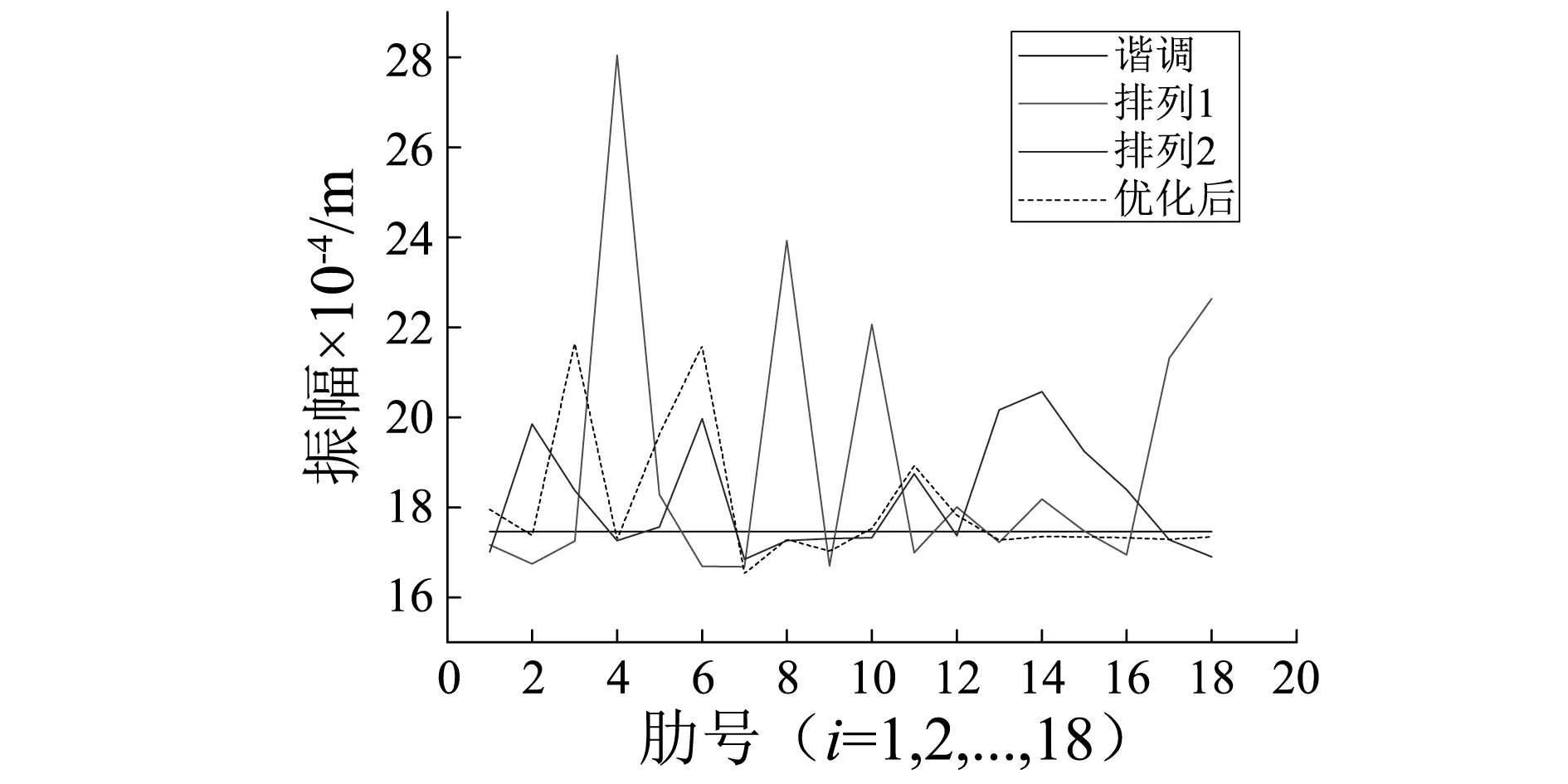
图6 不同径向肋排列天线结构各肋最大响应幅值Fig.6 The maximum response amplitude of the ribs of the different mistuned ribs arrangements

4.2 失谐肋安装顺序对振动控制系统影响

文献[13]中关于失谐卫星碟型天线结构的振动LQR控制研究表明：失谐会导致控制系统的失效，甚至引入激振。为了分析本文采用的优化方法对于失谐天线结构振动控制系统的影响，这里同样采用基于模态空间的LQR算法[14]对结构进行振动控制。系统动力学方程的一般形式可以写成

(4)

式中：C为结构阻尼矩阵；F为外界激励力；Bf为控制力的位置矩阵;u控制力矩阵。

模态坐标向量q(t)、节点位移向量x和模态矩阵Φ之间的关系为

x=Φq(t)

(5)

根据模态的正交性, 将系统的动力学方程式(4)解耦，可得：

ΦTKΦq(t)=ΦT(M+Bu)

(6)

将式(6)转化成状态方程的形式，

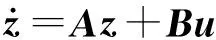
(7)

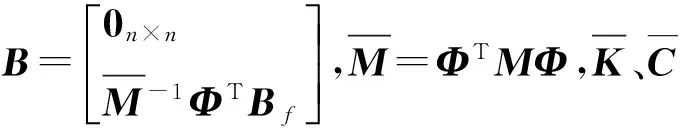
由LQR算法定义系统的二次型性能泛函为

(8)

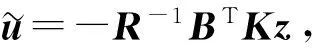
KA+ATK-KBR-1BTK-Q=0

(9)

考虑与第2节中排列方式2相同失谐与加载情况的天线结构，取1号肋顶端的位移响应进行分析，优化前后结构的控制效果如图7～9，控制力如图10。

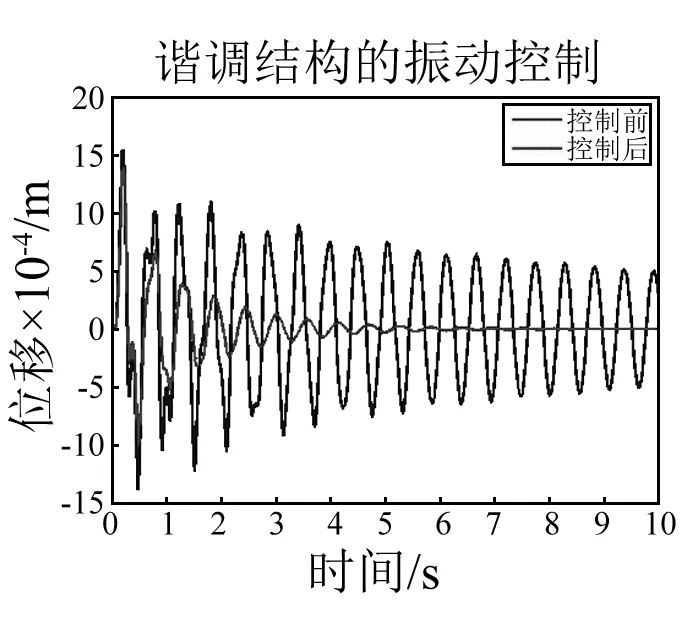
图7 谐调天线结构振动控制前后的响应Fig.7 The response of tuned antennabefore and after vibration control

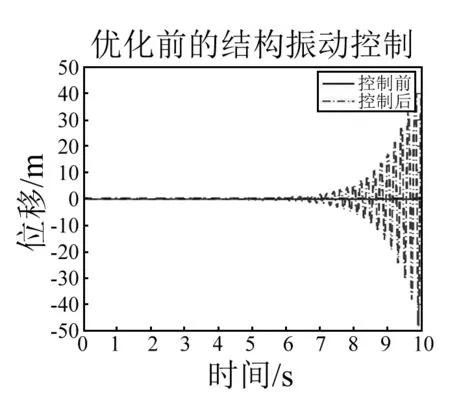
图8 优化前失谐天线结构振动控制前后的响应Fig.8 The response of un-optimized mistuned antenna before and after vibration control

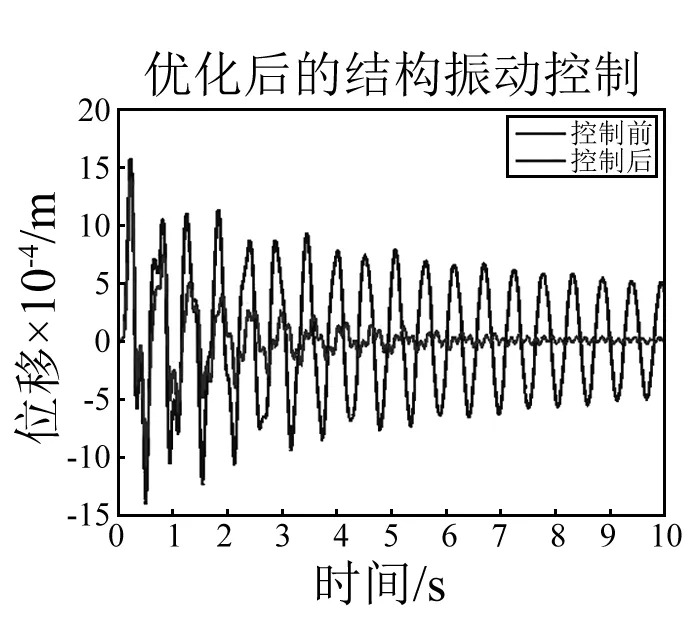
图9 优化后失谐天线结构振动控制前后的响应Fig.9 The response of optimized mistuned antenna before and after vibration control

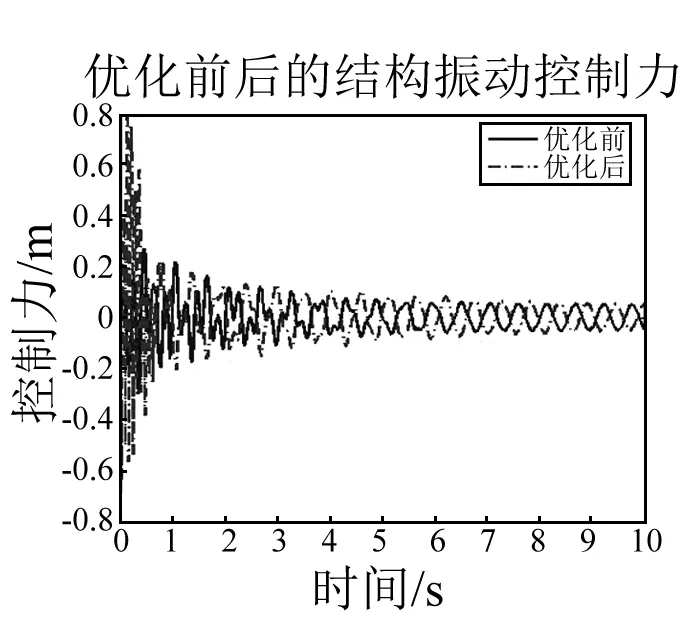
图10 优化前后失谐天线结构的振动控制力Fig.10 The control force of mistuned antenna before and after optimization

从图7、8、10可以看出：对失谐天线结构进行振动控制时，如果控制器的设计不考虑失谐对于结构带来的影响，则控制系统非但不能控制结构的振动，反而较小的控制力就会产生较大的激振，不到10 s结构的振动响应就产生了发散。从图9中可以看出：采用本文的优化方法对失谐肋的安装顺序进行排列优化后，失谐对结构振动控制带来的不利影响被极大地削弱了，采用常用的LQR算法设计的控制器已经能很好地抑制结构的振动，6 s内结构振动响应幅值降低到控制前的5%。

5 结 论

本文建立了径向肋天线结构的集中参数模型，以模态局部化因子衡量结构的动力学性能，分析了随机失谐肋的安装顺序对结构整体振动模态振型的影响，利用遗传算法优化了失谐肋的安装顺序，并评估了失谐优化对天线振动控制系统性能的提升。研究结果表明：

(1)失谐天线结构的整体振动模态品质可以通过径向肋安装顺序的优化来改善，利用遗传算法的全局收敛特性及内在并行性能够快速、准确地找到有效抑制失谐天线结构振动局部化的安装顺序。

(2)本文采用的优化方法可以从根本上抑制失谐天线结构的振动局部化现象，振动模态局部化降低了57%，响应幅值减小了23%。

(3)失谐会导致天线结构振动控制系统失效，不到10 s结构的振动响应就产生了发散；优化后结构的振动控制系统效能得到了有效地提升，振动响应幅值在6 s内降低到控制前的5%。

对于其它类似的失谐周期结构，本文提出的模态局部化因子及采用的优化方法同样适用。本文采用的优化方法对改善失谐星载天线结构控制系统的设计及振动的抑制具有重要意义。考虑到天线结构的失谐具有随机性，今后将着重探索随机失谐径向肋的安装顺序与整体模态品质之间的一般性统计规律，以便于本文方法的实际应用。

[1] LEVINE-WEST M B, SALAMAT M A. Mode localization experiments on a ribbed antenna [J]. AIAA, 1993, 31(10):1929-1937.

[2] ZEE R E, HUGHES P C. Mode localization in flexible spacecraft:a control challenge [J].Guidance,Control,and Dynamics, 2000, 23(1):69-76.

[3] DOSCH J, LEO D, INMAN D. Modeling and control for vibration suppression of a flexible active structure[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(2): 340-346.

[4] 刘相秋, 王聪, 邹振祝. 弱耦合星载天线结构振动神经网络预测控制[J]. 哈尔滨工业大学学报, 2010 (3): 373-377. LIU Xiangqiu, WANG Cong, ZOU Zhenzhu.Vibration control of weak coupling antenna structure in statellite by neural networks predictive method[J]. Journal of Harbin Institute of Technology, 2010 (3): 373-377.

[5] 王锋, 唐国金, 李道奎. 基于模态价值分析的结构动力学模型降阶[J]. 振动与冲击, 2006, 25(3):35-39. WANG Feng, TANG Guojin, LI Daokui. Order reduction for structural dynamic modeling model value analysis[J]. Journal of Vibration and Shock, 2006, 25(3):35-39.

[6] RIVAS-GUERRA A J, MIGNOLET M P. Local/global effects of mistuning on the forced response of bladed disks[J]. Journal of Engineering for Gas Turbines and Power, 2004, 126(1): 131-141.

[7] 王红建, 贺尔铭, 赵志彬. 频率转向特征对失谐叶盘模态局部化的作用[J].中国机械工程，2009,10(1):82-85. WANG Hongjian, HE Erming, ZHAO Zhibin. Effects of frequency veering features on mode localization of mistuned bladed disks[J]. China Mechanical Engineering, 2009,10(1):82-85.

[8] 高军虎. 展开天线结构动力学和振动控制分析[D]. 杭州：浙江大学, 2012.

[9] RAHIMI M, ZIAEI-RAD S. Uncertainty treatment in forced response calculation of mistuned bladed disk[J]. Mathematics & Computers in Simulation, 2010,80(8): 1746-1757.

[10]CHOI B K. Pattern optimization of intentionnal blade mistuning for the reduction of the forced response using genetic algorithm[J]. Journal of Mechanical Science and Technology, 2003, 17(7): 966-977.

[11] 杨训, 邢建华. 基于遗传算法的转子叶片优化排序[J]. 计算机仿真, 2008, 25(11):94-97. YANG Xun, XING Jianhua. Optium arrangement of rotor blades based on genetic algorithm[J]. Computer Simulation, 2008, 25(11):94-97.

[12] 袁惠群, 张亮, 韩清凯. 航空发动机转子失谐叶片减振安装优化分析[J]. 振动：测试与诊断, 2011, 31(5):647-651. YUAN Huiqun， ZHANG Liang， HAN Qingkai. Reducing vibration mounting optimization for aero-engine rotor mistuned blade[J]. Journal of Vibration, Measurement & Diagnosis，2011，31(5):647-651.

[13] 刘相秋, 王聪, 邹振祝. 考虑失谐的弱耦合周期天线结构的振动主动控制研究[J]. 振动与冲击, 2009, 28(6):126-130. LIU Xiangqiu, WANG Cong, ZOU Zhenzhu. The study on active vibration control of weak coupling periodic antenna structure Considering disorder[J]. Journal of Vibration and Shock, 2009, 28(6): 126-130.

[14] 符川, 屈铁军, 孙世国. 主动调频液柱阻尼器基于遗传算法的LQR控制优化设计[J]. 振动与冲击, 2015, 29(2):206-211. FU Chuan，QU Tiejun，SUN Shiguo. Optimal design of ATLCD with LQR control based on genetic algorithm[J]. Journal of Vibration and Shock, 2015, 29(2):206-211.

Optimization of mistuning for the vibration localization reduction andcontrol system improvement in a mistuned space-borne antenna

HE Erming1，NIE Liang1， MA Xiaofei2， XU Hongying1

(1. School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2. CAST-Xi’an Institute of Space Radio Technology, Xi’an 710100, China)

To suppress the vibration localization and improve the vibration control system of mistuned space-borne antenna structures, a single rib multi-freedom lumped parameters model for the radial rib antenna was established. A mode localization factor for measuring the overall quality of structural vibration modes was proposed. The influence of certain mistuned ribs arrangements of the antenna on the overall structural vibration modes was studied. The optimal design of the mistuned ribs arrangement was performed by using the genetic algorithm (GA), and the effect of optimization of the mistuned ribs arrangement on enhancing the performance of vibration control system was assessed. The results show that: for a group of random mistuned ribs, the optimal or approximate optimal mistuned ribs arrangement can be quickly and accurately obtained by the genetic algorithm and mode localization factor proposed in the paper, and the optimal mistuned ribs arrangement can not only greatly improve the overall quality of structural vibration modes and reduce the structural vibration response, but also improve the efficiency of the vibration control system of the antenna.

radial rib antenna; random mistuning; vibration localization; intelligent algorithm ; vibration reduction

国家自然科学基金(51675426)；航天科技创新基金项目(2014KC010043)

2015-07-15 修改稿收到日期： 2016-03-29

贺尔铭 男，博士，教授，1964年3月生

聂良 男，硕士生，1991年2月生

O327; V414.9

A

10.13465/j.cnki.jvs.2017.10.008