考虑撬棒保护的DFIG等效序阻抗研究

黄 涛 陆于平 王 业

(1.东南大学电气工程学院 南京 210096 2.江苏省电力公司 南京 210024)



考虑撬棒保护的DFIG等效序阻抗研究

黄 涛1陆于平1王 业2

(1.东南大学电气工程学院 南京 210096 2.江苏省电力公司 南京 210024)

双馈感应风力发电机(DFIG)等效序阻抗特征对基于故障分量的继电保护原理影响重大。针对目前DFIG等效序阻抗理论分析及暂态变化过程研究的欠缺，首先给出了DFIG等效序阻抗的定义，考虑故障后投入撬棒保护这一情况，基于DFIG定子故障序电流推导了等效序阻抗的解析表达式。然后详细研究了DFIG等效正、负序阻抗的特征及其影响因素，指出等效正序阻抗有明显的暂态变化过程，其幅值较大且有波动，稳态相角在-90°～-180°之间；等效负序阻抗暂态过程不明显，其幅值较小，相角在0°～90°之间。最后通过仿真实验验证了理论分析的正确性。

双馈感应风力发电机 撬棒保护 等效序阻抗 幅值和相角 暂态变化特征

0 引言

双馈感应风力发电机(Doubly Fed Induction Generator，DFIG)是目前风力发电机组的主流机型，采用异步发电机和电力电子装置相结合的特殊结构，其故障暂态特性与同步发电机存在较大差异[1-5]，给传统继电保护装置的正常工作造成了重大影响[6-9]。

故障分量能够快速准确地反映出故障，广泛应用于继电保护原理中，如基于故障分量的方向元件、选相元件和距离元件等。但是在这些保护原理中，往往要求故障附加网络中各元件的正、负序阻抗相等[10，11]，否则会严重影响保护的动作性能。传统电力系统中，各元件正、负序阻抗近似相等，且同步发电机暂态电势在故障前后基本不变，满足故障附加网络中各元件正、负序阻抗相等的条件。但当风力发电接入电网后，该条件受到了挑战，随着DFIG故障特性研究的不断深入，一些文献指出DFIG的正、负序阻抗并不相等：文献[11]从DFIG内电势故障前后不能保持恒定的角度，结合仿真和现场录波数据指出DFIG的正、负序阻抗不相等；文献[12，13]基于异步电机的稳态序阻抗表达式研究了DFIG投入撬棒保护后的正、负序阻抗特征，同样得出DFIG正、负序阻抗不相等的结论。

从上述文献来看，虽然对DFIG正、负序阻抗的研究已有一些初步成果，但仍存在一些不足：首先，基于仿真和录波数据得到的结论缺乏理论支撑，没有给出DFIG序阻抗的解析表达式，不清楚其对保护的影响程度有多大、与何种因素有关，不利于保护动作性能的分析及改进方案的研究；其次，缺乏DFIG序阻抗暂态变化过程的研究，基于故障分量的保护元件一般利用故障后1～2个周波内的数据进行计算，所以故障后短时间内阻抗的暂态特征对继电保护的分析尤为关键。

针对目前DFIG序阻抗理论分析及暂态变化特征研究的空缺，本文首先给出了DFIG等效正、负序阻抗的定义，在推导DFIG正、负序故障电流的基础上，得到DFIG故障后投入撬棒保护这一工况下等效正、负序阻抗的解析表达式，并详细研究了等效正、负序阻抗的暂态变化特征，为相关继电保护原理的分析提供理论依据。

1 DFIG等效序阻抗的定义

基于故障分量的继电保护原理是在故障附加网络中设计的，因此正、负序阻抗相等的要求也应该是针对故障附加网络。传统电网中各元件自身的正、负序阻抗近似相等，同步发电机的暂态电势故障前后基本不变，根据叠加定理，故障附加网络只在故障点存在一附加电势，其他电源都接地且满足各元件正、负序阻抗相等的要求。但是DFIG不同于同步发电机：首先，DFIG不存在故障前后恒定不变的暂态电势[11，14]；其次，DFIG含有非线性的电力电子装置，叠加定理不一定适用。因此接入了DFIG的系统不具备传统故障附加网络的特点，难以给出故障附加网络中DFIG正、负序阻抗的具体形式。但对于基于故障分量的继电保护来说，目前依然采用传统故障分量的提取算法，所以保护所感受到的DFIG正、负序阻抗可以分别表示为

Zw+=Δuw+/Δiw+

(1)

Zw-=uw-/iw-

(2)

式中，Δuw+、Δiw+和uw-、iw-分别为DFIG出口正序和负序电压、电流故障分量，本文规定流入风机作为电流正方向。

图1为Zw+、Zw-的图形解释，显然，Zw+、Zw-并不是DFIG自身的正、负序阻抗，而是与DFIG故障前后运行状态有关的一个虚拟阻抗，本文称之为等效正、负序阻抗。用Zw+、Zw-等效之后，DFIG在故障附加网络中的表现形式即为一接地的阻抗。

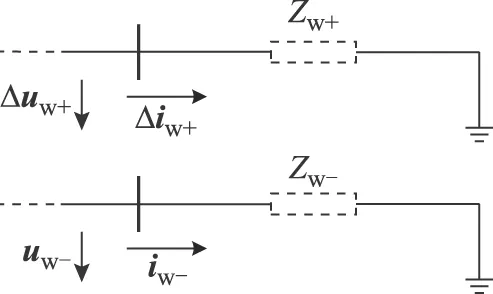
图1 Zw+与Zw-的定义图解Fig.1 Illustration of the definition of Zw+ and Zw-

Zw+、Zw-的暂态变化特征对基于故障分量保护的性能研究至关重要，从式(1)和式(2)知，等效正、负序阻抗的计算需要先求出DFIG出口的正、负序故障电流。

2 投撬棒后DFIG正、负序故障电流推导

为了提高电力系统暂态稳定性，要求DFIG具有一定的低电压穿越(LowVoltageRideThrough，LVRT)能力，根据电压跌落程度目前DFIG主要通过撬棒保护[15]或改善控制策略[16，17]来实现LVRT。这两种方式下DFIG等效序阻抗的表现形式及特征有明显区别，限于篇幅，本文只针对电压严重跌落投入撬棒保护这一情况进行分析。

由于DFIG检测到故障并投入撬棒的时间非常短，仅需几毫秒[18]，为了简化分析，假设故障后撬棒瞬时投入。另外，在故障后短时间内的电磁暂态过程中不考虑DFIG转速的变化。按照电动机惯例，选择q轴超前d轴90°，正、反向dq同步旋转坐标系下DFIG的正、负序空间矢量模型分别为[19]

(3)

(4)

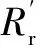
对式(3)的正序空间矢量模型进行拉氏变换,即

(5)

式中，U(p)、I(p)和Ψ(p)分别为相应电压、电流和磁链空间矢量的象函数；ψs|0|、ψr|0|分别为故障前定、转子磁链的初始值；p为拉氏算子。

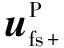
(6)

将式(6)代入式(5)消去定、转子磁链和转子电流得到定子正序电流。

(7)

式中，p1=p+jωs；p2=p+jsωs。

设故障前的定子电压、电流初始值为us|0|、is|0|。对于采用定子电压定向控制的DFIG来说，定子正序电压中始终只有d轴分量，标幺值下有

us|0|=usd|0|=1

(8)

(9)

式中，k为故障后的定子正序电压大小。

稳态运行时DFIG定子输出有功、无功功率为

(10)

DFIG一般采用最大功率追踪控制，正常运行不输出无功功率，即isq|0|=0，定子电流初始值为

is|0|=isd|0|+jisq|0|=-Ps|0|

(11)

另外稳态时式(3)中定、转子磁链微分项为零，不计定、转子电阻，可推得定、转子磁链初始值为

(12)

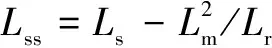
忽略数值很小的定子电阻，结合式(8)～式(12)对式(7)进行拉式反变换，求出正序故障电流为

(13)

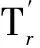
(14)

(15)

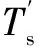
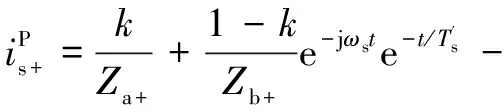
(16)

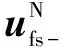
(17)

其中

(18)

(19)

由于网侧变换器提供的电流相对于定子电流很小，而且撬棒保护动作的同时一般会闭锁网侧变换器，可以近似认为DFIG出口的短路电流全部由定子短路电流提供[20]。

3 DFIG等效序阻抗表达式及特征分析

3.1 等效正序阻抗分析

(20)

由式(1)计算DFIG的等效正序阻抗为

(21)

将式(8)、式(9)、式(11)及式(20)代入式(21)得

(22)

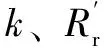
式(22)比较复杂，直接用来研究Zw+的特征很困难，但可借助空间矢量图进行分析。令

(23)

由式(21)可知，Δus+=k-1、Δis+=Δis++iD。Δus+与Δis+的比值即为Zw+，当电压跌落一定时，Δus+为固定值，Zw+的特征完全由Δis+决定。要作出Δis+的矢量图还需知道Za+、Zb+的特征。图2基于表1中参数给出了Za+随变化的幅值和相角特征为标幺值，下同)。由于Za+中s换成s-1即为Zb+，所以Za+中s在[-1.3,-0.7]的区段即为s∈[-0.3, 0.3]时Zb+的波形。

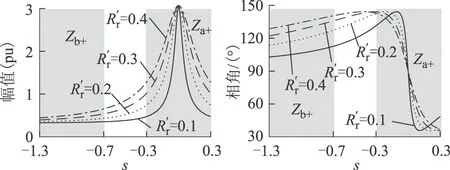
图2 Za+与Zb+的幅值相角特征Fig.2 Amplitude and angle characteristics of Za+ and Zb+

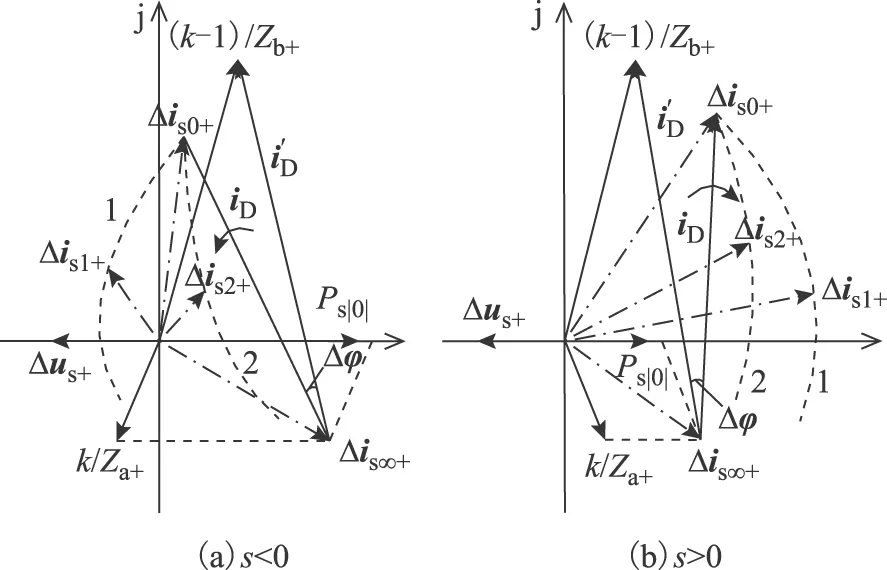
图3 Zw+的暂态变化过程分析Fig.3 Transient change process analysis of Zw+

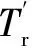
暂态变化过程：Zw+的暂态变化过程由衰减转差分量iD决定。s<0时，iD逆时针旋转，如果投入的撬棒电阻较小，iD将沿着图3a中轨迹1缓慢衰减，Δis+从Δis0+向左边旋转(如图中的Δis1+)，Zw+的相角从初相角不断减小；如果撬棒电阻较大，iD将沿着轨迹2迅速衰减，Δis+从Δis0+向右边旋转(如图中的Δis2+)，Zw+的相角从初相角逐渐增大；而整个过程Δis+的幅值变化明显，将引起Zw+幅值的剧烈波动。s>0时，iD顺时针旋转，此时无论投入撬棒电阻阻值的大小，Δis+都将从Δis0+向右边旋转，Zw+的相角均朝增大的方向变化，与s<0不同的是，Zw+的幅值虽然也会波动，但波动幅度要比s<0时小得多。s=0时，iD不旋转只衰减，Δis+从Δis0+沿着iD变化到Δis+，容易得出Zw+的相角特征与s>0时类似，其幅值将先增大后减小。

稳态：iD衰减到零后，Δis+=Δis+，Zw+的稳态表达式为Zw+=(k-1)/(k/Za++Ps|0|)。图4为不同值下Zw+随s的变化特征，其中Ps|0|与s的关系参考文献[21]中的Fig.6。从图中看到，不同参数下Zw+的幅值变化范围很大，而Zw+的相角始终在-90°～-180°。

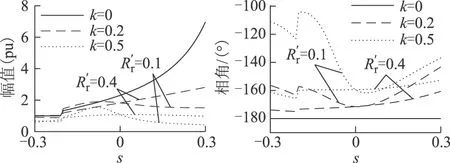
图4 Zw+的幅值相角特征Fig.4 Amplitude and angle characteristics of Zw+

综上所述，撬棒保护的投入改变了DFIG的运行状态，使得故障后DFIG等效正序阻抗的初始值和稳态值出现较大差异，而转差的存在和较大的撬棒电阻又加速了Zw+从初始值到稳态值的过渡过程，导致故障后DFIG的等效正序阻抗呈现与传统同步发电机完全不一样的特征，总结如下：

1)幅值。Zw+的幅值随电压跌落程度、投入撬棒电阻及运行转差的不同在很大范围内变化，不是一个固定值；故障后的暂态过程中Zw+的幅值会出现明显波动，且s<0时比s>0时波动更剧烈。

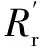
3.2 等效负序阻抗分析

(24)

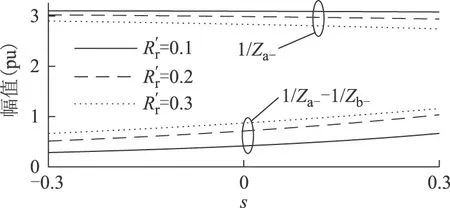
图5 (2-s)ωs频率分量与直流分量大小比较Fig.5 Comparison of(2-s)ωsand DC components

根据式(2)，DFIG的等效负序阻抗为

(25)

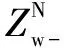
(26)

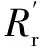
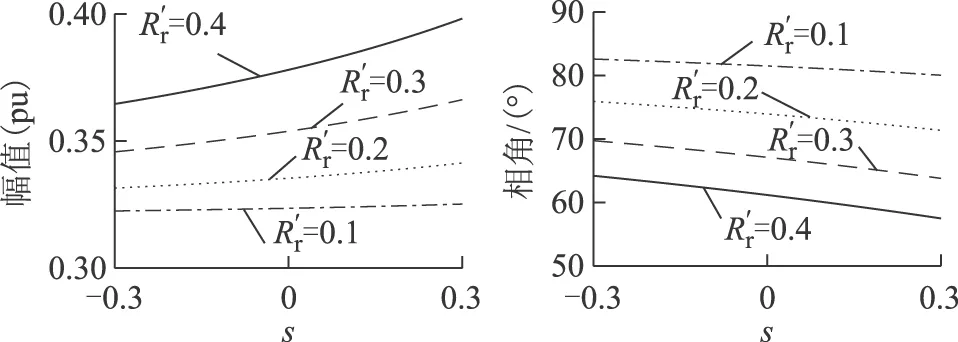
图6 Zw-的幅值相角特征Fig.6 Amplitude and angle characteristics ofZw-

通过Zw+与Zw-的对比，可以得出以下结论：

1)Zw+的幅值通常比Zw-的幅值大，且暂态过程中Zw+的幅值波动明显，而Zw-的幅值基本稳定。

2)Zw+的相角存在一个暂态变化过程，最终稳定在-90°～-180°，而Zw-的相角在0°～90°，两者差异非常大。

DFIG等效正、负序阻抗在幅值和相角上的巨大差异将对传统基于同步发电机正、负序阻抗相等而设计的保护原理产生影响。

4 仿真实验及结果分析

利用Matlab/Simulink平台搭建如图7所示的DFIG并网仿真模型，DFIG和系统的参数分别见表1和表2。

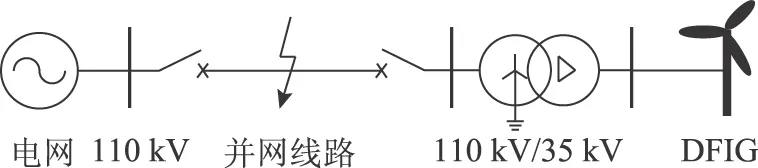
图7 DFIG并网仿真模型Fig.7 Simulation model of grid-connected DFIG

表1 DFIG参数

表2 系统参数

4.1 DFIG等效正、负序阻抗解析式的仿真验证

为了验证式(22)、式(26)DFIG等效正、负序阻抗解析表达式的正确性，图8给出了t=0.1s并网线路靠DFIG侧发生故障时序阻抗的仿真与计算结果比较。图8a为发生A相接地故障、DFIG运行转差s=-0.2、投入0.1(pu)撬棒电阻；图8b为发生BC两相接地故障、DFIG运行转差s=0.2、投入0.3(pu)撬棒电阻。由于全波傅氏算法计算的结果是一个周波前的状态，所以仿真和计算结果的比较从t=0.12 s开始。从图中看到，Zw+、Zw-的计算值与仿真值非常接近，只是在Zw+的暂态变化过程中稍有偏差，但两者变化趋势是一致的，不影响对Zw+特征的分析。以上仿真结果充分说明了DFIG等效正、负序阻抗解析表达式的有效性。

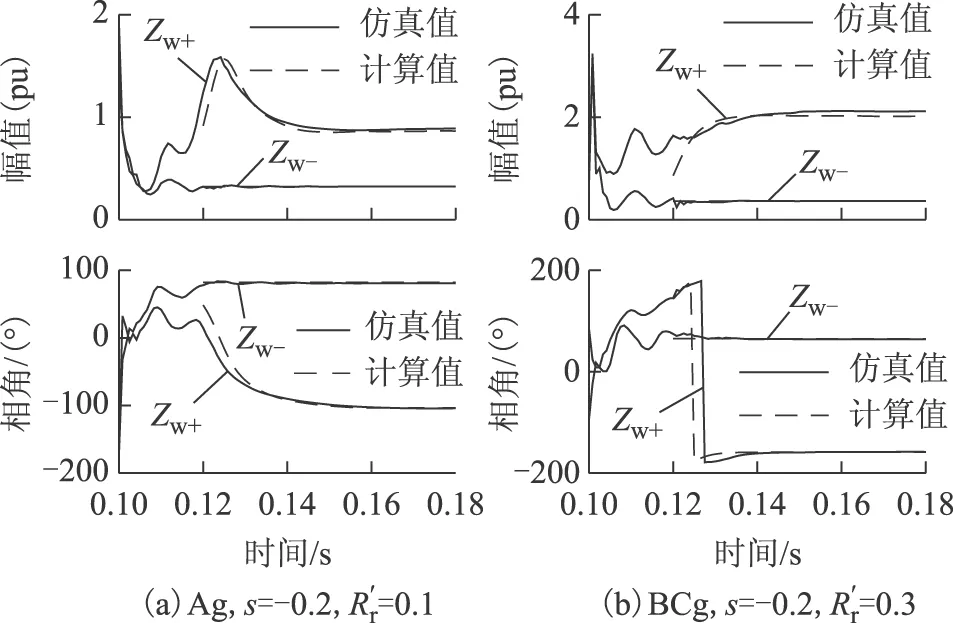
图8 等效序阻抗仿真与计算结果比较Fig.8 Comparison of simulation and calculation results for equivalent sequence impedances

4.2DFIG等效正、负序阻抗暂态变化特征仿真

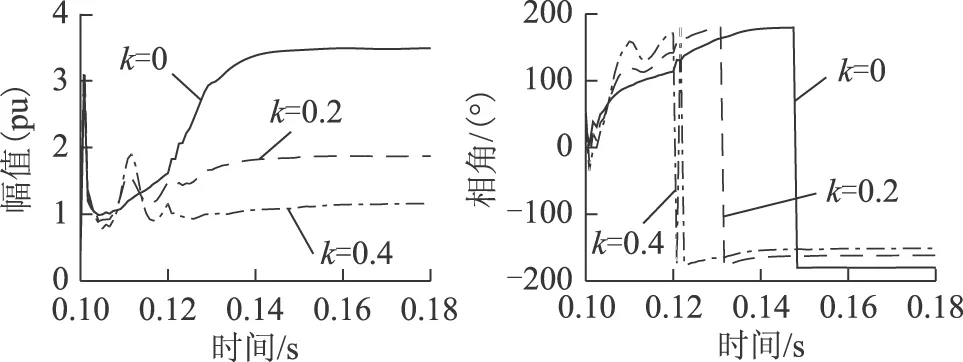
图9 工况 1下Zw+的暂态变化特征Fig.9 Transient variation characteristics ofZw+in Case 1

图10、图11分别给出了工况 2仿真下Zw+、Zw-幅值和相角的变化过程。从图10中看到，暂态过程中Zw+的幅值有明显波动，其中s≤0时波动幅度远大于s>0，主要是因为s≤0时，当Δis+变化到实轴附近时(见图3，此时Zw+的相角在0°或180°附近)，其幅值较小，使得Zw+的幅值出现较大的峰值。而Zw+的相角当s<0时逐渐减小，这是投入撬棒电阻较小的缘故，s≥0时，Zw+的相角均逐渐增大。综上可知Zw+的暂态变化特征与图3的分析结果完全吻合。暂态过程结束后，同样从图中可以看到仿真结果与图4基本相符。

图10 工况 2下Zw+的暂态变化特征Fig.10 Transient variation characteristics ofZw+in Case 2

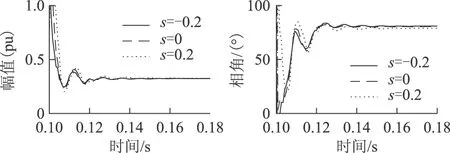
图11 工况 2下Zw-的暂态变化特征Fig.11 Transient variation characteristics ofZw-in Case 2

由图11可知，Zw-的暂态变化过程(0.12s后)并不明显，经过微小的波动后便达到了稳态，虽然s在很大范围内变化，但Zw-的幅值和相角基本保持恒定，说明Zw-受s的影响较小，验证了前述理论分析的结论。

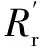
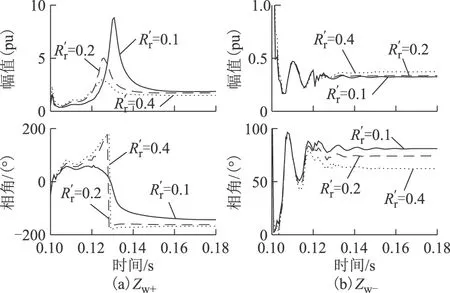
图12 Case 3下Zw+和Zw-的暂态变化特征Fig.12 Transient variation characteristics of Zw+ and Zw- in Case 3

另外，综合以上仿真结果还可以看到，Zw+的幅值一般要远大于Zw-的幅值，达稳态后，Zw+的相角在-90°～-180°，Zw-的相角在0°～90°。

5 结论

DFIG等效正、负序阻抗特征对相关继电保护原理的研究有着重要意义，虽然目前已有文献指出两者不相等，但缺乏深入全面的理论分析研究，本文考虑撬棒保护，详细研究了DFIG等效正、负序阻抗的暂态变化特征，主要创新点和结论如下：

1)给出了DFIG等效正、负序阻抗的定义；基于DFIG定子故障电流推导了DFIG等效正、负序阻抗的解析表达式。

2)从初始时刻、暂态变化过程、稳态三个阶段分析了DFIG等效正、负序阻抗幅值和相角的特征，尤其是暂态变化特征。

3)通过理论分析和仿真验证得出：DFIG等效正序阻抗存在一个明显的暂态变化过程，其幅值较大且有波动，相角从初相角逐渐增大或减小，并最终稳定在-90°～-180°；等效负序阻抗暂态变化过程不明显，其幅值较小，相角在0°～90°。

DFIG等效正、负序阻抗的暂态变化过程与传统同步发电机差异很大，将对基于同步发电机序阻抗特征而设计的继电保护原理造成影响。

附 录

衰减转速频率分量对傅氏算法的影响：

为便于数学推导，采用连续傅里叶变换代替离散傅里叶变换进行分析。设衰减转速频率分量i(t)为

(A1)

式中，A为幅值；φ为初相角；ωs=100π。

由全波基频傅氏算法的实、虚部计算公式得

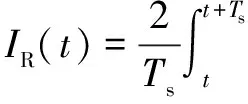
(A2)

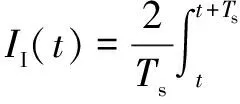
(A3)

式中，Ts为基频周期。

将式(A1)代入经过积分运算可得

(A4)

(A5)

其中

(A6)

(A7)

将s换成s-2即为X(s-2)、Y(s-2)。

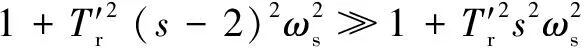
(A8)

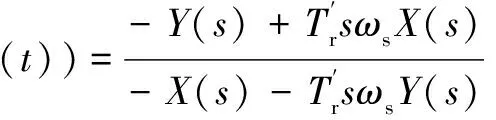
(A9)

对比式(A1)、式(A8)可知，衰减转速分量经过傅氏算法后幅值仍然按照相同的指数规律衰减，只是相差一个系数ΔA，其表达式为

(A10)

由式(A9)知，衰减转速分量经过基频傅氏算法后的相角将以频率-sωs变化，且初相角不再是φ，变化了Δφ=φ(0)-φ，Δφ可通过式(A11)计算。

(A11)

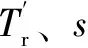
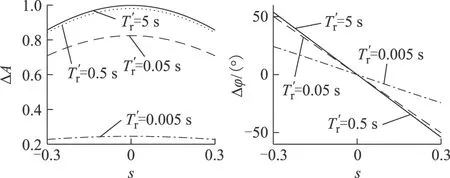
附图1 ΔA与Δφ随、s的变化关系App.Fig.1 The relationship ofΔAandΔφvaried ands

如果采用半波傅氏算法，只需将Ts换成Ts/2，以上结论仍成立。

[1] 王晨清，宋国兵，迟永宁，等.风电系统故障特征分析[J].电力系统自动化，2015，39(21)：52-58.WangChenqing，SongGuobing，ChiYongning，etal.Faultcharacteristicsanalysisofwindpowersystem[J].AutomationofElectricPowerSystems，2015，39(21)：52-58.

[2] 欧阳金鑫，熊小伏，张涵轶.电网短路时并网双馈风电机组的特性研究[J].中国电机工程学报，2011，31(22)：17-25.OuyangJinxin，XiongXiaofu，ZhangHanyi.CharacteristicofDFIG-basedwindgenerationundergridshortcircuit[J].ProceedingsoftheCSEE，2011，31(22)：17-25.

[3] 焦在强.大规模风电接入的继电保护问题综述[J].电网技术，2012，36(7)：195-201.JiaoZaiqiang.Asurveyonrelayprotectionforgrid-connectionoflarge-scalewindfarm[J].PowerSystemTechnology，2012，36(7)：195-201.

[4] 肖繁，张哲，尹项根，等.含双馈风电机组的电力系统故障计算方法研究[J].电工技术学报，2016，31(1)：14-23.XiaoFan，ZhangZhe，YinXianggen，etal.Thefaultcalculationmethodofpowersystemsincludingdoubly-fedinductiongenerators[J].TransactionsofChinaElectrotechnicalSociety，2016，31(1)：14-23.

[5] 尹俊，毕天姝，薛安成，等.计及低电压穿越控制的双馈风力发电机组短路电流特性与故障分析方法研究[J].电工技术学报，2015，30(23)：116-125.YinJun，BiTianshu，XueAncheng，etal.Studyonshortcircuitcurrentandfaultanalysismethodofdoublefedinductiongeneratorwithlowvoltageride-throughcontrolstrategy[J].TransactionsofChinaElectrotechnicalSociety，2015，30(23)：116-125.

[6] 撖奥洋，张哲，尹项根，等.双馈风力发电系统故障特性及保护方案构建[J].电工技术学报，2012，27(4)：233-239.HanAoyang，ZhangZhe，YinXianggen，etal.Researchonfaultcharacteristicandgridconnecting-pointprotectionschemeforwindpowergenerationwithdoubly-fedinductiongenerator[J].TransactionsofChinaElectrotechnicalSociety，2012，27(4)：233-239.

[7] 张保会，李光辉，王进，等.风电接入电力系统故障电流的影响因素分析及对继电保护的影响[J].电力自动化设备，2012，32(2)：1-8.ZhangBaohui，LiGuanghui，WangJin，etal.Affectingfactorsofgrid-connectedwindpoweronfaultcurrentandimpactonprotectionrelay[J].ElectricPowerAutomationEquipment，2012，32(2)：1-8.

[8] 黄涛，陆于平，凌启程，等.撬棒电路对风电场侧联络线距离保护的影响及对策[J].电力系统自动化，2013，37(17)：30-36.HuangTao，LuYuping，LingQicheng，etal.Impactofcrowbaronwindfarmsideinterconnectionlinedistanceprotectionandmitigationmethod[J].AutomationofElectricPowerSystems，2013，37(17)：30-36.

[9] 熊小伏，齐晓光，欧阳金鑫.双馈风电机组短路电流对变压器保护二次谐波制动的影响[J].中国电机工程学报，2014，34(13)：2201-2209.XiongXiaofu，QiXiaoguang，OuyangJinxin.Effectofdoubly-fedwindturbinesshort-circuitcurrentonsecondharmonicescapementoftransformerprotection[J].ProceedingsoftheCSEE，2014，34(13)：2201-2209.

[10]裘愉涛，陈水耀，杨恢宏，等.交直流混联系统突变量方向元件适用性研究[J].电力系统保护与控制，2012，40(13)：115-120.QiuYutao，ChenShuiyao，YangHuihong，etal.Researchonapplicabilityofdirectionalelementbasedonthepower-frequencyvariationinAC-DChybridsystem[J].PowerSystemProtectionandControl，2012，40(13)：115-120.

[11]王晨清，宋国兵，刘凯，等.突变量保护对风电接入系统的适应性分析[J].中国电机工程学报，2014，34(31)：5485-5492.WangChenqing，SongGuobing，LiuKai，etal.Adaptabilityanalysisoffaultcomponentprotectionofpowersystemswithwindfarms[J].ProceedingsoftheCSEE，2014，34(31)：5485-5492.

[12]HuangTao，LuYuping.Improvedsuperimposedcurrentphaseselectorofwindfarmwithcrowbarsystem[C]//IEEEPESGeneralMeeting，NationalHarbor，MD，USA，2014：1-5.

[13]沈枢，张沛超，方陈，等.双馈风电场故障序阻抗特征及对选相元件的影响[J].电力系统自动化，2014，38(15)：87-92.ShenShu，ZhangPeichao，FangChen，etal.CharacteristicsofsequenceimpedanceofDFIGplantandinfluenceonphaseselector[J].AutomationofElectricPowerSystems，2014，38(15)：87-92.

[14]黄涛，陆于平.投撬棒后双馈风机暂态电势的变化特性分析[J].电网技术，2014，38(10)：2759-2765.HuangTao，LuYuping.AnalysisontransientEMFvariationcharacteristicofdoublyfedinductiongeneratoraftercrowbarprotectionactivated[J].PowerSystemTechnology，2014，38(10)：2759-2765.

[15]王振树，刘岩，雷鸣，等.基于Crowbar的双馈机组风电场等值模型与并网仿真分析[J].电工技术学报，2015，30(4)：44-51.WangZhenshu，LiuYan，LeiMing，etal.Doubly-fedinductiongeneratorwindfarmaggregatedmodelbasedoncrowbarandintegrationsimulationanalysis[J].TransactionsofChinaElectrotechnicalSociety，2015，30(4)：44-51.

[16]XiaoShuai，YangGeng，ZhouHonglin，etal.AnLVRTcontrolstrategybasedonfluxlinkagetrackingforDFIG-basedWECS[J].IEEETransactionsonIndustrialElectronics，2013，60(7)：2820-2832.

[17]张迪，魏艳君，马利轩，等.不平衡电网电压下基于滑模变结构控制双馈风电系统网测变流器控制策略[J].电工技术学报，2015，30(10)：266-275.ZhangDi，WeiYanjun，MaLixuan，etal.Sliding-modecontrolforgrid-sideconvertersofDFIG-basedwindpowergenerationsystemunderunbalancedgridvoltageconditions[J].TransactionsofChinaElectrotechnicalSociety，2015，30(10)：266-275.

[18]张保会，王进，原博，等.风电接入对继电保护的影响(四)——风电场送出线路保护性能分析[J].电力自动化设备，2013，33(4)：1-5.ZhangBaohui，WangJin，YuanBo，etal.Impactofwindfarmintegrationonrelayprotection(4)：performanceanalysisforwindfarmoutgoingtransmissionlineprotection[J].ElectricPowerAutomationEquipment，2013，33(4)：1-5.

[19]欧阳金鑫.变速恒频风电机组并网故障机理与分析模型研究[D].重庆：重庆大学，2012.

[20]孔祥平，张哲，尹项根，等.计及励磁调节特性影响的双馈风力发电机组故障电流特性[J].电工技术学报，2014，29(4)：256-265.KongXiangping，ZhangZhe，YinXianggen，etal.FaultcurrentcharacteristicsofDFIGconsideringexcitationandregulationcharacteristics[J].TransactionsofChinaElectrotechnicalSociety，2014，29(4)：256-265.

[21]Lok-FuP，DinavahiV.Real-timesimulationofawindenergysystembasedonthedoubly-fedinductiongenerator[J].IEEETransactionsonPowerSystems，2009，24(3)：1301-1309.

(编辑 赫蕾)

Study on Equivalent Sequence Impedances of DFIG with Crowbar Protection

HuangTao1LuYuping1WangYe2

(1.School of Electrical Engineering Southeast University Nanjing 210096 China 2.Jiangsu Electric Power Company Nanjing 210024 China)

The characteristics of doubly fed induction generator(DFIG)equivalent sequence impedances(ESIs)have a huge impact on fault component based relay protections.To provide theoretical basis for DFIG ESIs and related transient studies，the definition of DFIG ESIs is first given.Analytical equations of DFIG ESIs under activated crowbar protection are derived based on stator fault sequence currents.Characteristics and significant factors of DFIG ESIs are studied in detail.It is observed that equivalent positive sequence impedance has an evident transient change process while equivalent negative sequence impedance doesn′t.The amplitude of the former is larger and fluctuant while the latter is smaller，and the steady phase angle of the former is between -90° and -180° while the latter is between 0°and 90°.Finally，the theoretical analysis are verified by simulation experiments.

Doubly fed induction generator，crowbar protection，equivalent sequence impedances，amplitude and angle，transient variation characteristic

国家自然科学基金资助项目(51377022，51677026)。

2016-04-06 改稿日期2016-11-30

TM77

黄 涛 男，1988年生，博士研究生，研究方向为电力系统继电保护及风力发电保护与控制。

E-mail：taoh545@126.com(通信作者)

陆于平 男，1962年生，教授，博士生导师，研究方向为电力系统继电保护及分布式发电系统保护与控制。

E-mail：luyuping@seu.edu.cn