计及主动配电网转供能力的可再生电源双层优化规划

刘 佳 徐 谦 程浩忠 兰 洲 田 园

(1.上海交通大学电力传输与功率变换控制教育部重点实验室 上海 200240 2.国网浙江省电力公司经济技术研究院 杭州 310008)



计及主动配电网转供能力的可再生电源双层优化规划

刘 佳1徐 谦2程浩忠1兰 洲2田 园1

(1.上海交通大学电力传输与功率变换控制教育部重点实验室 上海 200240 2.国网浙江省电力公司经济技术研究院 杭州 310008)

在主动管理(AM)模式下，提出了一种考虑主动配电网转供能力的可再生电源(RES)优化配置模型。以年综合费最小为上层目标，每个场景的配电网运行费最小为下层目标，该模型计及了系统故障负荷的转供和包括RES出力切除、RES功率因数调整、有载调压变压器分接头调节和需求侧管理在内的4种AM措施。考虑RES出力随机性及负荷波动性，利用准蒙特卡罗模拟和奇异值分解生成风、光荷相关性样本矩阵并采用模糊C-means聚类对场景进行缩减。应用动态小生境差分进化与原对偶内点算法相联合的策略对模型加以求解。通过算例对比是否考虑AM措施和转供能力下的三种情境仿真结果验证了模型和方法的有效。

主动配电网 可再生电源 双层优化规划 主动管理 转供能力

0 引言

近年来，作为发、输电系统和终端用户间的重要环节，配电网层面正大量接入以风电和光伏为代表的可再生电源(Renewable Energy Sources，RES)，经历了从无源电网到有源电网的转变。由于双向潮流的出现，大大增加了配电网的不确定性和复杂性，给系统优化规划及运行带来了巨大的挑战[1]。为了充分发挥RES在降低网损、改善线路潮流等方面的积极作用，需对其进行优化规划。

在传统的被动管理模式下，RES接入配电网后遵循“安装即忘记”的原则，这样不仅无法充分发挥RES的优势，而且在一定程度上限制了RES的接入。随着配电自动化和配电管理技术在中压配电网中的广泛应用，馈线所带负荷信息可通过馈线终端装置快速获得[2]，远程开关控制也将变得更加迅速[3]，使得配电网具有了可随外部环境的变化实现负荷转供和故障恢复的能力[4，5]及主动性特征[6]。主动配电网(Active Distribution Network，ADN)成为了配电网发展的一种新模式。一方面可对接入配电网的RES和其他设备进行主动管理(Active Management，AM)；另一方面可提高系统应对N-1故障能力和实现负荷有效转移。ADN的出现对RES规划问题提出了新的要求。

为提高ADN中的RES渗透容量，充分发挥ADN的资产效率，文献[6-11]对AM模式下的RES规划进行了相关研究。文献[6]构造了一种计及可靠性成本、网络损耗、购电费、网架投资成本在内的总费用最小的RES和ADN协调优化规划模型。文献[7]提出了一种通过识别ADN中薄弱节点的RES优先优化配置模型。文献[8]考虑时变负荷和能源单价浮动，建立了计及RES接入后优化运行问题的长期RES动态规划模型。文献[9]以RES渗透容量最大为目标建立优化模型，并利用多时段的最优潮流算法对其加以求解。文献[10]提出了一种AM模式下的分布式风电源双层选址定容规划模型，并将所得RES优化规划方案与传统机会约束规划模型所得RES配置方法进行对比。文献[11] 建立了一种间歇式分布式电源在ADN当中的机会约束优化规划模型，并给出了结合蒙特卡罗模拟、遗传算法和前推回代法的求解方法。

上述文献是从不同角度出发，建立了N安全下的RES选址定容规划模型并采用优化算法加以求解。但由于配电网中某个元件(如主变压器、馈线等)故障也属于不确定性范畴，而现有模型仅包含了负荷波动、间歇性RES出力等正常工况下的不确定因素，不确定性的内涵亟待完善。现有模型均未能充分计及ADN具有比传统配电网更灵活的N-1后转供能力，所得RES规划方案也未必满足相关要求。上述研究也未能对RES接入后的系统N-1转供安全性给出定量评估。因此，有必要在RES优化配置阶段就考虑ADN故障后转供能力。

为弥补现有RES规划方法的不足，本文建立了计及AM措施和ADN转供能力的RES双层优化配置模型。利用模糊C-means聚类法对采用准蒙特卡罗模拟(Quasi Monte Carlo Simulation，QMCS)和奇异值分解(Singular Value Decomposition，SVD)生成的风、光荷相关性样本矩阵进行场景约简。采用动态小生境差分进化算法(Dynamic Niche Differential Evolution Algorithm，DNDEA)联合原对偶内点算法(Primal-Dual Interior Point Method，PDIPM)的混合方法求解规划模型。最后，算例仿真结果表明文中模型所得RES优化配置方案提高了系统应对N-1故障的能力。

1 不确定因素建模

1.1 RES出力概率模型

风速通常采用双参数Weibull分布来描述[12]。

(1)

式中，V为风电叶轮轮毂处的风速；r和c分别为形状参数和尺度参数。

风电出力SWTG与风速V之间的关系可近似用分段函数[12]表示为

(2)

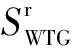
光照强度通常采用Beta分布[13]描述为

(3)

式中，I和Imax分别为光照强度及其最大值；α和β为Beta分布的两个参数；Γ(·)为伽玛函数。

光伏出力SPVG与光照强度I之间的关系可近似表示为[13]

(4)

1.2 负荷不确定性模型

负荷采用正态分布的概率模型来描述[13]。

(5)

式中，SL、μp和σp分别为负荷的随机量、期望和标准差。

1.3 配电网安全距离模型

配电网安全距离(DistributionSystemSecurityDistance，DSSD)是定量评估配电网N-1转供安全裕度的一种新方法，它建立在配电网安全域理论上[14，15]。配电网安全域ΩDSSR是指在馈线N-1和主变压器N-1转供约束下，配电网能够安全运行的所有工作点的集合[14]，因此，工作点在配电网安全域中的位置可以反映系统N-1转供安全性，并利用其到配电网安全域各边界的欧氏距离，即DSSD，来量化反映这一数据。基于交流潮流的DSSD模型可表述为

(6)

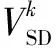
上述模型的具体计算方法已在文献[15]中定义，在此不再赘述。当某工作点的安全距离为负值时，说明其不满足N-1安全转供，且安全距离越小，表征转供不安全程度越高；当某工作点的安全距离为正值时，说明其满足N-1安全转供，且安全距离越大，表征转供安全程度越高[14]。

2 相关样本数据生成及简化

2.1 QMCS和SVD生成相关性样本

对于含风速、光照强度和负荷的3维随机变量X=[X1,X2,X3]T，设其相关系数矩阵为[ρij]3×3，其中相关系数ρij定义为

(7)

式中，σi和σj分别为Xi和Xj的标准差；cov(Xi,Xj)为变量Xi、Xj的协方差。

本文采用基于Sobol序列的QMCS进行样本采样[16]。同时，考虑到相关系数矩阵非正定或非满秩，其Cholesky分解不存在，而由于相关系数矩阵均为对称阵，其SVD一直存在，因此，本文采用SVD对相关系数矩阵进行处理。QMCS联合SVD能够生成基于目标风、光荷相关系数矩阵[ρobj]3×3的相关样本矩阵的理论依据可详见文献[17]。

应用QMCS和SVD产生相关性RES出力矩阵的具体过程如下:

1)设采样规模为N，利用QMCS对风速、光照强度和负荷3个随机输入变量进行采样，得到一个3×N阶的初始样本矩阵S0。

2)随机生成一个3×N阶的顺序矩阵L，并按照式(7)计算L的相关系数矩阵ρL。

3)按照式(8)对ρL进行SVD并通过式(9)来消除由于随机排列而产生的相关性。

(8)

(9)

式中，UL为酉矩阵；ΣL为由矩阵奇异值构成的对角矩阵。

4)按照式(10)对目标相关系数矩阵[ρobj]3×3进行SVD，并通过式(11)令Zu的相关系数矩阵与[ρobj]3×3近似相等。

(10)

(11)

5)更新初始样本矩阵S0中的元素得到新的样本矩阵Su。

2.2 模糊C-means聚类法简化样本数

为降低计算量和减少计算耗时，本文先采用模糊C-means聚类算法对2.1节得到的样本矩阵Su进行约简，从而减少计算最优潮流的次数而提高计算效率。模糊C-means聚类法[18，19]的核心求解思路是：从任意一个聚类中心开始，搜索目标函数值最小的点，并不断更新聚类中心和调整样本模糊隶属度，最终确定样本所属大类。该方法对样本数据的聚类中心及隶属度的求取公式为

(12)

(13)

式中，xp为第p个样本；μq为第q个聚类中心；δpq为xp属于μq的隶属度；ε为模糊度；Y为聚类数；N为样本数。

统计落入每个类别的样本数Ny(y=1,2,…,Y)，并计算每个场景发生的频率py。

(14)

由大数定律可知，在满足样本数N足够大的前提下，各场景发生的概率等于频率py。

3 RES双层优化配置模型

本文采用场景构建法将不确定因素(RES出力和负荷波动)对电网运行的作用效果转换为一系列确定的场景进行处理。考虑有载调压变压器(On-LoadTapChanger，OLTC)抽头调整、RES出力切除、RES功率因数调节以及需求侧管理4种AM措施和N-1转供约束，本文建立的RES优化配置模型在优化RES配置方案的同时，亦需优化ADN在每个场景下的运行方式，属于典型的双层规划问题[20]。上层是以年综合费最小为目标的RES优化配置问题，下层则是以每个场景的ADN运行费最小为目标的优化运行问题。上层规划将RES配置方案传递给下层，下层规划则在此基础上对每个场景下的ADN进行优化运行模拟，并将计算结果传递给上层，从而指导上层规划的决策。

3.1 上层规划模型

具体数学表达式如下：

1)目标函数。

(15)

式中，CSUM、CI、COM,s、CAM,s、CP,s、CCE,s和CDSM,s分别为年综合费、RES投资费、RES年运行维护费、RES年AM费、配电网向上级电网年购电费、碳排放成本和需求侧管理成本；Ns为总场景数；下标中包含“s”的变量均表示场景s的值。

2)约束条件。

RES安装容量上限约束为

(16)

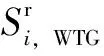
RES安装容量离散性约束为

(17)

(18)

3.2 下层规划模型

具体数学表达式如下：

1)目标函数。

minCOM,s+CAM,s+CP,s+CCE,s+CDSM,s

(19)

2)约束条件。

潮流方程约束为

(20)

(21)

式中，PGi,s和QGi,s分别为节点i发出的有功以及无功功率；PLi,s和QLi,s分别为节点i的有功以及无功需求；Ui,s和Uj,s分别为节点i和节点j的电压；Gij为支路电导；Bij为支路电纳；θij,s为节点i和节点j的电压相角差；Nbus为配电网的节点数。

ADN转供约束为

(22)

节点电压约束为

(23)

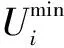
OLTC二次侧电压上、下限约束为

(24)

RES出力上、下限约束为

(25)

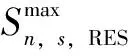
RES功率因数角上、下限约束为

(26)

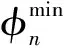
负荷中断量上、下限约束为

(27)

CI、COM,s、CAM,s、CP,s、CCE,s和CDSM,s为

(28)

(29)

(30)

CP,s=psρSgrid,s,PT

(31)

CCE,s=psηλSgrid,s,PT

(32)

(33)

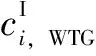
4 求解算法和步骤

分析上述RES双层优化配置模型，其是含有多个决策变量的非线性混合整数双层规划问题。本文利用DNDEA联合PDIPM的混合方法求解双层规划模型，该算法克服了差分进化算法在初期搜索速度快，后期易陷入局部最优点的缺点。

4.1DNDEA

差分进化算法(DifferentialEvolutionAlgorithm，DEA)[20]的基本过程可参见文献[21]，这里不再赘述。本文综合运用两轮联赛选择，两点交叉，单点均匀变异，交叉以及变异均采用不等概率，并引入精英保留策略。

与大多数群体智能算法一样，DEA也存在容易陷入局部最优和收敛性较差等缺点。为了增加DEA对问题解空间的搜索性能，引入动态小生境机制[22，23]，得到DNDEA。动态小生境机制可促使群体内个体间协同合作，保持解的多样性，提高全局搜索能力，使算法易于找出优化问题的所有局部最优解和全局最优解，适合多峰函数的优化[23]。

4.2 求解步骤

基于DNDEA联合PDIPM的混合策略求解RES双层优化配置模型的具体流程如图1所示。

图1 DNDEA联合PDIPM求解优化模型流程Fig.1 Flow chart of solving optimal model based on DNDEA and PDIPM

5 算例分析

5.1 算例基本情况

算例配电网网架结构如图2所示。算例共有3座33kV变电站、6台主变压器，20条11kV馈线和104个已有负荷节点，各节点负荷类型均相同且功率因数为0.85。算例中，各主变压器及线路数据和已有负荷均值数据分别见表1和表2。负荷的标准差为均值的10%。

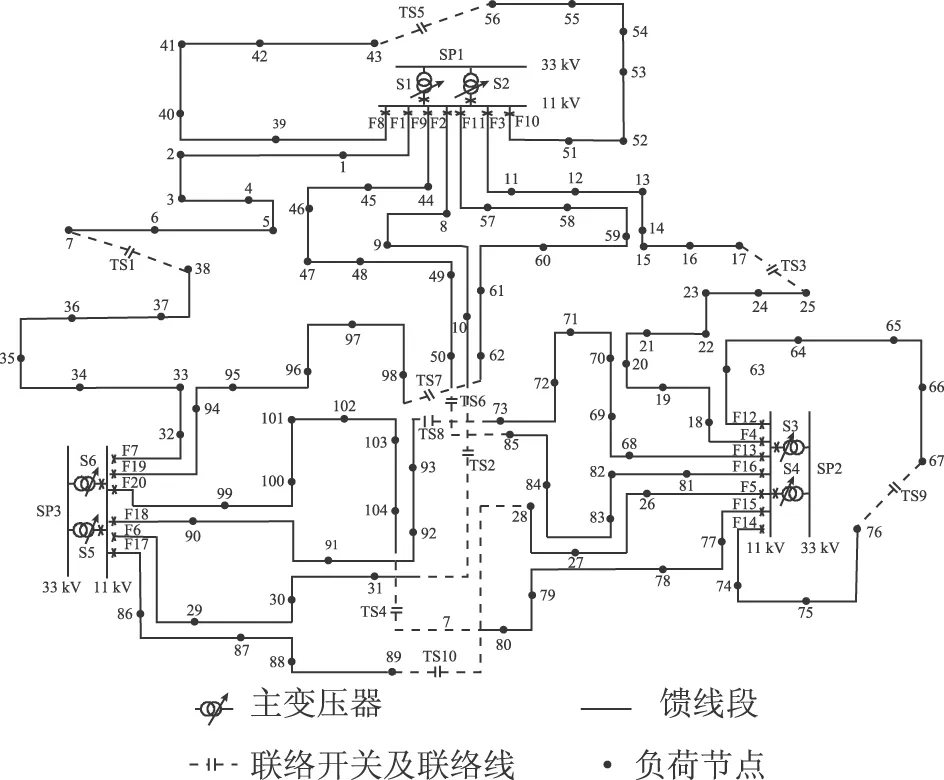
注：F1表示第1条馈线，以此类推。图2 算例网络Fig.2 Test system

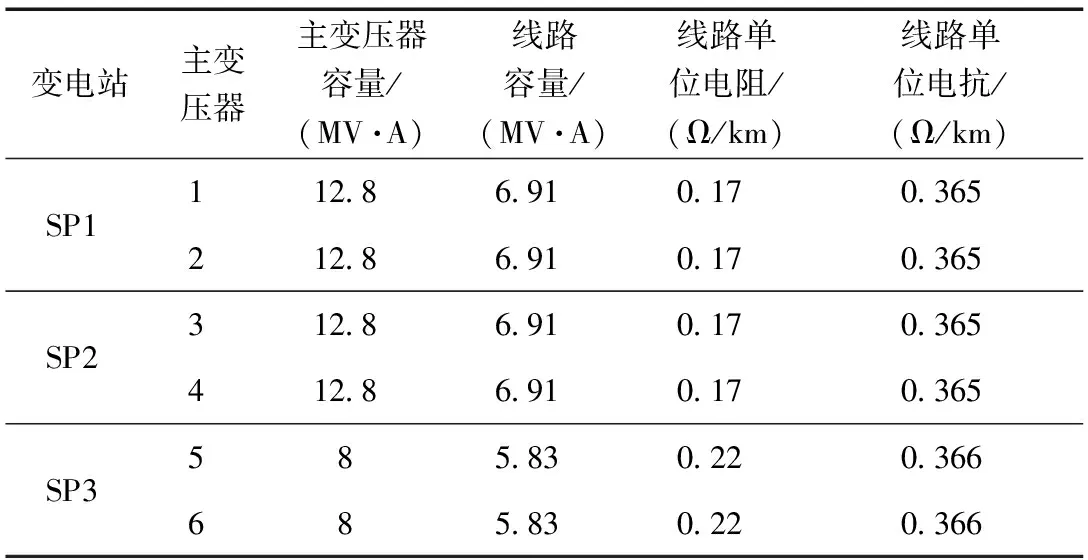
表1 各主变压器及线路数据

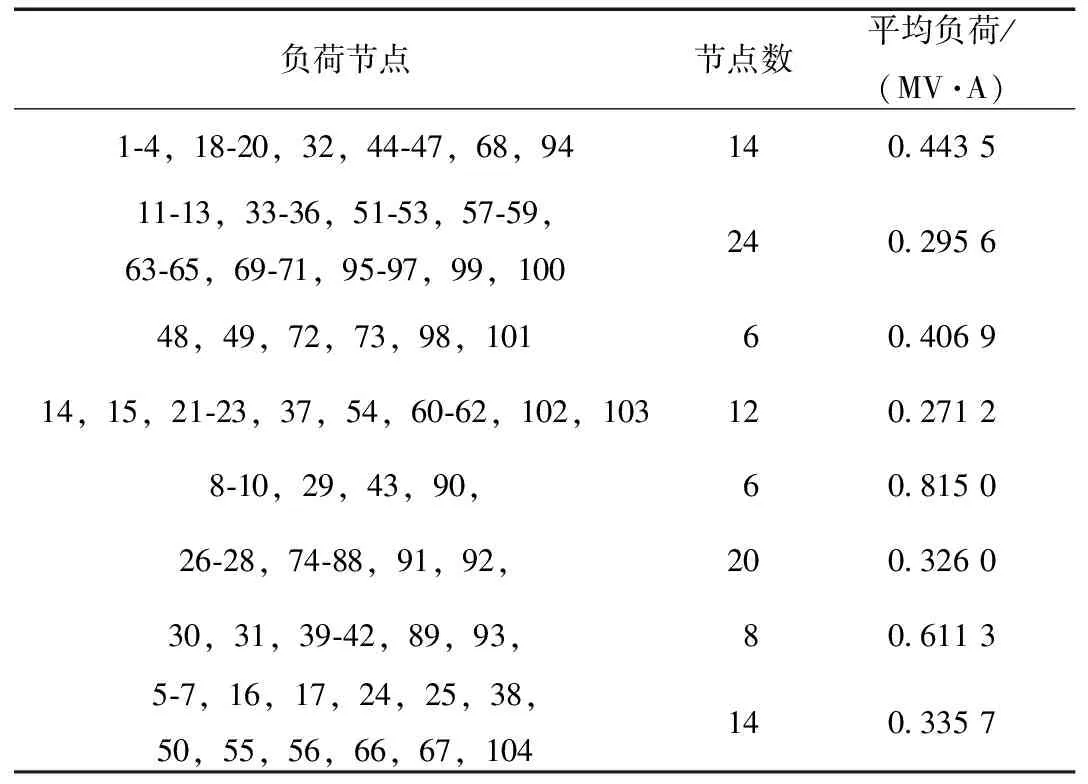
表2 已有负荷均值数据

一些规划参数如下：RES的待选安装节点为3、5、7、10、40、42、47和49，每个待选安装节点的RES容量上限为5 MW，可中断负荷点为4、6、9、41、43、46、48和50，中断负荷恒功率因数被中断。单台风电的额定容量为0.5 MW，切入风速、额定风速和切出风速分别为3 m/s、13 m/s、20 m/s；风电的单位容量投资费为150 万美元/MW，单位发电量的运行维护费和AM费分别为30美元/(MW·h)和22.5 美元/(MW·h)；风速服从r=2.15和c=8.32的Weibull分布。单个光伏的额定容量为0.5MW，额定光照强度为0.5kW/m2，最大光照强度为0.6kW/m2；光伏的单位容量投资费为175 万美元/MW，单位发电量的运行维护费和AM费分别为40美元/(MW·h)和30 美元/(MW·h)；光照强度服从α=0.55和β=1.38的Beta分布。风电和光伏的使用年限均为20年，贴现率为0.06。节点电压范围为0.95(pu)～1.05(pu)。上级电网碳排放强度为639.2kg/(MW·h)，单位碳排放成本为10 美元/t，可中断负荷点的补偿单价为350 美元/(MW·h)。DNDEA的参数为：种群规模为50，最大迭代次数为50，交叉率和缩放因子均从0.9线性递减到0.1。模糊C-means聚类数为50。

AM措施调节范围参数如下：有载调压变压器二次侧电压的调节范围为0.95(pu)～1.05(pu)，RES出力的削减率调节范围为0～50%，RES的功率因数调节范围为+0.98～-0.98，可中断负荷点的中断量范围为0～全部。

本文分别选用年综合费、安全距离变异系数作为评估RES配置方案经济性、安全性的指标，权重系数均设为0.5。本文所有仿真的计算条件是：计算机CPU为i7-3 820，主频为3.6GHz，内存为8GB，在Matlab2013a平台上编制计算程序。

5.2 基于采样数据的选址定容规划结果

基于采样数据，将本文所提出的模型用于算例研究，并采用DNDEA联合PDIPM对规划模型进行求解，得到考虑AM措施和ADN转供能力的RES优化配置方案(记为方式1)见表3。作为对比，分别将规划前、仅考虑ADN转供能力(记为方式2)和仅考虑AM措施(记为方式3)的RES规划方案和相应的各部分费用、RES渗透容量同样列于表3当中，可以看出，是否考虑AM措施和ADN转供能力将会改变RES的优化配置方案，从而影响规划方案的经济性以及RES渗透率。

此外，由表3还可以看出，同一方式下，各RES安装节点配置的风电和光伏数量也不尽相同。这主要是因为系统各节点负荷功率、风电和光伏输出功率在时空范围内的概率分布存在差异性和互补性，能让ADN在满足安全运行的同时，尽可能多地接纳RES，从而减少传统电源的供电量，实现经济效益和环境效益的综合优化。

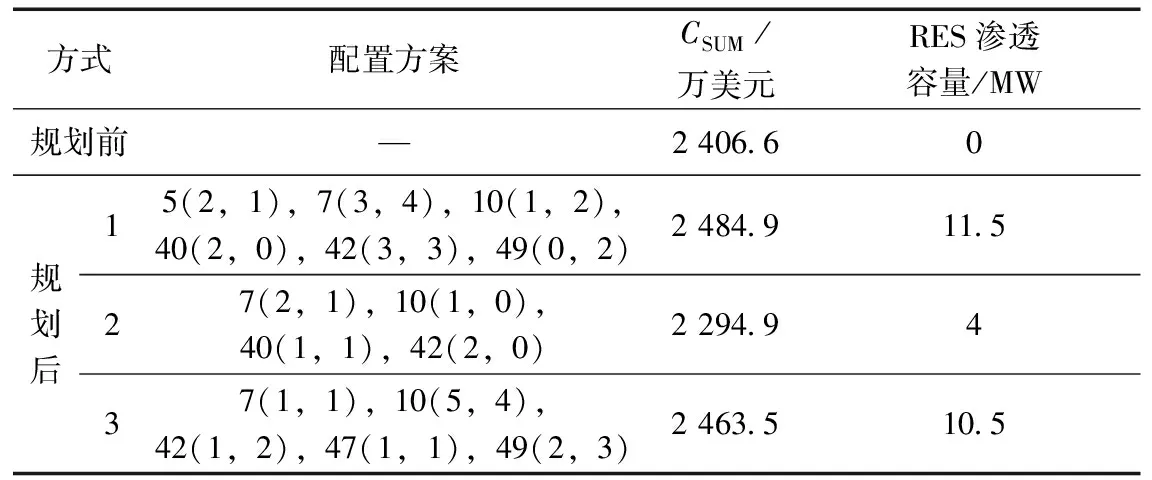
表3 不同方式下基于采样数据的规划结果

注：5(2，1)表示节点5安装2台风电，1个光伏，以此类推。

各方式所对应的各部分费用和ADN中各馈线的安全距离情况分别如图3和图4所示。

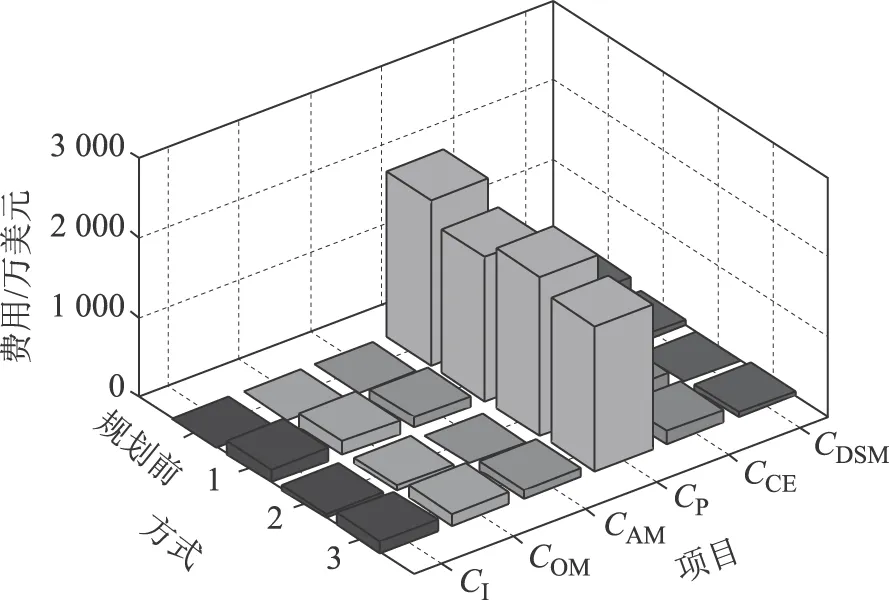
图3 不同方式下基于采样数据的各部分费用Fig.3 Costs under various modes based on sampling data

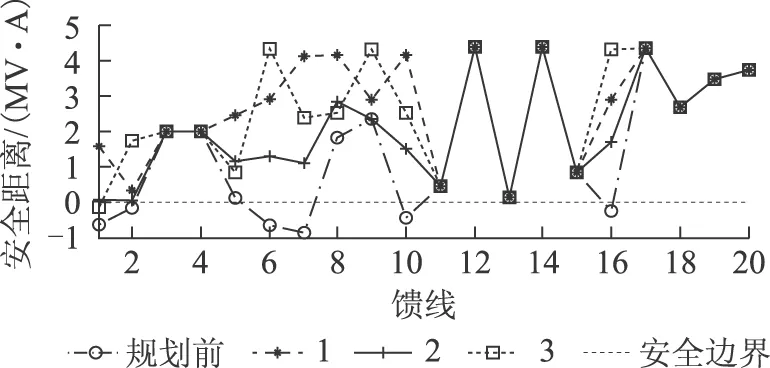
图4 各馈线基于采样数据的安全距离Fig.4 Security distance of feeders based on sampling data

由表3和图4可以看出，从综合提高系统经济性和安全性的角度出发，方式1下的RES规划方案较规划前更优。解释其原因如下：虽然方式1比规划前的年综合费用增加了78.3 万美元，增幅达3.2%，但是，考虑到规划前ADN中有6条馈线的安全距离均为负值且各条馈线的安全距离变异系数为1.25，而经方式1规划后ADN中各条馈线的安全距离均为正值且各条馈线的安全距离变异系数为0.53，相较之下，方式1比规划前的各条馈线的安全距离变异系数小了0.72，降幅达57.6%，兼顾系统经济性和安全性，方式1更好。

5.3 计及AM对规划结果的影响

为了说明AM对规划结果的影响，将方式1和方式2的规划结果进行对比分析。由表3可以看出，方式1的RES渗透容量为11.5 MW，而方式2的RES渗透容量仅为4 MW，说明AM措施可以增加RES的渗透容量，提高配电网的资产利用率。由图3可以看出，方式1的碳排放成本和年购电费分别为162.81万美元和1 797.90万美元，而方式2的碳排放成本和年购电费分别为181.62万美元和2 005.70万美元，说明AM措施可减少传统电源的发电量，达到减少碳排放的效果。

同时，由表3和图4可以看出，从综合提高系统经济性和安全性的角度出发，方式1较方式2下的RES规划方案更优。解释其原因如下：虽然方式1比方式2的年综合费用增加了190 万美元，增幅达7.6%，但是，考虑到方式2的ADN中各条馈线的安全距离变异系数为0.72，而经方式1规划后ADN中各条馈线的安全距离变异系数为0.53，相较之下，方式1比方式2的各条馈线的安全距离变异系数小了0.19，降幅达26.4%，兼顾系统经济性和安全性，方式1更好。

5.4 计及ADN转供能力对规划结果的影响

为了研究计及ADN转供能力对规划结果的影响，将方式1和方式3的规划结果进行对比分析。由表3和图4可以看出，从综合提高系统经济性和安全性的角度出发，方式1较方式3下的RES规划方案更优。解释其原因如下：虽然方式1比方式3的年综合费用增加了21.4 万美元，增幅达0.9%，但是，考虑到方式3的ADN中有1条馈线的安全距离为负值且各条馈线的安全距离变异系数为0.61，而经方式1规划后ADN中各条馈线的安全距离均为正值且各条馈线的安全距离变异系数为0.53，相较之下，方式1比方式3的各条馈线的安全距离变异系数小了0.08，降幅达13.1%，兼顾系统经济性和安全性，方式1更好。

5.5 基于历史观测数据的规划结果

为进一步论证规划模型的有效性，基于风、光荷历史观测数据进行RES规划。设该ADN所在区域的风速、光照强度和负荷的年变化曲线如图5所示。其中，风速和光照强度的曲线是基于月平均气象数据，借助HOMER软件离散得到。离散后的全年气象数据基本能够反映该区域的天气特征。利用模糊C-means方法对图5中的时序风速、光照强度和负荷数据进行聚类。在此基础上，用提出的混合求解策略对规划模型进行求解，得到不同方式下的规划结果见表4。图6给出了各馈线的安全距离情况。

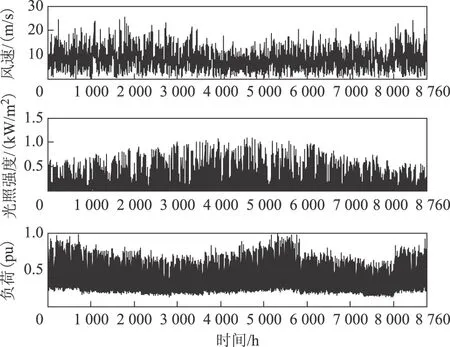
图5 风速、光照强度和负荷的年变化曲线Fig.5 Annual wind speed，illumination intensity and load curve

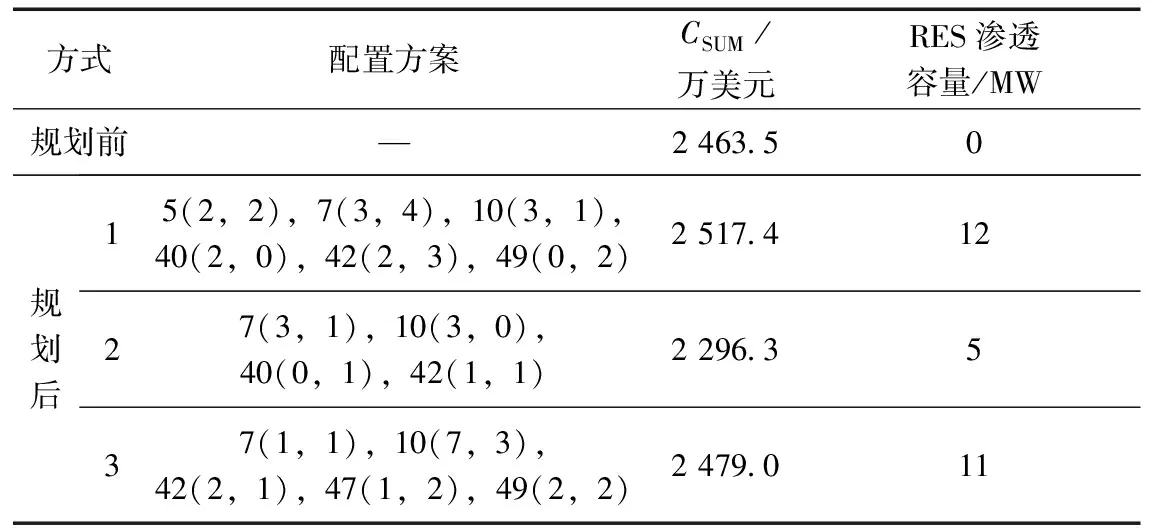
表4 不同方式下基于历史观测数据的规划结果

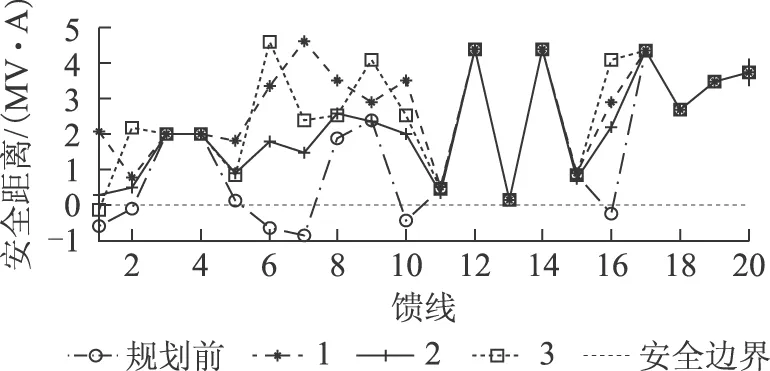
图6 各馈线基于历史观测数据的安全距离Fig.6 Security distance of feeders based on historic data

由表3和表4可以看出，各方式下基于采样数据和历史观测数据的RES优化配置方案均不相同。这主要是因为风、光荷在时空范围内的概率分布存在差异性和互补性。

由表4和图6可以看出，从综合提高系统经济性和安全性的角度出发，对比规划前和方式1、2、3下的RES规划方案，方式1最优。具体其原因可类比5.2节～5.4节中相关内容说明。

5.6 基于采样数据的算法性能比较

分别采用遍历法、K-means聚类法和模糊C-means聚类法计算方式1、2和3最优配置方案对应的年综合费，得到的结果见表5。

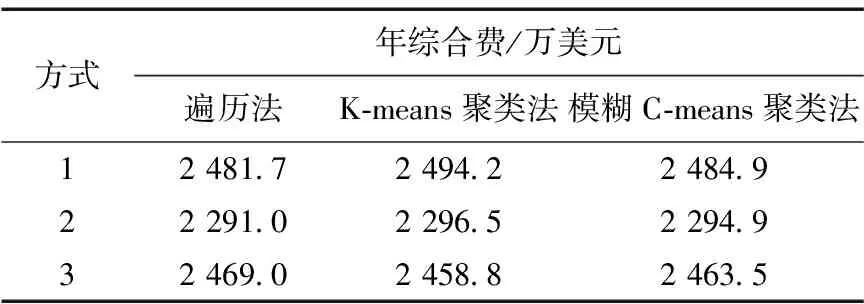
表5 三种算法性能对比

由表5中可以看出，对比K-means聚类法，运用模糊C-means聚类法约简样本所得到的计算结果与采用遍历法得到的结果更加逼近，误差更小，这表明：①运用模糊C-means聚类法对风速、光照强度和负荷样本矩阵进行简化的求解思路是正确有效的，在保证计算精度的前提下，提高了计算效率；②模糊C-means聚类法较K-means聚类法在保证样本准确度上具有优越性。

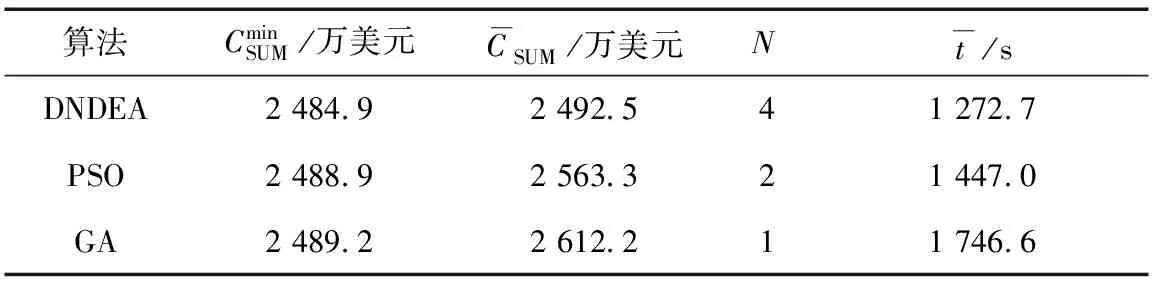
表6 各算法收敛特性对比

6 结论

本文考虑风、光荷间的相关性，分别以年综合费最小和每个场景的配电网运行费最小作为上、下层优化目标，建立了计及AM措施和ADN转供能力的RES双层规划模型。首先，利用模糊C-means聚类法对样本数据进行约简，然后运用DNDEA联合PDIPM的混合方法求解双层规划模型，算例仿真结果表明：

1)通过RES规划，有助于提升系统应对N-1故障的能力和实现故障负荷的有效转供，使得ADN具有了更强的自愈性特征。

2)相对于仅考虑ADN转供能力或仅考虑AM措施的RES规划模型，从综合提高配电网经济性和安全性角度出发，本文规划模型改善效果更明显。

3)AM措施有助于提高ADN中RES的渗透容量，提高配电网的资产利用率，从而减少传统电源的发电量，达到碳减排的目标。

4)RES的合理优化配置对于改善工作点在配电网安全域当中的位置和转供安全裕度的大小具有积极的作用。

5)利用模糊C-means聚类法对样本矩阵进行约简，能够在提高计算效率的同时，保证样本数据的准确性。

[1] 张建华，曾博，张玉莹，等.主动配电网规划关键问题与研究展望[J].电工技术学报，2014，29(2)：13-23. Zhang Jianhua，Zeng Bo，Zhang Yuying，et al.Key issues and research prospects of active distribution network planning[J].Transactions of China Electrotechnical Society，2014，29(2)：13-23.

[2] Li Yujuan，Wang Fanrong.Implementation of smart grid software system based on configurable feeder terminal unit[C]//2012 IEEE Symposium on Electrical & Electronics Engineering，2012：277-280.

[3] De Groot R J W，Morren J，Slootweg J G.Smart integration of distribution automation applications[C]//2012 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies，2012：1-7.

[4] 廖怀庆，刘东，黄玉辉，等.考虑新能源发电与储能装置接入的智能电网转供能力分析[J].中国电机工程学报，2012，32(16)：9-16. Liao Huaiqing，Liu Dong，Huang Yuhui，et al.Smart grid power transfer capability analysis considering integrated renewable energy resources and energy storage systems[J].Proceedings of the CSEE，2012，32(16)：9-16.

[5] 马静，马伟，王增平.基于联络关系的主变故障负荷转供方案[J].电力系统保护与控制，2014，42(19)：1-7. Ma Jing，Ma Wei，Wang Zengping.Power restoration scheme for main transformer fault based on the interconnection relationship[J].Power System Protection and Control，2014，42(19)：1-7.

[6] Martins V F，Borges C L T.Active distribution network integrated planning incorporating distributed generation and load response uncertainties[J].IEEE Transactions on Power Systems，2011，26(4)：2164-2172.

[7] Zhao Yuanyuan，An Yiran，Ai Qian.Research on size and location of distributed generation with vulnerable node identification in the active distribution network[J].IET Generation，Transmission & Distribution，2014，8(11)：1801-1809.

[8] Abapour S，Zare K，Mohammadi-Ivatloo B.Dynamic planning of distributed generation units in active distribution network[J].IET Generation，Transmission & Distribution，2015，9(12)：1455-1463.

[9] Siano P，Chen P，Chen Z，et al.Evaluating maximum wind energy exploitation in active distribution networks[J].IET Generation，Transmission & Distribution，2010，4(5)：598-608.

[10]Zhang Jietan，Fan Hong，Tang Wenting，et al.Planning for distributed wind generation under active management mode[J].International Journal of Electrical Power & Energy Systems，2013，47(6)：140-146.

[11]马瑞，金艳，刘鸣春.基于机会约束规划的主动配电网分布式风光双层优化配置[J].电工技术学报，2016，31(3)：145-154. Ma Rui，Jin Yan，Liu Mingchun.Bi-level optimal configuration of distributed wind and photovoltaic generations in active distribution network based on chance constrained programming[J].Transactions of China Electrotechnical Society，2016，31(3)：145-154.

[12]邓威，李欣然，李培强，等.基于互补性的间歇性分布式电源在配网中的优化配置[J].电工技术学报，2013，28(6)：216-225. Deng Wei，Li Xinran，Li Peiqiang，et al.Optimal allocation of intermittent distributed generation considering complementarity in distributed network[J].Transactions of China Electrotechnical Society，2013，28(6)：216-225.

[13]Zhang Shenxi，Cheng Haozhong，Zhang Libo，et al.Probabilistic evaluation of available load supply capability for distribution system[J].IEEE Transactions on Power Systems，2013，28(3)：3215-3225.

[14]Xiao J，Gu W，Wang C，et al.Distribution system security region：definition，model and security assessment[J].IET Generation，Transmission & Distribution，2012，6(10)：1029-1035.

[15]Xiao Jun，Zu Guoqiang，Gong Xiaoxu，et al.Model and topological characteristics of power distribution system security region[J].Journal of Applied Mathematics，2014(6)：1-13.

[16]Singhee A，Rutenbar R.Why quasi-Monte Carlo is better than Monte Carlo or Latin hypercube sampling for statistical circuit analysis[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2010，29(11)：1763-1776.

[17]Iman R L，Conover W J.A distribution-free approach to inducing rank correlation among input variables[J].Communications in Statistics-Simulation and Computation，1982，11(3)：311-334.

[18]李赢，舒乃秋.基于模糊聚类和完全二叉树支持向量机的变压器故障诊断[J].电工技术学报，2016，31(4)：64-70. Li Ying，Shu Naiqiu.Transformer fault diagnosis based on fuzzy clustering and complete binary tree support vector machine[J].Transactions of China Electrotechnical Society，2016，31(4)：64-70.

[19]Murata R，Endo Y，Haruyama H，et al.On fuzzy C-means for data with tolerance[J].Advanced Computational Intelligence and Intelligent Informatics，2006，10(5)：673-681.

[20]藤春贤，李智慧.二层规划的理论与应用[M].北京：科学出版社，2002.

[21]Storn R，Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11(4)：341-359.

[22]卢扬，吴俊勇，郝亮亮.基于改进MOBPSO算法的含分布式电源的多目标配电网重构[J].电力系统保护与控制，2016，44(7)：62-68. Lu Yang，Wu Junyong，Hao Liangliang.Multi-objective distribution network reconfiguration with distributed generations based on improved MOBPSO algorithm[J].Power System Protection and Control，2016，44(7)：62-68.

[23]Della Cioppa A，De Stefano C，Marcelli A.Where are the niches? Dynamic fitness sharing[J].IEEE Transactions on Evolutionary Computation，2007，11(4)：453-465.

(编辑 赫蕾)

Bi-Level Optimal Renewable Energy Sources Planning Considering Active Distribution Network Power Transfer Capability

LiuJia1XuQian2ChengHaozhong1LanZhou2TianYuan1

(1.Key Laboratory of Control of Power Transmission and Conversion Ministry of Education Shanghai Jiao Tong University Shanghai 200240 China 2.State Grid Zhejiang Electric Power Corporation Economic Research Institute Hangzhou 310008 China)

Under the active management(AM)mode，an optimal Renewable Energy Sources(RES)allocation model is proposed.The model takes the minimum annual total cost and the minimum scenario-based distribution network operation cost as the objectives of upper and lower level，respectively.The power transfer of system fault load and four AM schemes are considered in the optimization formulation.The AM schemes including RES output power resection，RES power factor adjustment，on-load regulating transformer tap adjustment and in-side management measures.Given the randomness of RES output power and load fluctuation，the correlation between wind and light load sample matrix is generated by quasi Monte Carlo simulation and singular value decomposition and then simplified by fuzzy C-means clustering.A hybrid strategy combining dynamic niche differential evolution algorithm and primal-dual interior point method is applied to the model.The compared simulation results demonstrate the effectiveness of the proposed model and method.

Active distribution network，renewable energy sources，bi-level optimal programming，active management，power transfer capability

国家重点研发计划(2016YFB0900102)和国家电网公司科技项目(5211JY16004)资助。

2016-05-10 改稿日期2016-07-12

TM715

刘 佳 男，1991年生，博士研究生，研究方向为电力系统优化、规划、运行。

E-mail：liujia911011@126.com(通信作者)

徐 谦 男，1963年生，硕士，高级工程师，研究方向为电力系统规划和运行。

E-mail：xuqian1963@sina.com