基于条件风险价值的含风电电力系统旋转备用效益研究

刘兴宇 温步瀛 江岳文

(福州大学电气工程与自动化学院 福州 350108)



基于条件风险价值的含风电电力系统旋转备用效益研究

刘兴宇 温步瀛 江岳文

(福州大学电气工程与自动化学院 福州 350108)

由于风电出力的波动性和间歇性，大规模风电并网使得旋转备用效益和风险的矛盾更加突出。考虑系统上、下旋转备用的容量成本和能量成本，以及因购买上旋转备用而减少的失负荷损失和因购买下旋转备用而减少的弃风损失，以期望旋转备用效益最大和系统损失的条件风险价值(CVaR)最小为两个目标，建立基于条件风险价值的含风电电力系统旋转备用效益-风险模型。采用蒙特卡罗法模拟实际负荷功率和风电出力的预测偏差，并改进多目标粒子群优化算法，用于求解得到期望旋转备用效益-风险有效前沿和日前旋转备用计划，以及不同可靠性水平、置信水平对期望旋转备用效益和风险的影响。最后，通过算例验证了该模型和算法的可行性。

旋转备用效益 备用容量 风电并网 条件风险价值 多目标粒子群优化算法

0 引言

大规模的风电并网，对电力系统的可靠性和经济性造成重大的影响[1-3]。系统在购买旋转备用保证系统可靠性的同时，也力求旋转备用产生最大的效益，以及降低系统失负荷和弃风的风险。因此，如何权衡旋转备用效益和风险进行旋转备用容量的制定，是一个值得重视的课题。

针对风电出力的不确定性，风电并网后的系统旋转备用计划应考虑系统的可靠性、经济性和潜在的风险。文献[4，5]提出了旋转备用费用与风险模型来购买含风电电力系统的旋转备用。文献[6，7]引入风险备用，建立含风电电力系统经济调度模型。文献[8]通过类比风险价值(Value at Risk，VaR)和条件风险价值(Conditional Value at Risk，CVaR)，定义风险备用和条件风险备用，作为发电系统运行可靠性度量指标。文献[9]以发电总成本和旋转备用总费用最小为目标，构建基于条件风险方法的电力系统旋转备用模型，但没有考虑失负荷和弃风造成的损失。文献[10]以旋转备用的购买成本最小为目标，在系统安全的机会约束下，构造了确定系统所需最优旋转备用容量的数学模型。文献[11]考虑旋转备用容量成本和停电损失，建立旋转备用成本期望值和条件风险价值多目标优化模型。文献[12]利用风电和负荷的概率密度函数估算系统的停电损失和弃风损失，并将它们作为风险成本计入发电成本目标函数中，求取每台常规机组的目前出力和正负旋转备用量。文献[13]提出了旋转备用成本分析和效益评估的定义及计算方法，并以旋转备用社会效益最大化作为目标函数求解最优旋转备用容量及其分配问题，取得了较好的效果，但未考虑弃风成本和容量成本、下备用成本。上述文献均没有同时考虑系统失负荷和弃风损失、上下旋转备用的容量成本和能量成本等因素，对含风电电力系统旋转备用优化问题进行研究。

旋转备用效益和风险问题属于多变量、非线性的多目标优化问题。而多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization Algorithm，MOPSO)是以粒子群优化算法为基础来解决多目标问题的一种方法，适用于多目标非线性问题的求解，但是算法性能不够，容易陷入局部最优。因此，许多文献对MOPSO算法进行改进。文献[14]对两个子群体分别进行优化，然后交换两个子群的最优解，作为子群速度更新的全局最优解。文献[15]采用轮盘赌局策略选取全局最优。文献[16]在MOPSO中引入粒子间的密集距离机制，提出基于密集距离的MOPSO算法(MOPSO-CD)。文献[17]提出一种多目标纵横交叉算法(MOCSO)，采用粒子两两配对、折中更新、精英保存的策略，缩短了迭代次数。然而由于多目标问题的特殊性，算法还有很大的提升空间，使得多目标粒子群优化算法成为研究热点。

针对以上问题和现有方法的不足，本文考虑系统旋转备用的上、下备用容量成本和上、下备用容量调用量的能量成本以及因购买旋转备用而减少的系统损失(失负荷和弃风损失)。在一定可靠性的前提下，以期望旋转备用效益最大、系统损失的CVaR值最小为目标，建立含风电电力系统的旋转备用效益-风险模型，对含风电电力系统旋转备用效益、系统损失CVaR值进行研究，从而对含风电并网电力系统的旋转备用进行优化。同时，在多目标粒子群优化算法上，提出一种极端值全局最优选择策略，并与其他两种全局最优粒子选择策略相结合来选择全局最优，从而提高该算法的边缘搜索性能，扩大非劣解集的范围。

1 旋转备用效益模型

旋转备用是应对负荷功率和风电出力波动的重要措施之一，但必须权衡系统的可靠性和经济性。若上备用过少，会导致给定的负荷需求不能得到满足，可能造成大量的失负荷，降低了系统的可靠性要求；若下备用过少，会导致多余的风电出力无法接入，可能造成大量的弃风，不利于风电资源的有效利用。而如果旋转备用过多，虽然能提高系统的可靠性并减少失负荷和弃风的发生，但由于旋转备用容量调用率低，可能造成不必要的经济损失。因此，在优化旋转备用时需考虑旋转备用产生的效益，以及系统可能遭受损失的CVaR值。

1.1 旋转备用效益

由于负荷功率和风电出力的随机性和波动性，实际中被调用的旋转备用是不确定的，因此需考虑旋转备用的容量成本和实际备用容量调用量的能量成本[18]。同时，由于负荷功率和风电出力预测偏差的上、下波动，所以需要考虑上备用和下备用。本文定义旋转备用效益为系统减少的损失与旋转备用所需成本之差。其中，系统减少的损失由因购买上备用而减少的失负荷损失和因购买下备用而减少的弃风损失组成，旋转备用所需成本由上、下备用的容量成本和上、下备用容量调用量的能量成本组成。即旋转备用效益为

(1)

式中，Π为系统在24 h内产生的旋转备用效益；Vt、Wt分别为在t时段因购买上备用而减少的失负荷损失和因购买下备用而减少的弃风损失；Cu·t、Bu·t、Cd·t、Bd·t分别为在t时段上备用容量成本和能量成本、下备用容量成本和能量成本。

由于负荷功率和风电出力的预测偏差，使得旋转备用效益很难精确估计，因此本文采用期望旋转备用效益作为旋转备用效益的估计值，即

[Cd·t+E(Bd·t)]}

(2)

式中，E(Π)为系统在24 h内的期望旋转备用效益；E(Vt)、E(Wt)分别为在t时段因购买上备用而减少失负荷损失的期望值和因购买下备用而减少弃风损失的期望值；E(Bu·t)、E(Bd·t)分别为在t时段上、下备用能量成本的期望值。

1)t时段因购买上备用而减少的失负荷损失Vt为

Vt=qLloss·tQLloss·t

(3)

式中，qLloss·t、QLloss·t分别为在t时段单位失负荷损失和因购买上备用而减少的失负荷功率。其中，QLloss·t取t时段上备用的备用容量Ru·t和实际上备用容量需求量Mu·t中的最小值。

QLloss·t=min[Mu·t,Ru·t]

(4)

2)t时段因购买下备用而减少的弃风损失Wt为

Wt=qWloss·tQWloss·t

(5)

式中，qWloss·t、QWloss·t分别为在t时段单位弃风损失和因购买下备用而减少的弃风功率。其中，QWloss·t取t时段下备用的备用容量Rd·t和实际下备用容量需求量Md·t中的最小值。

QWloss·t=min[Md·t,Rd·t]

(6)

3)t时段因购买上、下备用产生的容量成本和能量成本为

Cu·t=ru·tRu·t

(7)

Cd·t=rd·tRd·t

(8)

Bu·t=hu·tHu·t

(9)

Bd·t=hd·tHd·t

(10)

E(Bu·t)=hu·tE(Hu·t)

(11)

E(Bd·t)=hd·tE(Hd·t)

(12)

式中，ru·t、hu·t、rd·t、hd·t分别为在t时段上备用的容量价格和能量价格、下备用的容量价格和能量价格；Hu·t、Hd·t分别为实际上、下备用容量的调用量，其值分别等于QLloss·t和QWloss·t；E(Hu·t)、E(Hd·t)分别为在t时段上、下备用调用量的期望值。

1.2 约束条件

1)备用机会约束。

为了保证系统的可靠性要求，旋转备用须满足一定概率的负荷功率波动和风电出力波动。因此从单个时间段上定义，必须保证单个时段内旋转备用满足系统等效负荷预测偏差的概率不小于某个给定值，即

Pr{Ru·t≥Pt-Pf·t}≥γ

(13)

Pr{Rd·t≥Pf·t-Pt}≥δ

(14)

式中，Pf·t、Pt分别为在t时段系统预测等效负荷和实际等效负荷；可靠性水平γ、δ分别为日前市场的失负荷概率和弃风概率所能允许的上限值。其中，系统预测等效负荷为日前负荷功率预测值与风电出力预测值之差，系统实际等效负荷为实际负荷功率与实际风电出力之差，即

Pf·t=PLf·t-PWf·t

(15)

Pt=PL·t-PW·t=PLf·t+ΔPL·t-(PWf·t+ΔPW·t)

(16)

式中，PLf·t、PWf·t分别为在t时段日前负荷功率预测值和风电出力预测值；PL·t、PW·t分别为在t时段实际负荷功率和风电出力；ΔPL·t、ΔPW·t分别为在t时段负荷功率和风电出力预测偏差，服从一定概率分布的的随机变量。

2)风电场最大有功出力约束。

(17)

2 风电出力和负荷预测偏差概率分布

2.1 风电出力预测偏差概率分布

大多数文献都将风电出力预测偏差近似看成服从正态分布[19]，但文献[20]通过分析某风电场某年的日出力预测偏差，得出风电出力偏差的概率密度曲线，表明风电出力偏差的概率密度分布介于正态分布与拉普拉斯分布之间。因此，本文采用拉普拉斯正态混合分布[21]，建立风电出力偏差ΔPW的概率密度分布函数为

(18)

式中，μW、σW分别为风电出力预测偏差的期望和标准差；ΔPW为风电出力预测偏差的随机变量。

(19)

式中，PWf为风电出力预测值；εW为风电出力预测偏差占预测值的百分比，参照文献[5]取10%；k为峰度(kurtosis)，作为衡量曲线尾端宽度大小的标志[22]，表示为

(20)

式中，E(ΔPW-μW)4为ΔPW的4阶中心矩，参考文献[20]取4.8。

2.2 负荷预测偏差概率分布

(21)

σL=εLPLf

(22)

式中，PLf、ΔPL分别为负荷预测值和预测偏差；σL为负荷预测偏差的标准差；εL为负荷预测偏差占预测值的百分比，参考文献[5]取3%。

3 系统失负荷和弃风损失CVaR模型

3.1 条件风险价值

本文采用在金融领域内被广泛应用的风险计量指标——CVaR。CVaR表示投资损失超过VaR的条件均值[25]，它反映了损失超过阈值时可能遭受的平均水平，体现了投资存在的风险。其基本原理如下[26]：

设X为目标组合可行集，X⊂Rn；令f(x，y)为损失函数。其中，x∈X为决策变量，y∈Rm为决定系统旋转备用需求的不确定随机向量，假设p(y)为y的概率密度函数，对于确定的x，由y引起的损失为f(x，y)。假设α为f(x，y)的临界值，利用蒙特卡罗法模拟样本数据求出y的累计分布函数。设y1，y2，…，ym是y的m个样本，则CVaR的估计值为[27]

(23)

式中，zk=[f(x，yk)-α]+表示max{0，f(x，yk)-α}，zk≥0且zk≥f(x，yk)-α；β为置信水平，β∈(0，1)，表示1-β的概率下，投资者允许其投资组合策略的损失为某一风险水平。

3.2 系统失负荷和弃风损失的CVaR值

因系统实际负荷功率和风电出力的不确定性，使得系统可能遭受失负荷和弃风，造成系统面临失负荷和弃风损失的风险。系统实际等效负荷偏差ΔPSYS·t为系统预测等效负荷减去系统实际等效负荷，即

ΔPSYS·t=Pf·t-Pt=ΔPW·t-ΔPL·t

(24)

1)系统失负荷损失。

当系统实际等效负荷增加，而系统提供的上旋转备用不足时，便会导致失负荷的发生。

(25)

(26)

2)系统弃风损失。

当系统实际等效负荷减少，而系统提供的下旋转备用不足时，便会导致弃风的发生。

(27)

(28)

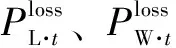
根据上述分析，可得系统失负荷和弃风损失的CVaR值为

zuk≥0,zuk≥fL(x,y)-α1

(29)

zdk≥0,zdk≥fW(x,y)-α2

(30)

式中，fCVaRβ1、fCVaRβ2分别为系统失负荷和弃风损失的CVaR值。

则系统总损失的CVaR值fCVaRβ为系统失负荷损失的CVaR值与系统弃风损失的CVaR值之和，即

fCVaRβ=fCVaRβ1+fCVaRβ2

(31)

因此，本文采用CVaR来度量系统失负荷和弃风损失的风险。

4 旋转备用效益-CVaR模型及求解方法

4.1 旋转备用效益-CVaR模型的目标函数

备用决策者一方面追求期望旋转备用效益的最大化，另一方面追求系统损失的CVaR值最小，但这两目标相互制约，表明效益与风险相互依存的关系。因此，在满足系统给定可靠性的条件下，本文以期望旋转备用效益最大、系统损失的CVaR值最小为两个目标，建立含风电电力系统旋转备用效益-CVaR的多目标模型，即

(32)

不同的期望旋转备用效益对应不同的CVaR值，其中一个目标函数的优化会使得另一个目标函数的目标值降低，因此不存在唯一解同时使该两目标达到最优，而是一组非劣解集。备用决策者根据自身对风险的承受能力和喜好以及对旋转备用效益的期望值制定旋转备用计划。

4.2 基于改进MOPSO的优化模型求解方法

1)全局最优粒子Gbesti的选择策略。

本文采用不同Gbesti选择策略的组合来选择群体中的最优粒子，粒子的全局最优通过三种策略获取：

策略1：从外部档案非劣解集中随机选取一个非支配解作为全局最优，记为gbest1。

策略2：根据外部档案非劣解的密集距离对非支配解进行降序排列(不包括两个端点的密集距离)，从密集距离的前10%中任意选择一个粒子作为全局最优，记为gbest2。

策略3(极端值选择策略)：从非劣解集中的两个极端值中任意选择一个粒子作为全局最优，记为gbest3。

策略1操作简单，但由于每一个非支配解都具有相同被选中的概率，所以会导致粒子较密集的区域选择概率大，不利于全局搜索。策略2提高了密集距离大的粒子被选中的概率，但全局搜索能力还不够。策略3提高了粒子边缘的搜索能力，扩大非支配解集的范围，但不利于Pareto最优边界的分布。因此，本文将这三种选择策略相组合，用于全局最优粒子的选取。

设粒子的个数为m个，在每次迭代中，选择其中a个粒子以gbest1为全局最优，选择其中b个粒子以gbest2为全局最优，选择其中(m-a-b)个粒子以gbest3为全局最优，且a、b满足a+b

2)粒子速度和位置更新。

vi(n+1)=ωvi(n)+c1r1[pbesti-xi(n)]+

c2r2[Gbesti·Zi-xi(n)]

(33)

xi(n+1)=xi(n)+vi(n+1)

(34)

式中，Gbesti为第i个粒子的全局最优向量，Gbesti=[gbest1，gbest2，gbest3]；Zi为系数向量，Zi=[z1，z2，z3]T；pbesti为个体最优粒子；ω为惯性权值；r1和r2为[0，1]之间的随机数；n为当前迭代次数；c1和c2为常数；v为粒子速度；x为粒子位置。由4.2节1)中的分析可知：若i≤a，Zi=[1，0，0]T；若a

3)算法流程。

步骤1：输入负荷和风电基本参数，设定种群规模m、最大迭代次数Maxgen等参数，初始化上、下旋转备用量和速度。

步骤2：计算初始期望旋转备用效益、系统损失的CVaR适应值。

步骤3：根据粒子的支配关系筛选出初始非劣解，存入外部档案非劣解集中。

步骤4：计算非劣解中粒子的密集距离，对其进行降序排列。

步骤5：根据Gbesti的选择策略选取全局最优粒子Gbesti，并根据式(33)、式(34)进行速度和位置更新。

步骤6：计算更新后粒子的适应值，合并更新后的适应值与外部档案中的非劣解，根据非支配关系更新非劣解集。

步骤7：若达到最大迭代次数Maxgen，则停止迭代，输出非劣解；否则，n=n+1，转至步骤4。

采用改进MOPSO算法求解旋转备用效益-CVaR模型的流程如图1所示。

图1 改进MOPSO算法流程Fig.1 Flowchart of improved MOPSO

5 算例计算与分析

5.1 系统参数设置

本文采用文献[28]中得到的预测负荷功率和预测风电出力数据。实际风电出力预测偏差服从拉普拉斯正态混合分布(均值为0，标准差由式(19)计算得到)；实际负荷预测偏差服从正态分布(均值为0，标准差由式(22)计算得到)。根据上述分布，采用Monte-Carlo模拟10 000个实际风电出力偏差和负荷功率偏差。目标函数中，取qLloss·t=1 000元/MW，qWloss·t=3 000元/MW，ru·t=rd·t=112元/MW，hu·t=hd·t=280元/MW[18]。

本文算法参数设置为：种群大小m=300，迭代次数Maxgen=400，a=130，b=130。算法所得结果与MOPSO算法、MOPSO-CD算法和MOCSO算法的结果进行对比分析。

5.2 算法对比与数据分析

MOPSO算法、MOPSO-CD算法、MOCSO算法和本文提出的改进MOPSO算法所得到的最优Pareto有效前沿如图2所示。表1列出了这几种算法和本文算法所得到的Pareto有效前沿端点处的E(Π)和fCVaRβ，即非劣解的近似范围。

图2 最优Pareto有效前沿比较Fig.2 Comparison Pareto-optimal efficient frontier

表1 极端值比较

从图2a中可以看出，本文改进MOPSO算法得到非劣解集的上、下限值范围明显比MOPSO算法和MOPSO-CD算法大。从图2b中可以看出，本文改进MOPSO算法得到非劣解集的下限值比MOCSO算法小。且在相同效益的情况下，本文的改进算法得到的fCVaRβ更小，说明得到的备用计划更优。通过以上分析可知，本文改进的MOPSO算法具有更强的全局搜索能力，搜索到的非劣解集范围更大，更加符合实际的情况。

通过计算，得到在可靠性水平γ、δ都为0.9时，不同置信水平下的E(Π)和fCvaRβ见表2。当置信水平β为0.95时，E(Π)取得最大最小值时的上、下旋转备用容量分配见表3。

表2 不同置信水平β下的E(Π)和fCVaR β

表3 极端值下的旋转备用容量分配

在一定可靠性的前提下，E(Π)和fCVaRβ不可能无限大或无限小，而是具有一定的取值范围。通过计算得出E(Π)∈(42.1，89.4)万元，fCVaRβ∈(0，52.1)万元，分析如下：

1)当旋转备用容量刚好满足系统可靠性约束时，E(Π)和fCVaRβ取得最大值。因为此时系统的旋转备用能够满足大多数系统等效负荷的波动，旋转备用利用率最高；同时，由于旋转备用容量较少，造成较大的失负荷和弃风功率，使得fCVaRβ较大。

2)当旋转备用容量满足系统等效负荷预测偏差的最大值时，E(Π)和fCVaRβ取得最小值。因为此时实际的旋转备用利用率小，过多的旋转备用增大了系统的容量成本；同时，由于系统旋转备用较多，大大降低了失负荷和弃风功率，使得fCVaRβ较小。

综上所述，同时考虑系统上、下旋转备用的容量成本和能量成本，以及因购买上备用而减少的失负荷损失和因购买下备用而减少的弃风损失，能够较全面地反映风电并网后旋转备用对旋转备用效益的影响，更恰当地描述备用计划下的期望旋转备用效益、系统失负荷损失和弃风损失的CVaR值，更符合实际情况。

5.3 置信水平β对E(Π)和fCVaR β的影响

通过改进多目标粒子群算法对算例进行计算，研究不同E(Π)下的fCVaRβ，得到E(Π)-fCVaRβ有效前沿。同时，在给定可靠性的前提下，改变置信水平β，得到不同置信水平β下的E(Π)-fCVaRβ有效前沿，如图3所示。

图3 E(Π)-fCVaRβ有效前沿Fig.3 E(Π)-fCVaRβ efficient frontier

结合表2、表3和图3可以看出：

1)在保证系统给定可靠性的约束下，随着旋转备用的增加，实际中未被调用的备用容量也随之增加，使得E(Π)也随之降低；但由于系统失负荷和弃风的概率降低了，所以fCVaRβ也随之降低。

2)同理，随着E(Π)的增加，fCVaRβ也随之增加，表明E(Π)越大风险也越大，这与实际情况相符。因此，在满足给定系统可靠性的前提下，备用决策者根据自身对风险的承受能力和喜好、以及对旋转备用效益的期望值制定旋转备用计划。

3)置信水平β是备用决策者风险厌恶程度的指标，当β增大时，有效前沿曲线整体左移。说明在相同的风险水平下，置信水平越高则得到的E(Π)越小，即备用决策者风险厌恶度越高则E(Π)就越低；反之亦然。

5.4 可靠性水平γ、δ对E(Π)和fCVaR β的影响

研究置信水平β为0.95，不同可靠性水平γ、δ对E(Π)最大最小值和fCVaRβ的影响，见表4。从表4中可以看出，可靠性水平的变化对E(Π)的最大值和相应的fCVaRβ有影响，而对E(Π)的最小值和相应的fCVaRβ没有影响。

表4 不同可靠性水平下E(Π)和fCVaR β的最值

不同可靠性水平下取得E(Π)max所需旋转备用容量见表5。

表5 不同可靠性水平下E(Π)max所需旋转备用容量

不同可靠性水平γ=δ下，E(Π)的最大值和相应的fCVaRβ随可靠性水平的变化情况如图4所示。

图4 不同可靠性水平下的E(Π)max和fCVaRβFig.4 The E(Π)max and fCVaRβ in different reliability level

结合表4、表5和图4可以看出，改变可靠性水平影响旋转备用容量可选择的范围，从而改变E(Π)和fCVaRβ的范围。系统可靠性水平越高，能够取得的E(Π)max和fCVaRβ越小，对应的旋转备用越大。因为为了保证系统可靠性需增加系统的旋转备用容量，但增加旋转备用降低了系统旋转备用容量的利用率，从而使E(Π)max降低；同时，增加旋转备用容量降低了系统的失负荷和弃风功率，所以fCVaRβ也降低了。即为了保证系统的可靠性降低了旋转备用的经济性，同时降低了系统损失的风险。当可靠性水平低于0.67时，E(Π)max和fCVaRβ保持不变。因为，此时的可靠性要求很低，过少的旋转备用投入达不到E(Π)max最大，因此可以适当地增加旋转备用容量，以达到E(Π)max最大。

6 结论

大规模风电并网给旋转备用计划的制定、旋转备用效益和风险的评估带来了新的挑战。本文围绕系统购买旋转备用产生的效益、系统失负荷和弃风损失的风险，主要工作和结论如下：

1)负荷功率和风电出力的预测偏差给系统增加了旋转备用成本，影响系统运行的经济性和可靠性。本文建立旋转备用效益-风险模型，将旋转备用产生的效益和潜在的损失风险进行评估，更直观地描述旋转备用效益和风险之间的关系。为备用决策者制定旋转备用计划、期望旋转备用效益和风险的评估提供参考。

2)同时考虑系统上、下旋转备用的容量成本和实际容量调用量的能量成本以及因购买旋转备用而减少的失负荷损失和弃风损失，建立旋转备用效益-风险模型，更全面地反映了风电并网后旋转备用对系统旋转备用效益的影响。

3)研究系统的可靠性水平和置信水平对E(Π)和fCVaRβ的影响。系统的可靠性水平越高，可以取得的E(Π)max越低；风险的置信水平越高，fCVaRβ越大，表明备用决策者对风险的厌恶程度越高。

4)对MOPSO进行改进，通过算例对比表明了该方法可以扩大非劣解集的范围，使得备用决策者可以在更大的E(Π)和fCVaRβ范围内，根据自身对风险的承受能力和喜好、以及对旋转备用效益的期望值制定旋转备用计划。

5)本文在假设实际风电出力预测偏差服从拉普拉斯正态混合分布和实际负荷预测偏差服从正态分布的前提下进行旋转备用计划、旋转备用效益和风险研究。若实际情况不满足上述假设时结果将有所不同，有待进一步研究。

[1] 胡国伟，别朝红，王锡凡.考虑运行可靠性的含风电电力系统优化调度[J].电工技术学报，2013，28(5)：58-65. Hu Guowei，Bie Chaohong，Wang Xifan.Optimal dispatch in wind integrated system considering operating reliability[J].Transactions of China Electrotechnical Society，2013，28(5)：58-65.

[2] 蒋程，刘文霞，张建华，等.含风电接入的发输电系统风险评估[J].电工技术学报，2014，29(2)：260-270. Jiang Cheng，Liu Wenxia，Zhang Jianhua，et al.Risk assessment of generation and transmission systems considering wind power penetration[J].Transactions of China Electrotechnical Society，2014，29(2)：260-270.

[3] 杨柳青，林舜江，刘明波，等.考虑风电接入的大型电力系统多目标动态优化调度[J].电工技术学报，2014，29(10)：286-295. Yang Liuqing，Lin Shunjiang，Liu Mingbo，et al.Multi-objeetive dynamic optimal dispatch for large-scale power systems considering wind power penetration[J].Transactions of China Electrotechnical Society，2014，29(10)：286-295.

[4] Wu Junli，Zhang Buhan，Xiao Zhenyin，et al.Application of portfolio theory based on CVaR in determining optimal spinning reserve with consideration of load and wind power uncertainties[J].Advanced Materials Research，2013，724-725：649-654.

[5] Wu Junli，Zhang Buhan，Deng Weisi，et al.Application of cost-CVaR model in determining optimal spinning reserve for wind power penetrated system[J].International Journal of Electrical Power & Energy Systems，2015，66：110-115.

[6] 周玮，孙辉，顾宏，等.计及风险备用约束的含风电场电力系统动态经济调度[J].中国电机工程学报，2012，32(1)：47-55. Zhou Wei，Sun Hui，Gu Hong，et al.Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints[J].Proceedings of the CSEE，2012，32(1)：47-55.

[7] 张新松，礼晓飞，王运，等.不确定性环境下考虑弃风的电力系统日前调度[J].电力系统保护与控制，2015，43(24)：75-82. Zhang Xinsong，Li Xiaofei，Wang Yun，et al.Day-ahead dispatching in consideration of wind power curtailments in uncertain environments[J].Power System Protection and Control，2015，43(24)：75-82.

[8] 周辉，娄素华，吴耀武，等.发电系统一致性运行可靠性指标及其优化模型[J].中国电机工程学报，2009，29(13)：72-79. Zhou Hui，Lou Suhua，Wu Yaowu，et al.Coherent reliability index for generation system operation and its optimization model[J].Proceedings of the CSEE，2009，29(13)：72-79.

[9] 周任军，张浩，范文帅，等.基于条件风险方法的含风电系统旋转备用优化调度[J].电力科学与技术学报，2015，30(1)：3-9. Zhou Renjun，Zhang Hao，Fan Wenshuai，et al.Spinning reserve optimal dispatch in wind power integrated system with CVaR method[J].Journal of Electric Power Science and Technology，2015，30(1)：3-9.

[10]王乐，余志伟，文福拴.基于机会约束规划的最优旋转备用容量确定[J].电网技术，2006，30(20)：14-19. Wang Le，Yu Zhiwei，Wen Fushuan.A chance-constrained programming approach to determine requirement of optimal spinning reserve capacity[J].Power System Technology，2006，30(20)：14-19.

[11]王旭，蒋传文，刘玉娇，等.含大规模风电场的电力系统旋转备用风险决策模型和方法[J].电力系统自动化，2014，28(13)：64-70. Wang Xu，Jiang Chuanwen，Liu Yujiao，et al.Decision-making model and method for spinning reserve and risk of power system integrated with large-scale wind farms[J].Automation of Electric Power Systems，2014，28(13)：64-70.

[12]赵晋泉，唐洁，罗卫华，等.一种含风电电力系统的日前发电计划和旋转备用决策模型[J].电力自动化设备，2014，34(5)：21-27. Zhao Jinquan，Tang Jie，Luo Weihua，et a1.Day ahead generation scheduling and spinning reserve decision-making model for powerd containing wind power[J].E1ectric Power Automation Equipment，2014，34(5)：21-27.

[13]张国全，王秀丽，王锡凡.电力市场中旋转备用的效益和成本分析[J].电力系统自动化，2004，24(21)：14-18. Zhang Guoquan，Wang Xiuli，Wang Xifan.Study on benefits and costs of spinning reserve capacity in power market[J].Automation of Electric Power Systems，2004，24(21)：14-18.

[14]王司令，宋保维，段桂林.某型AUV对转电机子群协同多目标粒子群优化[J].电工技术学报，2015，30(5)：135-141. Wang Siling，Song Baowei，Duan Guilin.Optimization design of an AUV’s motor with counter-rotating rotors based on the collaborative multi-objective particle swarm algorithm[J].Transactions of China Electrotechnical Society，2015，30(5)：135-141.

[15]Coello A C，Pulido G T，Lechuga M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation，2004，8(3)：256-279.

[16]Raquel C R，Naval P C.An effective use of crowding distance in multi-objective particle swarm optimization[C]//Genetic and Evolutionary Computation Conference，Washington，2005：257-264.

[17]孟安波，李专.采用多目标纵横交叉算法的电力系统动态环境经济调度[J].电力系统保护与控制，2016，44(2)：109-115. Meng Anbo，Li Zhuan.Dynamic environmental economic dispatch of power system adopting multi-objective crisscross optimization algorithm[J].Power System Protection and Control，2016，44(2)：109-115.

[18]谭伦农，张保会.市场环境下的事故备用容量[J].中国电机工程学报，2002，22(11)：54-58. Tan Lunnong，Zhang Baohui.Reserve capacity for failure in power market environment[J].Proceedings of the CSEE，2002，22(11)：54-58.

[19]Doherty R，Malley M O.A new approach to quantify reserve demand in systems with significant installed wind capacity[J].IEEE Transactions on Power Systems，2005，20(2)：587-595.

[20]Bludszuweit H，Dominguez-Navarro J A，Llombart A.Statistical analysis of wind power forecast error[J].IEEE Transactions on Power Systems，2008，23(3)：983-991.

[21]Jones P N，Mclachlan G J.Laplace-normal mixtures fitted to wind shear data[J].Journal of Applied Statistics，1990，17(2)：271-276.

[22]葛炬，王飞，张粒子.含风电场电力系统旋转备用获取模型[J].电力系统自动化，2010，34(6)：32-36. Ge Ju，Wang Fei，Zhang Lizi.Spinning reserve model in the wind power integrated power system[J].Automation of Electric Power Systems，2010，34(6)：32-36.

[23]周双喜，王海超，陈寿孙.风力发电运行价值分析[J].电网技术，2006，30(14)：99-102. Zhou Shuangxi，Wang Haichao，Chen Shousun.Analysis on operation value of wind power resources[J].Power System Technology，2006，30(14)：99-102.

[24]卢志刚，刘艳娥，马丽叶，等.基于安全等级的电网最优安全经济域研究[J].电工技术学报，2015，30(20)：210-218. Lu Zhigang，Liu Yane，Ma Liye，et al.The optimal security and economic region study based on the security hierarchy[J].Transactions of China Electrotechnical Society，2015，30(20)：210-218.

[25]Rockafellar R T，Uryasev S.Conditional value-at-risk for general loss distributions[J].Journal of Banking and Finance，2002，26(7)：1443-1471.

[26]王壬，尚金成，冯旸，等.基于CVaR风险计量指标的发电商投标组合策略及模型[J].电力系统自动化，2005，29(14)：5-9. Wang Ren，Shang Jincheng，Feng Yang，et al.Combined bidding strategy and model for power suppliers based on CVaR risk measurement techniques[J].Automation of Electric Power Systems，2005，29(14)：5-9.

[27]Rockafellar R T，Uryasev S.Optimization of conditional value-at-risk[J].Journal of Risk，1999，29(1)：1071-1074.

[28]卢鹏铭，温步瀛，江岳文.基于多时间尺度协调机组组合的含风电系统旋转备用优化研究[J].电力系统保护与控制，2015，43(5)：94-100. Lu Pengming，Wen Buying，Jiang Yuewen.Study on optimization of spinning reserve in wind power integrated power system based on multiple timescale and unit commitment coordination[J].Power System Protection and Control，2015，43(5)：94-100.

(编辑 赫蕾)

Study on the Benefit from Spinning Reserve in Wind Power Integrated Power System Based on Conditional Value at Risk

LiuXingyuWenBuyingJiangYuewen

(College of Electrical Engineering and Automation Fuzhou University Fuzhou 350108 China)

Due to the fluctuation and intermittent of wind power，large-scale wind power grid connection makes the contradiction between the spinning reserve benefit and risk more prominent.The capacity cost and the energy cost of the system up and down spinning reserve，the reduced power loss due to the purchase of up spinning reserve and the reduced wind loss due to the purchase of the down spinning reserve are considered.To establish the spinning reserve benefit-risk model of wind power integrated system based on conditional value at risk(CVaR)with the goal of maximum expected spinning reserve benefit and minimum CVaR value of system loss.Monte Carlo method is used to simulate the actual load power and wind power prediction error，and the multi-objective particle swarm optimization algorithm is improved to find the efficient frontier of expected spinning reserve benefit-risk and the day-ahead spinning reserve plan，and the influence of different reliability level and confidence level on expected spinning reserve benefit and risk.Finally，the example shows the feasibility of the model and the algorithm.

Spinning reserve benefit，reserve capacity，wind power integration，conditional value at risk(CVaR)，multi-objective particle swarm optimization algorithm(MOPSO)

福建省自然科学基金项目资助(2013J01176)。

2016-03-27 改稿日期2016-04-25

TM614

刘兴宇 男，1990年生，硕士研究生，研究方向为电力市场和电力系统优化运行等。

E-mail：n140120023@fzu.edu.cn(通信作者)

温步瀛 男，1967年生，教授，硕士生导师，研究方向为电力市场和电力系统优化运行等。

E-mail：wenby87@fzu.edu.cn