基于三维有限元法的基坑排水井渗流量计算方法

2017-05-16沈振中张凤翔

水力发电 2017年3期

关键词：柱面剖分水头

马莹,沈振中,张凤翔

(1.淮委沂沭泗水利管理局,江苏徐州221000；2.河海大学水利水电学院,江苏南京210098)

基于三维有限元法的基坑排水井渗流量计算方法

马莹1,沈振中2,张凤翔1

(1.淮委沂沭泗水利管理局,江苏徐州221000；2.河海大学水利水电学院,江苏南京210098)

准确分析基坑渗流场、预测排水井渗流量,对合理布置基坑工程防渗排水系统,确保基坑渗流稳定和工程安全有重要意义。根据实际工程应用的需要,研究了基于三维渗流有限元法任意断面渗流量计算方法,提出了采用任意柱面网格,计算复杂基坑井群排水量的数值计算方法,研制了基于三维有限元法的基坑排水井渗流量计算程序,并应用于某水电站厂房基坑开挖施工的排水量计算分析中。结果表明,该计算方法具有良好的适用性和准确性。

基坑；渗流；渗流量；三维有限元法；排水井

0 引言

水利工程、桥梁隧道工程等深基坑较多,深基坑施工条件复杂,工程难度大。为了保证干地施工,常需要采用排水井降低基坑地下水位。基坑开挖以后,由于地下水的渗流作用,基坑容易造成边坡失稳,引发滑坡等灾害,基坑底部渗水,影响施工进度,严重时还会引起坑底隆起,诱发安全事故[1]。为此,对基坑进行渗流分析十分必要。渗流分析的主要内容之一就是预测渗流量,以确定排水设施的容量。目前基于有限元法的数值模拟在基坑渗流分析中占主导地位,且经过工程实践验证,三维有限元法数值模拟可较好地反映基坑渗流场实际的状况。

基于有限元法的渗流量计算主要有中断面法[2]和等效结点流量法[3]。前者计算原理简单且很容易通过程序实现,但由于水头函数数值解为数值离散解,且实际选用的过流断面为各个单元的中断面,因此当计算区域材料分区和地质条件复杂时,单元形状很不规则,其中断面也是极不规则的扭曲面,所计算的渗流量的准确性较低,有时不能满足工程应用的要求,特别是在设有排水井群的基坑渗流场分析中,若采用中断面法计算单井渗流量,则必须在每个排水井周围布置柱状辐射向网格,这对于基坑渗流控制方案优化计算分析而言,剖分网格的工作量极大,故中断面法实际上难以应用。后者有效地提高了渗流量计算精度。等效结点流量法将任一过流断面上的渗流量表示成相关单元的传导系数与相应结点水头的乘积的代数和,避免了对水头离散解的进一步求导运算,所求得的渗流量计算精度与水头解的计算精度同阶,但其缺点是相关单元的传导系数的准确性还难以确定,所得到的断面渗流量为代数和,并不能准确地表达通过任一断面法向的渗流量。同样,对于设有排水井群的基坑渗流而言,该法也存在同样的问题。为此,沈振中等[4]提出了计算任意断面渗流量的插值网格法,该法首先对任意给定的四边形断面自动剖分形成细密网格,然后通过插值获得该断面网格节点的水头,并计算得出各断面网格形心处的渗透坡降,最后计算通过断面的法向渗流量。插值网格法的优点是计算精度高,不受三维有限元网格的限制,应用方便。但在计算基坑排水井的渗流量时,采用平面插值网格仍然存在困难。因此,本文在计算任意断面渗流量的插值网格法基础上,提出了一种采用任意柱面网格计算复杂条件下基坑排水井群排水量的数值计算方法,可适用于多井、任意剖分网格基坑排水井渗流量计算问题,可以方便、准确地求得基坑排水井的渗流量,为基坑排水系统布置的设计和施工提供参考。

1 计算渗流量基本方程

在三维渗流场中,设流管截面积足够小,取互相靠近的2个平面S1和S2,作用水头以2个面形心处的水头h1与h2表示,2个面之间的距离为L,根据达西定律,通过该流管的渗透流量为

Q=-KAdH/ds=KA(h1-h2)/L

(1)

式中,K为介质的渗透系数；A为流管截面积。如果L趋于0(相对于面积A足够小),则可以把计算得到的渗流量看作为通过截面S1和S2的渗流量[4]。

2 排水井渗流量数值计算方法

对于单个排水井,若三维有限元网格采用以井为中心的辐射向布置,则计算排水井的渗流量可以采用中断面法。但是对于任意六面体剖分的三维有限元网格,中断面法已不能适用。这里给出一种采用柱面网格的排水井渗流量数值计算方法,可用于任意六面体剖分的三维有限元网格计算的渗流场,排水井可以考虑尺寸大小,也可以忽略其大小,置于单元节点处。设三维渗流场中任一排水井WW’,已知排水井的位置和大小如图1所示。该三维渗流场已由有限元法计算求得各单元节点的位势,现计算该井的排水量。首先以该井为中心轴,以任一合适的半径取一柱面,建立整体计算坐标系下的柱面方程,即(x-x0)2+(y-y0)2-r2=0,然后对该柱面进行剖分,离散成四边形单元。当剖分的网格足够细密时,由四边形网格构成的面近似为柱面。根据计算所需的精度要求,将该柱面离散成细密的四边形网格。如图1所示,柱面竖直向划分为60个单元,径向划分为72个单元,即离散后的柱面网格为4 320 个单元。为计算渗透坡降,需要考虑2个距离足够小的同轴柱面,这样构成的六面体单元如图2所示,面1- 4- 8- 5为S1i,面2- 3- 7- 6为S2i,2个面之间的距离为Li,取中断面abcd,其面积为Ai,根据式(1),只要得到S1i与S2i形心处的水头h1i与h2i,即可得到通过该单元的渗流量Qi。那么通过整个柱面的总渗流量为

(2)

式中,n为剖分的小单元数；ki为第i个单元沿径向的渗透系数,由该单元形心处的材料特性确定。

图1 圆柱面离散单元网格

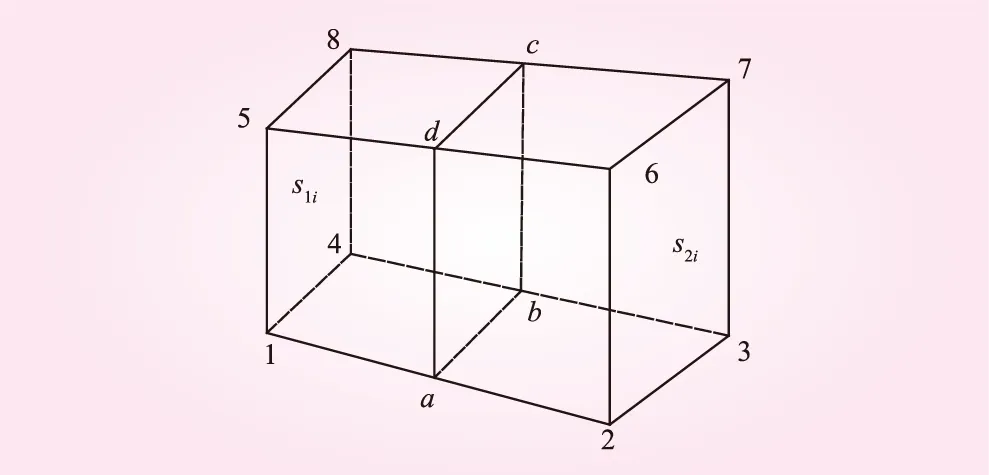
图2 柱面单元计算流量示意

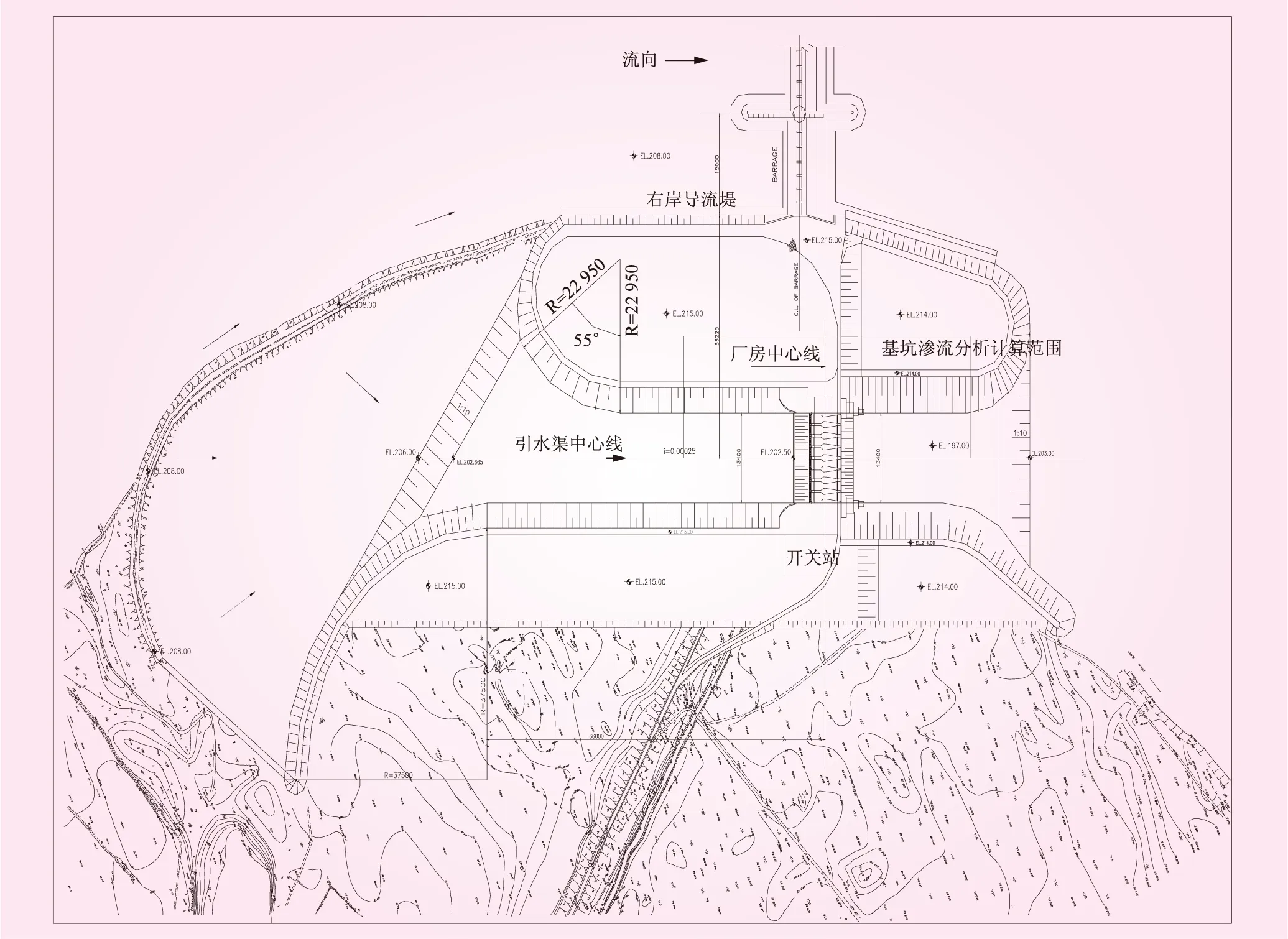
图4 某水利枢纽平面布置

对于同轴两个柱面均匀剖分的情况,任意2个单元中S1i与S2i的距离都相同,即Li=L,且各个单元的面积也相等,故式(2)可简化为

(3)

式(3)表明,计算通过该任意柱面的渗流量,关键要计算任一柱面单元各节点的水头值h1i与h2i,于是该问题就转化为如何求解三维渗流场中指定柱面任意一点的水头值的问题。

渗流分析通常采用空间八结点六面体等参数单元。假设某点在单元中,如图3所示,在求得三维渗流场后,可得到各单元结点的水头值,则点A的水头hA为

(4)

式中,hi(i=1,2,3,…,8)为8个结点的水头值；Ni(ξ,η,ζ)为用局部坐标表示的单元形函数。利用等参数变换,采用牛顿迭代法通过搜索所有空间单元即可求得[4]。

另外,采用任意断面插值网格法可以计算排水井底面的渗流量,与计算得到的柱面网格的渗流量相加,即可得到排水井的全部渗流量。

图3 空间八结点六面体单元示意

3 应用实例

3.1 工程概况

某水利枢纽由引水渠、厂房、尾水渠和开关站等组成。渠道纵轴线位于闸堤右侧362.25 m。上游设计最高水位211.5 m,正常蓄水位211.50 m。电站按径流式电站运行。电站装机容量96 MW,最大水头6 m,设计水头4.8 m,最小水头3.2 m。该工程水电站厂房、挡水建筑物设计洪水标准为百年一遇洪水设计,千年一遇洪水校核。枢纽平面布置如图4所示。

厂房区为砂砾石基础,地下水埋深约2 m,砂砾石层的渗透系数为0.10～0.16 cm/s。为了保证混凝土浇筑和厂房基础处理干地施工,需对厂房基础及施工期基坑抽排水系统计算分析,并采取相应的防渗、抽水和排水措施,确保厂房基础不会发生渗流破坏,保证工程顺利施工。

由于厂址区地下水位高,砂砾层渗透系数大,经初步计算,工程施工期基坑渗透流量在80万m3/d左右,要保证干地施工,仅采用简单的基坑防渗或排水系统难以实现,需要防渗、排水同时考虑且合理布置。因此,施工期基坑防渗和排水布置非常复杂,初步设计共16种计算工况。首先,计算各工况下基坑的渗透流量,选择满足干地施工的方案；然后,对满足条件的方案进行比较,优选安全经济的方案；最后,对优选方案进行调整,提出最优方案,给出位势分布、渗透坡降、渗透流量和单井排水量等成果。

在确定基坑防渗和排水布置方案时,需要计算多种工况下基坑排水井群的总渗流量,还需要计算各排水井的单井渗流量,以供选择排水设备技术参数。如采用中断面法和改进等效结点流量法,均需要先确定井群的布置,并对每个排水井周围的单元进行特殊处理,剖分成辐射状的单元,才能计算单井的渗流量。由于每个方案排水井的位置和数量都是变化的,因此,这种方法会大大增加建立有限元模型的工作量。采用任意断面渗流量的插值网格法,不需要根据井群的布置对每个工况或方案重建有限元模型,只需将排水井布置在不同的结点上[4]。但该法受“断面为平面”的限制,不能计算单井渗流量,而采用本文方法则不需要重建有限元模型,即可直接计算基坑中所有排水井的单井渗流量。

施工期基坑防渗及排水布置方案较多,这里仅对最终确定出的基坑抽排水布置优化方案进行简要介绍,并计算各排水井渗流量。该方案设排水井共70口,深21 m,井径0.8 m,旋喷防渗墙深28 m,排水井布置如下为引水渠(动力渠道)轴线布置第1口井,沿河流方向基坑上下游两侧每间隔约8 m各布置1口,共46口；垂直河流方向,自基坑厂房轴线开始每间隔约9 m各布置1口,共24口。具体布置见5。

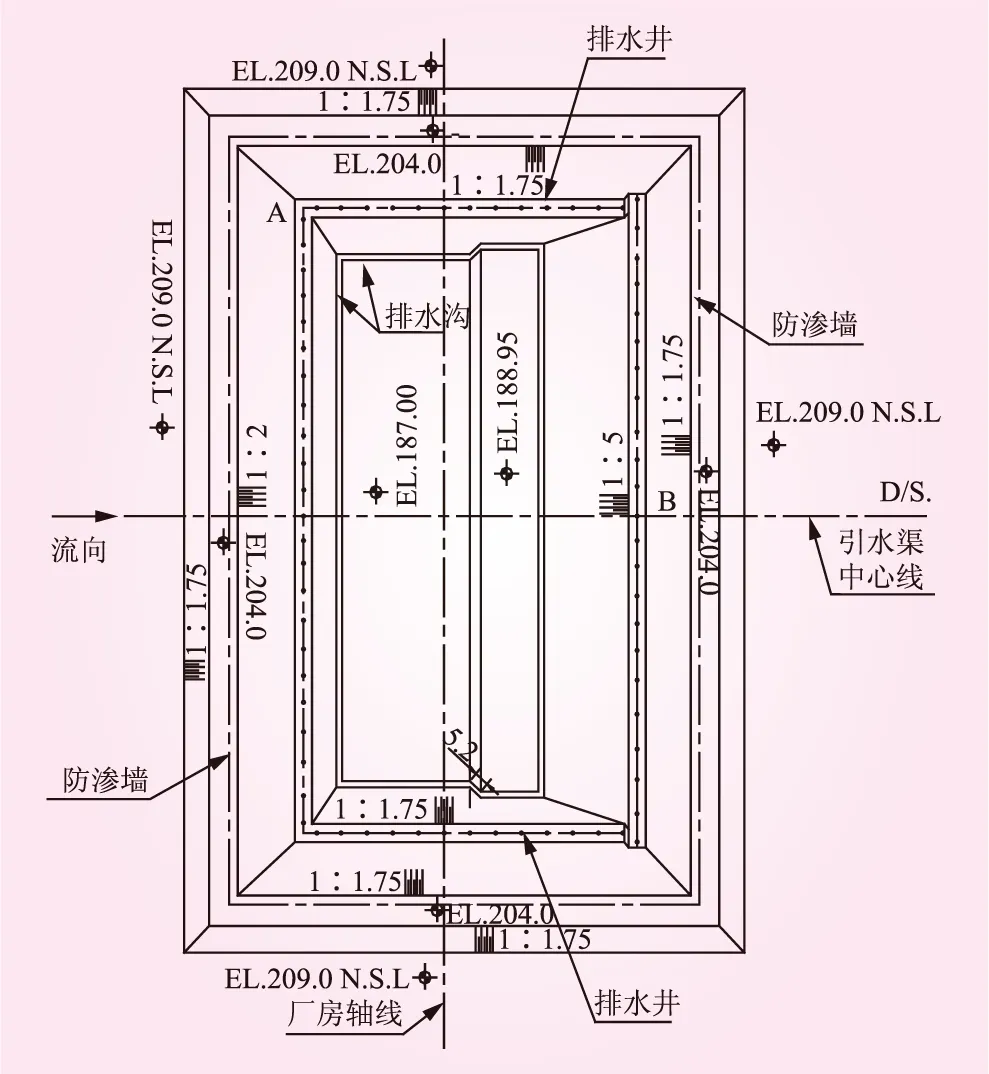
图5 施工期基坑开挖平面布置

3.2 排水井渗流量计算分析

渗流场计算分析取引水渠轴线左侧靠近河流的一半基坑,并自基坑外沿向外取约350 m,施工期基坑附近地下水位等值线如图6所示。采用本文方法,采用的柱面为以排水井中心为轴线,半径为3 m,轴向网格大小为0.3 m,圆周向为3°,计算各排水井渗流量的结果见表1,总渗流量为56.68×104m3/d。在基坑排水井外侧布置规则网格,采用中断面法计算总渗流量,其结果为57.92×104m3/d。本文通过计算单井渗流量得到的基坑总渗流量与中断面法计算的总渗流量相差较小,相对误差2.2%,故本文计算方法的精度可以满足工程应用要求。

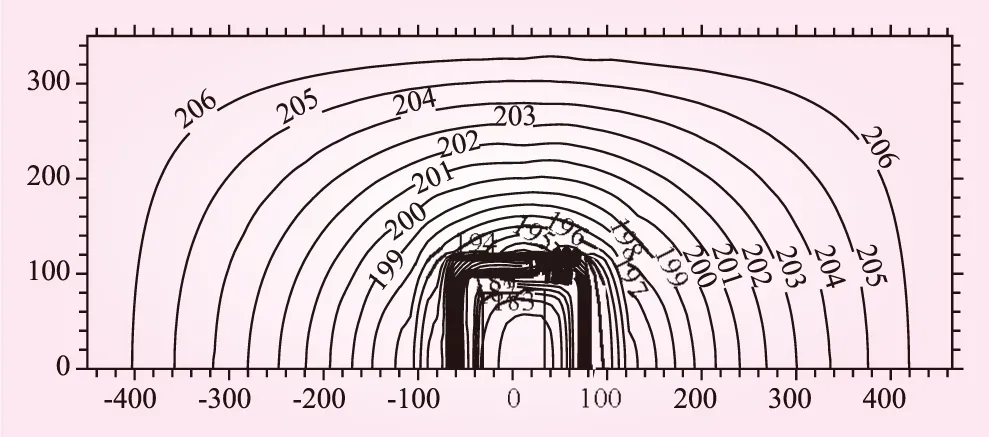
图6 基坑附近地下水位等直线(单位：m)

从计算结果可知,基坑各排水井渗流量并不相同,最大渗流量为355.412 m3/h,位置坐标(-45.00,85.0),位于基坑上游角点A,该部位地下水位较高；最小渗流量为313.441 m3/h,位置坐标(66.80,17.0),位于基坑下游动力渠道中心线处,该部位地下水位较低。最大渗流量与最小渗流量相差41.071 m3/h,分别位于沿河流方向的上、下坡,第11口排水井靠近印度河,在基坑角点附近,水力梯度较大,故渗透流量比较大[5- 8]；第34口排水井在印度河下坡,靠近引水渠轴线处,此处水力梯度最小,故渗透流量较小。

表1 优化方案排水井渗流量计算结果

4 结语

根据实际工程应用要求,提出了根据排水井轴线和半径建立柱面网格的算法,并参照计算任意断面渗流量的插值网格法,运用有限元提出了排水井渗流量的计算方法,并研制相关的计算程序。采用提出的方法计算了某枢纽工程基坑防渗排水优化布置方案的各排水井的渗流量,并进行分析,结果表明利用本文方法不需要根据井的布置重新剖分三维有限元网格,可大大减少工作量,计算结果也更为准确,该方法具有很强的实用性。

[1]裴桂红, 刘建军, 李继祥, 等. 深基坑开挖中渗流-应力耦合数值模拟[J]. 岩石力学与工程学报, 2004, (S2)： 4975- 4978．

[2]丁家平. 有限元法的渗流量求解及渗流图像的自动化绘制[J]. 水利水运工程学报, 1987(2)： 81- 89．

[3]朱岳明. Darcy渗流量计算的等效结点流量法[J]. 河海大学学报, 1997, 25(4)： 105- 108．

[4]SHEN Zhenzhong, XU Liqun, CUI Juan, et al. A new interpolation meshing method for calculating seepage flux of well[C]∥The 3rdInternational Conference on Bioinformatics and Biomedical Engineering(ICBBE2009), Beijing, China, 2009．

[5]KUKLIK P. Several comments on influence zone depth progress in deep hole foundation[C]∥GeoShanghai International Conference 2006, Underground Construction and Ground Movement, 2006: 355- 362．

[6]纪佑军, 刘建军, 薛强. 基坑地下水渗流数值模拟[J]. 武汉工业学院学报, 2006, 25(1): 72- 77．

[7]庞景兰. 基坑开挖工程中渗流场的三维有限元分析[J]. 水科学与工程技术, 2006(2)： 24- 26．

[8]姜忻良, 宗金辉. 基坑开挖工程中渗流场的三维有限元分析[J]. 岩土工程学报, 2006, 28(5): 564- 568．

[9]卢廷浩. 土力学[M]. 南京：河海大学出版社, 2005.

[10]沈振中. 基于变分不等式理论的渗流计算模型研究[D]. 南京：河海大学, 1993．

[11]BAIOCCHI C, BREZZI F, COMINCIOLI, V. Free boundary problem in fluid flow through porous media[C]∥ICAD, 2nd International Symposium on Finite Element Methods in Flow Problems, Italy, 1976: 14- 18．

[12]BAIOCCHI C, FRIEDMAN A. A filtration problem in a porous medium with variable permeability[J]. Annali di Matematica Pura ed Applicata, 1977, 114(4): 377- 393．

(责任编辑王琪)

Calculation Method of Seepage Flow for Drainage Wells of Foundation Pit Based on 3-D FEM

MA Ying1, SHEN Zhenzhong2, ZHANG Fengxiang1

(1. The Yi-Shu-Si River Basin Administration, Xuzhou 221000, Jiangsu, China;2. College of Water Conservancy and Hydropower, Hohai University, Nanjing 210098, Jiangsu, China)

Accurate analyses of foundation seepage field and prediction of seepage flow of drainage wells are important for reasonably arranging drainage system of foundation engineering and maintaining the stability of foundation pit as well as the safety of engineering. According to the needs of actual engineering, the calculation method based on 3D FEM is used for analyzing the seepage flow of a certain profile. A numerical method to compute the displacement of complex foundation pit is also proposed by using arbitrary cylindrical mesh wells. A computer code for counting the seepage flow of pit drainage wells is developed based on FEM and has been applied to the calculation and analyses of drainage flow in the foundation pit excavation of a hydropower station. The results show that the method has good applicability and accuracy．

foundation pit; seepage; seepage flow; 3D FEM; drainage well