耗散鸡群算法在水库优化调度中的应用

2017-05-16魏月梅池丽敏

水力发电 2017年3期

关键词：公鸡母鸡雏鸡

魏月梅,池丽敏

(1.江苏苏盛工程造价咨询有限公司，江苏南京210029；2.南京市水利规划设计院股份有限公司,江苏南京210006)

耗散鸡群算法在水库优化调度中的应用

魏月梅1,池丽敏2

(1.江苏苏盛工程造价咨询有限公司，江苏南京210029；2.南京市水利规划设计院股份有限公司,江苏南京210006)

基于鸡群算法运行过程中易于陷入停滞状态的不足,提出了一种基于耗散结构的鸡群算法,并以水库优化调度模型为基础,将耗散鸡群算法应用于解决水库优化调度问题。对比分析不同算法的水库调度实例优化结果可知,基于耗散结构的鸡群算法求解水库优化调度问题是行之有效的。

水库优化调度；鸡群算法；耗散结构；全局寻优能力；收敛速度

0 引言

20世纪50年代初,R.E.Bellman等人在研究多阶段决策过程的优化问题时,提出了著名的最优性原理,创立了解决这类过程优化问题的新方法——动态规划(DP)[1],并得以广泛的研究与应用。但随之出现的优化过程中动态规划的状态空间和决策空间约束易产生“维数灾”等不足,促使一些学者研究出了解决更多非线性优化问题的新算法——群体智能优化算法,如最早提出并得以广泛应用的遗传算法(GA)[2]、蚁群算法(ACO)[3]、粒子群算法(PSO)[4],以及最近新兴的人工蜂群算法(ABC)[5]、人工鱼群算法(AFSA)[6]、蝙蝠算法(BA)[7]。这些群体智能算法为解决大量存在于众多领域的复杂非线性全局优化问题提供了新的求解思路。

鸡群算法(CSO)最早是由MENG Xianbing等人集合粒子群算法(PSO)、遗传算法(GA)、蝙蝠算法(BA)等的优化特性,模拟鸡群生活规律，抽象化得出的一种新型群体智能算法[8]。2015年,孔飞等人对上述鸡群算法(CSO)中小鸡的位置更新公式进行了相关改进,进一步证实该算法在求解高维优化问题时,更容易找到全局最优值,且相对于其他进化算法而言有明显的优越性[9]；2016年,洪杨等人提出了基于杂交的改进鸡群算法,并将改进的鸡群算法用于多分类器系数的优化,降低了错误率,缩短了训练时间[10]；崔东文利用鸡群算法搜寻投影寻踪模型最佳投影方向,建立鸡群优化算法-投影寻踪洪旱灾害评估模型,该方法可有效提高评估精度,避

免最佳投影方向寻优结果变化范围过大的缺陷[11]；许仪勋等人在对鸡群算法进行改进后,将其运用于识别各个家电的工作状态研究中,具有较高的负荷识别准确率和广泛的适用性[12]。然而,鸡群算法作为一种新型的群体智能算法,目前在水库优化调度研究领域中还未得以应用。因此,本文针对鸡群算法及其在水库优化调度领域中的具体应用问题展开研究,探讨鸡群算法应用于水库优化调度领域的可行性和有效性。

1 鸡群算法

1.1 基本原理及步骤

鸡群算法(CSO)是通过模拟鸡群觅食行为而得到的一种随机智能优化算法。实际鸡群觅食过程中,往往存在着多组鸡群,每组鸡群中均存在着严格的等级制度。将各组鸡群划分为公鸡、母鸡和雏鸡3个等级。其中,母鸡跟随公鸡觅食,雏鸡则在母鸡周围觅食,故公鸡在种群中起着领导性作用。相应的,公鸡在食物竞争中具有最大优势,母鸡次之,而雏鸡则处于最不利地位,故需要一起生活的,具有母子关系的母鸡对雏鸡加以保护。鸡群中各个个体所具有的优势性能则通过其所在位置对应的目标函数适应值来表示。同时,根据适应值对鸡群进行等级划分,种群中最优个体所处于的空间位置即为待优化问题的最优解。

设觅食空间为D维，觅食鸡群可随机划分为G组，每组鸡群所含个体总数量为N。其中，公鸡数量为R，母鸡数量为H，雏鸡数量为M。

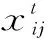
(1)

(2)

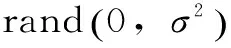
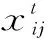
(3)

(4)

(5)

式中，rand为[0,1]上均匀分布的随机数；r为第i只母鸡在其所属组群中的公鸡配偶；s为在整个鸡群中随机选取的除第r只公鸡外的任1只公鸡；fi、fr、fs分别为第i、r、s只公鸡对应的适应值。上述过程既体现了公鸡在鸡群中的领导作用，又体现了不同鸡群之间的协同觅食行为。

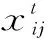
(6)

式中，m为第i只雏鸡所追随的母鸡(雏鸡与母鸡的母子关系随机建立)；F为雏鸡追随母鸡觅食行为所体现的个体差异性。上述过程体现出由于雏鸡觅食能力有限，故只局限于在母鸡周围进行觅食。

待鸡群中各个个体均完成一次完整的觅食行为后,及时按照每只鸡所处位置对应适应值的大小重新对种群进行等级划分,以体现鸡群中雏鸡成长为公鸡或母鸡及母鸡孵化后代等行为,然后再按照上述公式展开鸡群的觅食行为,依次循环。

1.2 基于耗散结构的鸡群算法

通过上述基本鸡群算法的原理介绍及相关文献[8-12]中的研究成果可知,鸡群中存在的等级制度使得整个鸡群以公鸡为主,母鸡与雏鸡均可看似借鉴公鸡的觅食经验进行觅食。故当公鸡陷入局部优值时,将导致整个鸡群陷入一种看似平衡的停滞状态,在一定程度上削弱了该算法的优化性能。

相对于上述平衡状态,耗散结构则在一定条件下可使非孤立系统在远离平衡态的过程中,经过突变而形成新的有序结构。任小波等[13]最先将耗散结构引入到智能算法中,提出了耗散粒子群算法,并取得了较好的研究成果。为此,本文将耗散结构融入到鸡群算法中,提出耗散鸡群算法(HCSO),对公鸡按照式(1)进行觅食行为后加以改进如下

(7)

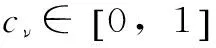
由式(7)可知，cν决定着公鸡的觅食位置是否发生突变，即起着决定性作用，故cν决定着该耗散结构的性能。cν取值较大时，会导致鸡群中大部分公鸡发生突变，使得鸡群丢失觅食经验而变为无序状态；cν取值较小时，鸡群中只有小部分公鸡发生突变，使得耗散结构未能发挥作用。根据前人研究经验，本文取cν=0.1。

2 水库调度鸡群算法设计

2.1 目标函数

水库优化调度问题多以发电量最大为优化目标,其数学表达式为

(8)

式中，E为水电站的最大发电量；K为水电站的综合出力系数；qi为第i时段的发电流量；Hi为第i时段的发电水头；Δti为第i时段所对应的时间长度；T为划分的时段数。

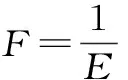
2.2 约束条件

水量平衡约束可表示为

(9)

式中，Vt+Δt、Vt分别为水库在第t+Δt、t时刻的库容；Qr、Qy、Qf、Qq分别为水库在Δt时间内的入库流量、区间引流量、发电流量、弃水流量。

流量约束可表示为

Qmin≤Qout≤Qmax

(10)

式中，Qout为水库在Δt时间内的出库流量；Qmin、Qmax分别为相关部门所要求的水库向下游放水的最小流量，以及保证下游防洪安全所允许的最大下放流量。

水位约束可表示为

Zmin≤Zt≤Zmax

(11)

式中，Zt为水库在第t时刻末的水库水位；Zmin、Zmax分别为考虑兴利与安全需要水库在第t时刻允许达到的最低与最高水位。

出力约束可表示为

Nmin≤Nt≤Nmax

(12)

式中，Nt为水电站在第t时段内的平均出力；Nmin、Nmax分别为水电站的最小允许出力(多设为保证出力)、最大允许出力(多设为装机容量或预想出力)。

2.3 求解步骤

应用鸡群算法求解水库优化调度问题的求解步骤如下：

(1)种群初始化。将水库各时段末所对应的蓄水位Z=(z1,z2,…,zT)设定为D(本文中D即为T)维觅食空间中鸡群的各个体所处位置xi=(xi1,xi2,…,xiD)。根据水位约束条件，对各个个体的初始位置按照下式进行随机赋值，并记迭代次数t=0。即

(13)

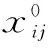
(2)种群等级划分。将上述初始化得到的鸡群随机划分为G组，并根据各组鸡群中各个个体所处位置计算其相应的适应值fi=(xi)，并以此为依据，对各组鸡群内部进行等级划分。其中，适应值相对最优的个体规划为公鸡，适应值相对最弱的个体规划为雏鸡，其他的则为母鸡。

(3)群体觅食。种群中的各公鸡按照式(1)、(7)、各母鸡按照式(3)、各雏鸡按照式(6)依次展开觅食，进行位置更新。

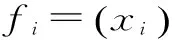
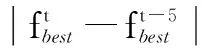
(6)输出结果。输出鸡群中最优个体所处的位置和对应的适应值，即水库各时段末所对应的蓄水位Z=(z1,z2,…,zT)和相应的最大发电量的倒数，并将上述数据转换成所需形式。

3 实例验证

在文献[9]、[11]中,运用鸡群算法优化基准函数的仿真实验,证实了该算法具有较好的寻优效果与执行能力。本文直接将鸡群算法应用于水库优化调度问题,研究其可行性与有效性。

3.1 水库资料

本文研究实例为一综合年调节水库,该水库的水位与库容关系、下游水位与流量关系、来水过程线均已知。水库正常蓄水位704 m,死水位685 m,6月初至8月底为汛期,要求水位不超过695 m。水电站的设计保证出力为7.8万kW,装机容量为30万kW,综合出力系数为8.5。合理安排水库的各月月末水位,使整个调度期的发电量达到最大。

3.2 优化结果分析

为合理验证鸡群算法的可行性与有效性,本文同时采用目前应用较为广泛的动态规划算法(DP)、粒子群算法(PSO)对上述水库调度问题进行优化,并对比各算法的寻优效果。各算法参数设置如下：动态规划算法(DP)对水位可行域离散100点；粒子群算法(PSO)中学习因子c1=2、c2=2,最大、最小惯性权重分别为ωmax=1.4、ωmin=0.4；鸡群算法(CSO)中鸡群G=10组,每组个体数量N=100,公鸡数量R=0.3N,母鸡数量H=0.6N,雏鸡数量M=0.1N,F∈[0.5,0.9]；耗散鸡群算法(HCSO)各参数同鸡群算法(CSO)。此外,突变因子cν=0.1。各智能算法的最大迭代次数均选取1 000次,并进行30次独立重复试验，目标函数与约束条件均相同。各算法寻优结果对比见表1。

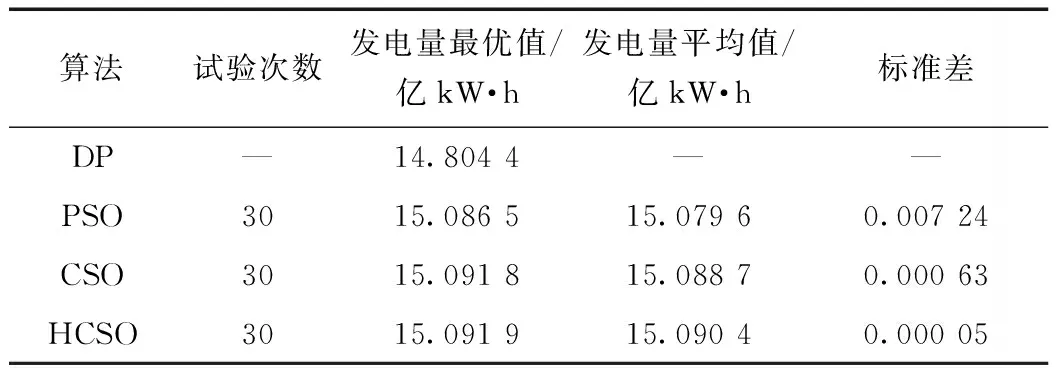
表1 各算法寻优结果对比

由表1可知,与动态规划算法(DP)、粒子群算法(PSO)相比,鸡群算法(CSO)寻优结果的最优值、平均值、标准差均表现出明显的优势,即该算法在解决水库优化调度问题时表现出良好的优化性能与稳定性能,故应用鸡群算法(CSO)求解水库优化调度问题是可行的；②与基本鸡群算法(CSO)相比,本文所提出的耗散鸡群算法(HCSO)寻优结果的平均值与标准差有着明显的提升,即有效的帮助原算法在寻优过程中脱离了看似平衡的停滞状态,对原鸡群算法所做的改进是有效的。

各算法的收敛速度见图1,从图1可知,耗散鸡群算法(HCSO)与鸡群算法(CSO)均可以在迭代次数为800次左右时达到较优的寻优效果。即在相同的优化环境中,上述算法可以在相对较小的迭代次数下寻得优值,节省了求解时间。在固定的优化环境及迭代次数下,耗散鸡群算法(HCSO)的寻优效果相对最优,对原鸡群算法所做的改进有效地提升了该算法的寻优能力与收敛速度。

图1 收敛速度对比

4 结语

鸡群算法是根据生物群体生活的启发而得到的一种新型群体智能算法,与基本优化算法相比,有较好的全局搜索能力与收敛速度。但该算法在实际运行过程中易于陷入暂时的平衡而处于停滞状态。为此,本文提出了基于耗散结构的鸡群算法。

与动态规划算法、粒子群算法相比,鸡群算法在解决水库优化调度问题时表现出良好的优化性能与稳定性能,应用该算法求解水库优化调度问题是可行的,且本文所提出的基于耗散结构的鸡群算法有效提升了原鸡群算法的全局寻优能力与收敛速度。

[1]李端, 钱富才, 李力, 等. 动态规划问题研究[J]. 系统工程理论与实践, 2007, 8(8)： 56- 64．

[2]HOLLAND J H. Adaptation in natural and artificial systems[M]. Ann Arbor: University of Michigan Press, 1975．

[3]张纪会, 徐心和. 一种新的进化算法——蚁群算法[J]. 系统工程理论与实践, 1999, 19(3)： 84- 87.

[4]樊玮. 粒子群优化方法及其实现[J]. 航空计算技术, 2004, 34(3)： 39- 42．

[5]KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Erciyes University, 2005．

[6]LI X L, SHAO Z J, QIAN J X. An optimizing method based on autonomous animats∶fish-swarm algorithm[J]. Systems Engineering Theory and Practice, 2002, 22(11)： 32- 38．

[7]程春英, 刘娜仁. 蝙蝠算法的研究进展[J]. 电脑知识与技术, 2016, 12(24)： 187- 198．

[8]MENG X B, LIU Y, GAO X Z, et al. A new bio-inspired algorithm: chicken swarm optimization[C]∥5th International Conference on Swarm Intelligence. Hefei: Springer International Publishing, 2014: 86- 94．

[9]孔飞, 吴定会. 一种改进的鸡群算法[J]. 江南大学学报：自然科学版, 2015, 14(6)： 681- 688.

[10]洪杨, 于凤芹. 改进的鸡群算法并用于多分类器系数优化[J/OL]. 计算机工程与应用, [2016- 02- 16]. http:∥www.cnki.net．

[11]崔东文. 鸡群优化算法-投影寻踪洪旱灾害评估模型[J]. 水利水电科技进展, 2016, 36(2)： 16- 23．

[12]许仪勋, 李旺, 李东东, 等. 基于改进鸡群算法的非侵入式家电负荷分解[J].电力系统保护与控制, 2016, 44(13)： 27- 32．

[13]任小波, 杨忠秀. 耗散粒子群算法的性能分析[J]. 计算机仿真, 2010, 27(2)： 204- 207．

(责任编辑杨健)

Application of Dissipation Chicken Swarm Optimization in Reservoir Optimal Operation

WEI Yuemei1, CHI Limin2

(1. Jiangsu Susheng Engineering Cost Consulting Co., Ltd., Nanjing 210029, Jiangsu, China;2. Nanjing Water Planning and Designing Institute Co., Ltd., Nanjing 210006, Jiangsu, China)

To overcome the shortage of Chicken Swarm Optimization that easily falling into a standstill in the process of running, an improved Chicken Swarm Optimization based on dissipative structure theory is proposed and this Dissipation Chicken Swarm Optimization is applied to solve reservoir optimal operation problem on the basis of reservoir optimal operation model. The comparison and analyses on the optimization results of different reservoir scheduling algorithms show that the application of Dissipation Chicken Swarm Optimization in solving reservoir optimal operation problem is effective．

reservoir optimal operation; Chicken Swarm Optimization; dissipative structure; global optimization ability; rate of convergence