大渡河中下游梯级水电站模拟优化运行研究

梁楚盛,邹祖建,黄炜斌,马光文

(1.四川大学水利水电学院,四川成都610065；2.国电大渡河流域水电开发有限公司,四川成都610041)

大渡河中下游梯级水电站模拟优化运行研究

梁楚盛1,邹祖建2,黄炜斌1,马光文1

(1.四川大学水利水电学院,四川成都610065；2.国电大渡河流域水电开发有限公司,四川成都610041)

针对梯级水电站中长期来水不确定性的问题,依据长系列确定来水情况下的优化调度结果,建立门限回归、最近邻抽样回归和BP人工神经网络优化调度函数模型,模拟大渡河中下游梯级水电站的联合优化运行,将各模型的模拟优化调度结果与来水确定下的最优运行水位进行对比。结果表明,BP人工神经网络优化调度函数模型能够更好的模拟梯级水电站运行,对梯级水电站的实际优化运行具有参考意义。

梯级水电站；优化运行；门限回归；最近邻抽样回归；BP人工神经网络

0 引 言

为了提高大渡河干流河段的水资源利用效率,增加大渡河梯级水电站的发电收益,研究梯级水电站的联合优化运行非常重要。本文选取了大渡河中下游的大岗山(260万kW)、瀑布沟(360万kW)、深溪沟(66万kW)、枕头坝一级(72万kW)、龚嘴(77万kW)和铜街子(62.5万kW)等6座梯级水电站,研究梯级水电站的联合优化运行。其中,具有中长期调节能力的瀑布沟水电站水库正常蓄水位为850 m,死水位790 m,其他水电站均为周调节或者日调节水电站。

目前,梯级水电站联合优化运行面临的最大问题是天然来水不确定,中长期预报准确度不高。受入库流量不确定性的影响,传统的中长期优化调度模型在实际优化运行中受到制约[1]。为减少中长期来水不确定性的影响,本研究采用1956年～2015年的大渡河中下游历史径流资料进行优化调度计算,计算周期和计算时段分别为年和旬,得到历年瀑布沟水电站水库的最优运行方式[2]。根据每个时段的历年最优运行方式建立优化调度函数模型,单独分析各个时段的优化运行,将年优化运行问题分解为每个时段的优化运行问题。本研究分别建立了门限回归、最近邻抽样回归和人工神经网络3种优化调度函数模型,模拟大渡河中下游梯级水电站的优化运行。

1 优化调度函数模型

1.1 样本获取

大渡河中下游梯级水电站群主要利用目标是发电。为提高水电枯水期发电积极性,四川电网实行水电丰枯上网电价政策。本研究结合丰枯电价政策,选择梯级年发电效益最大作为优化目标[3- 5]。

(1)目标函数。表达式为

(1)

式中,E为整个梯级水电站的年发电收入；Qi,t为第i座电站在第t时段发电流量；ui,t为第i座水电站在第t时段耗水率；T为年内计算总时段数(以旬为计算时段,T=36)；N为梯级水电站总数(N=6)；Mt为第t时段的小时数；Pt第t时段的电价。

(2)水量平衡约束。公式为

Vi,t+1=Vi,t+(qi,t-Qi,t-Si,t)Δt∀t∈T

(2)

式中,Vi,t、Vi,t+1分别为第i个水电站第t时段初末水库蓄水量；qi,t、Si,t分别为第i个水电站第t时段入库流量和弃水流量；Δt为计算时段长度。

(3)水库蓄水量约束。公式为

Vit,min≤Vit≤Vit,max∀t∈T

(3)

式中,Vit,min、Vit,max分别为第i个水电站第t时段水库最小和最大蓄水量。

(4)水库下泄流量约束。表达式为

Qit,min≤Qi,t≤Qit,max∀t∈T

(4)

式中,Qit,min、Qit,max分别为第i个水电站第t时段最小和最大允许下泄流量。

(5)电站出力约束。公式为

Ni,min≤Qi,t/ui,t≤Ni,max

(5)

式中,Ni,min为第i个水电站的允许的最小出力；Ni,max为第i个水电站的装机容量。

(6)梯级联合运行最小出力约束。表达式为

(6)

式中,Nmin为梯级水电站群联合运行的最小保证出力。

非负条件约束：上述所有变量均为非负变量(≥0)。

边界条件：①初末水位。考虑到梯级联合运行最小出力约束,瀑布沟水电站的初末水位如果定为正常蓄水位,在来水不充裕的年份将不能满足梯级联合运行最小出力约束。本研究将瀑布沟水电站的初末水位定为845 m。②负荷率水平。考虑当前四川省电力市场供大于求、汛期水电站存在弃水问题,梯级水电站无法长时间满发,对汛期的负荷率采用80%进行计算。③分时电价。大渡河中下游梯级水电站各时期上网电价见表1。

表1 大渡河中下游梯级水电站上网电价 元/(kW·h)

在VS2010平台上,采用C#语言实现动态规划算法对模型的求解。对1956年～2015年的长系列径流资料进行优化计算,得到1956年～2015年瀑布沟水电站水库各时段的水位,记为最优运行水位。从历史最优运行水位中选择每个时段瀑布沟水电站水库的最高水位作为上包线,最低水位作为下包线,包线内的区域为瀑布沟水电站的最优水位运行区(见图1)。

图1 瀑布沟水电站水库最优水位运行区

从图1可知,瀑布沟水电站库水位从每年年初开始逐渐消落,进入汛期之前(即5月底)消落到最低水位,然后开始慢慢蓄水,到9月底蓄到正常蓄水位。进入10月以后,每年的最优运行水位基本保持在正常蓄水位。因此,10月上旬至12月下旬,瀑布沟水电站以正常蓄水位作为最优运行水位；而1月上旬至9月下旬,每个时段的历史水位变幅很大,每个时段的末水位主要受时段初水位和时段入库流量的影响。以时段初末水位和入库流量作为变量构建优化调度函数模型,对以瀑布沟水电站为控制性水库的梯级水电站群联合优化运行意义重大。

1.2 建立调度函数模型

以瀑布沟水电站水库时段初水位和入库流量作为自变量,时段末水位作为因变量建立优化调度函数。即

(7)

式中,Zt,Zt+1分别为瀑布沟水电站水库第t时段的初水位和末水位；Qt为第t时段的入库流量。

(1)门限回归模型。以瀑布沟水电站的时段入库流量Qt为门限变量,时段初水位Zt为自变量,时段末水位Zt+1为决策变量,建立门限回归调度函数模型。即

(8)

(2)最近邻抽样回归模型。以1956年～2005年的样本数据作为抽样样本,定义为特征向量Di=(Zi,t,Qi,t)(i=1,2,…,50),Zi,t+1为Di对应的后续值。以2006年～2015年的样本数据为检验样本,定义当前特征向量Dj=(Zj,t,Qj,t)(j=51,52,…,60),Zj,t+1为Dj对应的后续值。其中

(9)

式中,K为最近邻数；Zn(i,t+1)表示与当前特征向量最邻近的第n个样本对应的后续值；Wn表示第n个样本的权重。

(3)人工神经网络模型。采用1956年～2005年的样本数据作为训练样本,以Zt+1作为样本输出,Zt、Qt作为样本输入,构建梯级蓄水BP人工神经网络模型。模型包括输入层、中间隐层和输出层,根据试算结果,当隐层神经元数为3时，收敛程度比较好。

2 模型求解

2.1 门限回归模型

(10)

两段的组内方差和为

(11)

组间方差为

B2=V2-S2

(12)

2.2 最近邻抽样回归模型

(13)

计算抽样样本后续值的权重Wn,并计算当前特征向量对应的后续值。即

(14)

2.3 BP人工神经网络

BP人工神经网络通过不断的训练,对网络模型的权值和阈值进行调整[6]。训练过程见图2。

图2 BP人工神经网络调度函数计算流程

隐含层的传递函数为tansig函数。即

(15)

输出层的传递函数为pureline函数。即

Y=f(Net(2),θ(2))=Net(2)+θ(2)

(16)

式中,Y为网络输出；Net(2)为输出层的输入；θ(2)为输出层阈值。

3 模拟计算结果与分析

本文针对优化调度函数模型进行求解,得到模拟调度水位过程线。表1为检验期(2006年～2015年)瀑布沟水电站4月中旬优化调度函数模型得到的时段末水位与最优运行水位。

表2 模拟时段末水位与最优运行水位对比 m

通过与最优运行水位进行对比,得到优化调度函数模型每个时段的相对误差et。即

(17)

用相对误差et表示各优化调度函数的模拟优化调度结果与最优运行水位的拟合程度[7]。误差统计结果见表3。从表3可知,在枯水期和平水期,优化调度函数的模拟优化调度结果很接近最优运行水位,丰水期模拟优化调度结果相对较差。3种优化调度函数模型中,BP人工神经网络模型误差相对较小,模拟优化调度结果更加接近最优运行水位,能够更好的模拟梯级水电站优化运行。

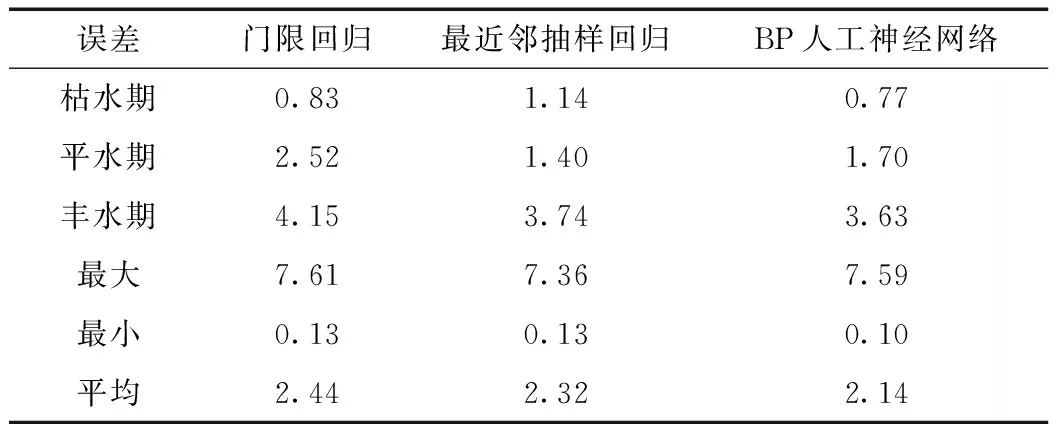
表3 优化调度函数模拟误差 %

4 结 语

通过与来水确定情况下的最优水位过程线综合对比可知,本文建立的优化调度函数模型模拟梯级水电站联合运行具有可行性,尤其是在枯期和平水期,模拟优化调度误差很小。3种优化调度函数中,BP人工神经网络模型能够更好的模拟梯级水电站优化调度运行,建立BP人工神经网络优化调度函数模拟优化调度,对梯级水电站的中长期优化运行具有参考意义。

[1]纪昌明, 周婷, 王丽萍, 等. 水库水电站中长期隐随机优化调度综述[J]. 电力系统自动化, 2013, 37(16)： 129- 135．

[2]卢立宇, 赵飞, 陶春华, 等. 瀑布沟水电站及下游梯级经济运行方式研究[J]. 水力发电, 2015, 41(4)： 63- 65．

[3]李基栋, 黄炜斌, 马光文. 雅砻江下游梯级水库隐随机联合优化调度函数研究[J]. 水电能源科学, 2014, 32(12)： 49- 53．

[4]周佳, 马光文, 张志刚. 基于改进POA算法的雅砻江梯级水电站群中长期优化调度研究[J]. 水力发电学报, 2009, 28(1)： 1- 4．

[5]纪昌明, 李克飞, 张验科, 等. 梯级水电站群联合调度多目标风险决策模型[J]. 水力发电, 2013, 39(4)： 61- 64．

[6]王金龙, 马光文, 黄炜斌, 等. BP人工神经网络模型在溪洛渡、向家坝两库联合优化调度规则中的应用[J]. 水电能源科学, 2012, 30(12)： 48- 51．

[7]缪益平, 纪昌明. 运用改进神经网络算法建立水库调度函数[J]. 武汉大学学报： 工学版, 2003, 36(1)： 42- 44, 58．

(责任编辑 杨 健)

内蒙古芝瑞抽水蓄能电站可行性研究报告通过审查会

2017年1月12日至14日，内蒙古芝瑞抽水蓄能电站可行性研究报告通过水电水利规划设计总院审查。会议审查认为，报告达到了可行性研究阶段勘测设计工作内容和深度的要求，基本同意该报告。

内蒙古芝瑞抽水蓄能电站位于内蒙古自治区赤峰市克什克腾旗芝瑞镇境内，距赤峰市约110 km。电站装机容量1 200 MW。工程建成后将承担蒙东电网调峰、填谷、调频、调相及紧急事故备用等任务。枢纽工程主要由上水库、下水库、输水系统、地下厂房和地面开关站等建筑物组成。上水库采用沥青混凝土面板全库盆防渗，堆石坝最大坝高73 m；下水库主要有拦沙坝、拦河坝两座沥青混凝土心墙坝、泄洪排沙洞和放空洞，最大坝高分别为27、34 m。

2014年9月，内蒙古芝瑞抽水蓄能电站预可行性研究报告通过审查。可行性研究阶段北京勘测设计研究院继续深入开展勘察、试验和设计研究工作，先后完成了大量专题设计研究报告等设计成果，并通过有关主管部门的审查和批复。在上述勘测设计研究成果的基础上，2017年1月，北京院编制完成了《内蒙古芝瑞抽水蓄能电站可行性研究报告(送审稿)》。

(刘超)

Research on Optimal Operation of Cascade Hydropower Stations in Middle and Lower Reaches of Dadu River

LIANG Chusheng1, ZOU Zujian2, HUANG Weibin1, MA Guangwen1

(1. College of Water Resource and Hydropower, Sichuan University, Chengdu 610065, Sichuan, China;2. Dadu River Hydropower Development Co., Ltd., Chengdu 610041, Sichuan, China)

In view of the uncertainty of long-term inflow condition for cascade hydropower stations, the Threshold Regression model, Nearest Neighbor Bootstrapping Regressive (NNBR) model and BP Artificial Neural Network (BP-ANN) model are established respectively based on long series optimal operation results of stations to simulate the optimization operation of cascade hydropower stations in middle and lower reaches of Dadu River. The optimization operation simulation results of each model are compared with long-term optimal operation under certain inflow condition. The result proves that the BP Artificial Neural Network model is closer to optimal operation and can provide reference for the practical operation of cascade hydropower stations．

cascade hydropower station; optimal operation; Threshold Regression; Nearest Neighbor Bootstrapping Regressive(NNBR); BP-Artificial Neural Network

2016- 09- 20

国家重点基础研究发展计划(“973”计划)资助项目(2013CB036406- 4)；中国清洁发展机制基金赠款项目(2013114)

梁楚盛(1993—),男,湖南岳阳人,硕士研究生,研究方向为水利电力经济管理．

TV737

A

0559- 9342(2017)03- 0098- 04