运用相似三角形解决平衡问题
2017-05-16李煜星
李煜星


摘要:在研究受力问题时,选取不同的方法求解。但是,有关长度和力的问题、非特殊三角形问题、看似条件不足的动态平衡问题、已知角或求角问题等,根据笔者三十多年的教学经验来看,运用相似三角形解决上述类型的题目比较好,相对比较简单。
关键词:相似三角形;长度和力;平衡;非特殊三角形;角
中图分类号:G633.7 文献标识码:A 文章编号:1992-7711(2017)03-0086
当所选研究对象受三个力时,用合成法求未知力,画出平行四边形,根据已知条件不同,选取不同的方法求解。以下几种情况用相似三角形法比较好,相似三角形法是通过力的三角形与几何三角形相似求未知力。
一、有关长度和力的问题
解三角支架习题时常有两种已知条件给法,一种是已知边长,另一种是已知角,都是求力,但解法不同,当然这类题用正交分解法也可以解出。
例1. 在三角架上的B点用一根细绳挂在一个重为G的物体,如图1所示,求横梁AB 和斜梁BC受l到的力各为多大?已知三角架AB=L1,Bc=L2,横梁AB水平。(解略)
例2. 如图2所示,长为5 m的细绳的两端,分别系于竖直在地面上相距为4m的两竖直杆的两端A、B上,绳上挂一光滑的轻质挂钩,其下拴住一个重为12N的物块,平衡时绳中的张力 F=
解:如图3,连CD,作绳中张力两个 F(即F1=F2)的合力与重力等大反向,对角线相互平分且垂直,很显然θ1= θ2=θ,力的三角形与长度三角形相似,由長度三角形可得OC+OD=(OA+OB)sinθ,所以sinθ=4/5,由力的三角形可得 F=(G/2) cosθ=5G/6=10N。
二、非特殊三角形问题
例3. 一个表面光滑的半球形物体国定在水平面上,在其球心 O的正上方一定高度处国定一个小滑轮,一根细绳的一端拴一小球,置于球面上 A点,另一端绕过定滑轮,如图4所示。现缓慢地拉动细绳的另一端,使小球沿球面从A点拉到B点,在此过程中,小球所受球面的支持力 FN 及细绳对小球的拉力FT的变化化情况是:
A. FN变大,FT变小;
B. FN变小,FT变大;
C. FN不变,FT变小;
D. FN变大,FT变小;
解:小球缓慢上移,可认为小球始终处于平衡状态,故小球所受拉力FT 与小球所受支持力FN的合力跟小球的重力G等值反向,即FT与FN的合力应竖直向上,大小恒为 G,支持力FN与球面垂直,FN的作用线通过两球心,小滑轮光滑,细线上各点张力大小相等,因三个力FN、FT、G组成三角形与ΔAOC 相似即可求解。
在小球上升的过程中,AO与CO的长度保持不变,只有AC的长度逐渐减小,可见拉力FT变小,支持力FN大小保持不变,故选项C正确。
点评:本题从物理思想上看,上面的解法称为平衡法或合成法,从数学方法上看,称为相似三角形法。可见,若为特殊三角形教学中用三角函数就可以解出且较简便,而非特殊三角形用相似三角形法更简单。
三、看似条件不足的动态平衡问题
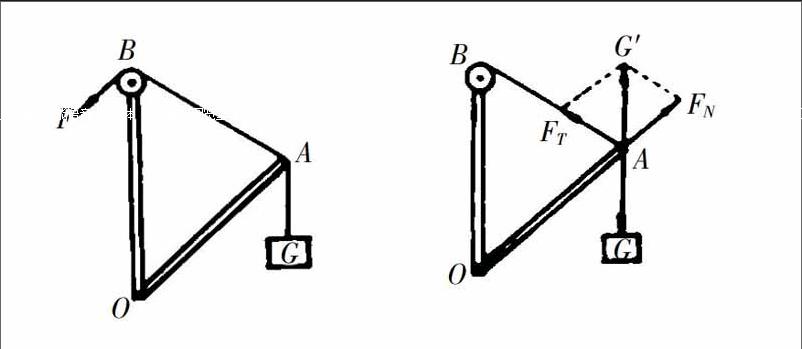
例4. 如图6所示,竖直杆OB顶端有光滑轻质滑轮,轻质杆OA自重不计,可绕O点自由转动,OA=OB。当细绳缓慢放下,使∠AOB由O0逐渐增大到1800的过程中(不包括),下列说法正确的是:
A. 绳上的拉力先逐渐增大后逐渐减小;
B. OA杆上的压力先逐渐减小后逐渐增大;
C. 绳上的拉力越来越大,但不超过2G;
D. OA杆上的压力大小始终等于G;
解:作出结点 A的受力分析图,如图7所示, 即可知绳的拉力 F始终小于2G。
四、己知角或求角的问题
一般来说,已知角或求角的问题,我们都比较习惯于正交分解法,但有些问题用相似三角形法更简单。
例5. 一个重为 G的小环套竖直放置的半程为R的光滑大圆环上,一个劲度为k,原长为 L(L<2R)的轻弹簧,一端固定在大圆环顶点 A,另一端与小环相连,小环在大圆环上可无摩擦活动,小环静止于B 点时,如图8所示,求弹簧与竖直方向的夹角。
解:小环受到重力 G,方向坚直向下,受到弹簧弹力的作用线一定与AB 重合。根据平衡条件不难判断,弹簧是处于伸长状态,弹力只能沿BA方向指向A,大环对小环的作用力是沿着半径方向斜向下,重力 G与FN的合力与弹簧的作用力F是一对平衡力,由几何关系得:AB=2Rcosθ,
再由三角形相似,对应边成比例可得
(作者单位:内蒙古包头市一机一中 014030)