中式烹饪用时间温度积分器的构建与验证

邓 力，黄德龙，彭 静，汪 孝，崔 俊，曾雪峰，何腊平

（贵州大学酿酒与食品工程学院，贵阳 550025）

中式烹饪用时间温度积分器的构建与验证

邓 力，黄德龙，彭 静，汪 孝，崔 俊，曾雪峰，何腊平

（贵州大学酿酒与食品工程学院，贵阳 550025）

蛋白质变性能够较广泛地表征烹饪加热品质变化，因而寻找到一种z值为7.36 ℃的耐高温α-淀粉酶，与蛋白质热变性z值 5～10 ℃相近。以该酶溶液为指示剂，在玻璃毛细管中封装后置入烹饪耐受性高的、特定形状的魔芋凝胶（g-KGM）载体，从而构建了烹饪研究用时间温度积分器（time temperature integrators，TTIs）装置。随后，在模拟烹饪过程而设定的对流传热条件下，通过传热学试验结合非稳态传热以及酶失活动力学数学模型计算得到剩余酶活，与 TTIs装置指示剂酶活实测值比较，两者误差小于2.24%。进一步，应用该TTIs装置测定了实际烹饪爆炒过程的表面换热系数。所构建的TTIs装置，结合数值模拟，可以分析测量常规试验传热学方法无法应用的激烈烹饪中流体-颗粒的传热过程，也可应用于其他领域的移动颗粒传热学研究。

传热学；温度；酶；中式烹饪；时间温度积分器；温度-时间关系；表面换热系数

邓 力，黄德龙，彭 静，汪 孝，崔 俊，曾雪峰，何腊平. 中式烹饪用时间温度积分器的构建与验证[J]. 农业工程学报，2017，33(7)：281－288.doi：10.11975/j.issn.1002-6819.2017.07.037 http://www.tcsae.org

Deng Li, Huang Delong, Peng Jing, Wang Xiao, Cui Jun, Zeng Xuefeng, He Laping. Establishment and verification of time-temperature integrators for Chinese cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(7): 281－288. (in Chinese with English abstract)doi：10.11975/j.issn.1002-6819.2017.07.037 http://www.tcsae.org

0 引 言

时间温度积分器（time temperature integrators，TTIs）定义为用于模拟热处理过程中的目标质量参数温度时间总体变化效果的小型装置，由指示剂和载体食品模拟物组成，其中指示剂应与食品受热关键品质因子具有相近的动力学参数，食品模拟物与食品具有相近且稳定的热物理性质和形状[1]。因而TTIs能够表征加热对食品品质的影响，TTIs结合数学模型可以对流体-食品颗粒传热开展传热学和品质动力学分析[2-3]。国外关于TTIs在食品热处理中的应用较为广泛，用于研究罐头杀菌、液体颗粒超高温杀菌等工艺中温度-时间关系的变化[4-8]。

中式烹饪的发展趋势是实现烹饪的标准化、自动化，必须把握烹饪传热-品质变化的内在原理。文献[9-10]提出了烹饪品质形成的传热学和动力学数学模型，证明温度对烹饪品质具有决定作用，而加热品质变化动力学是联系温度和品质的纽带。烹饪过程中食品颗粒处于非稳态传热状态[9]，温度随空间位置和时间变化，测量难度很大。目前获取液体-颗粒传热中颗粒内部温度-时间关系的方法有近10种[11]，而应用较多的是热电偶法[12]、数值模拟法[13]和TTIs法[14]。热电偶法只能对静态颗粒的温度进行测量。数值模拟法通过求解非稳态传热方程获取温度-时间关系，具有省时、受试验条件限制较小等优点，但该方法的关键参数，如流体-颗粒表面换热系数hfp，必须由试验测定[15-16]。爆炒是中式烹饪的典型工艺[17]，过程短促剧烈，有些仅持续10 s，由于强烈搅拌导致颗粒快速移动，因此热电偶法不适用于爆炒烹饪研究，数值模拟方法也受限于无法试验测定hfp。而TTIs装置可以将食品模拟物载体做成与烹饪颗粒原料类似的形状，置于烹饪原料中共同加热，最终通过检测指示剂的不可逆变化，结合动力学和传热学数学模型，推算得到食品颗粒的温度-时间关系和品质变化[15]。在爆炒等食品颗粒为运动状态的热处理工艺中，TTIs法可能是唯一可行的烹饪传热学-动力学分析研究手段[18]。因此有必要构建中式烹饪研究用的TTIs装置。

TTIs装置必须配合数学模型，因此数值模拟是TTIs应用的必要手段。文献[19]建立并验证了TTI指示剂耐高温α-淀粉酶热失活动力学模型，但未结合传热学分析魔芋葡聚糖凝胶载体内部温度与酶活力变化的关系。文献[9-10]分别构建了热质传递数学模型和烹饪动力学模型，文献[17]通过对炒的数值模拟，初步了解了烹饪优化的基本规律，但所选数学模型中的关键参数hfp为推断设定，并未得到试验验证。

本文选用耐高温α-淀粉酶（博立生物）作为指示剂，测定其动力学参数D值、z值；以魔芋凝胶（g-KGM）作为食品模拟物，共同构建了 TTIs。在设定的理想条件下，对构建的TTIs的酶失活动力学模型和传热数学模型进行了验证，证明了其可靠性。同时，应用构建的 TTIs和数值模拟，测定了实际烹饪爆炒过程的表面换热系数[17]，证明了其实用价值。

1 材料与方法

1.1 材 料

魔芋纯化粉（武汉强森公司）；耐高温α-淀粉酶液（原酶液）（江苏博立生物制品有限公司）；玻璃毛细管（上海欣鹏玻璃仪器有限公司），内外径分别为0.8、1.0 mm。

1.2 试 剂

可溶性淀粉，稀碘液，pH值为6的磷酸缓冲液，0.1 mol/L盐酸溶液等。

1.3 仪器、设备及软件

烹饪传热学及动力学数据采集分析系统[20]（自研），温度测定准确度为±0.05 ℃；热电偶（奥崎自动化仪表设备有限公司）；紫外分光光度计（上海欣茂仪器有限公司）；pHS-3C精密-pH计（上海雷兹仪器厂）；超级恒温油浴锅（上海博迅实业有限公司），通过油浴锅的油循环运动形成油对静止的TTIs装置的相对运动，模拟烹饪液体-颗粒加热，装置参见图1。

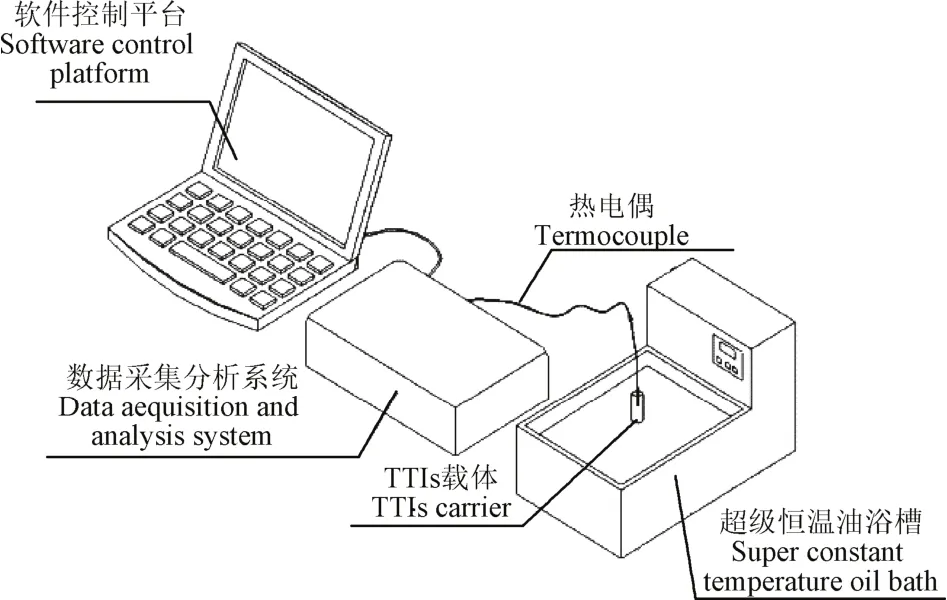
图1 设定条件下时间温度积分器（TTIs）动力学及传热学模型验证装置Fig.1 Time temperature mtegrators (TTIs) kinetics and validation apparatus of heat transfer model under set conditions

1.4 理论、方法及条件

1.4.1 TTIs装置相关原理方法

1）酶的热失活动力学原理根据动力学原理，酶加热失活D值与酶浓度之间的关系为

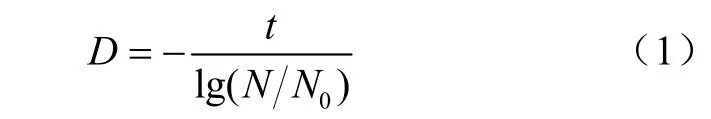
式中D值为在一定温度下酶活力减少90%所需的时间，min；t为加热时间，min；N0为原酶活，U；N为加热时间为t时的剩余酶活，U。

而z值与D值的关系为

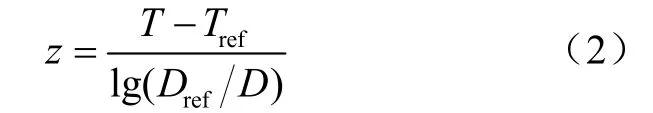
式中z值为D值减少90%所需要的温度，℃，表征酶失活的温度敏感性；T为颗粒中心温度，℃；Tref为参考温度，取100 ℃；Dref为Tref下对应的D值，min。

参考温度下等效加热时间，即在变温加热条件下酶活变化等效于参考温度下的恒温加热时间，可定量表征加热强度，计算公式为

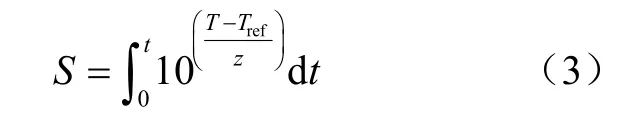
式中S为参考温度下的等效加热时间，min。

2）指示剂酶失活动力学模型构建

由温度-时间关系根据式（3）得到参考温度Tref下等效加热时间S，测得Tref处理不同时间后酶活残存率对数lg(N/N0)与时间(t)的回归方程，将式公式（3）带入得到对应的酶活。积分计算利用Matlab软件完成。

3）原酶活力测定

按文献[19]中耐高温α-淀粉酶酶活测定和计算方法，将原酶液稀释不同倍数，测定稀释液与淀粉液反应不同时间对应的吸光度值（A），并对其对数化(lgA），得到与时间的关系曲线和回归方程；然后测定酶解反应终点时的A值，带入回归方程计算不同稀释倍数的酶反应到达终点所需的时间，由反应终点时间计算出酶活力，求平均值得到平均酶活，即为原酶活力。

4）指示剂毛细管胶囊制备

使用微量注射器将14µL原酶液注入一端封闭的玻璃毛细管（外径1.0 mm，内径0.8 mm），用冰冻处理后的夹具夹住注入原酶液的一端，用酒精喷灯烧结另一端进行密封，制成长度3.10～3.50 cm的毛细管胶囊。

5）原酶液D值、z值的测定计算

将毛细管胶囊经过一定温度-时间处理后，迅速放入冰水混合物中冷却 1 min，用微量注射器将酶液取出至10 mL的容量瓶中，然后用蒸馏水反复冲洗毛细管3次并定容，将酶液稀释714.29倍，按3）中方法测量剩余酶活，按式（1）计算得到D值，按式（2）计算得到z值。

6）魔芋凝胶g-KGM载体的制备

按文献[21]中的方法制备 g-KGM，利用打孔器将凝胶制作成圆柱形。该载体在高温爆炒等条件下不破断、不蒸发，具有很强的烹饪耐受性，适合烹饪研究[21-22]。

7）TTIs装置的构建

按 6）中方法将魔芋凝胶制作成尺寸为Φ0.79 cm× 4.75 cm的圆柱体TTIs载体；将4）中方法制得的毛细管胶囊置入魔芋凝胶载体的几何中心位置，构建成TTIs装置，见图2。

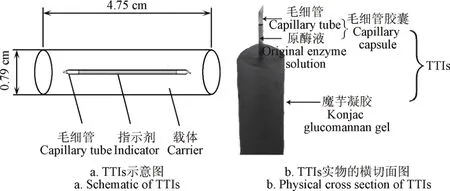
图2 TTIs装置示意图Fig.2 Schematic diagram of TTIs device

1.4.2 液体-颗粒非稳态传热数学模型及数值计算

颗粒为圆柱形TTIs载体或猪里脊肉丝，液体为烹饪用油，假设烹饪开始时颗粒初始温度均匀，油及颗粒热物性稳定，颗粒几何尺寸恒定，忽略毛细管对传热的影响。

1）控制方程

颗粒内部非稳态导热微分方程为

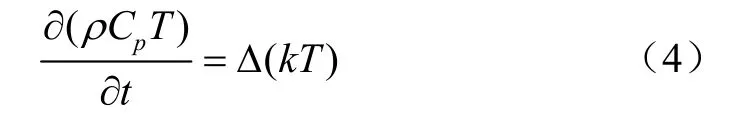
符号意义及单位见表1。

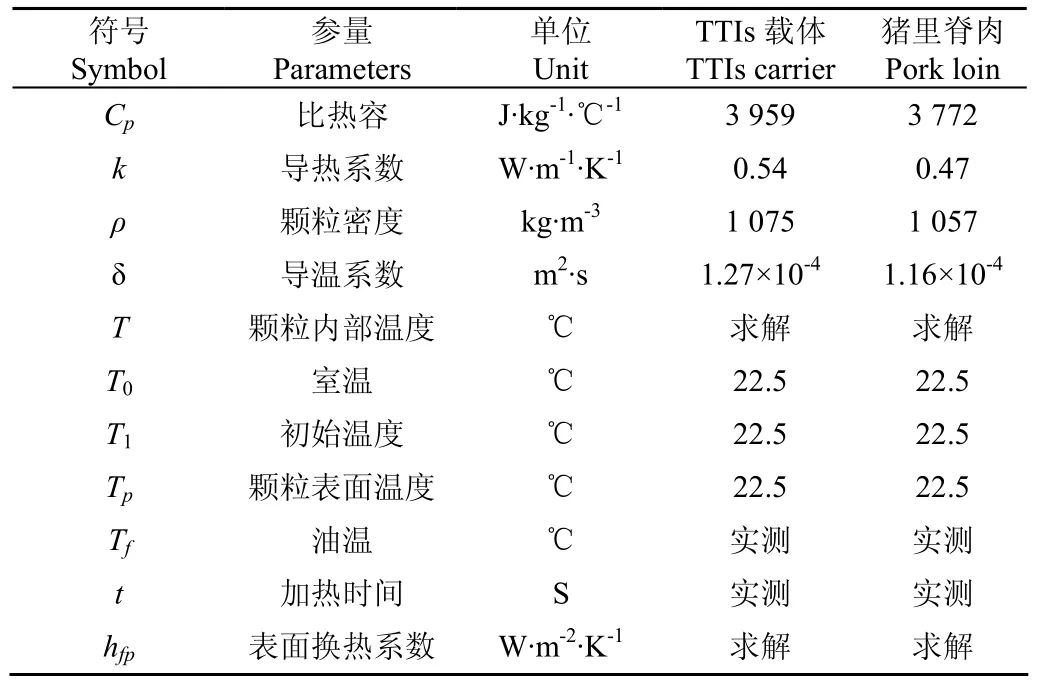
表1 数值计算参数Table1 Mathematical calculation parameters

2）初始条件和边界条件

初始条件：初始温度T1=T0，T0为室温。

边界条件：流体-颗粒对流加热过程中，其边界控制方程为

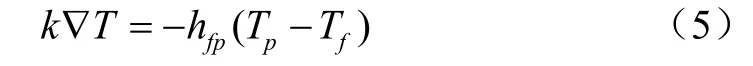
符号意义及单位见表1。

3）网格划分

选取圆柱形载体的1/4建立物理模型，并由ANSYS中的Meshing进行网格划分，网格单元数为317 293，如图3。

图3 网格划分Fig.3 Grid division

4）数值计算方法

利用ANSYS Mechanical对式（4）、（5）进行数值求解。在PREP处理器中定义单元类型、输入热物性参数；在SOLUTION中施加载荷，按表1输入除求解温度T以外的所有参量。若Tf为定值，则直接输入；若Tf变化，则根据实测值利用 Functions Edit线性确定温度-时间变化，通过调用载入器读取。选用JCG自动迭代求解器获得有限元解，并在后处理器中导出中心温度-时间关系。

1.4.3 以最小温度目标总体差平方和法（LSTD）计算hfp

LSTD可反映数值模拟求得温度与实测时间温度的全程差异[23-24]，其计算公式为

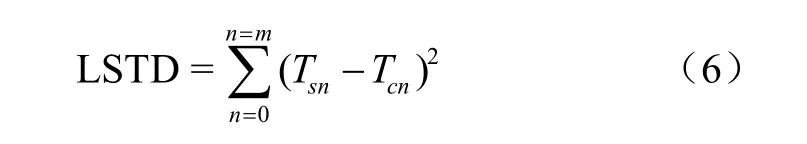
式中LSTD为温度差平方和；Tsn、Tcn分别为在共为m个的第n个时间点分别由数值模拟和采集获得的温度-时间关系。

假设一个hfp，由1.4.2方法得到中心温度-时间关系Tsn-t，针对实测温度-时间关系Tcn计算得到LSTD值。以10 W/(m2·K)为hfp计算步长，分别计算LSTD，得到LSTD最小的hfp。以最小的hfp为计算基准，缩小计算步长到0.1 W/(m2·K)，继续计算LSTD值，得到LSTD最小时相应的hfp即为目标hfp。

1.4.4 设定条件下的TTIs装置准确性验证

1）TTIs载体中心温度-时间关系的实际测量方法

将热电偶插入TTIs载体几何中心位置，利用烹饪传热学及动力学数据采集分析系统采集得到TTIs载体的中心温度-时间关系，设定采集步长为0.1 s，采集时间及温度范围根据试验条件设定。同时测定油温。

2）TTIs装置实际剩余酶活的测定

将TTIs装置在超级恒温油浴锅中加热处理后，迅速取出毛细管胶囊放入冰水混合物中冷却，测定其实际剩余酶活。

3）指示剂酶失活动力学模型验证

在设定条件下，测定 TTIs载体的中心温度-时间关系，按1.4.1方法计算酶活，与TTIs装置实测酶活比较，以证明构建的酶失活动力学模型可靠。

4）与TTIs装置配合的数学模型验证

在设定条件下，由 1.4.2数学模型计算获得的温度-时间关系，按1.4.1方法计算酶活，与TTIs装置实测酶活比较，以证明构建的TTIs装置传热学数学模型可靠。

1.4.5 基于TTIs装置测定爆炒过程hfp

1）爆炒条件

由贵阳新东方烹饪学院一级厨师雷远在该校中餐教学平台上以大火加热操作快速颠锅爆炒。菜籽油与 TTIs装置、猪里脊肉、胡萝卜混合物的质量比约为1:5，TTIs装置和猪里脊肉形状尺寸相同（Φ0.79 cm×4.75 cm）。

2）爆炒过程hfp测定

将TTIs装置和猪里脊肉一起爆炒后，取出TTIs装置中的毛细管胶囊迅速冷却，测定实际剩余酶活。由于爆炒过程存在强烈搅拌，无法实时记录锅内油温变化，参照1.4.4方法每隔10 s采集锅内油温。以0.1 W/(m2·K)为步长，假设一系列hfp，当计算酶活与TTIs实测酶活误差最小时，则认为设定hfp为烹饪中油-猪里脊肉的hfp实际值。

2 结果与分析

2.1 TTIs装置构建及相关原理方法

2.1.1 原酶活力测定

吸光度值的对数lgA与时间t的关系曲线见图4，其对应的回归方程见表2。

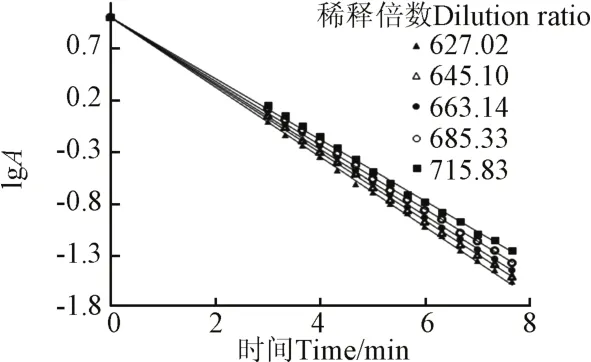
图4 吸光度值的对数与时间关系曲线Fig.4 Relational graph of logarithm of absorbance with time

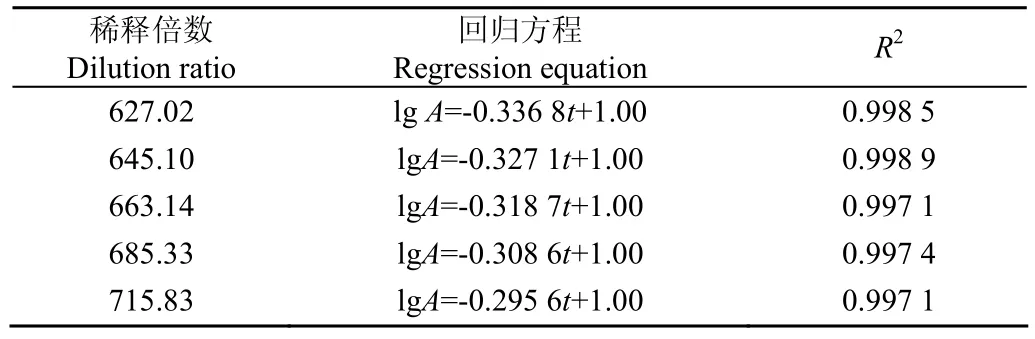
表2 原酶液反应进程回归方程Table2 Regression equation of reaction process of original enzyme solution

按文献[19]方法测得酶解体系反应终点时的吸光度值为0.3，代入表2方程中，分别得到反应终点时间，由反应终点时间计算出酶活力，见表3。对不同倍数稀释液得到的酶活力求平均值，得到平均酶活为55 491.47 U/g，以此作为原酶活力。

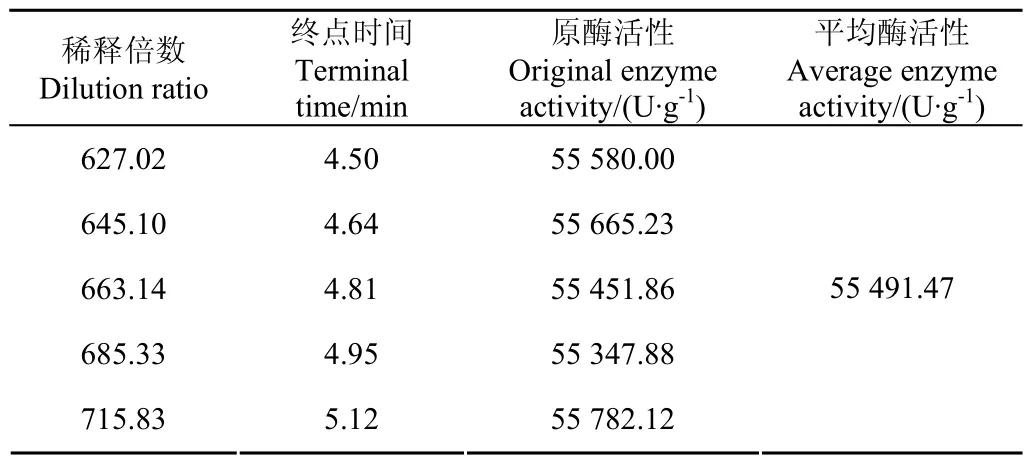
表3 不同稀释倍数下求得的原酶活性Table3 Activity of original enzyme obtained by different concentrations

2.1.2 TTIs指示剂动力学参数D值、z值

酶活残存率与时间关系曲线，结果如图5所示。

图5 不同温度下酶活残存率的对数与时间关系Fig.5 Plot of heating time vs. logarithm of residual activity ratio ofα-amylase at different heating temperatures

根据式（1），由图5中的回归方程得到对应D值。结果见表4。

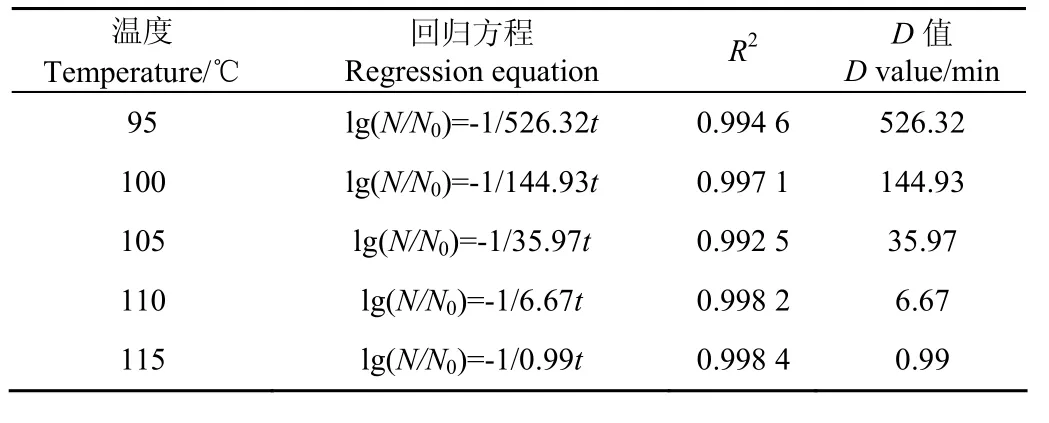
表4 不同温度下原酶液的D值Table4 D values of original enzyme solution at different temperatures

根据式（2），为计算z值，绘制不同温度下原酶液的D值对数曲线，如图6所示。其回归方程为

lgD=−0.135 8T+15.706 (R2=0.993) （7）

将式（7）带入式（2），计算得到原酶液的z值为7.36 ℃。

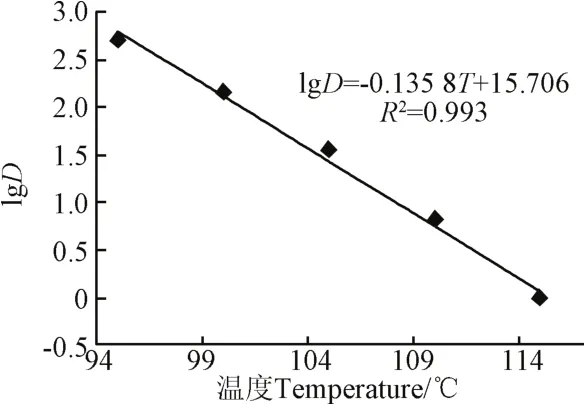
图6 不同温度下原酶液动力学参数D值曲线Fig.6 Dvalue curve of original enzyme solution at different temperatures

2.2 指示剂酶失活动力学模型构建

由1.4.1方法，得到100 ℃分别处理3、11、19、27 min后的剩余酶活，其酶活残存率与等效加热时间S的回归方程为

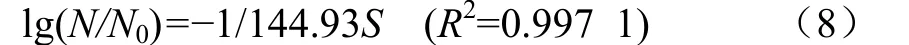
根据式（3）和式（8）由温度-时间关系推算出酶活。

2.3 TTIs装置准确性验证

2.3.1 指示剂酶失活动力学模型的可靠性验证

TTIs实测剩余酶活与酶失活动力学模型推算剩余酶活结果见表5。由表5可知，两者酶活最大误差为2.22%。

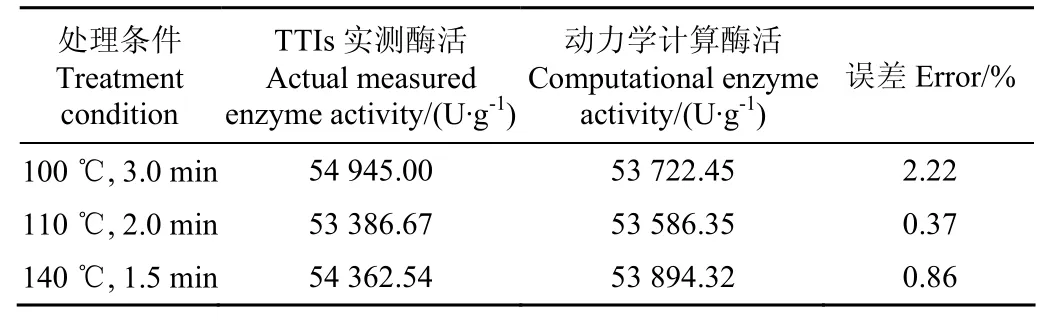
表5 TTIs实测酶活与动力学模型推算酶活Table5 Measured enzyme activity by TTIs and computational enzyme activity by kinetics

2.3.2 设定试验条件下hfp的测算

测定得到hfp见表6。两者温度-时间关系如图7，其相关系数R2分别为0.999 6、0.999 6、0.999 8，平均相对误差δ分别为2.06%、1.48%、0.85%。

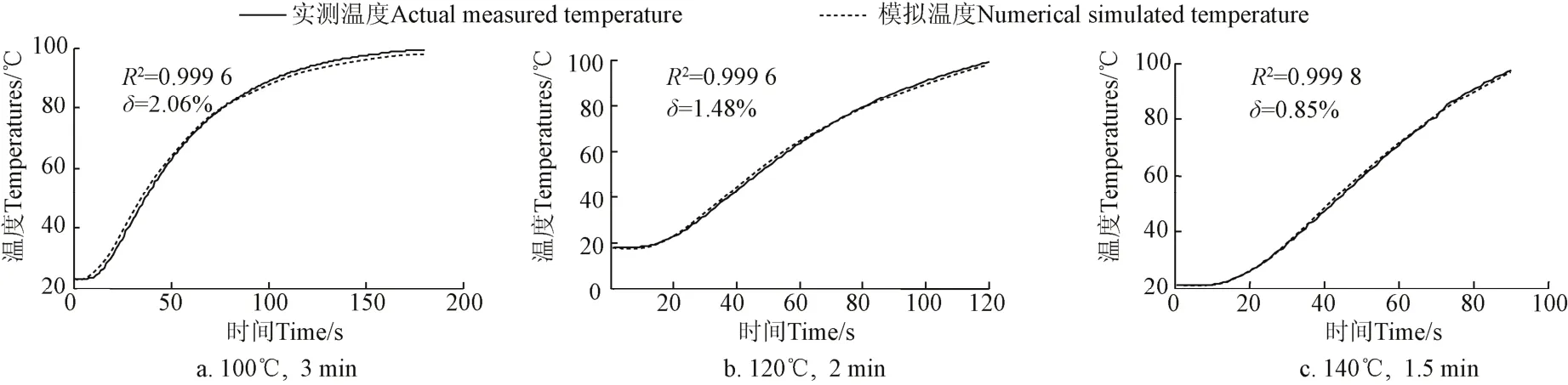
图7 不同加热条件下TTIs载体实测温度与数值模拟温度Fig.7 Actual measured temperature and numerical simulated temperature of TTIs carrier under different heating conditions

2.3.3 TTIs装置传热学数学模型的可靠性验证

按方法1.4.2求解TTIs装置的传热学数学模型，得到中心温度-时间关系，由式（3）、式（8）得到计算酶活，与TTIs装置实测酶活比较见表6。由表6可知，两者酶活最大误差为2.24%。

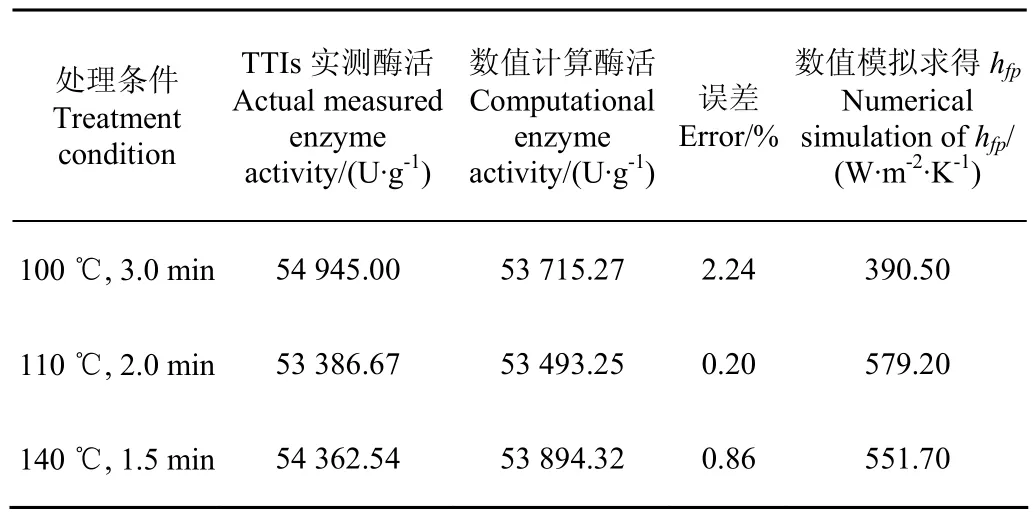
表6 数值计算酶活与TTIs实测酶活Table 6 Enzyme activity by numerical calculation and TTIs

2.4 基于TTIs装置测定爆炒过程hfp

将TTIs装置与猪里脊肉一起爆炒，整个爆炒过程持续50 s，测得油温及TTIs载体的初始温度分别为170、22.5 ℃。爆炒中锅内油温变化结果，见图8。

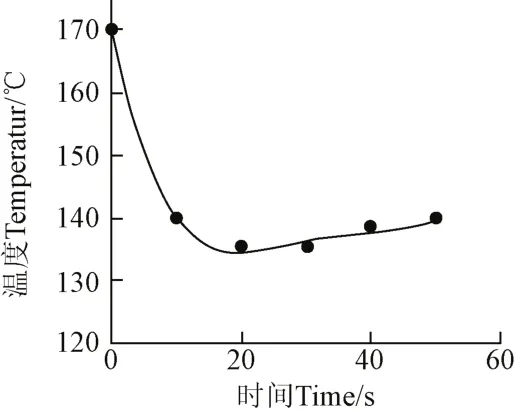
图8 爆炒中锅内油温变化Fig.8 Oil temperature variation in pot during cooking

根据1.4.2中Tf变化条件下的数值计算方法，以图8中的温度数据进行加载，计算得到中心温度-时间关系，结合式（3）、式（8）计算得到剩余酶活-时间关系，见图9。爆炒终点时，由数值计算求得酶活为55 302.95 U/g，与 TTIs装置测得酶活 55 334.85 U/g相比，误差小于0.1%，按1.4.5方法求得hfp为1301.5 W/(m2·K)，误差为0.77%。

图9 实际爆炒过程TTIs装置中心温度及酶活变化Fig.9 Center temperature variation of TTIs in process of stir frying

3 讨 论

3.1 TTIs指示剂的寻找

TTIs指示剂的选用应与热处理的关键品质因子具有相近的动力学参数。爆炒作为中式烹饪的代表性工艺，主要针对肉类、内脏等蛋白质原料，而蛋白质变性的z值为 5～10 ℃[25]。为了寻求到合适的指示剂，本文作者进行了长期努力，先后以辣根过氧化酶、耐高温 α-淀粉酶（杰能科、诺维信）作为指示剂，测得z值分别为55.40[26]、35.34[19]、21.14 ℃[25]，均不能满足爆炒工艺的研究需要。本试验寻找到z值为7.36 ℃的酶源，是烹饪研究的理想指示剂。

3.2 动力学传热学相互印证的理论依据

根据数学物理方程解的唯一性定理[27]，当非稳态传热的边界条件和初始条件一定时，相同热物性物体的温度变化相同。而TTIs指示剂的加热酶活变化仅受温度影响，因此，可用TTIs指示剂的酶活变化动力学结合传热学数学模型推算温度变化，或结合测定的温度变化验证酶活变化动力学模型。当然也可通过数学模型推算 TTIs指示剂的酶活变化。

由 2.3.1可见，由指示剂酶热失活动力学推算的酶活与实测值误差分别为2.22%、0.37%、0.86%，均小于本领域认可的误差5%[19]，证明构建的TTIs指示剂的酶失活动力学模型可靠。由传热学数学模型得到的温度-时间关系计算得到的酶活与实测值误差分别为2.24%、0.20%、0.86%，均小于5%，证明构建的TTIs装置的传热学数学模型可靠。

3.3 魔芋凝胶和猪里脊肉的热物性及形状对结果的影响

魔芋凝胶与真实肉的热物理参数见表1，按1.4.5中烹饪条件处理后，分别得到TTIs装置和里脊肉的中心温度-时间关系，见图10，其相关系数为0.999 7，并分别求得剩余酶活为55 336.02、55 421.01 U/g，与TTIs实际测得酶活55 305.35 U/g的误差分别为0.05%、0.21%，均小于5%。因此，猪里脊肉的热物性对结果的影响误差在允许范围内，魔芋凝胶适合用作猪里脊肉的模拟物。

由2.1.3可知，毛细管胶囊具有一定尺寸，如果载体尺寸很小，影响其试验精度，故本试验所制作的猪里脊肉形状尺寸与TTIs装置相同，为Φ0.79 cm×4.75 cm的圆柱体，与实际爆炒中食品尺寸有一定差别，因此该 TTIs装置的应用具有一定局限性。

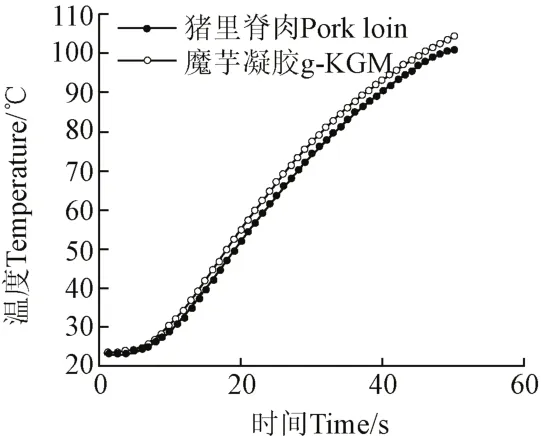
图10 猪里脊肉和魔芋凝胶温度-时间关系Fig.10 Relationship between temperature and time of pork loin and g-KGM

3.4 TTIs在烹饪研究中的应用

对于爆炒等出现剧烈流体-颗粒运动的烹饪过程，要得到其中固体颗粒的温度分布变化及关键参数hfp，是非常困难的。而应用TTIs装置并结合数值模拟技术可以解决这一问题，方法见本文2.4。同时，爆炒是最复杂的烹饪操作，因而该装置经适当改装可以应用于其他烹饪操作的研究。

在文献[28]中，提出了基于 TTIs将手工烹饪转变为自动烹饪程序的方法，中式烹饪研究用TTIs的研制，为该方法提供了技术支撑。

作者在文献[10]中提出了成熟值的概念和公式定义，并实测了一些食品的成熟值[29-30]，但测定成熟值时，需要在食品中插入热电偶，在激烈烹饪中难以实现，而通过TTIs技术，可以方便地测定和推算某一烹饪过程的成熟值，为烹饪研究提供了便利，这方面的研究及应用将随后开展。

4 结 论

寻找到一种动力学参数z值为7.36 ℃的耐高温α-淀粉酶，以其作为指示剂并以魔芋凝胶作为食品模拟物载体，构建了一种适合中式烹饪研究的时间温度积分器（time temperature integrators，TTIs）装置，并对构建的TTIs通过试验进行了酶的热失活动力学与传热学数学模型的相互印证，由指示剂酶热失活动力学推算的酶活与实测值最大误差为2.22%，由传热学数学模型得到的温度-时间关系计算得到的酶活与实测值最大误差为 2.24%。该TTIs可以用于烹饪过程，尤其是激烈烹饪过程的试验传热学研究，并测定表面换热系数为1 301.5 W/(m2·K)，还可以用于将手工烹饪转变为自动烹饪程序，以及用于烹饪成熟值的测定。对其他领域的移动颗粒试验传热学研究具有一定的参考价值。下一步，将研究把指示剂均匀分布于载体中的方法，进而克服毛细管传热形成的误差，提高TTIs的精确度。

[1] Tsironi T, Stamatiou A, Giannoglou, M, et al. Predictive modelling and selection of time temperature integrators for monitoring the shelf life of modified atmosphere packed gilthead seabream fillets[J]. LWT-Food Science and Technology, 2011, 44(4): 1156－1163.

[2] Claeys W L, Van Loey A M, Hendrickx M E. Intrinsic time temperature integrators for heat treatment of milk[J]. Trends in Food Science & Technology, 2002, 13(9): 293－311.

[3] Arias-Mendez A, Vilas C, Alonso A A, et al. Timetemperature integrators as predictive temperature sensors[J]. Food Control, 2014, 44: 258－266.

[4] Guiavarc’h Y P, Dintwa E, Van Loey A M, et al. Validation and use of an enzymic time-temperature integrator to monitor thermal impacts inside a solid/liquid model food[J]. Biotechnology Progress, 2002, 18(5): 1087－1094.

[5] Guiavarc’h Y, Zuber F, Van Loey A, et al. Combined use of two single-component enzymatic time-temperature integrators: Application to industrial continuous rotary processing of canned ravioli[J]. Journal of Food Protection, 2005, 68(2): 375－383.

[6] Tucker G S, Lambourne T, Adams J B, et al. Application of a biochemical time–temperature integrator to estimate pasteurisation values in continuous food processes[J]. Innovative Food Science & Emerging Technologies, 2002, 3(2): 165－174.

[7] Van Loey A, Arthawan A, Hendrickx M, et al. The development and use of an α-amylase based time-temperature integrator to evaluate in-pack pasteurization processes[J]. LWT-Food Science and Technology, 1997, 30(1): 94－100.

[8] de Fazio Aguiar H, Yamashita A S, Gut J A W. Development of enzymic time-temperature integrators with rapid detection for evaluation of continuous HTST pasteurization processes[J]. LWT-Food Science and Technology, 2012, 47(1): 110－116.

[9] 邓力. 中式烹饪热/质传递过程数学模型的构建[J]. 农业工程学报，2013，29(3)：285－292. Deng Li. Construction of mathematical model for heat and mass transfer process of Chinese cooking[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(3): 285－292. (in Chinese with English abstract)

[10] 邓力. 烹饪过程动力学函数、优化模型及火候定义[J]. 农业工程学报，2013，29(4)：278－284. Deng Li. Kinetic functions, optimizing model and definition of “Huohou” for Chinese cooking[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions ofthe CSAE), 2013, 29(4): 278－284. (in Chinese with English abstract)

[11] 邓力，金征宇. 液体-颗粒食品无菌工艺的研究进展[J]. 农业工程学报，2004，20(5)：12－21. Deng Li, Jin Zhengyu. Research advances in aseptic processing of liquid/particle foods[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(5): 12－21. (in Chinese with English abstract)

[12] Cariño-Sarabia A, Vélez-Ruiz J F. Evaluation of convective heat transfer coefficient between fluids and particles in suspension as food model systems for natural convection using two methodologies[J]. Journal of Food Engineering, 2013, 115: 173－181.

[13] Anubhav Pratap Singh, Anika Singh & Hosahalli S. Ramaswamy. Heat transfer phenomena during thermal processing of liquid particulate mixtures: A Review[J]. Food Science and Nutrition, 2015, 57(7): 1350－1364.

[14] Mehauden K, Bakalis S, Cox P W, et al. Use of Time Temperature Integrators for determining process uniformity in agitated vessels[J]. Innovative Food Science and Emerging Technologies, 2008, 9(3): 385－395.

[15] Loey A, Guiavarc'h Y, Claeys W, et al. The Use of Time-temperature Integrators (TTIs) to Validate Thermal Processes[M]. Improving the Thermal Processing of Foods, 2004: 365－384.

[16] Ferruh Erdog˘du. A review on simultaneous determination of thermal diffusivity and heat transfer coefficient[J]. Journal of Food Engineering, 2008, 86(3): 453－459.

[17] 邓力. 炒的烹饪过程数值模拟与优化及其技术特征和参数的分析[J]. 农业工程学报，2013，29(5)：282－292. Deng Li. Numerical simulation, optimization, study of technical features and operational parameters for Chinese cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(5): 282－292. (in Chinese with English abstract)

[18] Tucker G S, Brown H M, Fryer P J, et al. A sterilization Time-Temperature Integrator based on amylase from the hyperthermophilic organism Pyrococcus furiosus[J]. Innovative Food Science and Emerging Technologies, 2007, 8: 63－72.

[19] 王金鹏，徐林，邓力，等. 用耐高温α-淀粉酶构建时间-温度积分器[J]. 食品与生物技术学报，2010，29(5)：641－647. Wang Jinpeng, Xu Lin, Deng Li, et al. Time-temperature indicator based on thermostable alpha-amylase[J]. Journal of Food Science and Biotechnology, 2010, 29(5): 641－647. (in Chinese with English abstract)

[20] 周杰，邓力，闫勇，等. 烹饪传热学及动力学数据采集分析系统的研制[J]. 农业工程学报，2013，29(23)：241－246. Zhou Jie, Deng Li, Yan Yong, et al. Development of system on data acquisition and analysis of heat transfer and kinetics for Chinese cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(23): 241－246. (in Chinese with English abstract)

[21] 高毅，邓力，金征宇. 对魔芋葡甘聚糖凝胶：一种新型食品模拟物的研究[J]. 食品工业科技，2007，28(5)：107－109. Gao Yi, Deng Li, Jin Zhengyu. Konjac glucomannan one kind of new food simulation study[J]. Science and Technology of Food Industry, 2007, 28(5): 107－109. (in Chinese with English abstract)

[22] Wang Jinpeng, Deng Li, Li Yin, et al. Konjac glucomannan as a carrier material for time-temperature integrator[J]. Food Science and Technology International, 2010, 16(2): 127－134.

[23] 李玉振等译. 食品科学手册[M]. 北京：轻工业出版社，1989：282.

[24] Weng Zhijun, Hendrickx M, Maesmsans G. The use of time-temperature-integrator in conjunction with mathematical modelling for determining liquid/particle heat transfer coefficients[J]. Journal of Food Engineering, 1992, 16: 197－214.

[25] 周杰. 中式烹饪 TTIs系统的构建[D]. 贵阳：贵州大学，2013. Zhou Jie. Construction of TTIs System in Chinese Cooking[D]. Guiyang: Guizhou University, 2013. (in Chinese with English abstract)

[26] 高毅. 新型食品模拟系统在流态化固体食品超高温杀菌研究上的应用[D]. 无锡：江南大学，2007. Gao Yi. Application of the New Food Model System in study of Fluidization Solid Foods Ultrahigh Temperature Sterilization Technology[D]. Wuxi: Jiangnan University, 2007. (in Chinese with English abstract)

[27] 梁昆淼. 数学物理方法[M]. 北京：高等教育出版社，2010：122－127.

[28] 邓力. 基于时间温度积分器将手工烹饪转变为自动烹饪的方法[J]. 农业工程学报，2013，29(6)：287－292. Deng Li. Method to convert manual cuisine into automatic operations based on time-temperature integrators[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(6): 287－292. (in Chinese with English abstract)

[29] 闫勇，邓力，何腊平，等. 猪里脊肉烹饪终点成熟值的测定[J]. 农业工程学报，2014，30(12)：284－292. Yan Yong, Deng Li, He Laping, et al. Determination of termination maturity value of the pork loin in cuisine based on the theory of maturity value[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 284－292. (in Chinese with English abstract)

[30] 李文馨. 基于成熟值理论的肉类蔬菜烹饪的动力学研究[D].贵阳：贵州大学，2015. Li Wenxin. Study on the Kinetics of Meat and Vegetables in Cuisine based on the Theory of Maturity Value[D]. Guiyang: Guizhou University, 2015. (in Chinese with English abstract)

Establishment and verification of time-temperature integrators for Chinese cuisine

Deng Li, Huang Delong, Peng Jing, Wang Xiao, Cui Jun, Zeng Xuefeng, He Laping
(School of Liquor and Food Engineering,Guizhou University,Guiyang550025,China)

Chinese cuisine is regarded as a kind of traditional artistry that has multiple genres, various cooking methods and complicated cooking skills. Stir-frying, a typical operation in Chinese cuisine, normally has the characteristics of short time and drastic stirring. Due to the drastic stirring, food particles rapidly move, so common research methods cannot be used to investigate the internal temperature-time relationship of particles in liquid-particle heat transfer process by this operation, such as the thermocouple method and the numerical simulation method, both of which are limited to determine heat transfer coefficient. In order to realize the standardization and automation of Chinese cuisine, it is necessary to master the changing rules of heat transfer and quality during cooking process, and therefore, time-temperature integrators (TTIs) and the corresponding heat transfer - kinetics mathematical model are crucial or even indispensable methods for the researches on quality changes of cooking. The time-temperature integrator, a small equipment composed of an indicator and a carrier, was used to simulate the changes of target quality parameters, time and temperature history as well as food analogues. Therefore, the indicator must have key quality factors that are similar to kinetic parameters in real food materials, and the shape of food analogues must have similar thermal physical properties to real food system. Protein denaturation is widely used to represent quality changes in cooking process. Surprisingly, a kind of thermostableαamylase with the similarzvalue (7.36 ℃) to protein denaturation (5-10 ℃ ) was discovered and successfully applied as an indicator in our experiment. Specifically, the indicator was encapsulated in a capillary tube and then embedded in a carrier with particular shape for establishing TTIs. The carrier was made of konjac glucomannan gel (g-KGM) which has superior heat resisting property. Subsequently, to simulate cooking process of liquid-particle food under the specific heat transfer condition, the changes of enzyme activity were determined by TTIs, and the theoretical temperature-time relationship was calculated with the unsteady heat transfer mathematical model and then compared with practical experimental results. The temperature curve with the minimal gap of theoretical and actual value was obtained on the basis of the least summation of the squared temperature difference for overall target (LSTD). Finally, the residual activity ofαamylase was obtained based on kinetics methods. And the difference with the measured enzyme activity was not more than 2.24%, indicating the TTIs mathematical model was accurate and reliable. Furthermore, the TTIs mathematical model was used to determine the heat transfer coefficient during stir-frying process of Chinese cuisine. The results showed that the TTIs combined with numerical simulation was appropriate for analyzing and measuring heat transfer process, even for the situations conventional heat transfer experiment method was powerless or some other stormy cooking process with liquid-particle. In addition, armed with quality change kinetics, the heat transfer could be analyzed especially for heated treatment of liquid-particle. That is to say, this method may provide key technology for procedure analysis and process optimization of Chinese cuisine. Moreover, it can also be applied to those studies on actual heat transfer process of moving particles in other field.

heat transfer; temperature; enzymes; Chinese cuisine; time-temperature integrators (TTIs); temperature-time relationship; surface heat transfer coefficient

10.11975/j.issn.1002-6819.2017.07.037

TS201.1

A

1002-6819(2017)-07-0281-08

2016-08-22

2017-04-11

国家自然科学基金项目（31660449）；贵州省科技计划项目（黔科合农G字[2013]4016号）；贵州省重大科技专项计划项目（黔科合重大专项字[2015]6004）；贵阳市科学计划项目（生物重大专项[2010]筑农合同字第8-1号）

邓 力，男，江苏南京人，教授，博士，主要研究方向为自动烹饪、复杂食品加工过程的数值分析、现代杀菌技术及挤压技术。贵阳 贵州大学酿酒与食品工程学院，550025。

Email：denglifood@sohu.com