基于GAMIT/GLOBK的卫星定轨研究

曹炳强,许长辉,成英燕,余新平,逄晓东,李宇博

(1.中国测绘科学研究院,北京 100830;2.山东科技大学,山东 青岛 266000; 3.青岛市勘察测绘研究院,山东 青岛 266000)



基于GAMIT/GLOBK的卫星定轨研究

曹炳强1,许长辉1,成英燕1,余新平2,逄晓东3,李宇博3

(1.中国测绘科学研究院,北京 100830;2.山东科技大学,山东 青岛 266000; 3.青岛市勘察测绘研究院,山东 青岛 266000)

本文介绍了GAMIT/GLOBK软件在卫星定轨中的应用,详细介绍了GAMIT/GLOBK定轨的参数设置以及步骤,然后分别以广播星历作为初始轨道信息进行了全球和区域的定轨,最后将全球解和区域解进行了叠加定轨。并分别对其定轨精度进行了进一步的统计分析。

IGS;全球解;区域解;叠加定轨;精度

0 引 言

全球卫星导航系统(GNSS)导航星座的定轨结果能够影响到导航卫星的定位应用精度。我国目前正在进行新一代卫星导航定位系统的组网工作,借鉴国际GNSS服务(IGS)的经验,建立自己的分析中心,利用全球观测数据进行轨道的精化,提供高精度领域的应用[1-3]。目前国际上比较出名的数据处理软件,如GAMIT/GLOBK,BERNESE和PANDA都可以用来进行定轨,国内外的学者基于这几种软件也进行了大量研究,并得出了许多有益结论,但是对于全球网和区域网叠加定轨的研究很少,尤其在进行叠加定轨时,对全球解的IGS站的选择及数量的多少研究很少[4-5]。

目前全球共有300多个IGS站,这些台站在各个地区的数量及分布密度是不一样的,如何合理有效地选择出稳定分布均匀的台站来进行卫星的定轨显得尤为重要[6]。本文,首先简单介绍了进行GAMIT/GLOBK定轨的方法流程以及如何快速有效的选出精度高的IGS站,然后分别进行了全球解和区域解定轨,最后将全球解与区域解进行了联合定轨,并分别对其定轨精度进行了进一步的分析。

1 数据处理

1.1 定轨原理

卫星定轨的基本原理为:首先利用给定的卫星轨道初值以及力学模型的近似值,利用合适的积分方法求得卫星运动方程、卫星的位置、速度向量、以及对卫星轨道初值和力模型参数的偏导数。然后通过建立线性观测方程精确的卫星轨道初值、力模型参数和其它待估参数。最后利用求解出的卫星轨道初值和力学模型参数对卫星运动方程进行积分,得到精确的卫星轨道[7]。

1.2 处理方法

GPS定轨采用的是从定轨日的中心弧段时刻的轨道参数向两边积分的方法,一般为单天积分、3天积分、5天积分以及7天积分等,本文主要计算了单天解、三天解以及七天解。

单天解的解算在进行单天轨道改进时,直接将单天计算结果生成的T文件由ttongs程序转换为sp3格式的地固系星历文件,然后运行orbdif模块,与当天的精密星历比较,得到GPS定轨的外符合精度文件。

多天解的解算是利用多日轨道弧段的叠加来获取较高精度的常用方法。距离中心弧段越远,定轨精度越低。三天解为例子,一般对于由连续3天的观测资料确定中间一天的卫星轨道的做为[8-9]:

1) 广播星历获得先验轨道信息,对于其他两天弧段的估计都以计算中间一天获得的轨道参数作为基础;

2) 将单天生成的h文件通过GAMIT/GLOBK的平差模块进行轨道综合,生成平差结果的org文件;

3) 执行glbtog脚本命令生成一个新的g文件;

4) 新的g文件代入中间一天,通过ARC模块对g文件进行一次积分生成T文件;

5) 同上单天解的方法。这样就可以获得较为精确的卫星轨道。

1.3 处理策略

本次计算所采用的软件为GAMIT10.50,采用RELAX解,解的数据类型为LC-HELP,卫星截止高度角为10°,每2 h设置一个对流层延迟参数,对基准站和卫星轨道分别进行强约束和松弛约束,对基准站坐标X、Y、Z方向的约束为5 mm、5 mm、10 mm.采用BERN光压模型,J2000惯性系,ARC参考系统为IGS92[10].

2 基准站的选择

全球共有300多个IGS站,首先要进行IGS站的选择。按照连续性原则、稳定性原则、高精度原则、多种解原则、平衡性原则和精度一致性原则6个方面对台站进行选择。首先利用站点的时序等资料按照一定标准对各台站的数据质量进行分析,并对测站进行初步的筛选。然后使用七参数法站点进行精选,发现这样选择的站点在局部地区(例如欧洲地区)分布仍然很密集。因而又对精选的测站进行了监督分类,使其在全球的分布符合均匀化的原则[11]。选完之后的测站分布如图1所示。

3 定轨算例

本次计算的数据为2009年,年积日181～187共计七天的观测数据。选用的IGS站如图2所示。

3.1 区域站定轨

算例一：利用中国区域内的7个IGS站进行单天弧长的轨道改进计算。定轨结果如图3所示。

算例二：中国区域内的7个IGS站进行三天弧长的轨道改进计算,定轨结果如图4所示。

算例三：利用中国区域内的7个IGS站进行七天弧长的轨道改进计算,定轨结果如图5和表1所示。

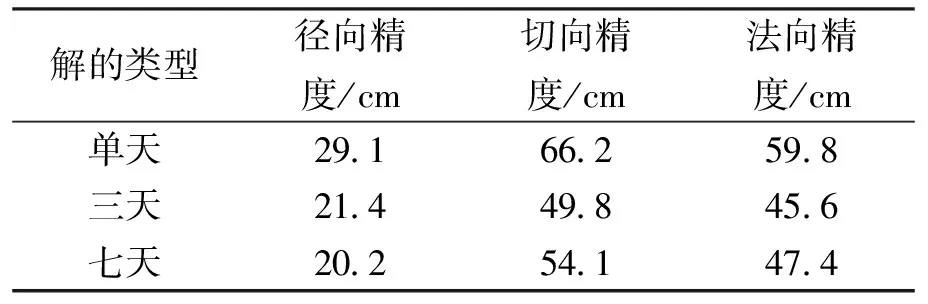
表1 定轨精度对比

由上可以得出,在进行区域定轨时,多天解的精度明显高于单天解的精度。这是由于进行多天轨道法方程合并的时候,相当于增加了卫星弧段的观测值,卫星约束条件增强,这样可以得到中间一天的精度较高的轨道。其中三天解的综合定轨精度要高于七天解的精度,原因是七天的初始轨道是合并的七天的广播星历,这样导致了卫星的轨道弧线增长,因而星历精度降低,致使最终定轨结果精度略差于三天解;其中卫星径向的精度要明显高于切向和法线的精度,原因是径向的受力更容易用模型模拟。

3.2 全球站定轨

算例一：利用全球范围内的90个IGS站进行三天弧长的轨道改进计算,定轨结果如图6所示。

算例二：为研究测站数量对于定轨精度的影响,对上述的90个IGS站进行了均匀分布化处理,得到了45个IGS站,如图7所示。利用 45个IGS站进行三天弧长的轨道改进计算,定轨结果如图8所示，定轨精度所表2所示。

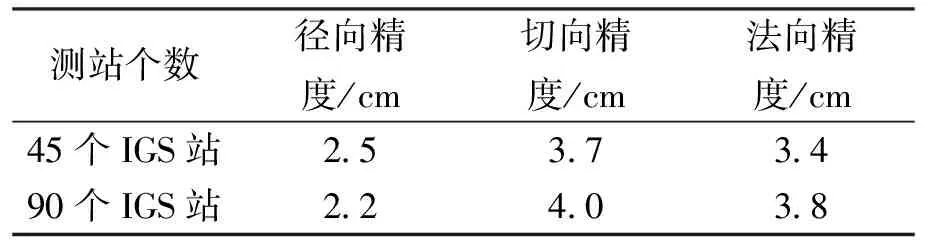
表2 全球范围内定轨精度对比

由表2可以看出,增加了IGS站的数量及分布范围,卫星轨道在径向、切向和法向方向的精度较区域解都有很大改善。当同时用全球分布的测站进行定轨时,90个基准站的定轨精度在径向上高于45个基准站的结果,但是在其他两个方向的定轨结果都要低于45个基准站的结果。而且在用90个基准站进行解算时,解算效率也变很低,所以综合来说,在进行定轨时如何选取适当数量和合理地理分布的基准站显得尤为重要。对于我国的第二代北斗导航卫星系统来说,增加定轨基准站的区域数量以及扩大基准站的全球分布范围是提高其定轨精度的关键。

3.3 叠加定轨

将183～185天的全球站和区域站的观测数据进行了独立解算,然后利用globk进行全球45个IGS站解和区域解的联合平差,具体步骤如下:

1) 首先将两种解的H文件利用GLOBK的htoglb模块将其转换为二进制文件;

2) 将转换为二进制的*.glx文件做一个列表文件,然后将同一天的*.glx文件后面加“+”,需要注意的是每一天的最后一个*.glx不用加“+”;

3) 修改控制文件,将控制文件globk-comb.cmd中的“out-glb H-SCAL.GLX”命令行打开;

4) 执行glred合并:“glred 6 glred.prt glred.log *.gdl globk-comb.cmd”,得到每天1个的全球二进制H文件;

5) 执行globk平差,注意进行定轨时一定要进行卡尔曼反向滤波,“globk 6 globk.prt globk.log *gdl globk-comb.cmd”,得到org文件。

然后从求解得到的org文件中提取出轨道信息。联合定轨的测站分布以及定轨结果如图9所示,图10所示，定轨精度如表3所示。

表3 不同区域定轨精度对比

从图中可以看到,对于全球解而言,进行全球和区域联合定轨之后,卫星在径向的精度有了2 mm的提高,但是在切向和法向上,因为某些卫星精度比较差,导致卫星的平均精度都要比全球解低。原因可能是在进行联合定轨时,测站在局部密度比较大,观测值的分布不均匀,使法方程求得的部分卫星轨道信息在整个弧段上并不是最优的。对于区域解而言,进行全球和区域联合定轨之后,卫星在每个方向上的精度都有了大幅度的提高,尤其在切向和法向上的精度提高了46.8 cm与41.9 cm.总体来说,因为利用了全球的基准站,所有的卫星弧段都可以被跟踪,所以联合全球IGS站解进行区域定轨,大大增加了区域定轨的精度。

4 结束语

详细介绍了GAMIT/GLOBK的定轨流程,并利用GAMIT/GLOBK软件做了几个定轨实例,可以得出的几点结论:在进行区域定轨时,多天解可以提高定轨的精度,其中三天解的轨道精度最好;在进行全球IGS站定轨时,因为所有的卫星都可以被跟踪,所以全球范围内的基准站定轨精度比区域基准站定轨的精度有较大的提高,但是随着测站数量的增加,精度改善不明显;进行全球与区域联合定轨时,全球解对于区域定轨的精度提高有很大的改善。

[1] Herring T A、KING R W、MCLUSKYl S C.GAMIT reference manual,release 10.35[R].Massachusetts Institute of Technology at Australia Nationnal University, 2009:78-83.

[2] 姚宜斌. GPS精密定位定轨后处理[M].北京:测绘出版社,2008:72-75.

[3] 李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995:45-47.

[4] 陈慧杰，杜瑞林，赵齐乐，等.关于区域定轨对于全球定轨的的研究[J].大地测量与地球动力学,2011,31(6):85-89.

[5] 周善石，胡小工，吴斌.区域监测网精密定轨与轨道预报精度分析[J].中国科学:物理学力学天文学,2010,40(6):800-808

[6] 张睿.基于地面基准站观测技术的GPS卫星定轨研究及程序设计[D].西安:长安大学,2013:35-48.

[7] 王武星，顾国华.利用基准站观测资料确定GPS卫星轨道[J].大地测量与地球动力学,2003,23(3):112-115.

[8] 秘金钟，党亚民，蒋志浩，等.基于国家测绘局GPS连续运行参考站的定轨[J].辽宁工程大学学报(自然科学版), 2009,28(2):202-205.

[9] 任锴，贾小琳，宋小勇.Gamit定轨软件分析[C]//第二届中国卫星导航学术年会,2011:1-4.

[10] 曹炳强，成英燕，许长辉.海潮模型对连续跟踪参考站数据解算的影响[J].测绘科学,2015,40(12):108-111.

[11] 高乐，成英燕，郑作亚，等.GNSS数据处理框架点的选取方法研究[J].大地测量与地球动力学, 2011,31(2):133-136.

Research of Orbit Determination Based on GAMIT/GLOBK

CAO Bingqiang1,XU Changhui1,CHENG Yingyan1,YU Xinping2,PANG Xiaodong3,LI Yubo3

(1.ChineseacademyofSurveyingand,Mapping,Beijing100830,China; 2.ShandongUniversityofScienceandTechnology,Qingdao266000,China; 3.QingdaosurveyingandMappingInstitute,Qingdao266000,China)

This paper introduces the application of GAMIT/GLOBK in satellite orbit determination,the parameter setting and the steps of GAMIT/GLOBK orbit determination are introduced in detail. Then the global and regional orbit determination is carried out based on the broadcast ephemeris as initial orbit information. And the accuracy of the orbit determination is analyzed further.

IGS; Global solution; regional solution; superposition of orbit determination; precision

10.13442/j.gnss.1008-9268.2017.01.016

2016-06-20

国家自然科学基金(批准号：41374014); 国家基础测绘科技项目(编号：2016KJ0205); 国家公益性行业专项(编号：B1503)； 国家重点研发计划(编号：2016YFB0501405)

P228.4

A

1008-9268(2017)01-0077-05

曹炳强 (1990-),男,硕士生,主要从事GPS数据处理及多系统卫星定轨研究。

许长辉 (1981-),男,副研究员, 主要从事GNSS精密单点定位研究。

成英燕 (1965-),女,研究员,主要从事参考框架维持与更新研究。

余新平 (1992-),男,硕士生,主要从事时间序列的研究。

联系人： 曹炳强 E-mail: 1182609094@qq.com