连通图平均距离的界
2017-05-15郝国亮谢智红张家骥
郝国亮, 谢智红, 张家骥
(东华理工大学 理学院, 江西 南昌 330013)
在分析传输网络的性能与效率时, 有两个特别受关注的因素, 即最大传输时延与平均传输时延, 在图论中它们常被近似地抽象为两个图参数, 即直径与平均距离。 这两个图参数在结构化学、建筑学、通讯网络等领域有着重要的应用。设G=(V(G),E(G))是一个无向简单图, 其中V(G)为顶点集,E(G)为边集。对G的顶点u和v, 若存在一条u-v路, 则称u和v是连通的。 若G中的任意一对顶点都是连通的, 则称G为连通图。G中最短u-v路的长称为u和v的距离, 记为d(u,v)=dG(u,v)。对于u∈V(G), 顶点u的离径定义为ecc(u)=eccG(u)=max{d(u,x)∶x∈V(G)}。最小离径称为半径, 记为r(G);最大离径称为直径, 记为d(G)。若删掉连通图G中顶点μ所得图是非连通图,则称μ是G的割点。不含割点的连通图称为块。 用deg(u)表示顶点u在图G中的度。
图G的σ(u)指标定义为
σ(u)=σG(u)=∑x∈V(G)d(u,x)
记n阶连通图G中任两点间(无序对)距离和与平均距离分别为


在关于图的距离和平均距离研究方面, Chung(1998)建立了平均距离与独立数之间的相互关系。 周涛等(2004)利用构造分析方法给出了Ore 定理的一个简单证明。 卢永红等(2013)得到了两类特殊树的平均距离的精确值。相关研究还可以参阅卢永红等(2010)、Dankelmann(2000)、Doyle(1977)、Dankelman等(2004)、Plesnik(1984)文献。
本文主要利用图G的σ(u)指标得到了与顶点数、边数、直径和半径相关的连通图的平均距离的上下界。
1 平均距离的上界
引理1 若G是顶点数为n的连通图,则对任意顶点u∈V(G),



(1+2+…+k)+(n-k-1)k=
f(k)≤f(d(G))=
证毕。
由引理1可得图的平均距离的上界:
定理1 若G是顶点数为n的连通图,则

证明 由引理1可得

证毕。
2 平均距离的下界
引理2 若G是顶点数为n的连通图,则对任意顶点u∈V(G),
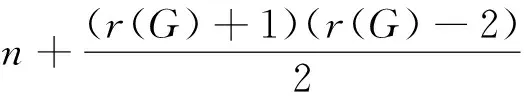
证明 对任意顶点u∈V(G),设ecc(u)=k且P=uu1u2…uk是G的一条路使得d(u,uk)=k。则G中剩余顶点不妨记为uk+1,uk+2,…,un-1。注意d(u,ui)=i(1≤i≤k)且d(u,ui)≥1(k+1≤i≤n-1),因此

(1+2+…+k)+(n-k-1)=

证毕。
由引理2可得如下结论:
定理2 若G是顶点数为n的连通图,则

证明 由引理2可得

证毕。
引理3 设G是顶点数为n的块且r(G)≥2,则对任意顶点u∈V(G),
σ(u)≥2(n-1)-deg(u)+(r(G)-2)2
证明 对任意顶点u∈V(G),设ecc(u)=k,并设i为图G中与u的距离为i的顶点数(i=1,2,…,k)。 由于G是块, 所以1≥2(i=1,2,…,k-1)且k≥1。 因此, 要使
σ(u)=1·1+2·2+…+k·k
n-1-deg(u)-2(k-3)-1=
n-deg(u)-2k+4。
于是
σ(u)=1·1+2·2+(3·3+4·4+
…+(k-1)·k-1)+k·k≥
deg(u)+2(n-deg(u)-2k+4)+
2(3+4+…+(k-1))+k·1=
2(n-1)-deg(u)+(k-2)2≥
2(n-1)-deg(u)+(r(G)-2)2
证毕。
定理3 若G是顶点数为n,边数为m的块且r(G)≥2,则

证明 由引理3及握手定理可得

证毕。
卢永红,康淑瑰,孟献青. 2013. 两类特殊树的距离和及平均距离[J]. 中北大学学报:自然科学版, 34(5): 496-499.
卢永红,刘宏英. 2010. 几类树的距离和及平均距离[J].山西师范大学学报:自然科学版,24(2):16-19.
周涛,徐俊明,刘隽. 2004. 图直径与平均距离的极值问题研究[J].中国科学技术大学学报, 34(4):410-413.
Chung F R K. 1988. The average distance and the independence number[J]. Journal of Graph theory, 12: 229-235.
Dankelmann P. 2000. Entringer R. Average distance, minimum degree, and spanning trees[J]. Journal of Graph Theory, 33(1):1-13.
Dankelmann P, Oellermann O R, Wu J L. 2004. Minimum average distance of strong orientations of graphs[J]. Discrete Applied Mathematics,143:204-212.
Doyle J K. 1977. Mean distance in a graph[J]. Discrete Math., 17:147-154.
Plesnik J. 1984. On the sum of all distances in a graph or digraph[J]. J. Graph Theory, 8:1-21.
