自适应递阶遗传神经网络测井岩性识别方法研究

温志平，方江雄,2,3，刘 军，郑成龙

(1．东华理工大学 地球物理与测控技术学院，江西 南昌 330013；2．核技术应用教育部工程研究中心，江西 南昌 330013；3．流域生态与地理环境监测国家测绘地理信息局重点实验室，江西 南昌 330013 )

岩性识别作为储层评价、油藏描述和求解储层参数的一种重要手段，准确的岩性识别结果是地质勘探和开发的有效依据。但在实际地质条件中，由于储层介质的不均匀性和测井参数的非线性性，导致传统的岩性识别方法识别率较低，无法准确的揭示储层的真实特性，比如交会图法、数学概率统计法和聚类分析法(Juprasert et al.,1980;程国建等，2007;王祝文等，2009)。BP神经网络由于具有良好的非线性特征，灵活而有效地学习方式，对非线性系统具有很强的模拟能力，被运用于地球物理测井岩性识别领域(Simon et al.,2009；张治国，2006；高美娟，2005)。然而，这些BP神经网络采用梯度下降法进行参数寻优，导致非凸能量泛函易陷入局部最小值，并且无法自适应地选择学习率和网络结构(Sutton, 1986)。遗传算法由于具有概率性全局优化搜索能力，被运用于优化BP神经网络的权值和阈值，从而改善陷入局部最小的机率(Whitley,1995)。但常用的遗传算法只对神经网络的权阈值进行优化，对神经网络拓扑结构优化尚无系统研究，且在遗传操作中交叉变异概率采用固定值，无法准确反映真实的进化过程。Ke等(1998)提出了递阶遗传算法。

针对上述网络结构优化和交叉变异算子取值问题，本文提出自适应递阶遗传算法。该方法主要研究两个方面的内容：①采用层次递进的染色体编码方式对神经网络结构和权阈值进行编码，经遗传进化获取最优染色体，解码后即为最优的网络拓扑结构和网络权阈值；②改进遗传算法中的交叉变异算子，使其依据适应度值和进化阶段发生自适应变化，让遗传算法在保持种群多样性的同时，也能有效加快遗传进化速度和避免“早熟”现象的发生。

递阶遗传算法中交叉概率和变异概率的确定将直接影响算法的收敛性，当交叉概率增大时，种群的多样性加强，但过大的交叉概率使得种群内适应度高的个体以较大的概率被淘汰；当交叉概率减小时，种群内最优适应度的搜索过程减慢，搜索进程陷入局部的可能增加。相似的，当变异概率减小时，种群的多样性降低；变异概率增大时，算法的搜索过程将趋近随机搜索，失去了算法意义。如何确定合适的交叉概率和变异概率是一个难题。自适应的交叉和变异算子可以在遗传进化的不同阶段发生自适应变化，较好的解决了这个问题。

1 自适应递阶遗传神经网络

1.1 BP神经网络

BP神经网络由输入层、隐藏层及输出层组成，经典的三层BP神经网络结构实现了m维到n维的映射，其中m,n∈N+。

BP神经网络的训练过程由信号的正向传播和误差的反向传播两部分构成，输入信号从输入层进入网络，经过隐藏层的加权求和以及函数运算处理后，到输出层输出，这一过程称为信号的正向传播。当输出信号与期望输出存在误差时，将误差信号反馈回网络中，根据BP网络的自适应能力修改网络各层连接权阈值，从而使误差信号变小，这一过程称为误差的反向传播。当误差达到所需精度或达到最大迭代次数时，训练结束，得到最优的网络模型。

1.2 递阶遗传算法

递阶遗传算法引进染色体阶次递进的概念，递阶遗传染色体由控制基因串(CGs)和参数基因串(PGs)两部分构成。控制基因串可为多层设计，其上层控制基因控制管理着下层的控制基因，下层控制基因决定着参数基因的激活或冻结。

控制基因串(CGs)使用二进制1和0表示，其中1表示其下层的基因处于激活状态，0表示其下层的基因处于冻结状态。参数基因串(PGs)由需优化的参数组成，并采用实数进行编码，图1显示了递阶遗传中基因的阶次递进关系。

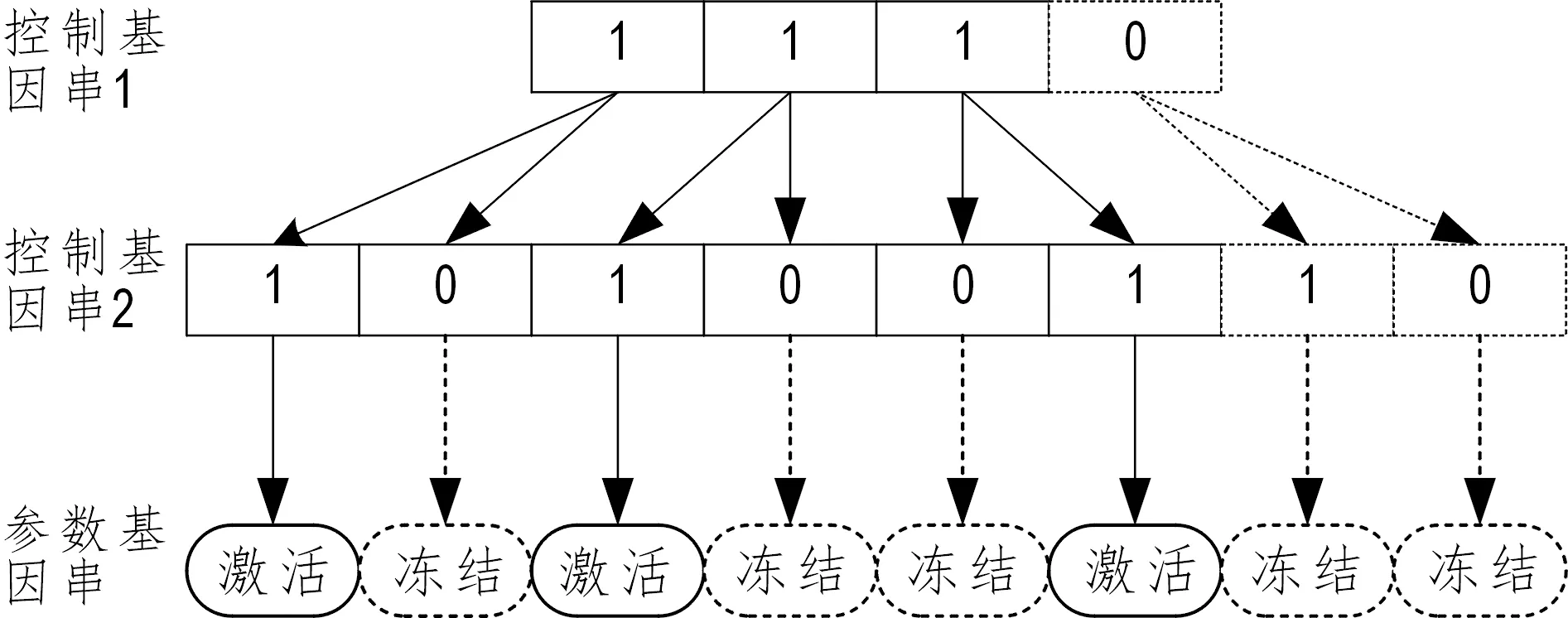
图1 递阶遗传基因的阶次递进关系Fig.1 Order progression relation of hierarchical genetic gene

在神经网络的网络结构中，隐藏层层数、隐藏神经元个数和层间神经元传递参数(网络权阈值)的设计具有明显的阶次递进关系。隐藏决定着隐层神经元是否存在，而神经元决定着神经元之间连接权阈值是否存在。神经网络结构中隐层数及隐层神经元数可由递阶遗传算法中染色体的双层控制基因串(层控制基因CGs1和神经元控制基因CGs2)编码表示，网络中的连接权值和阈值可由参数基因串(PGs)编码表示。

2 AHGA-BPNN岩性识别模型

自适应递阶遗传神经网络(AHGA-BPNN)岩性识别模型，由BP神经网络设计和自适应递阶遗传算法设计两部分构成。其中，BP神经网络设计包括网络初始化、输入信号正向传播、误差反向传播和网络权阈值更新等过程；自适应递阶遗传算法设计包括递阶遗传染色体编码、适应度函数设计、遗传操作算子设计和适应度评价等步骤。

2.1 BP神经网络设计

BP神经网络计算过程包括：网络参数初始化、信号正向传播和误差反向传播过程。其中初始化参数主要包括：输入测井参数和输出岩性类别、网络最大隐藏层层数、隐藏层最大神经元数目、网络最大迭代次数、网络误差精度等；测井曲线数据经预处理后输入网络进行正向传播，经各层函数计算，直至输出层输出，比较实际输出与期望输出，若存在误差，则将误差信号反向传播回网络，网络各层间权阈值实时更新，直至网络输出达到预设精度，网络训练结束。其中网络权阈值更新方式不再采用梯度下降法寻优，而是采用改进的自适应递阶遗传算法进化迭代寻优。

2.2 自适应递阶遗传算法设计

2.2.1 递阶遗传染色体编码

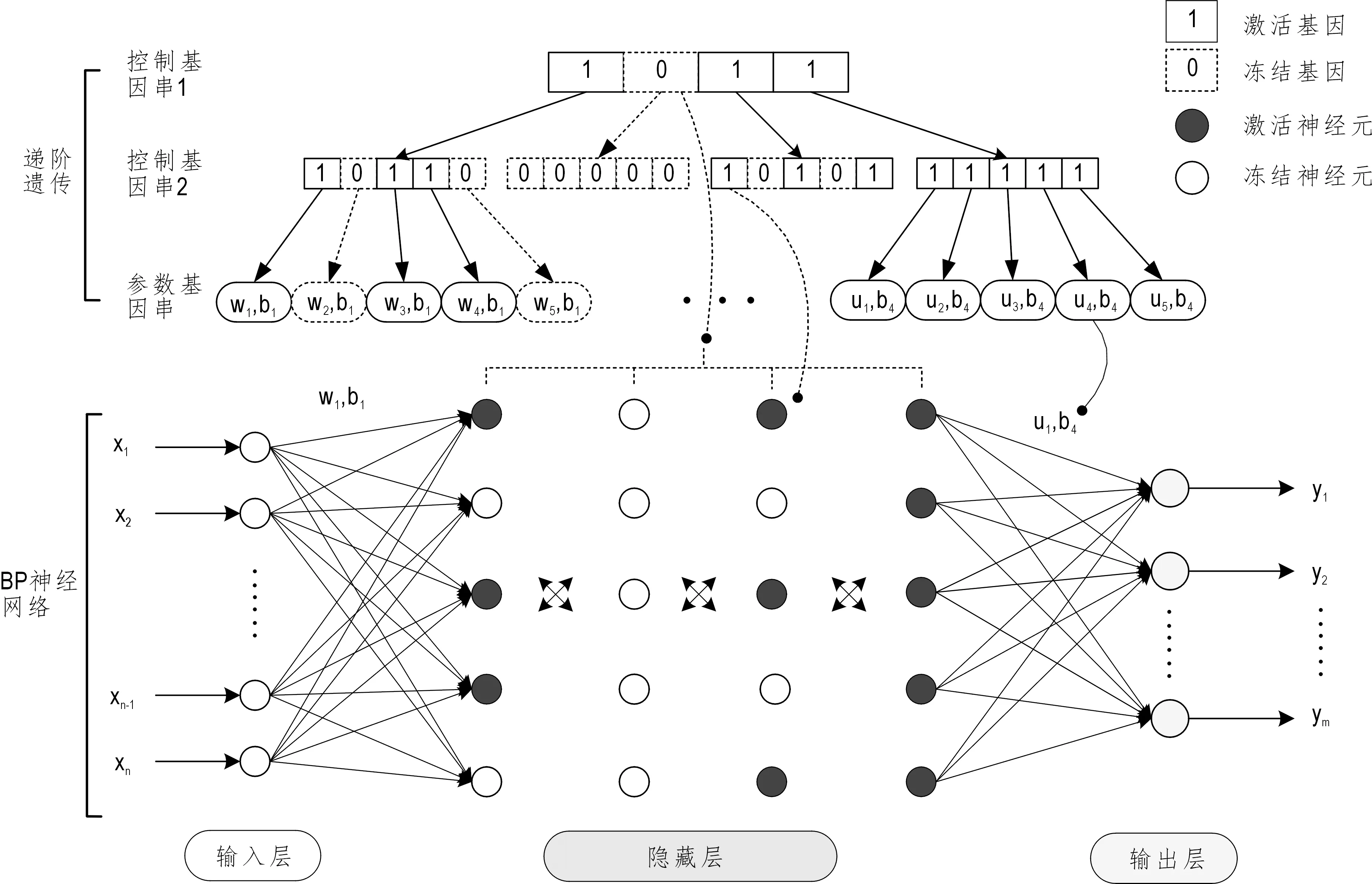
图2 递阶遗传优化BP神经网络权阈值及网络结构示意图Fig.2 Schematic diagram of Hierarchical genetic algorithm optimization weight,threshold and the structure of Back-Propagation neural network

在递阶遗传中，染色体由控制基因和参数基因组成，控制基因均以二进制形式随机生成0、1编码，1表示激活，0表示冻结。在递阶遗传优化BP神经网络中(图2)，层控制基因中的1表示该层被激活，神经元控制基因中的1表示该神经元被激活。参数基因的编码对象为神经网络各层间的权阈值，数据量较大，用实数形式编码。递阶遗传以编码后的染色体进行繁殖进化，当出现最优解，或达到训练代数与停止准则时，第一层控制基因串中1的个数即代表最佳隐藏层层数，第二层控制基因中串的1的个数即代表对应隐藏层中的最佳神经元个数，参数基因串中1的个数即代表前后层对应神经元间权阈值个数。

递阶遗传染色体基因编码时，一条完整的染色体的前部分由控制基因串，后部分由参数基因串组成。控制基因串的长度(CGsL)=隐层数×隐层神经元数。参数基因串的长度(PGsL)=输入层神经元×第一个隐层神经元个数+隐层层数×隐层神经元个数+输出层×最后一个隐层神经元个数+输出层神经元个数。

2.2.2 适应度函数设计

适应度函数是评价神经网络权阈值的一个关键指标，其函数的大小直接关系到遗传算法对神经网络的优化效果。常用网络输出总误差的倒数作为适应度函数：

(1)

式中，m为网络输入层神经元数，yk为网络实际输出，dk为网络期望输出。

但式(1)的适应度值只能反映网络输出误差的大小，缺乏对网络拓扑结构好坏的评价。为解决这个问题，本文将网络复杂度引入到适应度函数设计中，使适应度函数不仅反映网络输出误差的大小，并且体现着神经网络的结构信息，其适应度评价函数如下：

(2)

式中，l为隐藏层神经元数，n为网络输入层神经元数，a，b和c为待定系数，N为样本数。根据大量实验发现，待定系数取a∈(0.7,1)，b∈(0,0.2)，c∈[2,3,4,5]时效果较好。

2.2.3 递阶遗传自适应算子设计

在递阶遗传过程中有三个遗传操作算子，分别为选择算子、交叉算子和变异算子。选择算子的作用是保存群体中的优良基因，提高遗传算法的全局收敛性。交叉和变异算子的作用是提高种群的多样性，降低“早熟”现象的发生。

(1) 选择算子设计。为获得合理的选择算子，本文引入基于切断的轮盘赌选择优化策略。首先用轮盘赌选择的方式单独选中某个最优个体，然后在选定个体中相应地减少该个体比例的大小，重复以上操作，直至产生所有所需个体。其具体步骤如下：

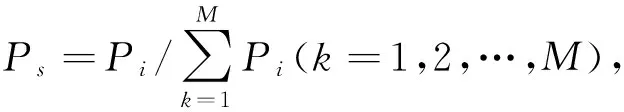
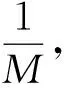
③若选出的个体数达到种群大小，则转(4)，否则转(1)；

④保存所有选出个体，结束。

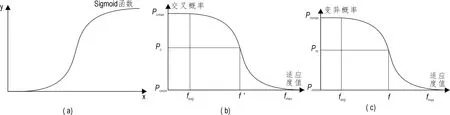
图3 Sigmoid函数及优化自适应交叉变异算子适应度曲线 Fig.3 The Sigmoid function, crossover and mutation operator adaptive fitness adjustment curve

(2) 交叉变异算子设计。Sigmoid函数是神经网络中常用的传递函数，其图形如图3中(a)所示，该函数的平稳和变化特征较为明显，在非线性行为间有较好的平衡趋势(Mennon et al.,1996)。基于这些特点，该函数能较好的解决传统交叉变异算子取固定值和线性变化值导致的遗传算法稳定性差及过“早熟”的问题(Siddique, 2014)。本文将Sigmoid函数引入到交叉变异算子的设计中，实现交叉变异算子的自适应非线性调整。式(3)、(4)分别为改进的自适应交叉和变异算子：

(3)

(4)

式中fmax和favg分别为种群的最大适应度和平均适应度，Pcmax和Pcmin分别为交叉概率取值的上、下限，f′为两个交叉个体中较大的适应度，f为所需变异个体的适应度，Pmmax和Pmmin分别为变异概率取值的上下限，A为系数。

如图3b,c分别为自适应交叉和变异算子适应度调整曲线，交叉和变异概率在favg处调整缓慢，有效提升适应度值接近平均适应度值的个体的交叉和变异概率。Sigmoid函数的引入改善了适应调整曲线中favg和fmax相差较大时趋于直线型的问题，保证了种群中较优个体的交叉和变异概率仍具有一定变化，避免了演化进程停滞不前。

2.3 AHGA-BPNN岩性识别流程

AHGA-BPNN岩性识别过程主要分为遗传迭代寻优和神经网络权阈值及网络结构赋值两大步骤。其算法流程如图4所示，主要步骤描述如下：

(1) 测井数据预处理，初始化自适应递阶遗传中的种群规模、最大迭代次数、染色体长度，以及神经网络中输入测井参数个数、输出岩性类别个数、隐藏层最大层数、隐藏层最大神经元个数和网络误差精度等待定值；

(2) 递阶遗传染色体编码；

(3) 自适应递阶遗传选择、交叉和变异算子操作，迭代寻优；

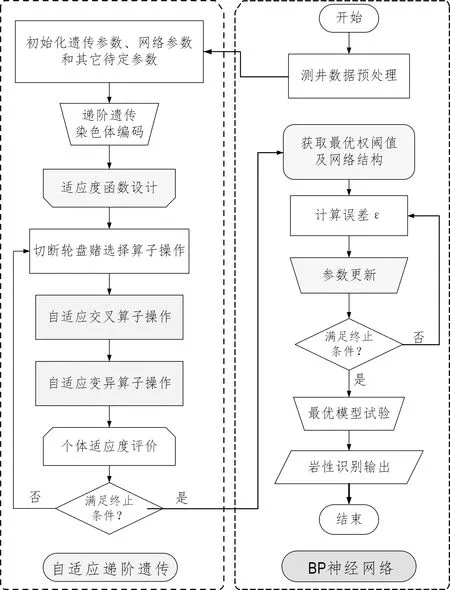
图4 自适应递阶遗传神经网络岩性识别模型Fig.4 Adaptive hierarchical genetic neural network mode of lithologic identification

(4) 适应度评价，获取最优个体；

(5) 最优个体染色体解码，为网络初始权阈值、网络结构和网络学习率赋值；

(6) 采用自适应递阶遗传优化后的神经网络对未知岩性部分的测井数据进行测试；

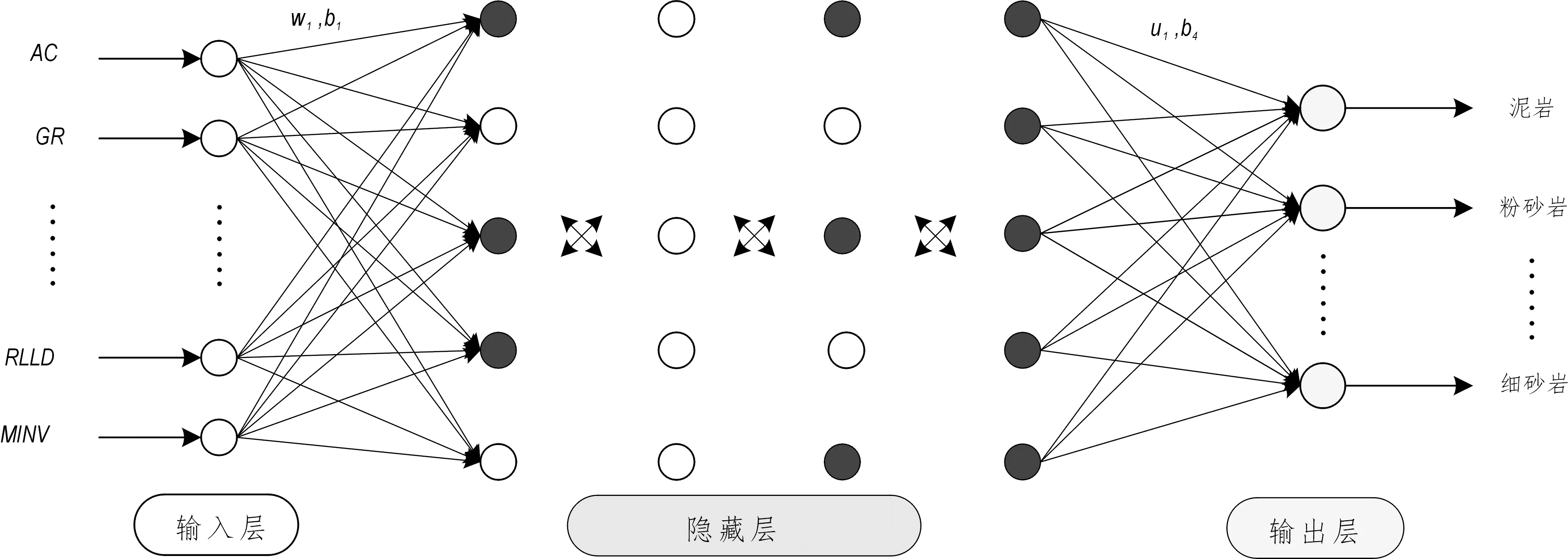
图5 实际测井资料下自适应递阶遗传BP神经网络示意Fig.5 Schematic diagram of hierarchical genetic Back-Propagation neural network for real well logging data

(7) 岩性识别结果输出。

3 应用实例

选取某研究区的实际测井资料验证本文提出的自适应递阶遗传神经网络模型的适用性。该研究区主要有泥岩、粉砂岩、含钙粉砂岩和细砂岩四大类岩性，收集该区100个钻井样本，随机打乱取前80个数据作为训练样本，后20个作为测试样本，样本输入为声波时差(AC)、自然伽马(GR)、微电位(MNOR)、微电极幅度差(ΔR微)、深侧向电阻率(RLLD)和微梯度(MINV)共6条对岩性影响较大的测井曲线数据，四种岩性编码成二进制形式作为神经网络的输出。

3.1 数据预处理

由于仪器、人为操作等因素导致实际测井资料中含有误差，因此，需要对测井数据进行预处理。首先进行测井资料环境矫正和岩性资料深度归位，然后对不同量纲的测井曲线数据归一化。

(5)

式中，X和X′分别为归一化前、后的数据，Xmax和Xmin分别为对应曲线的最大和最小值。预处理后数据如表1所示。

3.2 参数初始化

设定初始最大隐层数h=10，每个隐层最大神经元数l=12，则控制基因串长度(CGsL)=h*l=120，采用二进制编码。网络输入层神经元数n=6，网络输出层神经元数m=4，则参数基因串长度(PGsL)=6*12+10*12+12*4+4=292，采用实数编码。适应度评价函数待定系数取a=0.95，b=0.05，c=3。自适应交叉变异算子系数取A=9:903438，自适应递阶遗传种群规模M=120，遗传进化最大迭代次数g=500，网络误差精度ε=0.001，神经网络最大迭代次数epochsmax=5000。

3.3 测试结果分析

为了验证本文提出的AHGA-BPNN岩性识别模型的有效性，将测井数据随机打乱三次，重复进行3次实验，分别对标准三层BP神经网络(BPNN)、标准遗传算法优化BP神经网络(GA-BPNN)和自适应递阶遗传优化BP神经网络(AHGA-BPNN)三种岩性识别模型的收敛迭代次数、训练耗时、输出误差和识别准确率进行对比分析。

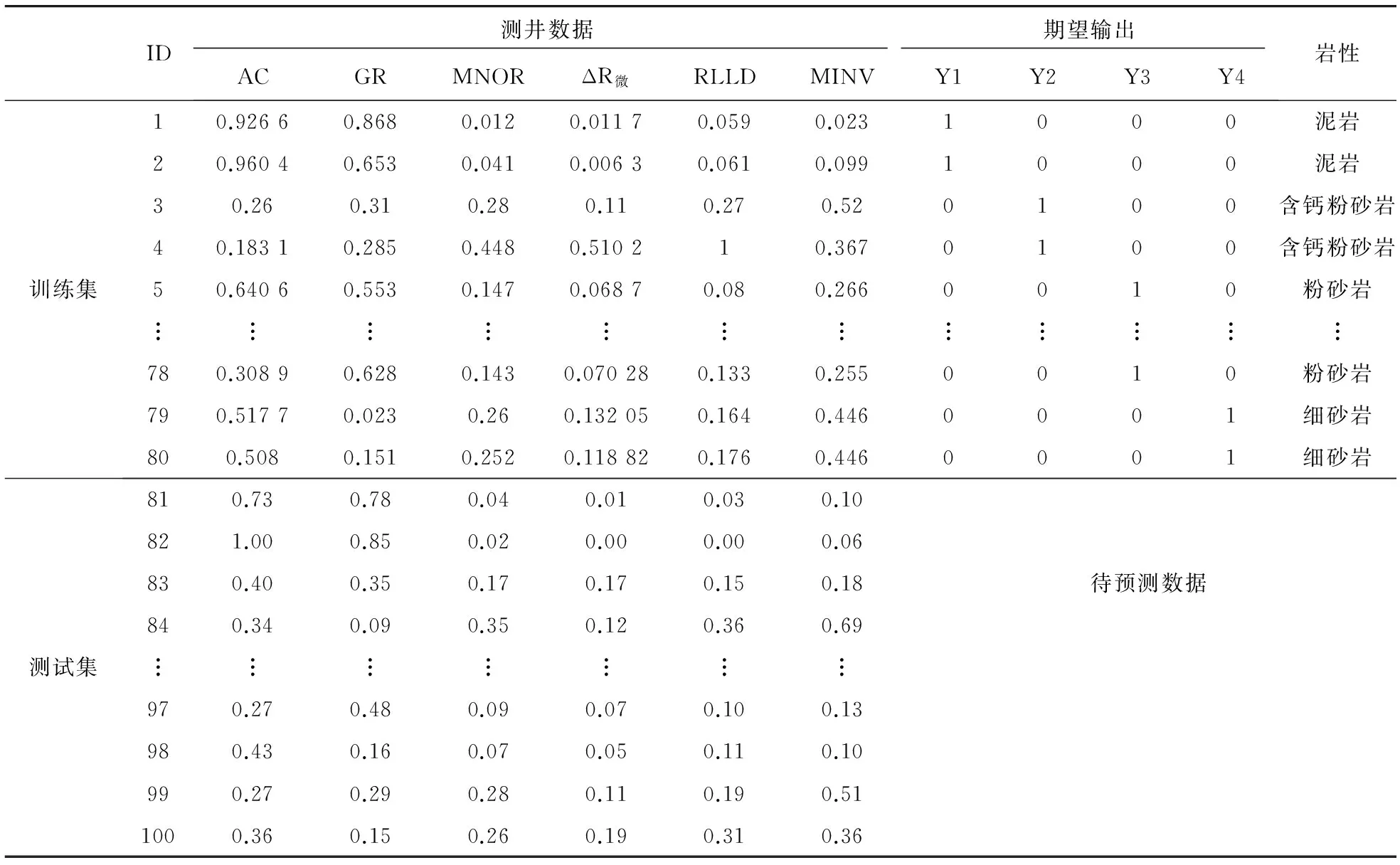
表1 训练集和测试集归一化处理后数据

三种岩性识别模型实验结果数据如表2所示，可知本文提出的AHGA-BPNN岩性识别模型的平均识别率达到95.67%，明显优于BPNN的65.67%和GA-BPNN的77.7%。

在迭代次数和训练耗时上，BPNN岩性识别模型三次实验平均迭代659次，平均耗时214 s；GA-BPNN岩性识别模型平均迭代221次，平均耗时104 s；AHGA-BPNN岩性识别模型平均迭代101次，平均耗时62 s。由实验结果可知，本文提出的AHGA-BPNN方法的收敛迭代次数、训练耗时和网络输出误差较BPNN模型均有较大缩减。

由图6可知，本文提出的AHGA-BPNN算法在实际岩性识别测试中所得结果与实际岩性情况完全相符，具有识别准确率高、收敛速度快和求解耗时短等特点，较其余两种方法的识别准确率有较大提高。

表2 三次实验结果对比

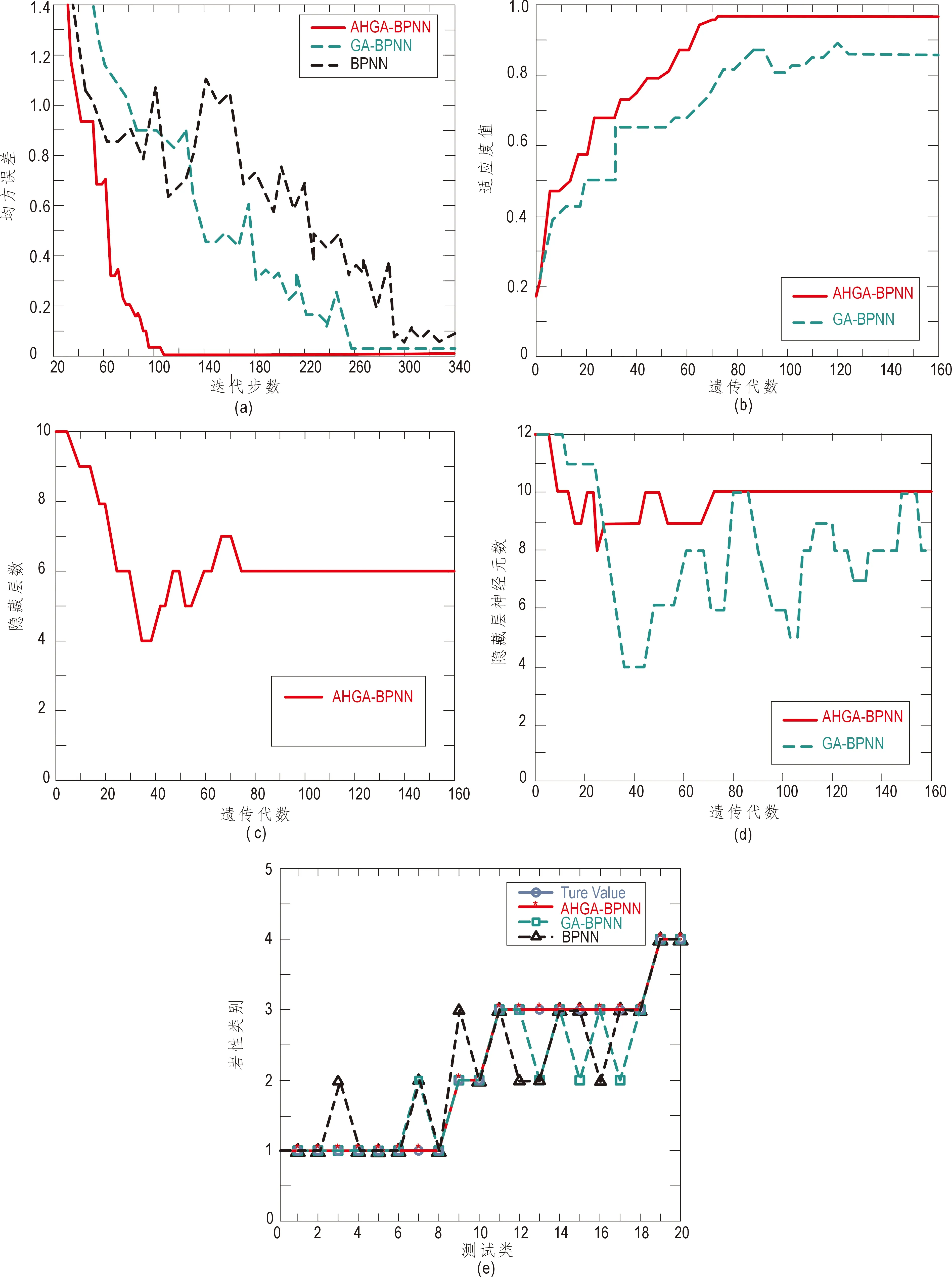
图6 实验结果Fig.6 The test resultsa.三种方法的均方误差变化曲线；b.AHGA-BPNN和GA-BPNN方法在遗传进化中适应度值变化曲线；c.AHGA-BPNN隐藏层数变化曲线；d.AHGA-BPNN和GA-BPNN隐藏层神经元个数变化曲线；e.第三次实验结果

4 结束语

本文提出的自适应递阶遗传神经网络实现神经网络传递参数和网络拓扑结构的同步优化，解决了传统BP神经网络收敛速度慢，网络结构参数选取困难等问题。自适应交叉变异算子依据适应度值和进化阶段进行自适应变化，有效提升种群多样性，使进化过程有效避免“早熟”现象的发生。将本文方法运用于实际测井岩性识别中，并与标准三层BP神经网络和标准遗传算法优化BP神经网络相比较，结果表明，本文提出的自适应递阶遗传神经网络岩性识别方法准确率高，训练速度快。总之，自适应递阶遗传神经网络岩性识别方法有效提升了储层岩性鉴别的精确性，为测井资料地质解释提供了一种新思路，在储层预测、油藏描述等领域有着重要的意义。

程国建，周冠武，王潇潇. 2007. 概率神经网络方法在岩性识别中的应用[J].微计算机信息, 23(6-1):288-289.

高美娟. 2005. 用于储层参数预测的神经网络模式识别方法研究[D].大庆：大庆石油学院:3-10.

王祝文，刘菁华，任莉. 2009. 基于K均值动态聚类分析的地球物理测井岩性分类方法[J].东华理工大学学报：自然科学版，32(2):152-156.

张治国. 2006. 人工神经网络及其在地学中的应用研究[D].长春：吉林大学:21-30.

Juprasert S, Jusbasche M, Sanyal S K. 1980. An Evaluation of A Rhyolite-ba S Alt-volcanic Ash Sequence From Well Logs[J]. Log Analyst, 12(1):10-20.

Ke J Y, Tang K S, Man K F, et al. 1998. Hierarchical genetic fuzzy controller for a solar power plant[C]//IEEE International Symposium on Industrial Electronics. Proceedings. ISIE. IEEE:584-588.

Mennon A, K Mehrotra, C K Mohan, et al.1996. Characterization of a class of sigmoid functions with applications to neural networks[J].Neural Networks,(9):819-835.

Simon O. Haykin. 2009. Neural Networks and Learning Machines, 3rd Edition[M].Prentice Hall PTR:25-30.

Sutton R S. 1986. Two problems with back-propagation and other steepest-descent learning procedures for networks[J]. Proc Cognitive Sci Soc, 12(6):48-56.

Whitley D. 1995. Genetic algorithms and neural networks[J]. Genetic algorithms in engineering and computer science, 3: 203 -216.