二阶复矩阵A，B酉等价的两个充要条件

岳 芹，赵建中

(1.皖西学院 金融与数学学院，安徽 六安 237012；2.皖西学院 经济与管理学院，安徽 六安 237012)

二阶复矩阵A，B酉等价的两个充要条件

岳 芹1，赵建中2

(1.皖西学院 金融与数学学院，安徽 六安 237012；2.皖西学院 经济与管理学院，安徽 六安 237012)

研究二阶复矩阵酉等价问题，得出了二阶复矩阵酉等价的两个充要条件。

酉等价；矩阵迹；矩阵谱；三角矩阵

酉空间是欧氏空间的推广[1]，酉空间中的每个酉变换对应着酉矩阵。酉变换在通信、雷达、声纳、地震学等领域有广泛的研究和应用[2](P88-91)。研究两个复矩阵能否酉等价有着重要意义，本文研究两个复矩阵酉等价的充要条件，先给出相关定义与记号。

1 定义与记号

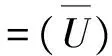
2 几个引理

引理1[5](P78-92)任何复矩阵A可相似于上三角矩阵，即存在酉矩阵U，使得U*AU为上三角矩阵。

引理2 若A，B为二阶复矩阵，则trA=trB，trA2=trB2与specA=specB等价。

证明 若specA=specB，记specA=specB={λ1，λ2} ，则

显然有trA=trB，trA2=trB2.

反之，若trA=trB，trA2=trB2,记A={λ1,λ2},B={μ1,μ2}，则

可解出，λ1=μ1，λ2=μ2或λ1=μ2，λ2=μ1因此 specA=specB.

引理3 若A，B为二阶复矩阵，则trA*A=trB*B，detA=detB与specA*A=specB*B等价。

证明同引理2。

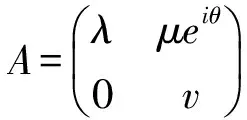
证明 显然当λ=v时后一情形变为前一情形. 在前一情形有

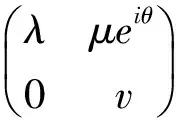
可知A和B也酉等价。若μ≠0,λ≠v，我们要求二阶酉方阵

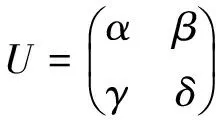
又

所以可取

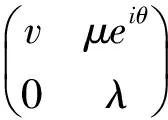
此即

(1)

(2)

(3)

于是由(2),(3)有

这证明了β及δ必须适合条件

所以可取β,δ适合

3 主要结果与证明

定理1 两个2×2复矩阵A，B称为酉等价的充要条件为

证明 若A和B酉等价，即B=U*AU. 已知U为酉方阵，所以UU*=U*U=I，于是B=U-1AU. 因此

trB=trU-1AU=trA

反之，若trA=trB，trA2=trB2，trA*A=trB*B. 我们知道任一复方阵可酉相似于上三角方阵，所以酉等价意义下我们无妨假设

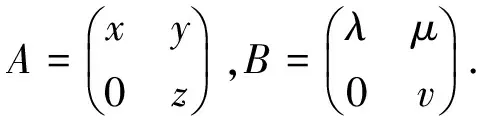
因此条件为

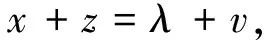
视λ,μ,v已知，来解出x,y,z如下：

由x+z=λ+v有x2+2xz+z2=λ2+2λv+v2，所以有xz=λv. 因此x,z为二次多项式

之根. 所以有两组解：

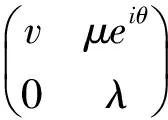
定理2 两个2×2复矩阵A，B为酉等价的充要条件为

specA=specB，specA*A=specB*B.

证明 若A,B为酉等价，由定理1证明过程知 trA=trB,trA*A=trB*BdetA=detB，再由引理2与引理3知 specA=specBspecA*A=specB*B.

反之，若specA=specB，specA*A=specB*B,则 显然有

由定理1知A，B为酉等价。

[1]Bermana, Plemmonsr J. Nonnegative Matrix in the Mathematics Science [D].New York: Academic Press, 1973.

[2]陈公宁.矩阵理论与应用[M].北京：科学出版社，2000.

[3]戴华.矩阵论[M].北京：科学出版社，2000.

[4]Chen G N. Note on Lower Bounds for the Rank of a Matrix [J].Linear Algebra Appl,1983(55): 125-132.

[5]李乔.矩阵论八讲[M].上海：上海科技出版社，1990.

Two Necessary and Sufficient Conditions for Unitary Equivalenceof the Second Order Complex Matrices

YUE Qin1, ZHAO Jianzhong2

(1.CollegeofFinanceandMathematics,WestAnhuiUniversity，Lu’an237012，China;2.CollegeofEconomicsandManagement,WestAnhuiUniversity，Lu’an237012，China)

Unitary equivalence problems of the second order complex matrices are studied, two necessary and sufficient conditions are obtained for unitary equivalence of the second order complex matrices.

unitary equivalence; matrix trace; matrix spectrum; triangular matrix

2017-03-12

2016年安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016240)。

岳芹(1978-)，女，安徽宿州人，硕士，副教授，研究方向：模糊数学、矩阵理论及应用。

O159

A

1009-9735(2017)02-0029-03