永磁同步电机匝间短路故障检测技术研究

陈慧丽,李 杰

(郑州科技学院,郑州450064)

0 引 言

随着新能源产业的发展,电动汽车(以下简称EV)系统得到了越来越多的研究,而EV的驱动装置广泛地使用了内置式永磁同步电机(以下简称IPMSM)[1-4]。但是由于IPMSM具有高电密运行的特点,其可靠性不是很理想,容易出现一些故障[5]。而EV的安全性要求越来越高,因此要求IPMSM更为可靠地运行。匝间短路故障(以下简称ISCF)是IPMSM的一种常见故障[6-7]。对于ISCF故障,为了提高电机运行可靠性,可采用故障检测技术,也是一种主动应对ISCF的方法[8]。通常,ISCF检测技术可分为在线检测方案和离线检测方案,通常前者得到了更多关注,因为其具有实时性。

目前现有的ISCF在线检测技术,多采用电气信号分析方法,少量的文献提出使用振动分析法[9-10]。在电气信号分析方案中,频域分析和时域分析都取得了不错的效果[11-12]。此外,各种新型的故障检测算法也不断提出,例如有限元分析法[13]、参数辨识法[14]和智能算法[15]等。但上述新型算法存在需要附加设备或计算量大等问题。对于用于EV的电机ISCF检测,存在一些特殊特点:首先,基于振动的方案受到EV工况的影响,故基于电气信号的方案具有优势;其次,考虑到系统成本和体积重量,不能使用多余额外地的设备。因此,迭代算法用于在线检测具有简单易行的特点,其可以集成到变频器控制器芯片中实现[16]。受限于变频器控制器芯片的处理速度,通常迭代算法需要简化,同时可以配合使用离线检测方法进行。文献[17]设计了一种感应电机驱动的EV系统离线ISCF检测方案,以保证EV安全运行。然而,对于EV高速循环工况,该方案的效果欠佳,仍需要设计对应的在线检测方案。

本文基于上述文献研究,提出了一种新型的EV用IPMSM的ISCF检测技术。新型ISCF检测技术集成了在线检测和离线检测两种方案,保留了两者的优点,最大限度地优化检测性能。其中在线检测采用了反电动势特征辨识简化迭代算法,即利用了二阶扩张状态观测器(以下简称ESO)简化了迭代过程。而离线检测采用了高频电压注入放大故障特征的方法大大调高了检测精度。此外,整个检测算法可以嵌入到变频器的控制器中,无需额外的附加硬件。最后,通过若干试验验证了新技术的有效性。

1 IPMSM ISCF系统

图1为IPMSM ISCF系统的结构框图。在线检测在电机运行时实施,而离线检测在电机停止期实施,但两者的信号采集是公共的。图2为新欧洲行驶循环[18](以下简称NEDC)图谱。在EV低速行驶循环工况,即0～800 s时间段,采用离线检测方案的效果优于在线检测方案;而在EV高速行驶循环工况,即800 s以后时间段,采用在线检测方案的效果优于离线检测方案。因此,在整个EV行驶循环工况,可以综合在线检测和离线检测的优势,实现检测性能的提高。

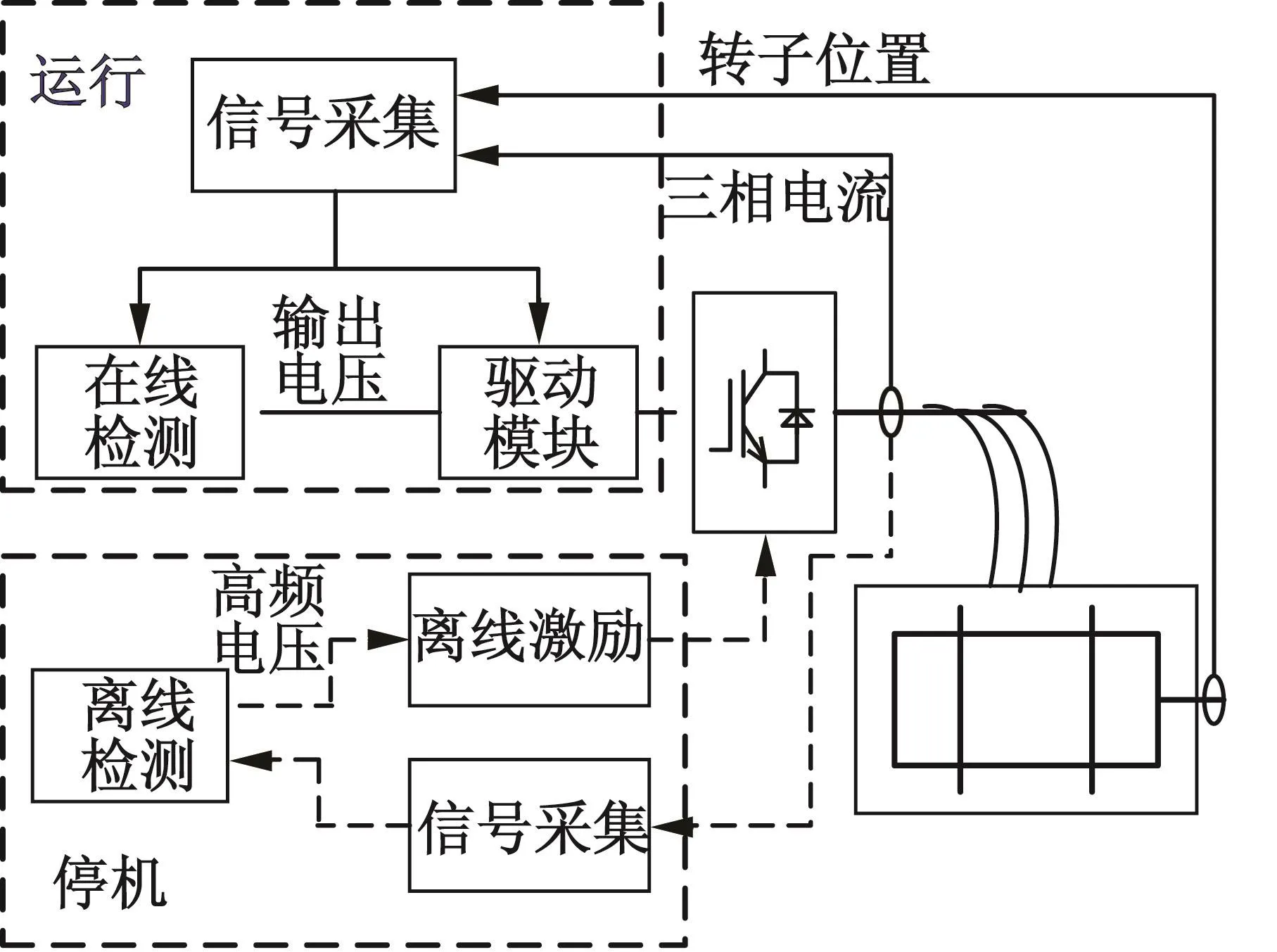
图1 IPMSM ISCF系统结构

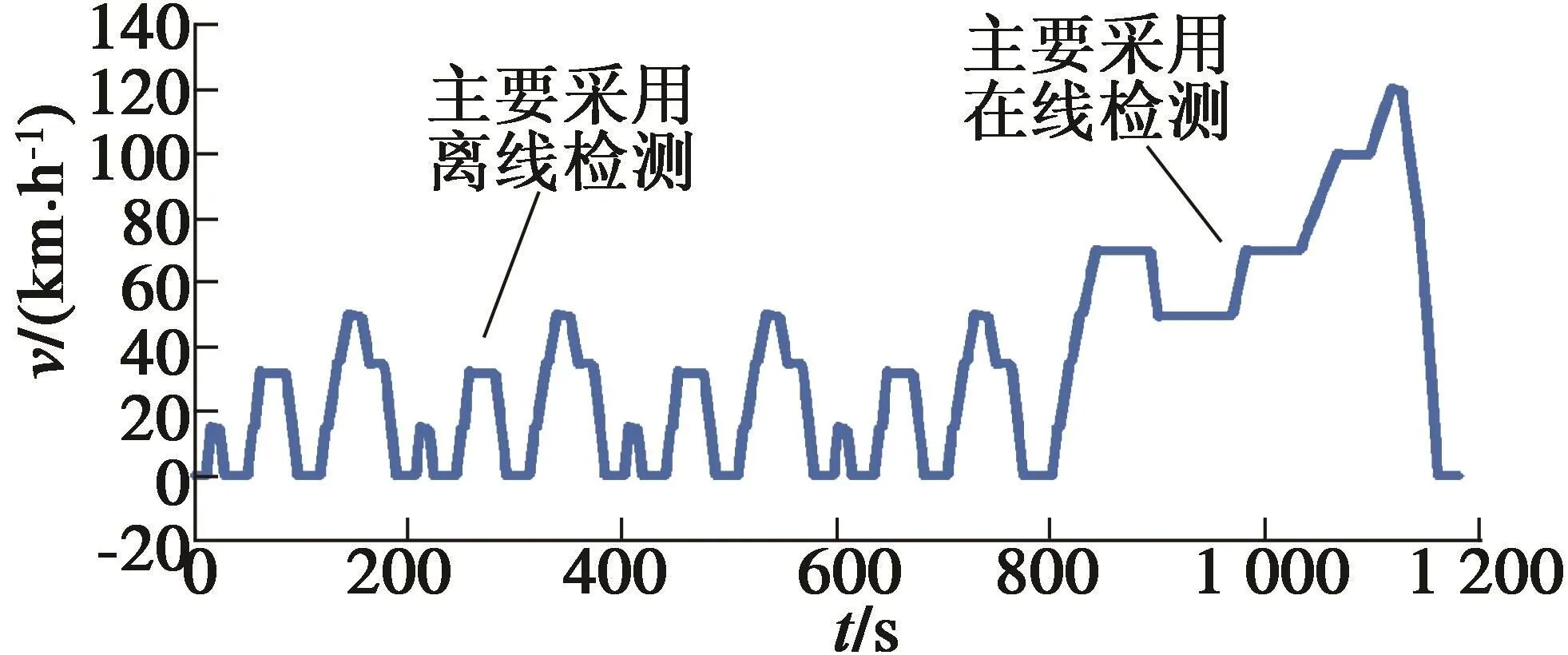
图2 典型车辆行驶循环

2 故障特征识别

图3为发生ISCF故障时的IPMSM绕组电路模型,不失一般性,设故障位于a相。故障绕组含有一个短路回路,短路电阻为Rf。进一步可将短路发生绕组分为两个电路部分,一是故障部分a1,而是正常部分a2。

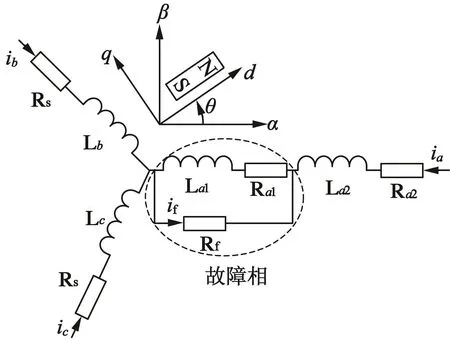
图3 ISCF故障时的IPMSM绕组电路模型

根据图3建立的IPMSM数学模型如下[19]:

式中:ua,ub,uc和un分别为电机三相定子电压和中性点电压;ia,ib,ic和if分别为电机三相定子电流和匝间短路故障电流;ψa,ψb,ψc和ψf分别为电机三相磁链和磁链基波分量幅值;Rs为定子每相电阻;LAA,LBB,LCC和MAA,MAC,LBC分别为电机三相自感和两相间互感;η为短路匝数与总匝数之比;ψ3h为磁链3次谐波分量幅值;θ为磁链矢量角。可以注意到,故障导致了中性点的平衡被打破,从而中性点电压un不为0。为了便于分析,修改旋转坐标变换矩阵:

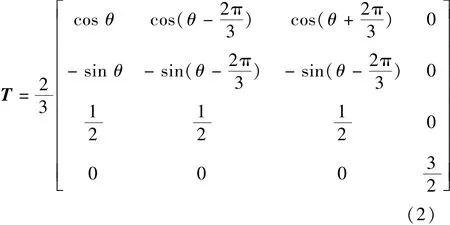
将式(2)运用到式(1)可得:

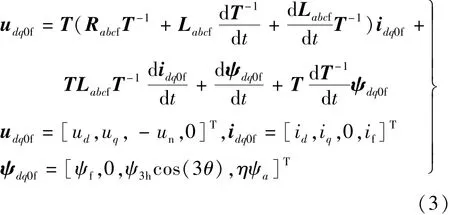
式中:id,iq和ud,uq分别为d,q轴电流和电压。

通过变换,电机的电压方程如下:

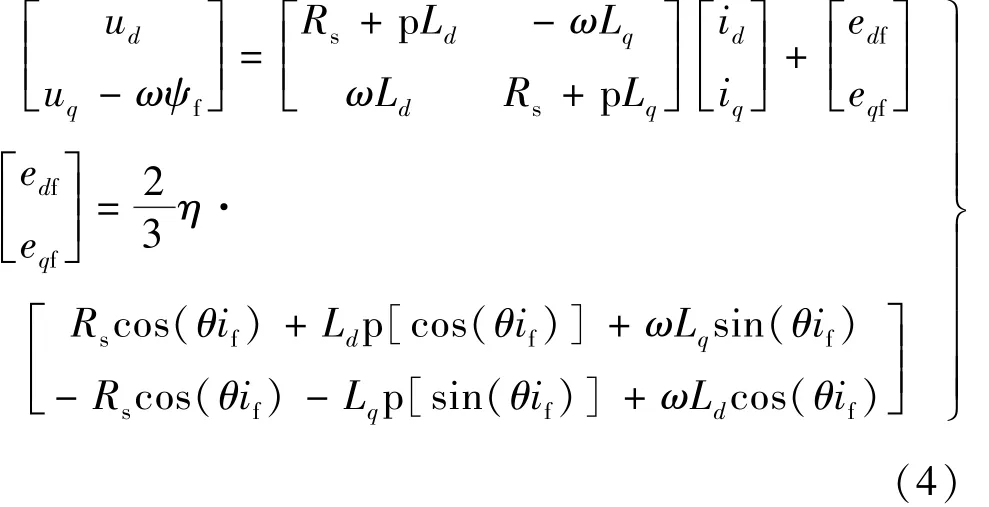
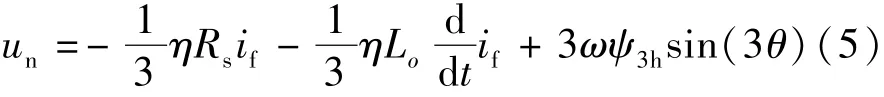
式中:p为微分算子;ω为基波角频率;edf和eqf为故障条件下电机反电动势的额外分量。

无故障时的IPMSM的电压方程:

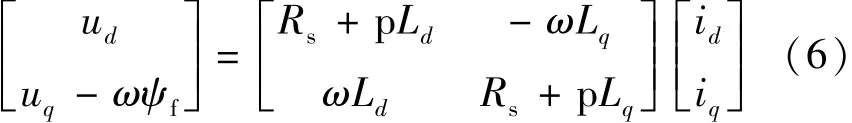
对比上式和故障时IPMSM的电压方程,可得知edf和eqf中包含了故障的相关信息。根据式(1),匝间短路电流if可简化:

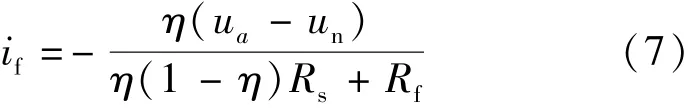
假设IPMSM工作在稳态,此时转速为常数,并且输入电压是对称的,即ud和uq,以及ω是常数,则a相电压可表示:

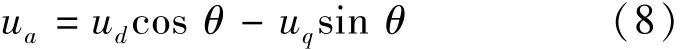
根据式(5)至式(8),if的稳态解:

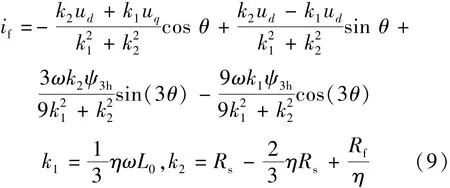
根据式(9)所得,可以求解故障条件下的电机反电动势的额外分量edf和eqf。已知这个额外分量分为直流分量和谐波分量,设edf和eqf的直流分量为Ed;E2hp和E2hn为2次谐波正序和负序分量;E4h为4次谐波分量。

由于E2hp反映了不对称程度,故将其作为ISCF检测的指标。而E2hp包含了两部分,一部分与基波分量相关,一部分与3次谐波相关。

对于E2hp来说通常基波分量占主导,因为其d轴电感Ld不等于 q轴电感 Lq,所以更适合用于IPMSM。

基于式(9)和前述分析,可以得到edf和eqf的解析表达式如下:

3 在线ISCF检测方案

在线ISCF检测方案需要考虑嵌入闭环控制系统,而闭环控制器中,谐波信息既存在于电机电压中,也存在于电机电流中。基于电流的传统分析法没有考虑电压中蕴含的信息,从而性能有所降低,故本文基于ESO和二阶广义积分(以下简称SOGI)设计了一种新型算法同时考虑了电压和电流中的谐波信息。

3.1 在线检测设计

引入的ESO是一种非线性观测器,通常用于估计系统扰动,但此处用于估计电机反电动势,具体如下:^

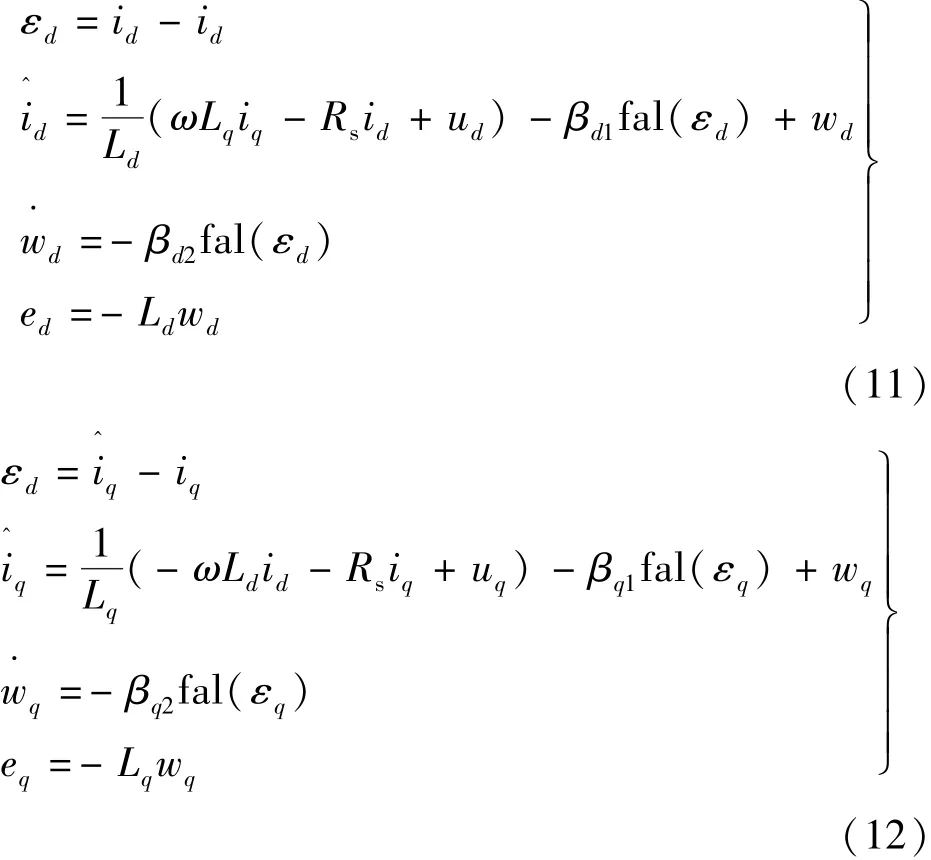
式中:ed和eq为ESO观测到的电机反电动势;εd和εq为d轴和q轴的ESO估计误差;wd和wq为d轴和 q轴的 ESO 估计扰动;βd1,βd2,βq1和 βq2为 ESO 的参数。而fal(·)为非线性函数,具体如下:

式中:sgn(·)为符号函数,α和 δ为 fal(·)的参数。当电机运行正常时,ed≈0和eq≈-ωψf;而当发生 ISCF 时,有 ed≈edf和 eq≈-ωψf-eqf。 先分析 ESO的稳定性。根据式(6)～式(11),ESO沿d轴的误差:

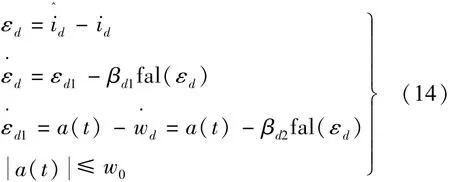
式中:a(t)为ESO沿d轴的有界外部扰动,不大于最大外部扰动w0;εd1为ESO沿d轴的总扰动。扰动通常是由参数和测量误差引起的,通常认为a(t)≈0。使用线性变换如下:

将式(15)代入式(14)得到:

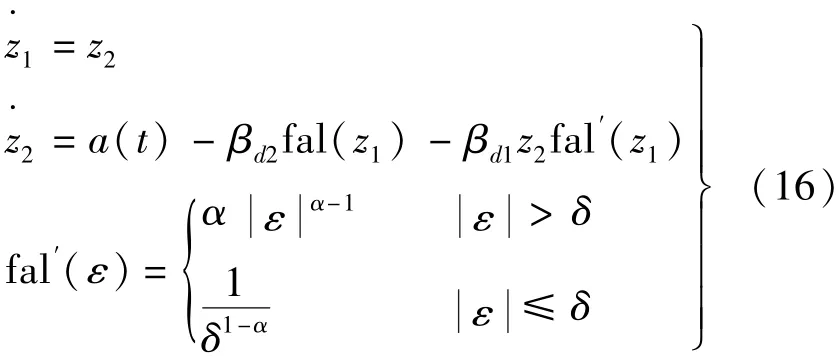
式(16)中可以看出,fal(ε)＞0,故设计 Lyapunov函数和对应导数如下:

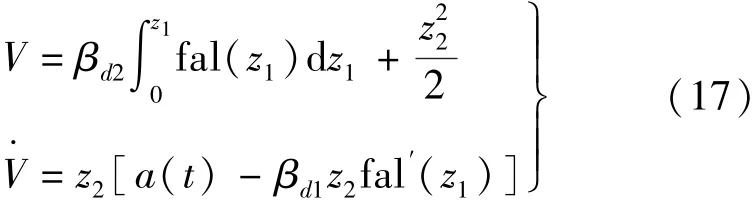
当a(t)=0时,Lyapunov函数的对应导数小于0,即系统是稳定的;若a(t)≠0,当满足以下条件时,系统依然保持稳定。

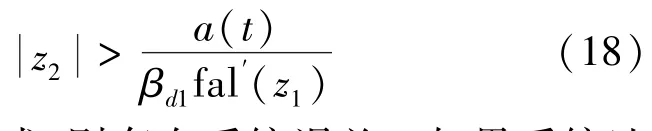
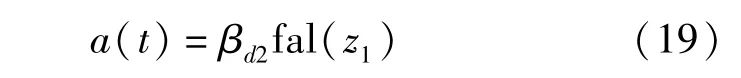
假设|a(t)|=w0,稳态误差范围:

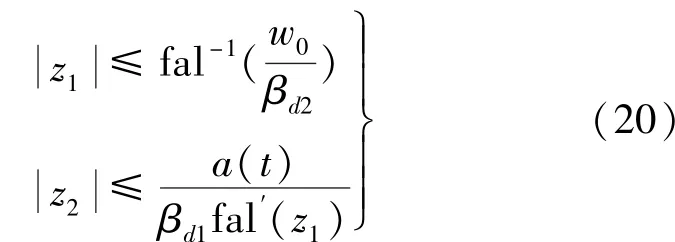
为了从估算的反电势中提取E2hp,应用逆旋转坐标变换可得到如下方程:

式中:eα和eβ为α-β坐标系下的估计故障电压分量;Eαβ3h为式(10)中 E2hn的 α-β 坐标系分量;Eαβn为式(10)中 E2hp的α-β坐标系分量。 然后对Eαβn实施SOGI算法,SOGI算法框图如图4所示。SOGI算法

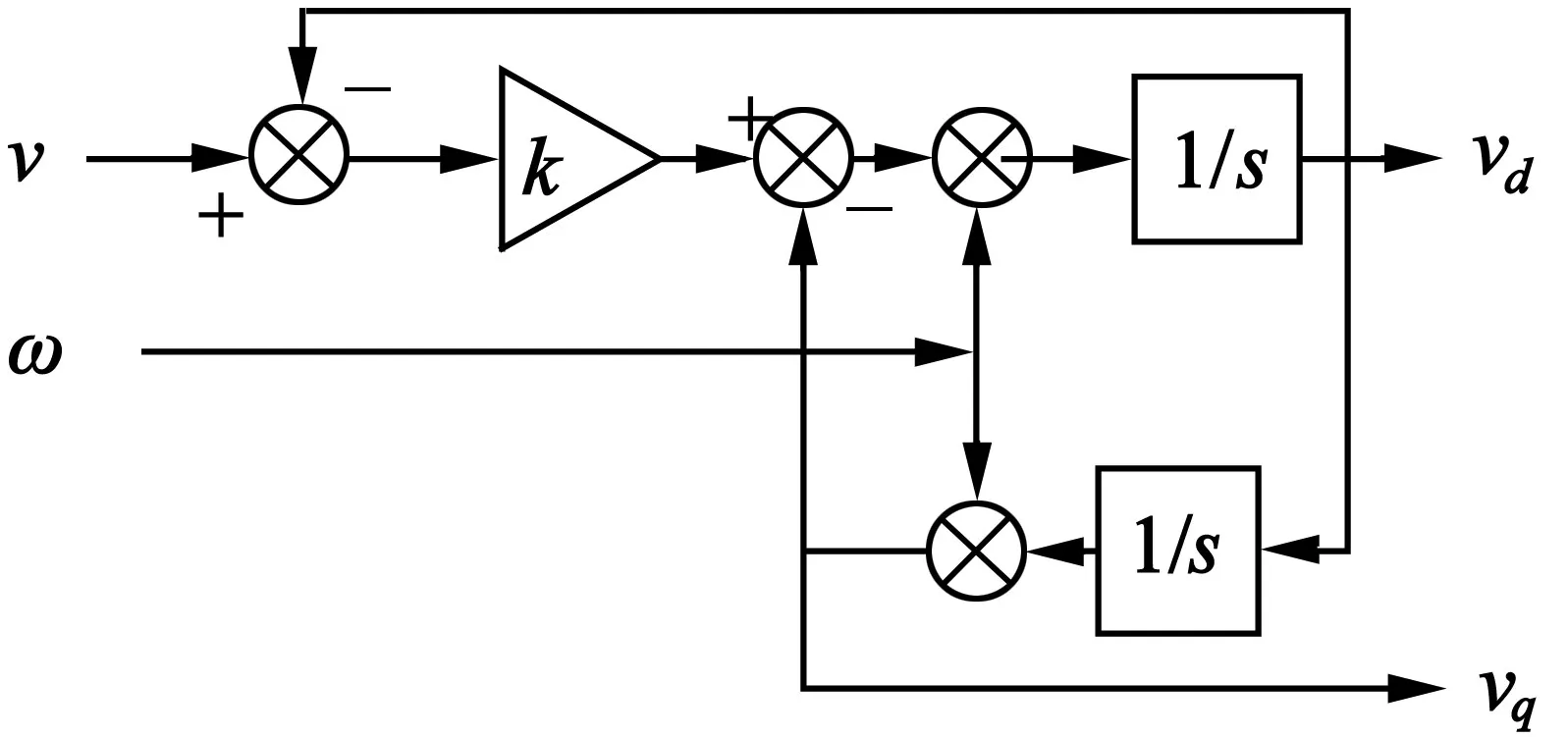
图4 SOGI算法控制框图

不仅能提取负序分量,还能滤除高频谐波。其传递函数如下:

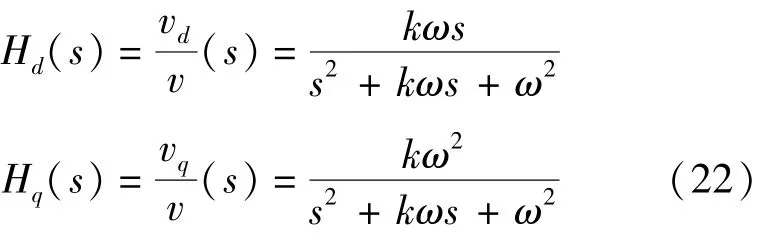
式中:k为阻尼系数,k增加将降低动态响应速度,但能提高滤波性能。图5为ω=100π rad/s,k=0.1时的波特图。具体负序分量传递函数Eαn(s)和Eβ(s):

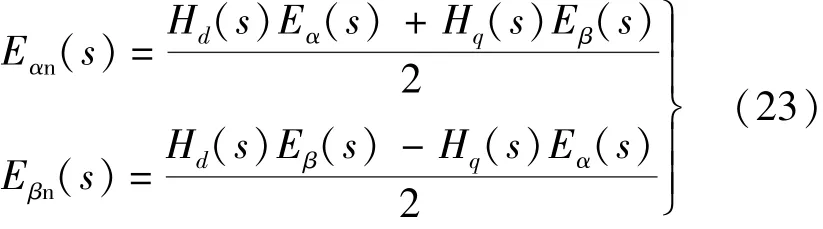
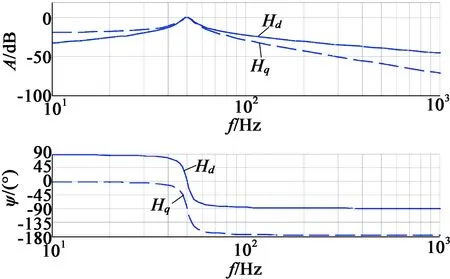
图5 SOGI算法波特图

3.2 故障判断与频率误差分析

通常,SOGI的输入频率和实际频率之间存在一个小误差Δω,这可能是因为采样引入的。假设SOGI的输入信号

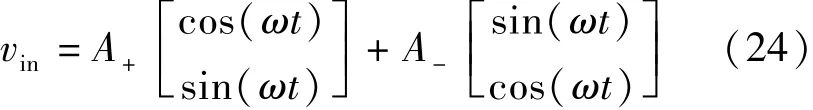
假设输入频率为则稳态输出vout:

从式(25)可以看出,Δω依然存在一个正序分量,故使用级联来解决这个问题,具体如图6所示,其中 eαn1和 eβn1是第一级计算后信号,eαn2和 eβn2是第二级计算后信号。最后,将负序分量幅值的平方作为故障指标,具体如下:

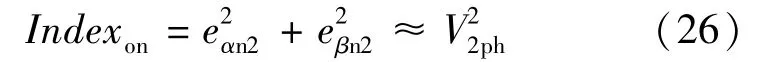
对于故障判断,设置了一个阈值用于消除干扰的影响。如果Indexon超过阈值,检测系统确定已发生故障。图6为在线检测的原理框图。

图6 在线检测原理框图

3.3 参数扰动分析

故障指标中近似可表示:

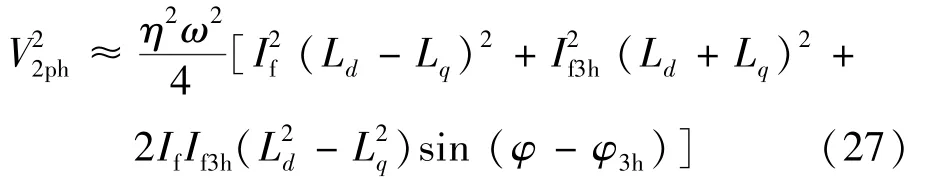
式(27)可以看出,正比于ω2,故检测灵敏度随ω降低而降低,同时ω降低还对应If和If3h较小,这导致低速时在线检测不灵敏。此外,当定子铁心饱和时Ld和Lq减小,这也不利于检测结果。因此,本文设置Ld和Lq为测量得到的常数,记为Ld,s和Lq,s。正常条件下,估计的电机反电动势如下:

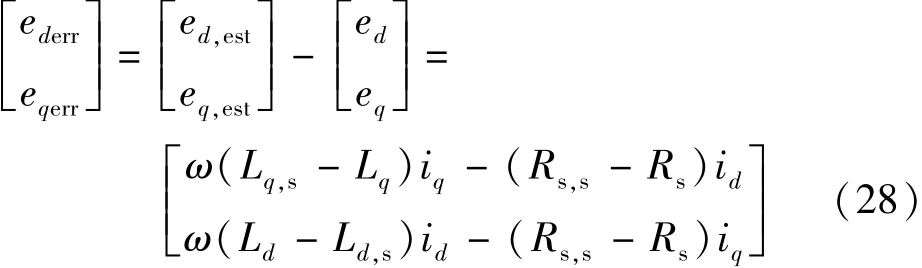
估计误差为一个直流分量,而式(23)所描述的二阶广义积分SOGI算法能够实现对直流分量的高阻,进而可以对其准确滤除。因此,参数扰动不能引起误检测。由于故障下很难获得估计误差的解析表达式,故为了简化问题,对开环系统进行分析,再将结论推广到闭环系统。在开环系统中,如果忽略Rs,估计的故障特征分量:

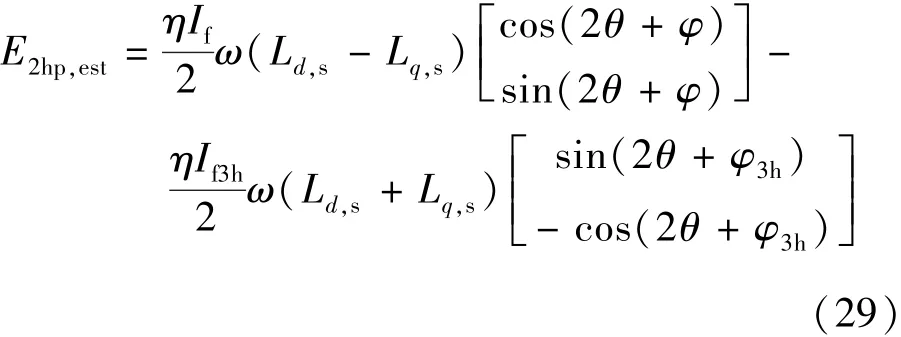
随着电流的增加,定子铁心趋于饱和,故有:

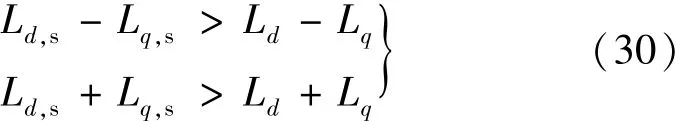
因此,可以得出结论如下:

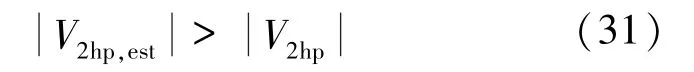
式(31)意味着估计误差可以放大故障特征,有利于检测更加准确。

4 离线ISCF检测设计

4.1 离线检测设计

离线检测的基本原理是利用高频电压注入放大绕组不平衡度,从而调高检测的精度,注入的高频电压 uαi和 uβi的表达式如下:

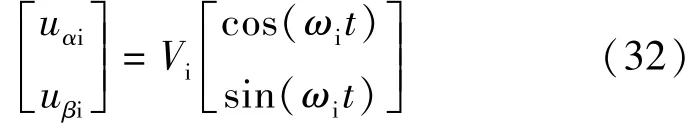
式中:Vi和ωi为注入高频电压的幅值和频率。如果电机状态正常,α-β坐标系下的IPMSM电压方程:

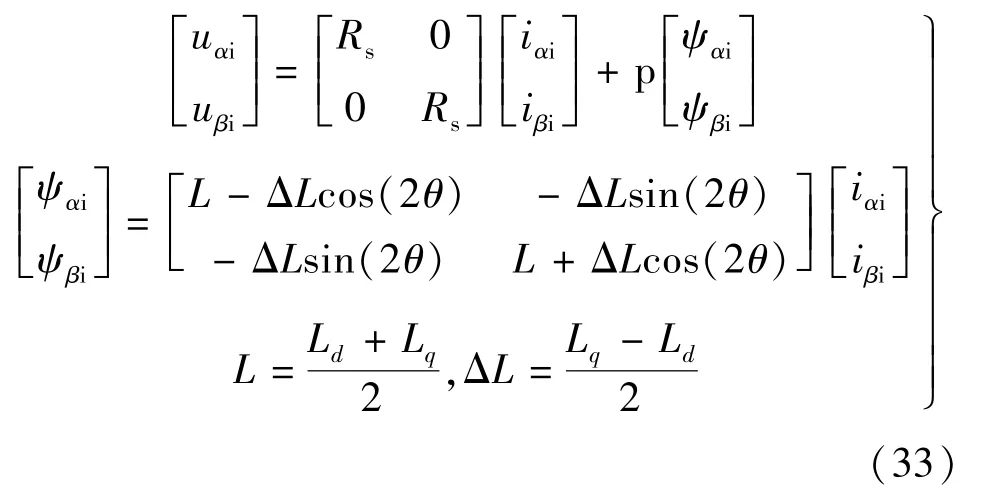
式中:ψαi和 ψβi为注入高频电压生成的磁链;iαi和 iβi为注入高频电压导致的高频电流。当电压频率足够高时,可忽略Rs的影响,故有:

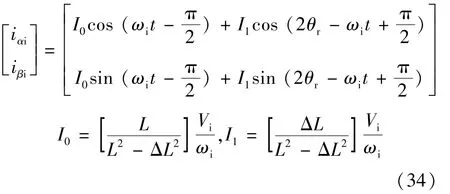
如果电机出现故障,则采用如下变换矩阵进行处理:

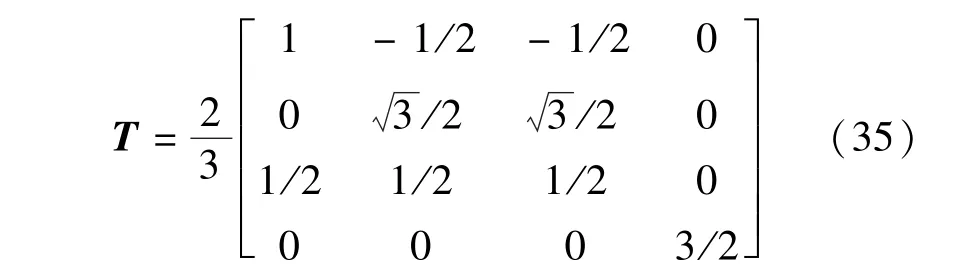
将上式运用到式(1),可得IPMSM在故障时的静态电压方程:

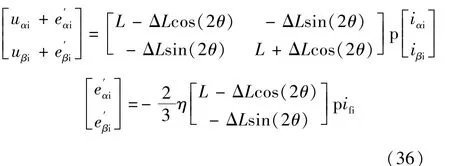
式中:eαi和 eβi为高频注入电压所致的扰动。 ua的表达式:

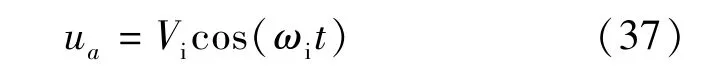
联立式(37)、式(5)和式(7),可以得高频注入下ISCF电流ifi如下:

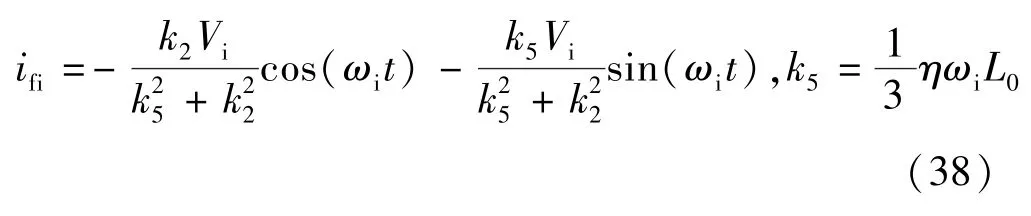
将式(38)代入式(36),可得故障条件下的电流响应

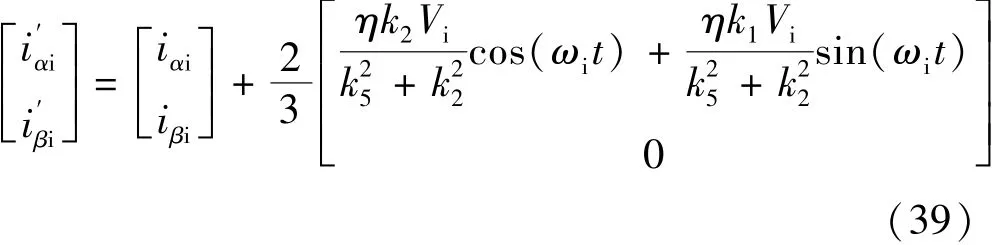
为了方便观测,引入了γ-δ旋转坐标系,其以角速度ωi旋转,具体如下:

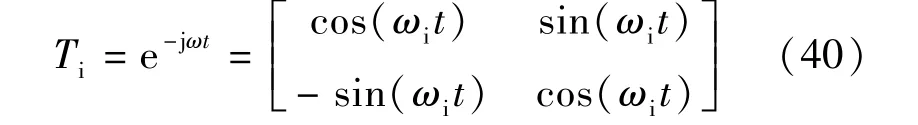
从而γ-δ旋转坐标系下电流iγ和iδ:

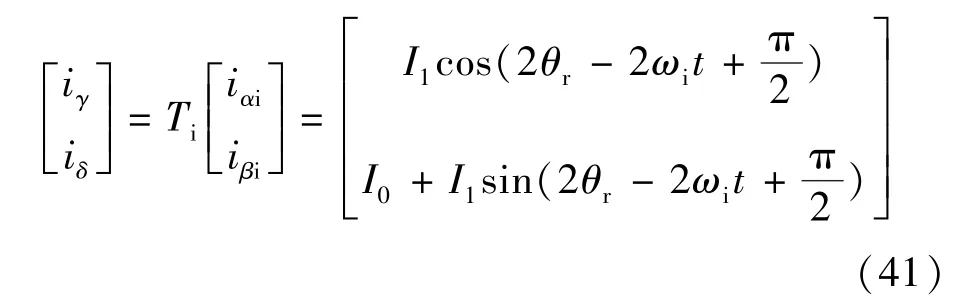
故障条件下的电流响应

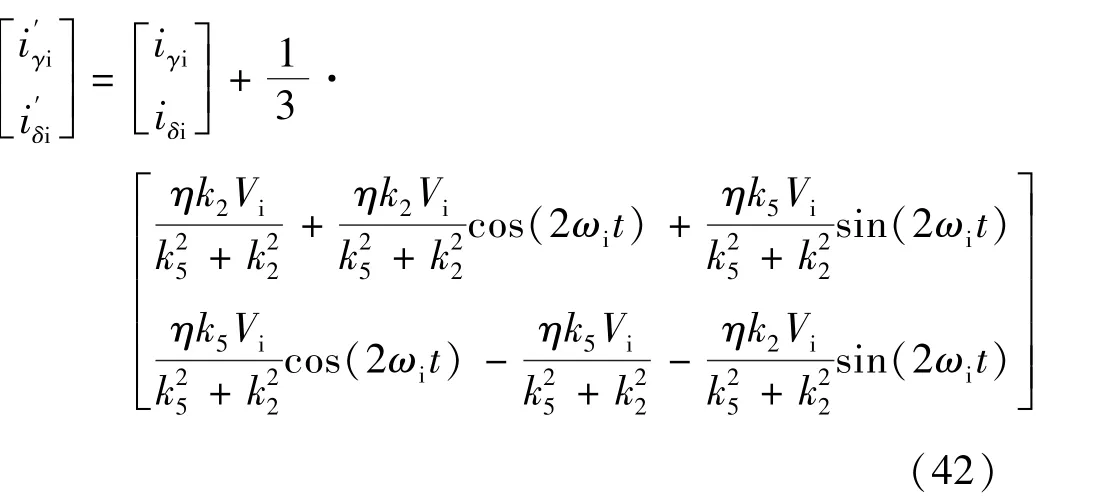
对比式(41)和式(42),可设计出离线检测的故障指标Indexoff如下:

式中:iγd为iγ的直流分量,通过低通滤波器可以得到,类似在线检测,使用了一个阈值来对抗扰动,具体的离线检测原理框图如图7所示。

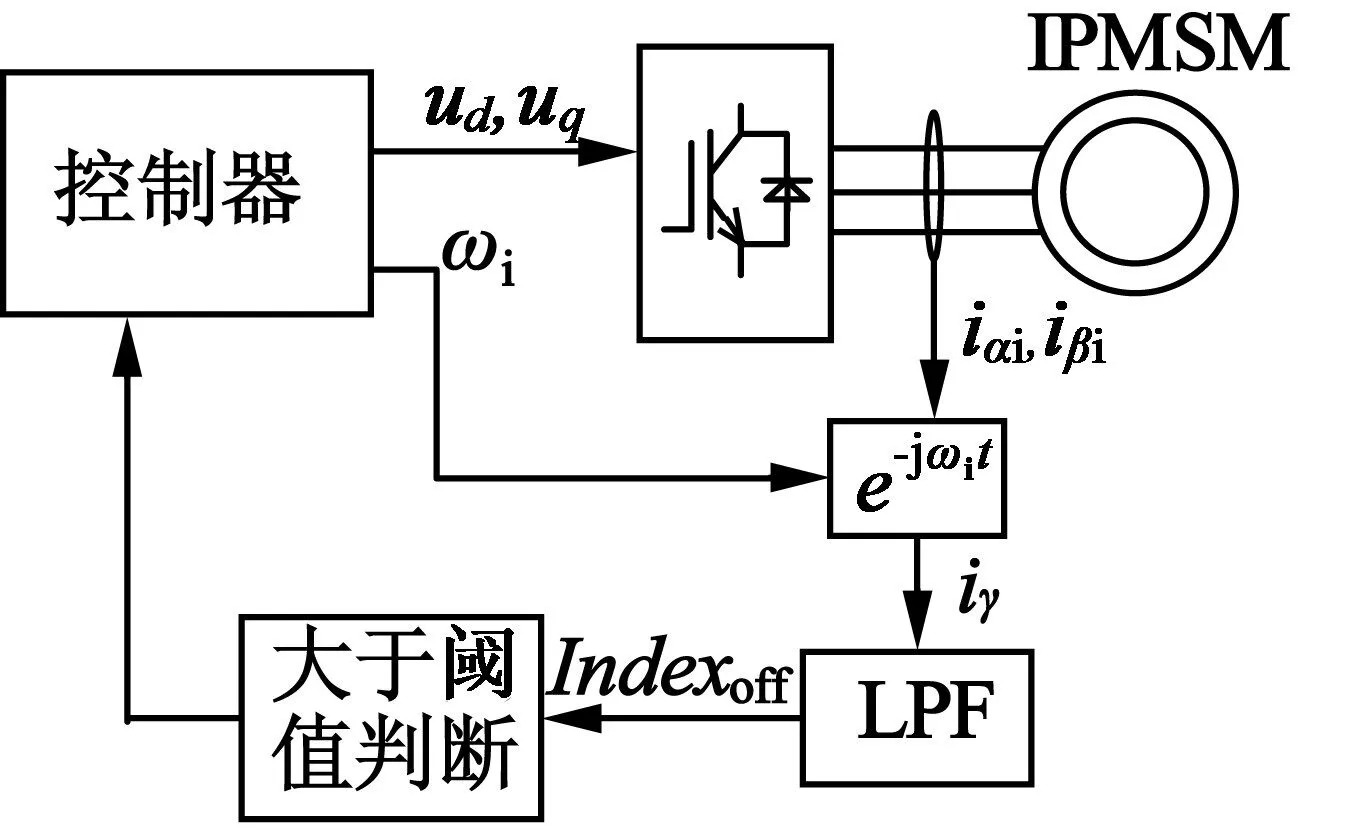
图7 离线检测原理框图

4.2 敏感度分析

如果ISCF故障轻微,则Rf较大或η较小,并有k2＞＞k5,Indexoff可近似为如下形式:

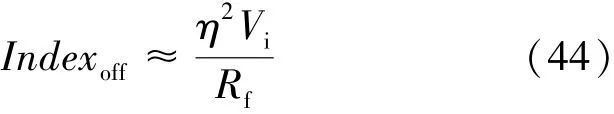
由上式可以看出,Indexoff不依赖于电机参数,而是由故障条件和Vi决定,而增大Vi可增加检测灵敏度,但增大Vi需要结合实际情况进行。此外,注入高频电压的频率也很关键,如果频率提高,Vi可以更大,但ωi受限于功率器件的开关频率,通常小于开关频率的十分之一。

5 试验验证

为了验证IPMSM故障检测算法的效果,开展了若干试验,试验平台构成如图8所示,电机参数如表1所示。

图8 试验平台

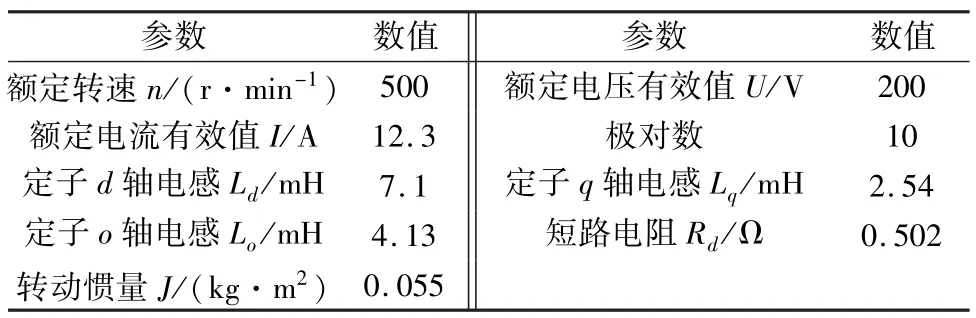
表1 IPMSM参数

故障检测算法的硬件载体为TI公司的DSP芯片TMS320F28335,而开关频率设为10 kHz。图9为IPMSM在额定转速下的空载反电动势波形和对应的频谱分析,其中基波幅值为147.1 V,三次谐波幅值为14.6 V。通过绕组引出触头可以设置不同的Rf值,非常轻微故障设置为20 Ω,轻微故障设置为10 Ω,一般故障设置为5 Ω,严重故障设置为2 Ω,而η固定为0.5。

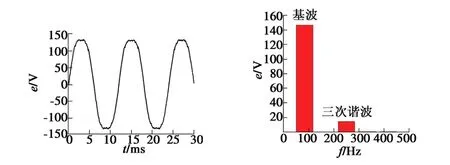
图9 IPMSM的空载反电动势波形及其频谱

在试验中,对于IPMSM的驱动控制,采用经典的磁场定向矢量控制,即设置d轴电流为0,而q轴电流设置为2 A,5 A和10 A代表轻载、半载和满载工况。ESO的参数为βd1=βq1=1 000,βd2=βq1=20 000,α=0.5和 δ=0.01,SOGI的参数 k=0.1,检测阀值设置为0.2。

(1)在线检测试验结果

图10为在电机正常和故障时满载工况下ESO的输出波形,图11为在电机正常和故障时eαn1,eβn1,eαn2,eβn2和 Indexon的波形。 从图中可以看出,在 SOGI第一级分离后,eαn1和 eβn1中仍然存在正序分量,但 SOGI第二级分离后,eαn2和 eβn2波形特征较好,能用于检测,从Indexon的波形来看,对于一般ISCF故障,算法具有较好检测效果。图12为不同负载工况下,以及不同Rf值下的检测结果。从图中可以看出,在不同工况下算法都具有较好的辨识度,但在低速下检测效果减弱,这验证了之前的分析,低速下需使用离线检测策略。图13为突发ISCF故障时在线检测的动态响应。从波形中可以看出,在250 ms内,算法能检出故障,具有较好的实时性。

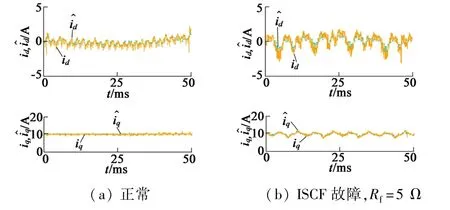
图10 在线检测中ESO的输出波形

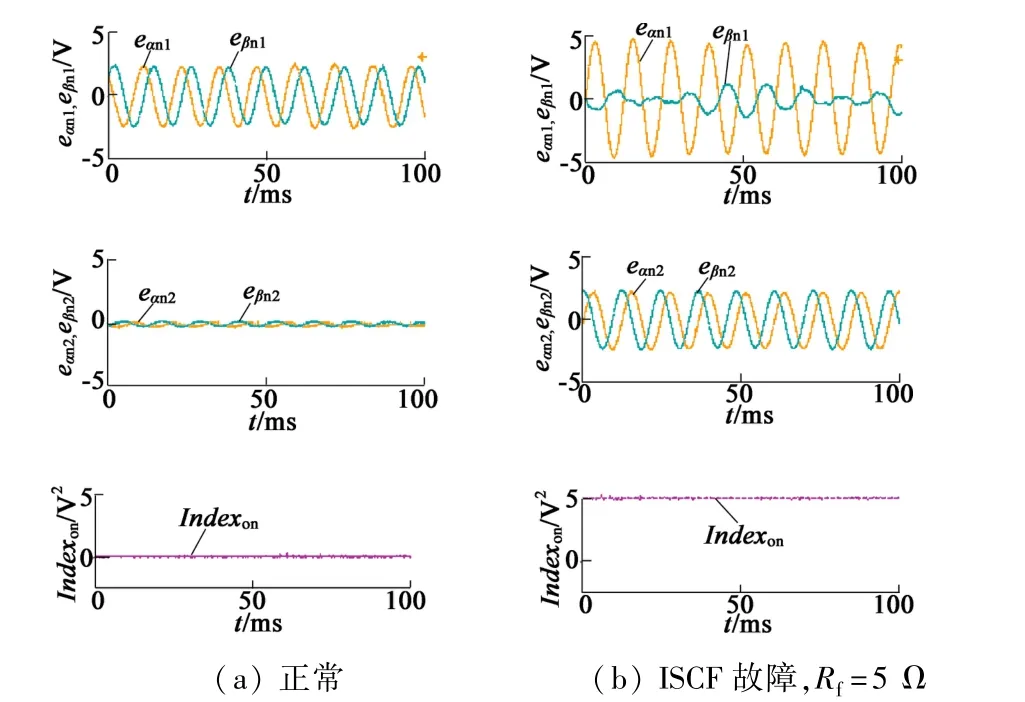
图 11 在线检测中 eαn1,eβn1,eαn2,eβn2和 Indexon的波形

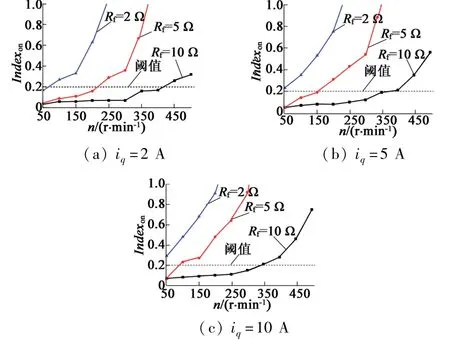
图12 不同工况下在线检测的结果

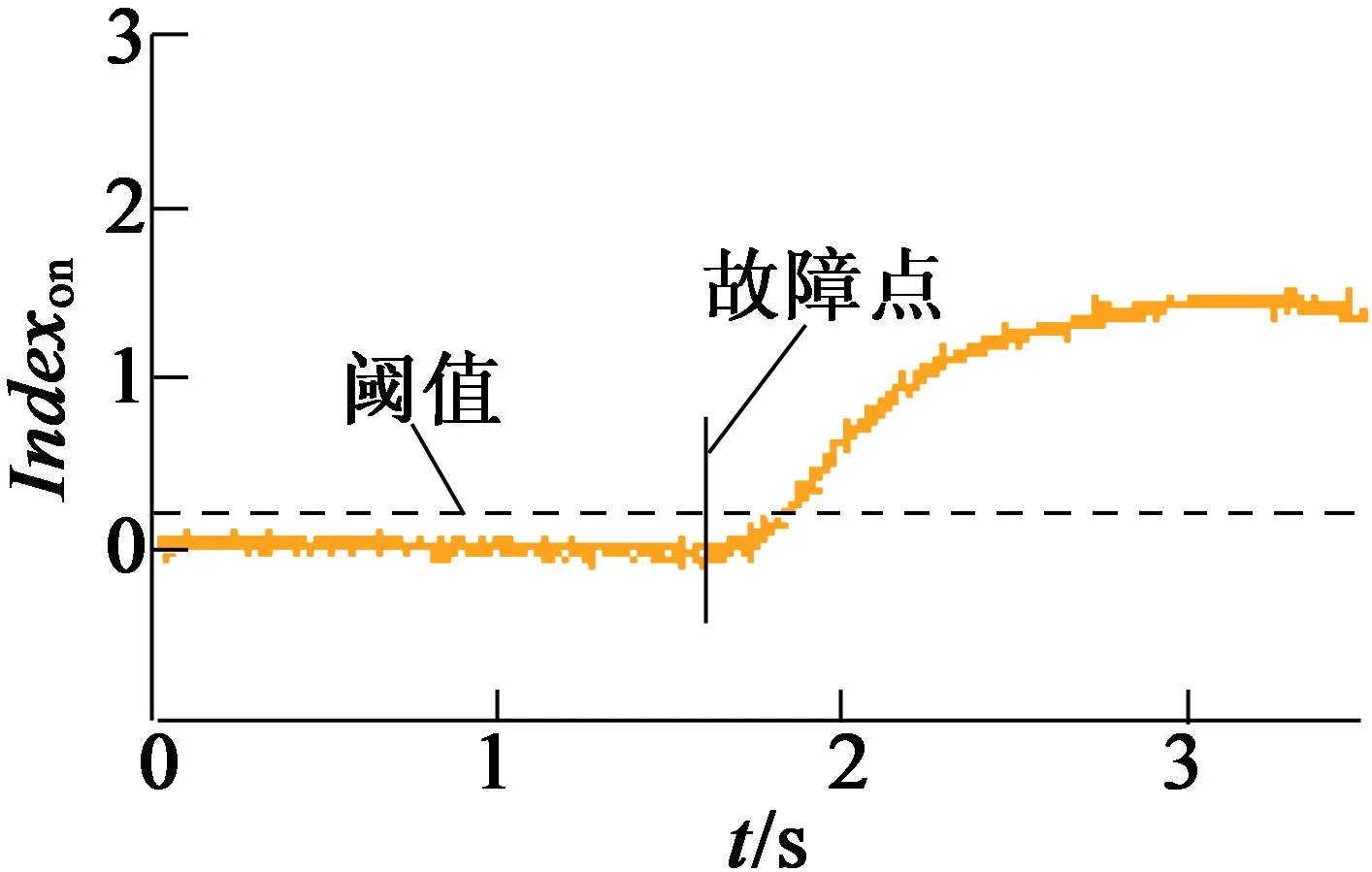
图13 在线检测的动态响应

(2)离线检测试验结果

进行离线检测试验时,注入高频电压的幅值Vi等于30 V,而频率可调,分别设置为200 Hz,300 Hz,400 Hz和500 Hz。图14为在不同频率和不同故障条件下的离线检测结果。从图中可以看出随着频率和短路电阻的减小,检测辨识度越高。这验证了前述分析。对比在线检测,离线检测的指标更好,即使在轻微故障条件下依然能准确地进行检测,而在线检测适合于一般故障和严重故障,从而离线检测是在线检测较好的补充。

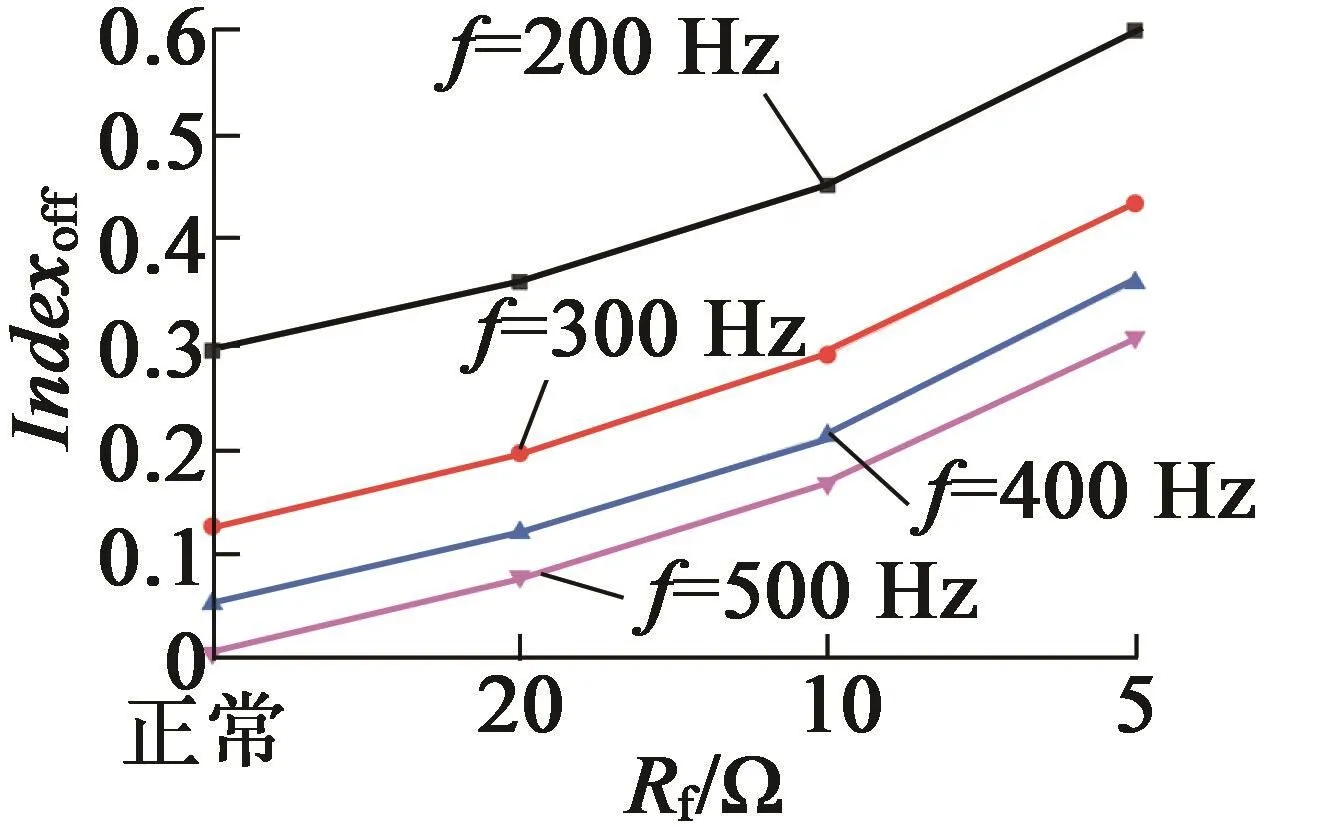
图14 离线检测的试验结果

6 结 语

本文围绕电动汽车用IPMSM的ISCF故障检测开展了研究,设计了一种结合在线检测和离线检测相结合的新型检测算法。通过理论推导和试验,可得到结论:1)新型检测算法综合了在线检测算法和离线检测算法的优点,在不同转速范围内就能获得较好的检测辨识度;2)试验结果验证了新型检测技术的效果,同时其无需额外的硬件配置,可嵌入到IPMSM驱动控制器中,降低了系统成本,提高了驱动系统可靠性。