永磁体削角削弱永磁同步电机齿槽转矩
2017-05-15杨晓冬白瑞林于圣龙
杨晓冬,白瑞林,于圣龙
(江南大学,无锡214122)
0 引 言
作为永磁电机固有的现象,永磁体磁场与齿槽相互作用,产生了齿槽转矩,进而产生振动和噪声,影响电机的控制。对于控制精度要求高的系统,比如高精度位置和自适应系统等,齿槽转矩是最需要考虑到问题之一[1]。
目前削弱齿槽转矩的方法有通过改变永磁体参数削弱齿槽转矩:极弧系数选择[2-3]、永磁体分段[4]、永磁体分块[5]、永磁体偏移[6]和改变永磁体形状[7-8]等;改变电枢参数削弱齿槽转矩:槽口偏移[9]、不等槽口宽度[10]和开辅助槽[11]等。文献[1]基于能量法和傅里叶变换,推导了开辅助齿情况下的齿槽转矩解析表达式,定量计算了辅助齿对齿槽转矩基波的影响,文献[5]采用叠加法分析了分块永磁体对表面式永磁电机齿槽转矩的影响,得到了永磁分块数、分块宽度以及分块间隔与总齿槽转矩的关系,文献[8]针对36槽的电机,提出了永磁体削角的概念,采用参数化扫描对比永磁体削角后和未削角时齿槽转矩的波形,指出可通过永磁体削角减小齿槽转矩。文献[12]针对无槽口的电机,推导永磁体削角后齿槽转矩的解析表达式,利用有限元分析了永磁体削角对气隙磁密和反电势谐波的影响。
文献[8]和文献[12]虽然都对永磁同步电机采用了永磁体削角削弱齿槽转矩,但文献[8]只针对一台电机做了参数化实验,未给出一般性的规律,文献[12]推导的削角后齿槽转矩的表达式没有考虑定子开槽对齿槽转矩的影响,所以本文进行以下工作:考虑定子开槽推导表贴式永磁同步电机在永磁体削角条件下的齿槽转矩表达式,提出采用永磁体削角削弱表贴式永磁同步电机齿槽转矩的永磁体削角长度比例系数确定方法,并利用ANSYS有限元分析平台在不同的电机上验证,证明所提出的方法是正确有效的。
1 齿槽转矩解析计算
在不通电的情况下,永磁电机永磁体磁场和齿槽相互作用产生的转矩为齿槽转矩,计算方法是电机磁场能量对定转子相对位置角的负导数[3],即:
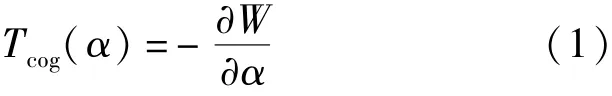
式中:W为气隙能量;α为定转子相对位置。
假设电枢铁心的磁导率为无穷大,磁场能量可近似为永磁体存储和气隙的磁场能量之和,因此W可以表达:

式中:μ0为真空磁导率。
气隙磁密沿电枢表面分布可表示:

式中:Br(θ),hm(θ),δ(θ,α)分别为永磁体剩磁,永磁体充磁方向长度和有效气隙长度。
将式(3)代入到式(2)得到:
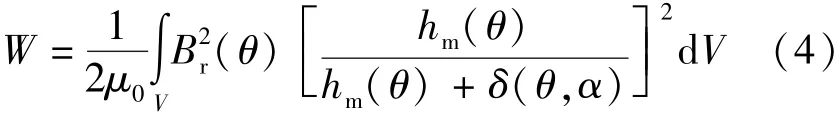
对B进行傅里叶展开,推导齿槽转矩的表达式,的 傅 里叶展开可以表示:
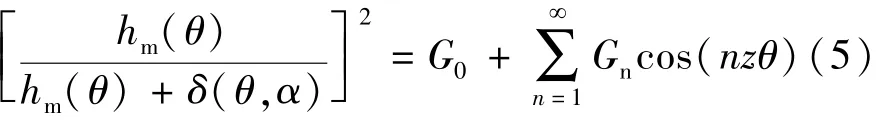
式中:z为槽数。Gn可以表示:

式中:b0为槽口宽度。
(θ)的傅里叶展开可以表示:

当m≠n时,三角函数在[0,2π]内的积分满足:将式(5)和式(6)代入到式(4),再代入到式
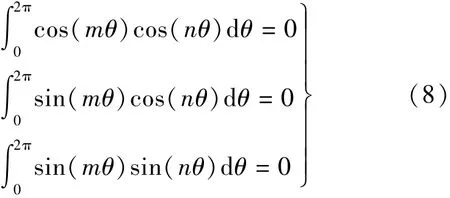
(1),结合式(7),得到齿槽转矩表达式:
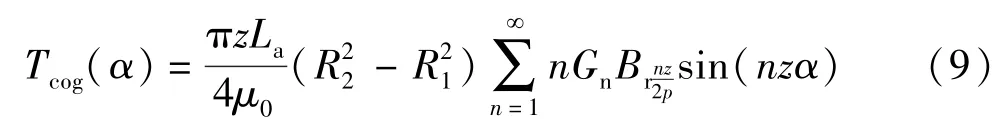
式中:z为定子槽数;La为电枢铁心长度;R2和R1为定子内半径和转子外半径;Gn为傅里叶分解系数;α为某一指定的齿的中心线和某一指定永磁磁极中心线的夹角;为傅里叶分解系数;n为使nz/(2p)为整数的整数。
由式(9)可以知道,通过改变磁极参数即改变对齿槽转矩起作用的的幅值,改变电枢参数,即Gn的大小以及电枢槽数和极数的合理配合这3种方法能削弱齿槽转矩。
2 基于磁极削角的齿槽转矩削弱方法
根据式(9)和文献[2]可知,当sin(nzα)为零时,理论上Tcog为零,所以将齿槽转矩削弱问题表示:

而n和Gn已知,所以推导永磁体削角后Brnz的
2p表达式。图1给出未削角和削角后永磁体的形状。图1(a)为等厚瓦片形永磁体,充磁方式为径向充磁;图1(b)为削角后的不等厚永磁体,充磁方式为径向充磁。对图1(a)的永磁体采用径向充磁时,因为充磁方向上长度一致,所以其表面的剩磁Br(θ)基本相等,可等效为矩形波。
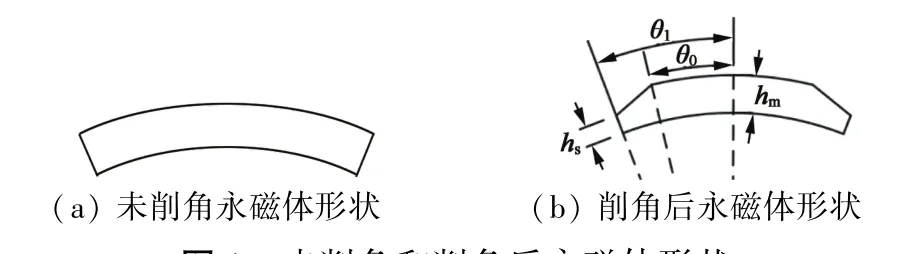
图1 未削角和削角后永磁体形状
对于图1(a)的永磁体,其削角方式如图1(b)所示,定义hs为削角的长度,削角的角度设为参数θ0。因此,气隙径向磁密分量可表示:
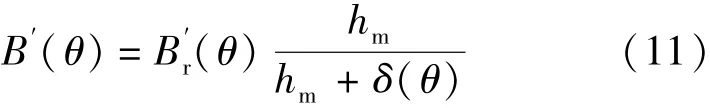
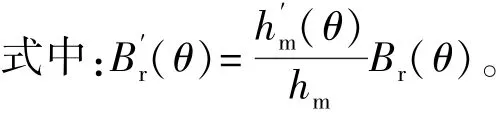
使用傅里叶变换推导得到的θ)各次傅里叶分解系数Brn表达式如下:

式中:h为削角长度hs与永磁体厚度hm的比值,定义为削角长度比例系数;θ1为永磁体的极弧系数对应的角度,即
因为n越大,Brn就越小[14],为了方便求解,只取Brn的前3次傅里叶分解系数,因此式(10)可化简:
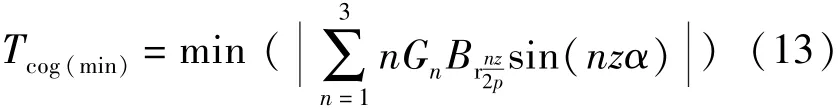
将式(6)和式(12)代入到式(13),而n和Gn确定,式(12)可以表示为关于h的二次函数,因此式(13)存在极小值,令式(13)为零,得到:

式中:

式中:n,p,θ1和θ0均为已知参数。
3 仿真验证
为验证永磁体削角方法的有效性,对4极18槽、4极24槽、4极30槽、8极9槽、8极12槽电机进行仿真实验,4极24槽电机参数如表1所示。
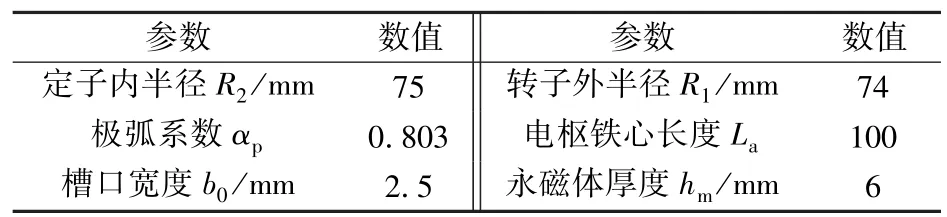
表1 4极24槽电机参数
θ0的取值分别为0.7,0.7,0.7,0.75,0.1时,经过计算得到h取值分别为:0.77,0.65,0.79,0.88和0.75。实验取一个齿槽转矩周期的数据,因为电机的槽数不一样,试验的仿真周期分别为10s,15s,6 s,5 s,15 s,电机转子的转速统一设置为1°/s,永磁体表面和定子内径的气隙网格剖分时应注意分层,且槽口的网格节点至少为4个,这样才能得到准确的齿槽转矩数据。利用以上数据,对4极18槽、4极24槽、4极30槽、8极9槽、8极12槽电机进行有限元空载仿真实验,最后得到的仿真结果如图2所示。
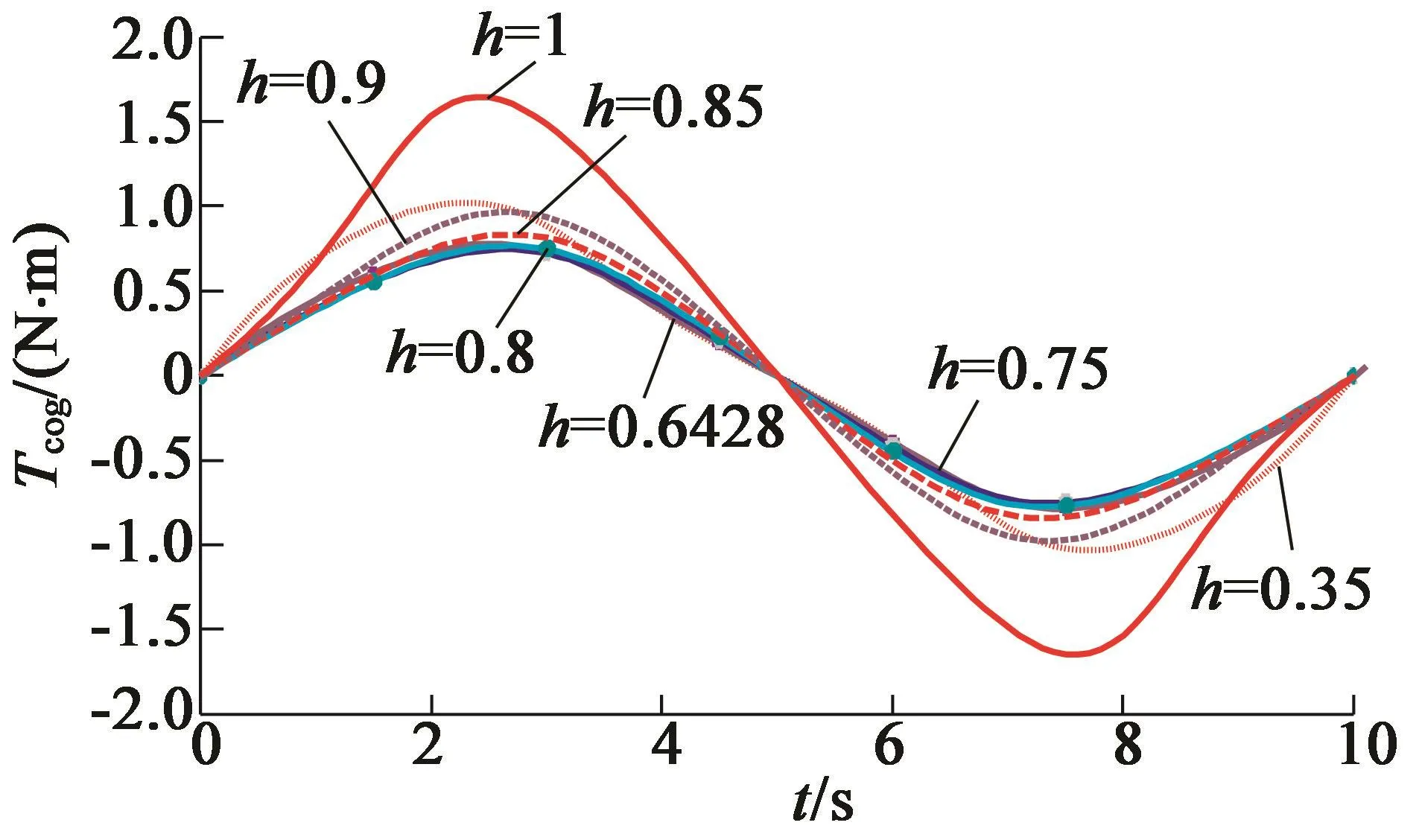

图2 不同槽数电机齿槽转矩
从图2可以看出,随着h的增加,齿槽转矩存在一个由大变小的过程,且取得最小齿槽转矩的h值与解析计算的结果存在差距,但差距较小。这是因为解析计算未考虑饱和漏磁的影响,同时也造成削角后齿槽转矩不为0。经过计算得到4极18槽、4极24槽、4极30槽、8极9槽、8极12槽电机的未削角和削角后的最小齿槽转矩数据如表2所示。
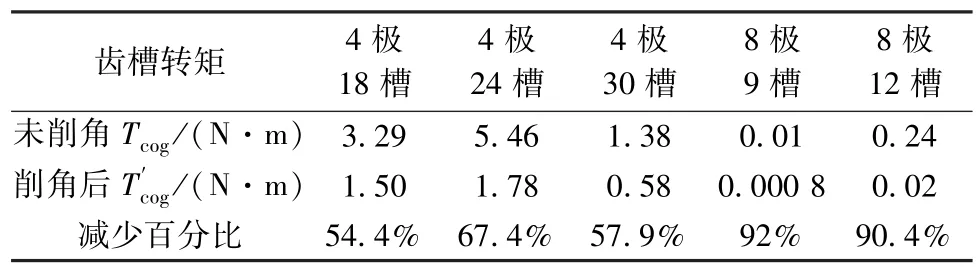
表2 齿槽转矩
同时,当h<0.6时,齿槽转矩是增大的,表明削角的长度不能小于0.6。此外,齿槽转矩取得极小值时,h取值是在0.6~0.95之间。从表3可以看出,永磁同步电机在其削角后,齿槽转矩最大下降了92%。
此外,永磁体削角可以改善反电势和气隙磁密波形,降低反电势和气隙谐波含量。利用ANSYS仿真得到4极18槽永磁体削角后气隙磁密波形,ANSYS实验结果如图3和图4所示,使用傅里叶变换得到表3和表4。

图3 4极18槽电机气隙磁密波形

图4 4极18槽电机反电势波形
图3 中h为1表示电机未削角,从表3可以看出,由于削角的影响,18槽电机气隙磁密的基波幅值都略有降低。式(16)为气隙磁密谐波含量计算公式,计算得到4极18槽电机气隙磁密谐波含量从未削角时的31.73%下降到h为0.75时的25.89%。

表3 4极18槽电机气隙磁密各次谐波幅值
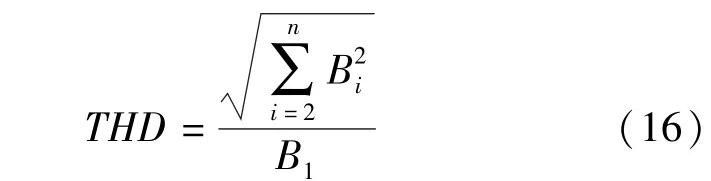
从图4可以看出,h为0.75时反电势波形顶部更平滑,计算得到4极18槽电机反电势谐波含量从未削角时的11.58%下降到h为0.75时的9.34%。从表4可以看出,虽然部分谐波次数对应的反电势幅值有所增加,但是由于3次谐波幅值下降,且3次谐波幅值所占的比重较大,所以不影响反电势谐波含量的变化。
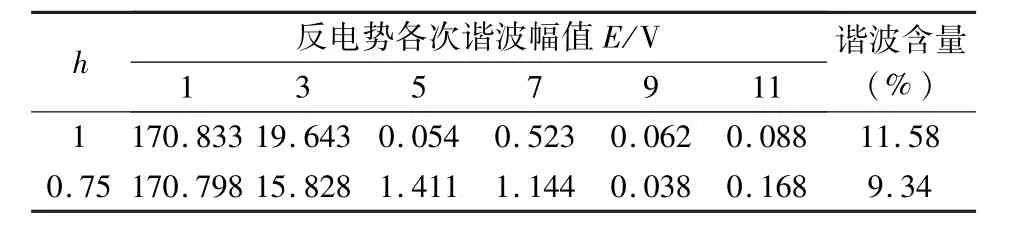
表4 4极18槽电机反电势各次谐波幅值
4 结 语
通过推导磁极削角条件下永磁体剩磁平方的傅里叶系数的表达式,用解析法计算了永磁体削角长度,比较了不同削角长度下齿槽转矩的幅值。由此得到以下的结论:
1)针对本文研究的4极18槽、4极24槽、4极30槽、8极9槽、8极12槽电机,永磁体削角可以减小电机的齿槽转矩。
2)齿槽转矩的幅值是随着削角长度的增加先减小后增大的。采用0.6~0.9永磁体厚度的削角长度时,齿槽转矩至少下降了54.4%。
3)永磁体削角改善了永磁同步电机的气隙磁密和反电势的波形,降低气隙磁密和反电势波形的谐波含量。
