一种减小开关磁阻电机振动的定子新结构
2017-05-15黄朝志陈海东刘细平杨国斌
黄朝志,陈海东,刘细平,杨国斌
(江西理工大学,赣州341000)
0 引 言
开关磁阻电机(以下简称SRM)是一种基于磁阻最小原理的定转子双凸极电机。转子采用硅钢片叠压形成,没有电枢绕组和永磁体,结构简单、抗冲击能力强。SRM由专用控制器驱动运行,具有效率高、调速范围宽、起动转矩大等优点,其应用已从电动车驱动,发展到家用电器、航空等各行业,有广泛的应用前景。然而,由于固有的双凸极结构和开关供电电源特性,SRM噪声和振动制约了其发展速度和应用领域[1-2]。
SRM的噪声和振动主要是由于定转子间脉动的径向和切向磁吸力引起。如何减小SRM的噪声,在控制方法上,文献[3]通过控制相电流的开通角与关断角,使径向力波的谐波分量不包含引起电磁共振的整数倍频率。Chi-Yao Wu等提出了两部换相法,将传统换相的电流关断过程分为两步进行,通过调整两次换相的时间间隔,消除定子的高、低频振动[4]。在电机结构方面,Kazuaki Nakata等提出了在转子齿中心开孔的方法,通过在转子齿中心开孔,改变磁力线的位置,降低定转子重叠部分的有效径向力,并证明了转子中心开孔降低径向力的效果主要取决于开孔宽度而非开孔厚度[5]。文献[6]将定子齿结构改为靴型以增加输出转矩并减小转矩脉动。张鑫等提出一种在转子齿两侧开槽的方法,通过开槽来改变转子顶部气隙磁密的方向,减小气隙径向磁密,抑制电机径向力波的同时增大切向磁密[7-8]。C.Picod等提出通过增加定子轭厚度来降低SRM定子的振动位移,从而降低振动[9]。
本文主要从电机本体结构方面研究SRM振动和抑制问题。首先分析SRM振动产生的原因,从麦克斯韦张量法和电磁能量守恒方程两方面推导径向力的影响因素,提出在定子齿顶部沿极弧方向开设矩形槽的方法,并从开槽宽度和深度上分析对减小径向力的影响;在圆形定子轭周边外接正8边形,增加定子振动固有频率,减小振动位移。
1 SRM振动分析
SRM运行时在定、转子磁极间存在磁场力。定、转子极上的磁场力可以分解为径向和切向两个分量。其中,切向分量是与电磁转矩相对应的作用力,而径向分量并不产生有效的转矩,所导致的定子形变是定子振动和噪声的主要来源。当径向力谐波与定子固有频率接近或达到一致时,将产生激烈的振动和噪声。因此,分析并减小径向力是控制定子振动的关键[10]。
在线性假设下,径向磁吸力可以表示:
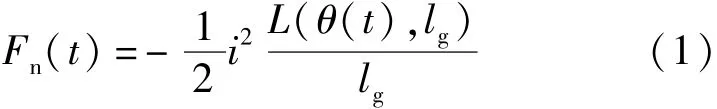
单相电磁转矩可表示:
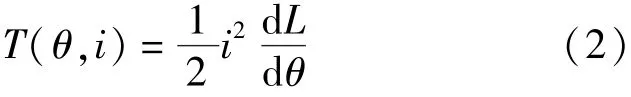
当SRM的单相绕组通电励磁时,定转子间产生径向磁吸力;在励磁电流被切断时,径向磁吸力减为零。随着SRM励磁绕组的连续换相,径向磁吸力重复地对定子轭作吸引和释放运动,这种运动激发共振频率,产生振动。脉动的切向力引起的转矩脉动也会产生振动和噪声。如果能有效地抑制径向力、降低转矩脉动,就能达到减小SRM的振动和噪声目的。
2 径向力和切向力分析
2.1 麦克斯韦应力法
麦克斯韦张量法是用等效的磁张力来代替体积力,从而可以有效地计算交界面上的磁场力。如图1所示,SRM转子同时受到径向和切向上的磁场力[11]。
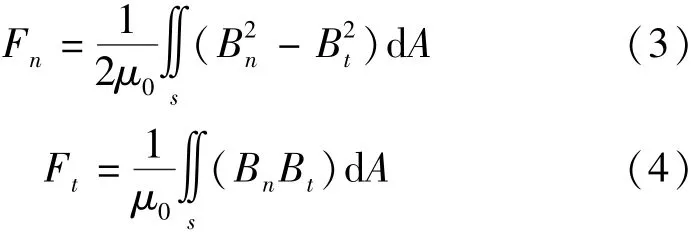
式中:μ0为真空磁导率;Bn为径向上的磁密;Bt为切向上的磁密。
可以看出,SRM的径向力分量和切向力分量主要由径向磁密和切向磁密决定。又SRM的气隙切向磁密远小于气隙径向磁密,电机受到的径向力也是远大于切向力,因此,在降低径向磁密的同时增大切向磁密,才能在降低径向力的同时减小对转矩的影响。
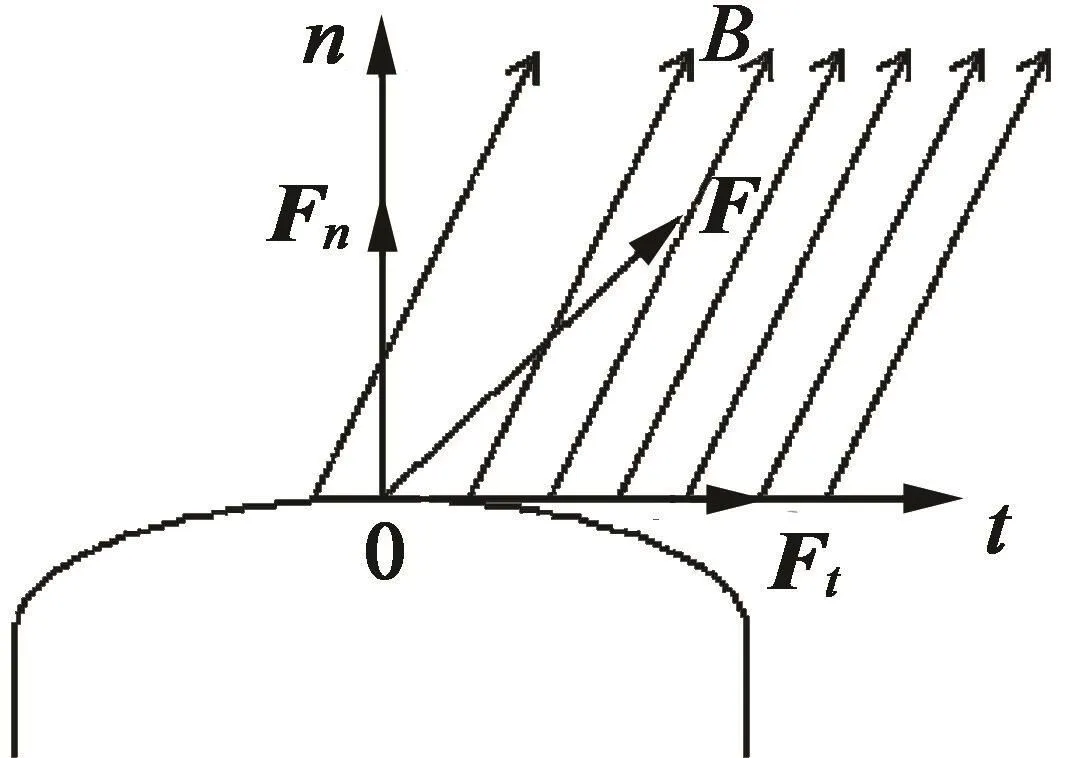
图1 应力示意图
2.2 能量分析
从能量的角度对SRM径向切向力的分析[13],电场的输入增量:
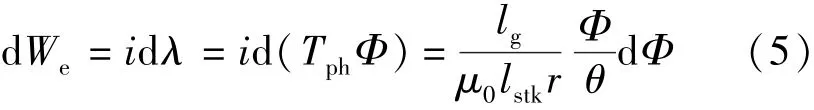
式中:Tph为一相的线圈匝数;θ为定子转子的重叠角度;lstk为电机轴向长度;r为转子外径;lg为气隙长度。则磁场中的储存能量:
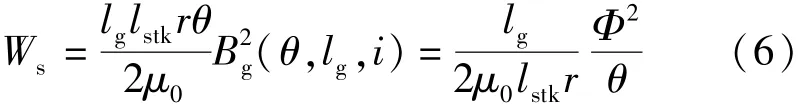
忽略铁损和涡流损耗等,能量平衡方程:
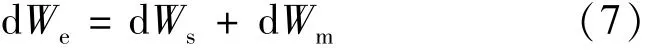
切向力所产生的转矩:
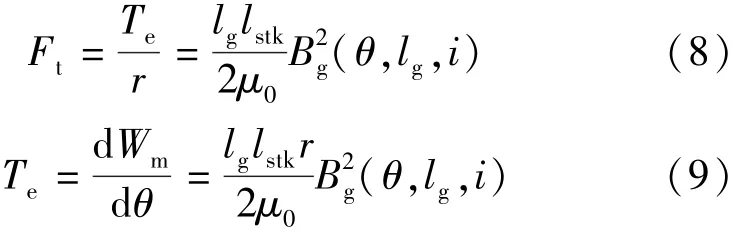
径向上产生机械能:
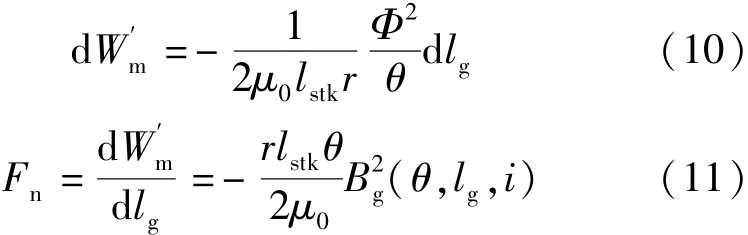
在定子与转子完全重合部分,电感最大,径向力最大。径向力产生在定子齿与转子齿的重叠部分,切向力产生在两个重叠面积的边缘。定转子重叠部分所产生的径向力为有效径向力,该径向力是造成SRM振动的主要因素。
为此,本文提出一种定子开槽新结构,在定子齿顶沿定子极弧开矩形槽。将定子齿与转子齿重叠区域的磁力线朝着非重叠区域挤压,从而改变定转子间径向力的作用位置,较大幅度地降低有效径向磁吸力。
3 Ansoft仿真分析
3.1 磁路分析
本文以三相8/6极,额定功率1 kW,额定转速1 500 r/min的SRM为例,进行了结构优化。样机的主要参数如表1所示。
由于SRM轴向长度远大于气隙,定子上有集中绕组且端部较短,定转子铁心采用叠片结构,端部效应小,求解区域存在电流源。综合以上特点,对SRM的有限元分析常采用矢量磁位,并进行如下假设:
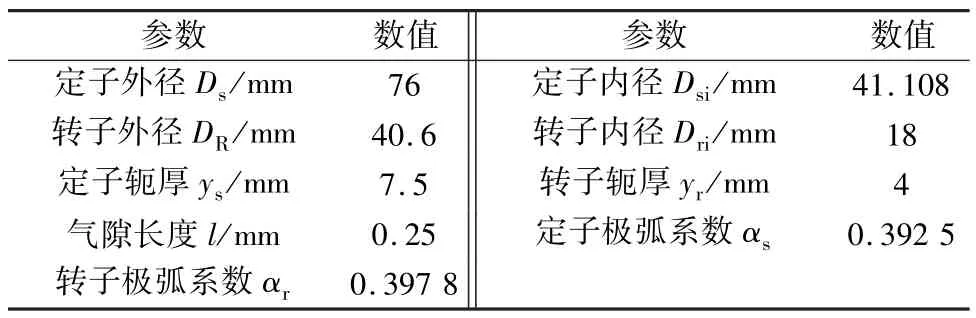
表1 样机的主要参数
(1)忽略由励磁磁极经定子极间空间到定子轭的漏磁通以及励磁磁极到相邻定子齿的漏磁通;
(2)忽略涡流效应;
(3)以定子外径圆和转子内径圆为边界,忽略其外的磁场和电机端部效应;
(4)在求解域内引入的矢量磁位在Az满足B=▽×A;
通过上述假设,可以推出SRM磁场的非线性方程和边界条件:

式中:Jz为电流密度,在非电流区Jz=0,μ0为选用硅钢片的磁导率。
图2(a)为常规定子结构在定转子未完全重叠区域的气隙磁力线分布图,图2(b)为开槽定子结构的分布图,两者的定转子重叠位置角相同,励磁电流也相同。可以看出,开槽方式增大了开槽区域相应的气隙磁阻,使得本应从该区域垂直进入转子齿的磁力线,朝着磁阻相对更小的(未开槽区域-气隙-转子齿)挤压,顺应地,未开槽区域磁力线被挤压到定转子非重叠区域。被挤压部分的磁力线由原来在重叠区域垂直进入转子齿变成在非重叠区域抛物线进入转子齿,将原本的径向磁通分解到径向和切向两个分量上。通过定子齿开槽结构,降低了定转子间的径向磁密,增大了切向磁密。
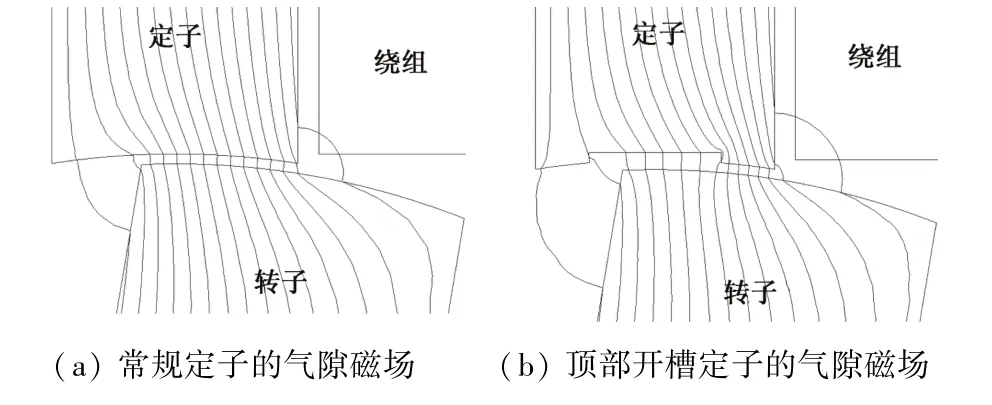
图2 磁力线分布对比图
3.2 瞬态场分析
在某时刻常规定子样机和开槽定子样机气隙磁密的径向分量和切向分量沿圆周方向的两个定子极距内的分布如图3所示,其中,开槽定子的开槽宽度为1 mm,开槽深度为0.2 mm。与常规定子相比,开槽定子的气隙径向磁密最大值下降了4.2%,切向磁密最大值增加了7.4%。
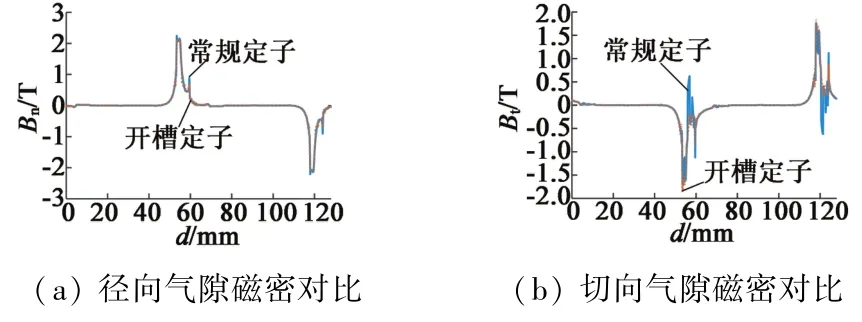
图3 常规定子与开槽定子的气隙磁密对比图
图4 为径向电磁力波形图。相比于常规定子,在开槽定子结构下,径向力波峰值下降了32.25%。
图5对常规定子和开槽定子的输出转矩进行对比。结果表明,相比于常规定子,开槽定子的平均转矩下降了1.43%;但是,转矩脉动降低了5.42%。
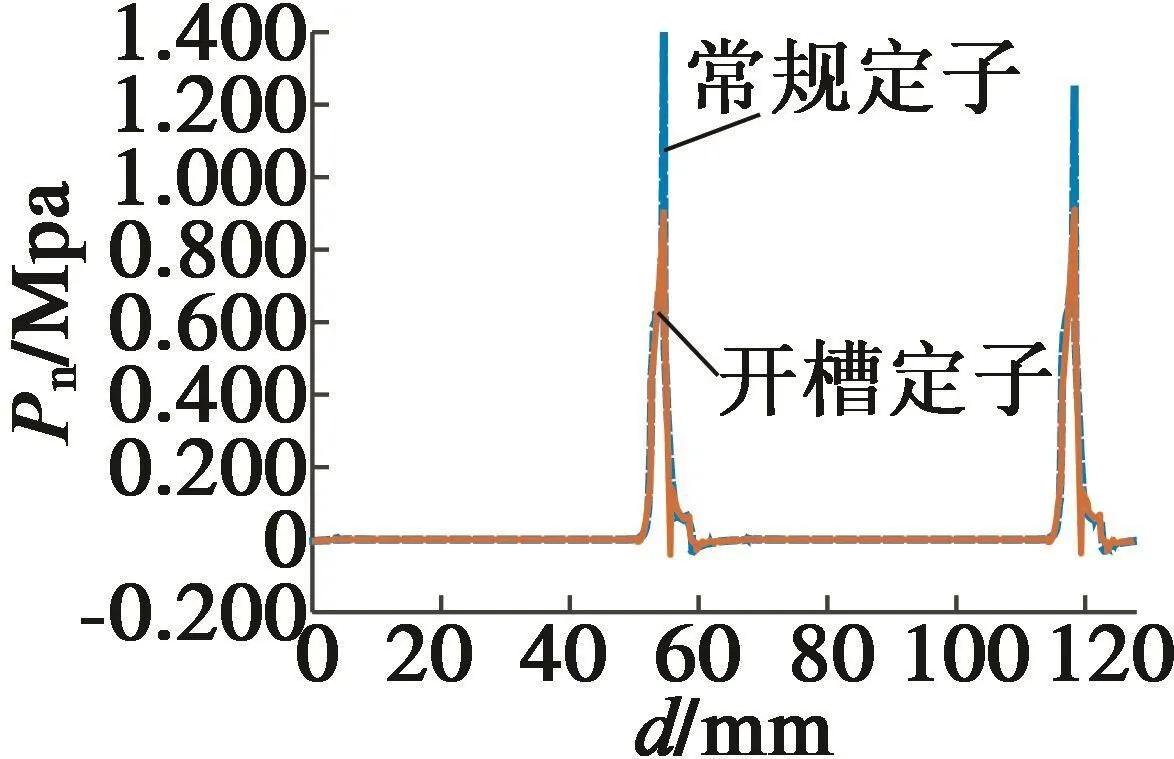
图4 径向电磁力波波形图

图5 转矩对比图
3.3 开槽大小对SRM影响
当开槽深度加深时,由于增大了气隙,降低了定转子重合部分的电感,进而降低了重合部分的径向力,但也同时更大程度地降低了转矩。文献[14]证明气隙厚度对转矩脉动的影响不是线性的,随着气隙厚度增大,转矩脉动先减小,当到达一定值后开始增大。所以定子表面开槽的关键应是开槽宽度,而非开槽深度。
保持开槽深度2 mm不变,将开槽宽度分别取为1 mm,2 mm和3 mm,对电机的转矩和径向力波进行瞬态仿真分析。
如图6所示,设置定子的开槽宽度a在1 mm,2 mm和3 mm时,相比于常规定子,其平均转矩分别下降了1.43%,4.38%和6.77%;转矩脉动分别下降了5.42%,3.78%和4.44%。
如图7所示,相对于常规定子,开槽宽度在1mm,2mm和3mm时,径向力波峰值分别下降了32.25%,37.12%和40.07%。
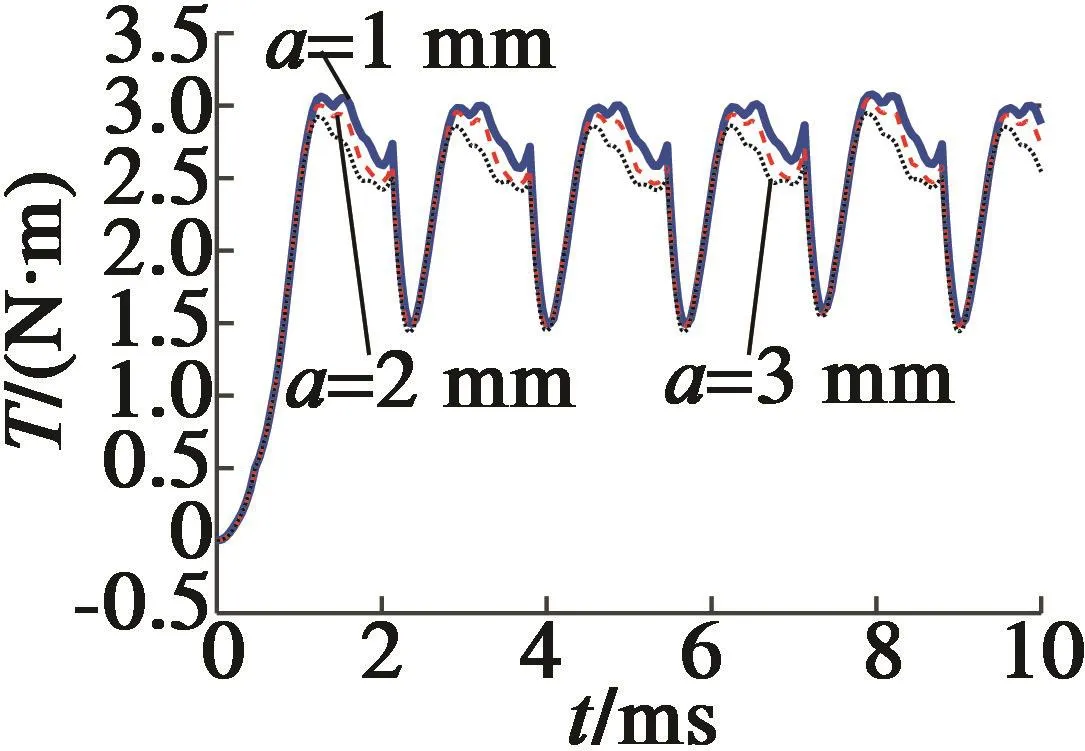
图6 不同开槽宽度a下的转矩
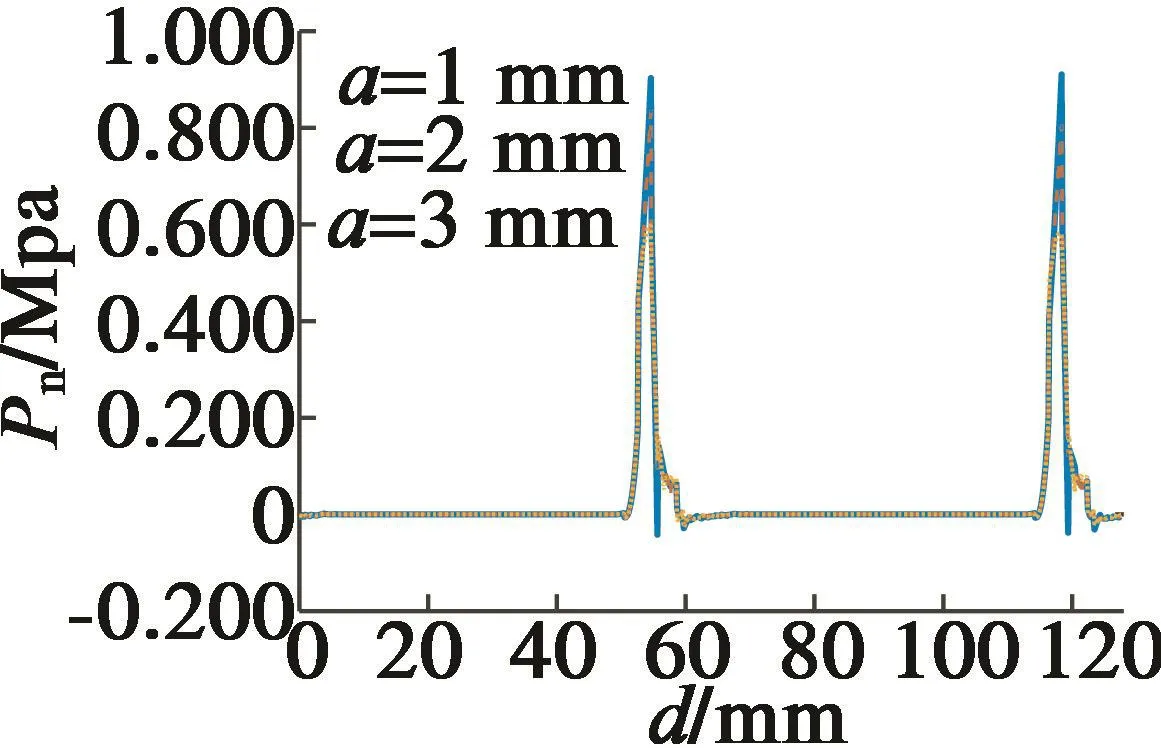
图7 不同开槽宽度a下的径向力
随着开槽宽度的增加,转矩逐渐下降,径向力波也逐渐下降。综合对比图6、图7数据,选定开槽宽度1 mm,深度2 mm为最优开槽尺寸,此时平均转矩下降了1.43%,径向力波峰值下降了32.25%,转矩脉动下降了5.42%,达到减小电机振动的目的。
4 定子轭结构
降低SRM振动的方法之一是尽可能提高电机定子部分的固有频率,包括改变定子轭和电机壳体几何形状等,以此避免SRM径向力波和定子固有频率一致时而产生的共振。如图8所示,在定子齿开槽基础上,将原来的圆形定子结构改为外接正8边形结构,所有定子齿都位于8条边的中间,此处的定子轭厚度不变,但增大了8边形角落部分的轭厚。这样有效地增大定子的固有频率,并降低了定子的振动位移[15]。
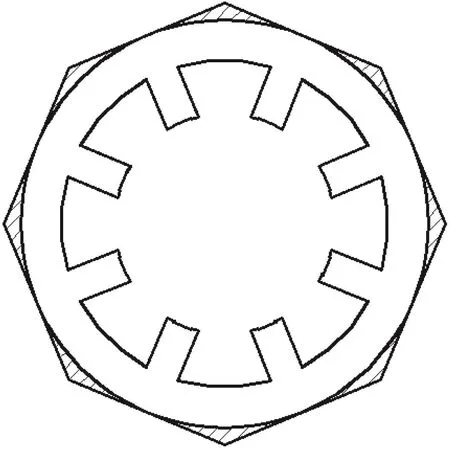
图8 增大定子轭厚的正8边形定子结构
定子材料采用50W470硅钢片,其弹性模量E=2.05×1011Pa,泊松比 M=0.27,密度 ρ=7 700 kg/m3。根据样机参数,对常规定子和正8边形定子做无约束的自由振动模态分析,结果如表2所示。可以看出,增大定子轭厚的正8边形开槽定子结构从1阶到6阶的固有频率都高于常规开槽定子结构。

表2 增大定子轭厚的开槽定子前后的振动模态
5 结 语
本文提出了一种在定子齿顶部开矩形槽的新型定子结构,经过有限元软件仿真分析可以得出如下结论:
1)与常规定子结构相比,开槽定子结构气隙径向磁密最大值降低了4.3%;切向磁密最大值增加了7.4%;径向力波峰值下降了32.25%;转矩脉动下降了5.42%。
2)通过定子开槽,定子齿对转子齿重叠区域的径向力部分转移为转子齿对定子槽方向非重叠区域的径向力,从而降低了造成电机振动的有效径向力。对电机转矩脉动进行对比,结果表明新型定子结构转矩脉动有明显改善。同时,将定子轭改为增大定子轭厚的正8边形定子,新结构有更小的振动位移和更高的固有频率。
