基于快速非奇异终端滑模的直线开关磁阻电机位置控制

周龙飞,赵世伟

(华南理工大学,广州510640)

0 引 言

直线驱动式电机在减少中间传动装置的同时提高了运行效率和控制精度,因此在精密直线运动的场合具有重要的地位。直线开关磁阻电机属于一种直线式机电能量转换装置,它将传统的旋转式开关磁阻电机和直线驱动式电机结合在一起,具备了两者的双重特点[1],使得该电机具有广阔的应用前景[2-3],尤其是在高精度伺服控制领域,得到了越来越多的关注。但同时它也存在电磁关系高度非线性、电磁力脉动较大、精确模型难以建立等缺点,因而使得该电机的控制方式较为复杂。

近年来,针对直线开关磁阻电机高性能伺服控制成为了中外学者研究的热点。传统PID在工业控制领域的应用较为常见[4],然而,直线开关磁阻电机的动态特性复杂,电机参数在运行过程中也可能发生变化,传统PID在复杂工况下的控制效果难以保证。文献[5]采用了多相激励以及平滑电磁力控制,有效地减小了电磁力脉动;文献[6]研究了PI控制和滞环电流控制,实现了电机的四象限运行;文献[7]基于自校正技术对直线开关磁阻电机进行了位置控制,克服了该电机模型不确定的缺点,且具有较高抗干扰能力;文献[8]研究了无源性控制算法在直线开关磁阻电机中的应用,增强了该电机控制性能和全局稳定性;文献[9]研究了协调跟踪控制和群控制在直线开关磁阻电机位置跟踪中的应用,减小了跟踪误差;文献[10]研究了滑模变结构控制在永磁同步电机控制系统中的应用,实现了给定指令信号较好的跟踪性能。

滑模变结构控制[11]发展初期主要研究线性滑模,滑动面表示为系统状态的线性函数。线性滑模面决定了系统状态以指数形式渐近收敛于给定轨迹,即表示系统状态不断趋近,但却永远无法到达给定轨迹。终端滑模[12]是一种有限时间收敛的滑模控制策略,通过将非线性项引入滑模面中,滑模面将跟随系统状态或者时间的改变而改变,从而改善系统的收敛特性,使得系统状态可以在有限时间内收敛至给定轨迹。

本文运用终端滑模控制中的快速非奇异终端滑模控制算法(以下简称FNTSM)[13]对直线开关磁阻电机位置控制器进行设计,并论证了系统的稳定性和收敛性。通过Simulink仿真,将其与传统的PID控制和基于指数趋近律的滑模控制(以下简称SMC)进行了对比分析。

1 直线开关磁阻电机结构和数学模型

1.1 直线开关磁阻电机结构

本文采用的直线开关磁阻电机结构模型如图1所示,为双凸极铁心结构,主要由定子导轨和动子两部分组成。图中:x0=40 mm,x1=40 mm,x2=10 mm,x3=18 mm,y1=5 mm,y2=12 mm,z=0.55 mm,d=12 mm。

图1 直线开关磁阻电机结构图

1.2 直线开关磁阻电机数学模型

直线开关磁阻电机的各绕组的磁路相互独立,可以忽略各相绕组之间互感,因此可以分别列写各相绕组的电压平衡方程如下:

式中:ek,Rk,ik,Uk,ψk分别为相绕组感应电动势、电阻、电流、外加电压和磁链,其中k=a,b,c。由于绕组磁链是相电流ik和位移x的函数,故可得如下形式的电压平衡方程:

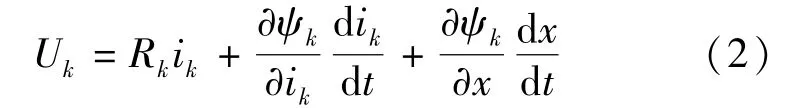
该电机的电磁力fe可根据机电能量转换原理推导得到:

该电机的机械运动方程:

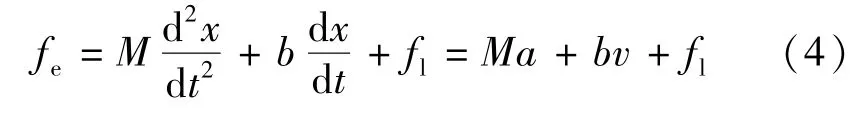
式中:M,b,fl,a,v分别为动子质量、摩擦系数、负载、动子运动加速度、动子运动速度。

当该电机的磁路工作在线型状态时,各相绕组磁链仅为位移的函数,所以其电磁力可以表示:

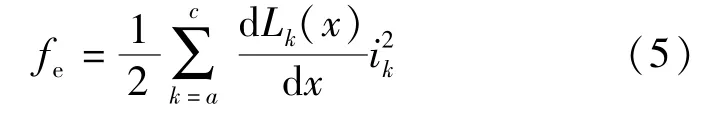
为了提高电机的工作性能,常常使该类电机工作在磁路饱和区间。本文对该直线电机进行了有限元建模及仿真分析,得到该电机的磁化特性曲线和电磁力特性曲线分别如图2和图3所示。

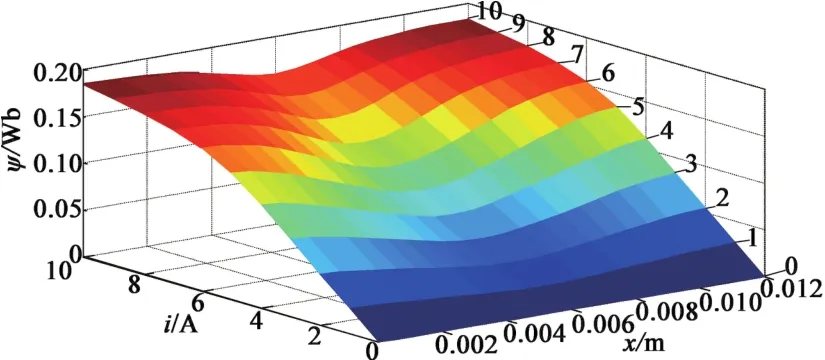
图2 电机非线性磁化曲线

图3 电机电磁力特性

由图2、图3可知,该电机的磁化特性和电磁力特性均呈现较强的非线性特点,难以精确建立此种电机的数学模型。为了保证仿真精度和简化建模工作,本文采用查表法[14]对该电机的磁化特性及电磁力特性进行仿真建模。

2 控制器设计

2.1 控制系统结构框图

控制系统的结构框图如图4所示。系统采用双环级联结构,内环为电流环,外环为位置环。一般来讲,由于电机的电磁时间常数远小于其机械时间常数,故可以认为机电系统是由电磁快变子系统和机械慢变子系统组成。从两时间尺度的角度理解,可以分别针对内环和外环独立设计控制器,从而简化该系统控制器设计过程。为了提高电流响应速度及简化计算,本文的电流控制器采用比例控制算法,位置控制器分别采用PID算法、基于指数趋近律的滑模控制算法以及快速非奇异终端滑模控制算法。

图4 直线开关磁阻电机位置控制框图

由图4可以看出,控制过程为将位置指令与实际位置x的差值输入位置控制器得到电磁力指令,进而根据力分配函数表得到三相力指令三相力指令通过有限元数据查表得到三相电流指令最后通过三相电流控制器得到三相控制指令,即各相绕组输出电压。

2.2 力分配函数

为了使电机获得期望电磁力,电机的绕组励磁应与电机的运行位置进行同步切换。直线开关磁阻电机有单相和多相导通运行方式,本文采用多相绕组交错导通励磁方式[14],以减少电机电磁力脉动。具体实现方式是以一个齿和槽的距离(y2=12 mm)作为励磁周期,将其划分为6个区间,根据不同区间的相对位移和电磁力指令来分配各相绕组所应贡献的电磁力大小,以此来减小电机运动过程中所产生的电磁力波动。力分配函数如表1所示[7,14]。其中为控制器输出的期望力指令。

表1 力分配函数表

2.3 快速非奇异终端滑模控制器设计

一般滑模控制系统的运动过程包含趋近运动和滑模运动两个阶段。在趋近阶段,滑模控制推动系统状态向滑动面运动。当系统状态到达滑模面时,系统运动由趋近阶段转为滑动模态,系统状态降阶表示为滑模面的方程。

由式(4)可得如下系统的状态空间表达式:

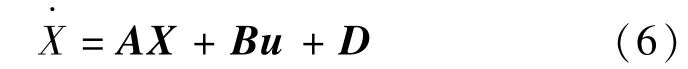
式中:

根据式(6)可得:

式中:kc为库伦摩擦力系数;sgn()为符号函数。

根据快速非奇异终端滑模的定义,在传统的线性切换函数中引入非线形项。设位置指令为xref,定义位置误差为误差变化率为则切换函数的表达式:

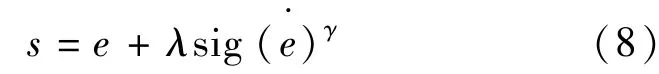
式中且均为正奇数)由的定义可知,此函数为光滑连续且单调递增的,并且返回值为实数。

常用的滑模控制律的设计方法为滑模等效控制方法[15],控制律通常包含等效控制项和切换控制项两部分。故将控制律设计为如下形式:

式中:ueq为等效控制项,un为非线性控制项。下面详细给出控制律设计过程。

为保证滑动模态的存在,暂且不考虑系统的参数摄动和外部扰动,对s求时间的一阶导数得:

1)当时:

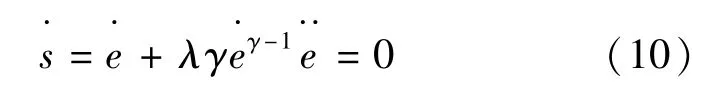
将式(7)代入,并假设fl=0,得到:

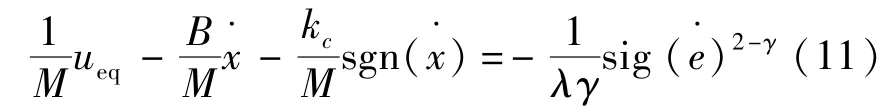
从而得到等效控制律:

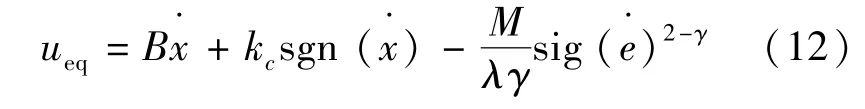
式中:1<γ<2,故从理论上保证了控制器不存在奇异控制区域。

2)当时,根据且p,q均为正奇数,可得到与式(12)相同的等效控制律。同时,将非线性控制项设计:

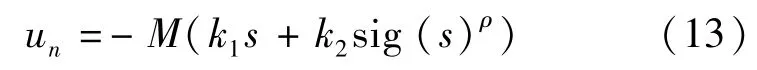
式中:k1,k2为常数,0<ρ<1。

综上可得快速非奇异终端滑模控制器的控制律:

根据上述控制器设计过程,影响控制器输出的参数主要是λ,γ,ρ。通过对切换函数和控制律的分析可知:较小的λ会使得系统具有更大的带宽,也就意味着更快的响应速度和更高的跟踪精度;增大γ值可以有效地缩短收敛时间,但同时也会放大系统的测量误差;在满足0<ρ<1的条件下选择较大的ρ值可以得到更加光滑的控制信号,因而有效地削弱控制器信号的抖振,但会降低系统的鲁棒性。总之,选择合适的控制器参数对控制系统的性能至关重要。

2.4 控制器特性分析

2.4.1稳定性分析

对于上述快速非奇异终端滑模控制器,构建Lyapunov能量函数其中V≥0,当且仅当s=0时V=0。对V求一阶导数,并将式(14)代入整理可得:

式中

根据上式中参数的取值可知:ψ1>0,ψ2>0,故0,当且仅当s=0时,=0。因此表明该控制系统将由初始状态收敛于滑模面,系统是全局稳定的。

2.4.2收敛性分析

根据上述稳定性分析可知,该系统在给定的控制律作用下收敛于滑模面。当系统状态到达滑动面时,系统运动由趋近阶段转为滑动模态,即从到达滑模面的初始状态收敛于误差坐标的原点。

当e≠0,≠0的情况下,则存在实数ε1>0,ε2>0,满足ψ1≥ε1,ψ2≥ε2,由式(15)可得:

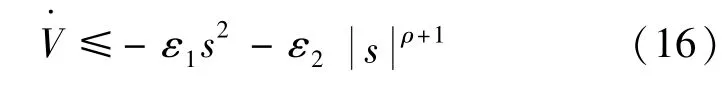
将函数代入式(16)可得:

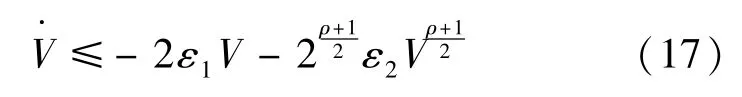
根据文献[15]求解上述不等式,可得系统状态收敛于误差坐标原点的时间tr:

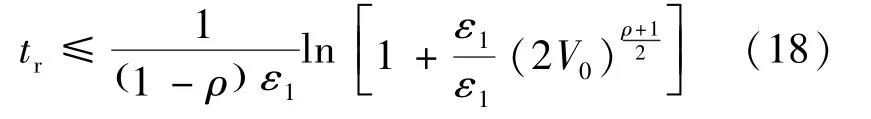
式中:V0=V[s(0)],即系统的初始状态。

上式表明在给定系统初始状态的情况下,控制系统的跟踪误差将在有限时间内收敛于误差坐标原点,即

通过对FNTSM位置控制器的设计以及对控制器特性的分析,可见该控制器有效地避免了奇异点的出现,而且在控制律中引入指数项,使得系统有较快的收敛率,提高了系统的响应速度。同时,还利用连续函数代替在滑模变结构控制律中使用的开关函数,使控制律的连续性得到了实现,这样可以有效地削弱控制信号的抖振,能够让系统的稳定性进一步提高。

3 控制系统仿真结果与分析

本文采用上述直线开关磁阻电机数学模型以及快速非奇异终端滑模算法在Simulink环境下仿真,并分别与传统PID控制和基于指数趋近律的SMC控制的仿真结果进行了对比分析。

仿真中所用电机模型主要参数:对齐位置电感Lal=21.9 mH,非对齐位置电感Lua=17.9 mH,摩擦系数B=0.08,动子质量M=2 kg,给定跟踪位置指令为±0.1 m的方波。

仿真结果表明,直线开关磁阻电机仿真模型在传统的PID控制器和FNTSM控制器下均能够准确地跟踪方波位置信号。图5表示PID控制器和FNTSM控制器具有相同的响应速度,从图中可知两种控制方式下的上升时间约为0.3 s,但相对于FNTSM控制算法,采用PID控制使得该位置控制系统具有明显的超调。虽然保证了较快的响应速度,但在高精度的位置控制中超调是不允许的。图6为适当减小PID控制器中的比例参数,并略微增大微分系数后得到的仿真结果。此时两种控制器均实现无超调跟踪,但此时PID控制器的上升时间明显较长,达到0.5 s。图7是控制系统运用两种控制算法时的位置跟踪误差,所得到的稳态误差分别为30 μm(FNTSM)和180 μm(PID)。

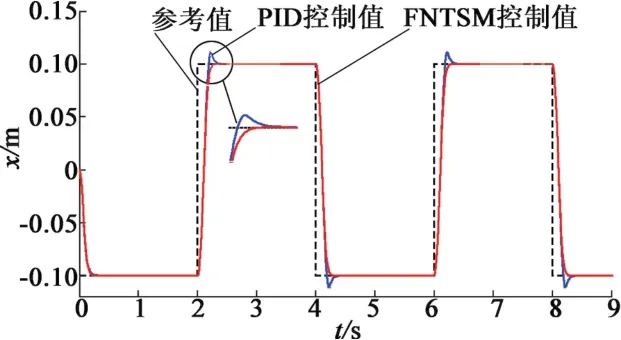
图5 FNTSM和PID位置跟踪曲线仿真图

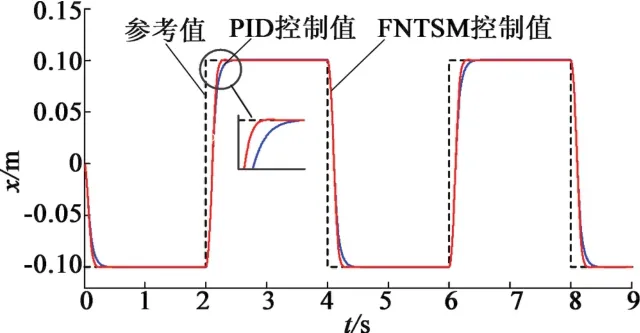
图6 FNTSM和PID位置跟踪曲线仿真图

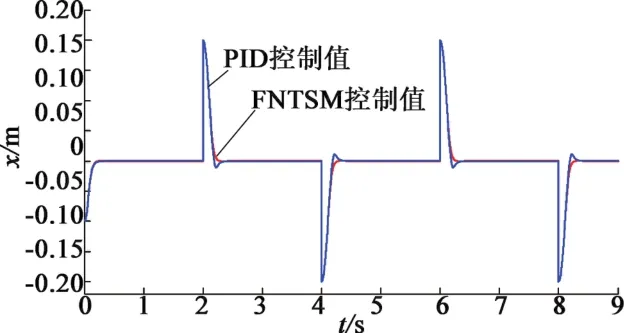
图7 位置跟踪误差仿真图

通过上述分析说明直线开关磁阻电机快速非奇异终端滑模位置控制在保证系统稳定运行的前提下,相较于传统PID控制具有更好的动态性能和更小的稳态误差。

图8为FNTSM和SMC控制器仿真结果。表明基于指数趋近律的传统滑模控制(SMC)和本文应用的FNTSM控制算法的动态过程无明显差别,但FNTSM的上升时间更短,响应速度更快。而且电机模型在两种控制器下的稳态跟踪误差也没有明显差别,满足高精度伺服控制的要求。基于FNTSM算法的控制器输出和基于指数趋近律的SMC算法的控制器输出分别如图9和图10所示。通过对比可知,在系统状态接近平衡点附近时SMC控制器有明显地高频抖振。而FNTSM控制器通过选择非线性滑模面和在控制律中有目的更换传统的切换函数,可以明显地削弱系统状态在滑模面上的高频抖振,保证系统状态在有限时间内收敛于误差坐标原点,实现对给定轨迹的准确跟踪,提高了系统的响应速度和稳定性。

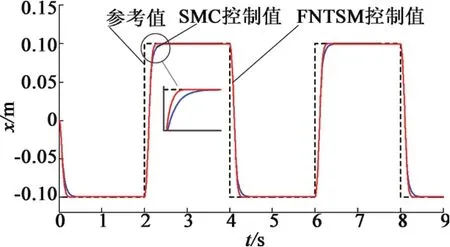
图8 FNTSM和SMC位置跟踪曲线仿真图

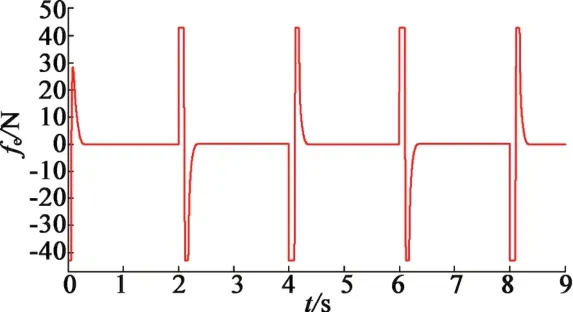
图9 FNTSM控制器指令输出仿真图

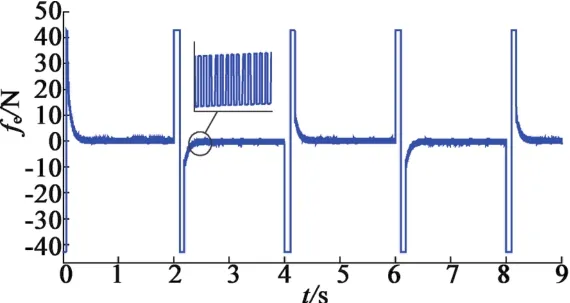
图10 SMC控制器指令输出仿真图

4 结 语

本文采用快速非奇异终端滑模控制算法对直线开关磁阻电机进行了位置控制器的相关设计,并在Simulink中搭建仿真模型进行算法验证。通过将仿真结果分别与传统PID控制器和基于指数趋近律的SMC控制器的仿真结果对比分析后可知,在FNTSM控制下电机位置误差能够更快地收敛至平衡点,而且具有无超调,平衡点附近波动小,控制量抖振小,稳态精度高等特点。因此,该算法在工程中具有广泛的应用前景。

参考文献

[1] Wai Chuen Gan,Cheung.N.C.Design of a linear switched reluctance motor for high precision applications[C]//2001 International Conference on Electric Machines and Drives,2001:701-704.

[2] 吴南星,孙庆鸿.直线电机与高速精密数控机床进给系统的研究[J].制造业自动化,2003,25(10):46-48.

[3] 李绪成.直线电机在数控机床中的应用及发展趋势[J].世界制造技术与装备市场,2005(6):71-74.

[4] 林旅,曹广忠,潘剑飞,等.基于TMS320F2812的直线开关磁阻电机位置控制系统研究[J].微电机,2009,42(7):36-39.

[5] BAE H K,LEE B S,VIJAYRAGHAVAN P,et al.A linear switched reluctance motor:converter and control[J].IEEE Transactions on Industrial Applications,2000,36(5):1351-1359.

[6] DORNINGOS J L,ANDRADE D A,FREITAS M A A,et al.A new drive strategy for a linear switched reluctance motor[C]//Electric Machines and Drives Conference,2003(3):1714-1719.

[7] 杨金明,赵世伟,钟庆,等.基于自校正技术的开关磁阻直线电动机的位置控制[J].中国电机工程学报,2008,28(6):99-103.

[8] ZHAO S W,LUO L N,YANG L Q,et al.High precision position control of linear switched reluctance motor for short distance[C]//International Conference on Power Electronics Systems and Applications,2002:37-42.

[9] ZHANG Bo,YUAN Jianping,QIU Li,et al.Distributed coordinated motion tracking of the linear switched reluctance machine-based group control system[C]//IEEE Transactions on Power Electronics,2016,63(3):1480-1489.

[10] ZHANG X,SUN L,ZHAO K,et al.Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J].IEEE Transactions on Power Electronics,2013,28(3):1358-1365.

[11] UTKIN V I.Variable structure systems with sliding modes[J].IEEE Transactions Automatic Control,1977,22(2):212-222.

[12] 王艳敏.柔性机械手非奇异终端滑模控制方法的研究[D].哈尔滨:哈尔滨工业大学,2009.

[13] ZHENG J,WANG H,MAN Z,et al.Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode[J].IEEE/ASME Transactions on Mechatronics,2015,20(4):1743-1752.

[14] GAN W C,NORBERT C,QIU Li.Position control of linear switched reluctance motors for high-precision applications[J].IEEE Transactions on Industrial Applications,2003,39(5):1350-1361.

[15] FENG Y,YU X,MAN Z.Non-singular terminal sliding control of rigid manipulators[J].Automatica,2002,38(12):2159-2167.

[16] YU Shuanghe,YU Xinghuo,STONIER R.Continuous finite-time control for robotic manipulators with terminal sliding modes[C]//Sixth International Conference of Information Fusion,Cairns,Queensland,Australia,2003:1433-1440.