四悬臂复合换能器式圆筒行波超声波电动机的研究
2017-05-15赵学涛孙砚飞李兆胜
刘 荣,赵学涛,孙砚飞,李兆胜,陈 晨
(山东理工大学,淄博255049)
0 引 言
超声波电动机是20世纪80年代迅速发展起来的一种新型电机,是一种基于压电效应和超声振动的高新技术电机[1-2]。超声波电动机拥有大转矩、转速低、灵活设计、结构简易、断电自锁、响应速度比较快和没有电磁干扰等特征[3-4]。为了适应空间的各种机构和对各种机械零部件对动力的要求,提高电机的的输出性能是现在的当务之急。因此我们可以将重点放在悬臂式超声波电动机上[5-7]。而悬臂式超声波电动机通过采用d33耦合系数,极大地提高了电机的运转速度。并通过紧固螺栓给予悬臂一定的预紧力,确保压电陶瓷的工作状态在压应力作用下,以便使其通过高频电压激励,达到显著提升了电机的输出性能的目的[8]。基于悬臂换能器的优点,本文提出了一种四悬臂梁纵弯复合换能器式圆筒行波超声波电动机,通过对换能器纵振和弯振的复合实现转子的转动。采用有限元方法对其结构进行模态分析和瞬态分析,并对电机进行设计和仿真。
1 电机的结构和原理
1.1 电机驱动器的结构

图1 驱动器的主体结构
本文主要是针对驱动器的设计,输出轴根据所设计驱动器进行选用。图1为驱动器的主体结构设计。该驱动器是由一个圆筒和4个悬臂纵弯复合式换能器构成,换能器位于圆筒的外侧。换能器的结构则是由两个端盖、螺栓、悬臂梁、电极片,一组纵振压电陶瓷片和两组弯振压电陶瓷片构成。纵振陶瓷片中间设计有圆孔,一组纵振陶瓷片位于两个悬臂梁之间,而两组弯振陶瓷片分别位于悬臂梁外侧,悬臂、纵振压电陶瓷片、弯振压电陶瓷片和端盖通过一螺栓配合紧固成一体构成一个换能器。在相邻的弯振陶瓷片之间、相邻的纵振陶瓷片之间、弯振陶瓷片和悬臂之间以及纵振陶瓷片和悬壁之间均设计有电极片。由于电极片非常薄,设计时厚度可以忽略。而相邻的纵振压电陶瓷和弯振压电陶瓷的极化方向相反[9],弯振压电陶瓷是由一个完整的压电陶瓷圆片从中间割成半片。A和B分别代表不同的电极,电极片加入与设计电机匹配的电压。陶瓷的摆放位置如图2所示。
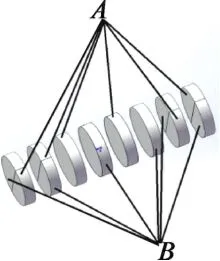
图2 压电陶瓷的摆放位置
1.2 电动机的驱动原理
换能器的运行原理是依据波动理论,只需在圆筒上激励出两列频率相等、幅值相等,在时间和空间上相位差为π/2的弯曲振动驻波就可以激励出弯曲振动的行波。
A相驱动激发的驻波:B相驱动激发的驻波:


两列驻波叠加:

当电压陶瓷对称极化时相激励电压的相位差在时间上相差90°,则θ=π/2,有:

式(1)~式(5)中,ωA,ωB为横向位移;xa为A相和B相空间间隔;ξA,ξB分别为横向振幅;k=2π/λ为振动的波数;λ=L/n为波长;n为振动阶数;L=2πr为圆筒周长;r为圆筒平均半径;θ为A相和B相驱动的相位差[10]。
由式(1)~式(5)可得,只要两相驱动电压相位差为π/2,即能形成行波。
本文设计的电动机则分别通过4个换能器中的纵振压电陶瓷激励出换能器的纵振,同时用弯振压电陶瓷片激励换能器的弯振,通过和圆筒的相互作用,在圆筒中分别激励出一列弯振驻波和一列纵振驻波,电机工作时所加电压的相位差相差π/2,这样就可以在圆筒中激励出一列行波。
2 电动机的有限元分析
2.1 对换能器进行模态分析和设计
换能器的组合宽度对定子的动态特性影响比较显著,其可以直接影响到模态幅值大小和模态频率。换能器厚度越大,定子的刚度增加,相同阶次的模态频率增高,为防止模态频率增高,换能器不宜过厚。综上,首先给定一个初始尺寸参数,用SolidWorks做出初始图导入Ansys WorkBench做模态分析。分析采用不加约束的自由模态,由于胶层和电极片的厚度很小,分析过程中不予考虑,并采用直接法(Direct)进行求解。所得的悬臂梁换能器的一阶纵振和二阶弯振的模态振型和频率如图3、图4所示。

图3 换能器的一阶纵振特征
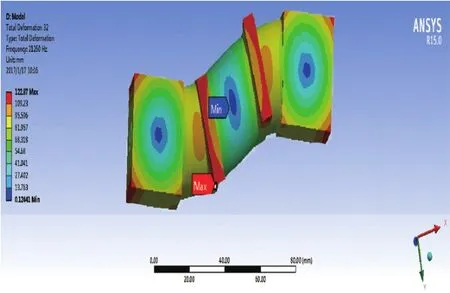
图4 换能器的二阶弯振特征
当端盖长为18 mm,宽21 mm,高为21 mm时,可以得到模态分析的一阶纵振频率为21 183 Hz,二阶弯振频率为21 260 Hz,其频率差小于0.5%,实现了良好的简并。
2.2 圆筒的模态分析和设计
圆筒的内径过小,会使得更多能量传递到定子内部的内支撑板上而消耗;若内径过大,圆筒就比较窄,超声波电动机的输出功率也相应较小,同时圆筒的固定也会遇到困难。同时,根据质点的切向速度公式:

通过式(6)知道,使定子齿增高会使定子表面质点的周向振幅增高,从而达到提高转速的目的。但是,齿太高,又会使得输出扭矩有一定下降,在接触区域内,定子质点沿周向速度变化更大,会降低超声波电动机的输出效率。圆筒驱动齿齿槽宽越小,越能提高超声波电动机的平稳性。同时,齿槽宽减小,还使得圆筒和转子的接触面积增大,有利于提高输出性能。但齿槽宽不能小于0.3 mm,这样加工会困难。圆筒材料为铝合金,其各项机械性能如表1所示。得到圆筒的尺寸圆筒直径90 mm,壁厚5 mm,齿高4 mm,齿槽宽1.64 mm。根据上述分析,为使圆筒的频率与换能器的频率实现一致(频率简并),对定子圆筒进行基于有限元的分析设计。圆筒的六阶径向弯振如图5所示。

表1 定子结构尺寸

图5 定子的六阶径向弯振特征(截图)
分析后得到圆筒的频率为21 468 Hz,与换能器的最大频率差不超过200 Hz,低于简并频率1%,能够与换能器的纵弯模态实现较好的简并。
2.3 电机的模态分析
将装配体导入进行模态分析,由于电机的整体刚度增加,会出现模态频率不简并的现象,通过微调圆筒和端盖大小,减小共振频率,从而得到一阶纵振激发的六阶径向纵振模态和二阶弯振激发的圆筒六阶径向弯振模态,如图6所示。
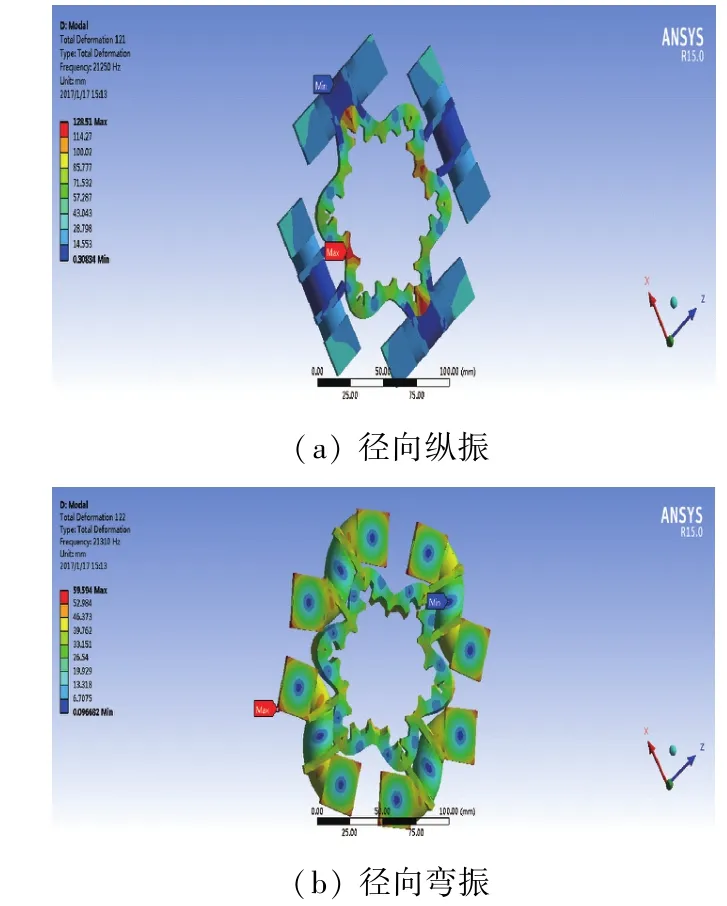
图6 六阶模态特征
分别得到一阶纵振激发的六阶径向纵振模态频率为21 250 Hz,二阶弯振激发的六阶径向弯振模态频率为21 310 Hz,两种模态频率相差60 Hz,低于简并频率的0.5%,说明两种模态实现了良好的兼并。最后得到调整后的电机各项参数尺寸见表1。
2.4 电机的瞬态分析
在Workbench中安装ACT-Piezo的压电分析模块,选取其中一个换能器进行谐响应分析,本设计采用的压电陶瓷为PZT-4,压电分析时参数设置如图7所示。
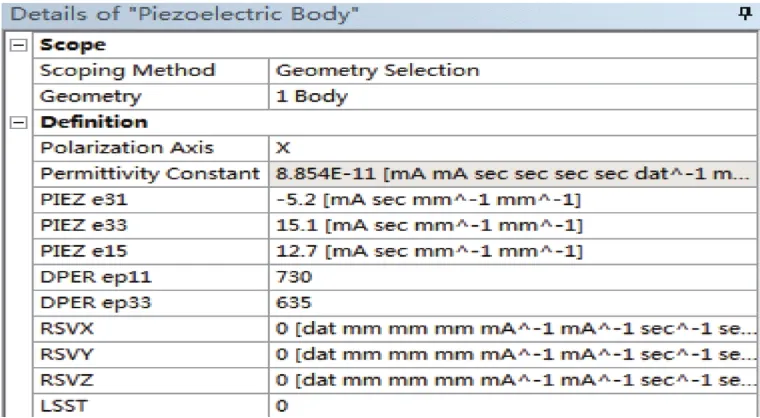
图7 压电分析参数设置(截图)
选取其中一个换能器,对其纵振压电陶瓷加载均值为100 V交变电压激励,频率响应范围为21 200~21 300 Hz之间,分析响应频率点数为25,采用完全处理法(full)。完全处理法虽然处理速度较慢,但是可以得到更加细化的分析结果。通过分析得到换能器在21 288 Hz时振动位移最大,此时发生共振,如图8所示。

图8 悬臂质点的谐响应分析
选取xoy的平面,提取悬臂与圆筒接触的一个质点作为研究对象,对其进行简谐振动测试。根据实际工况,对压电陶瓷片施加同一频率和振幅,相位差为频率为ω=2πf,运动形式为的简谐运动,进行瞬态分析,如图9所示。最小时间为t=1/(20f),f=21 288 Hz,步数为1,结束时间为0.002 s。
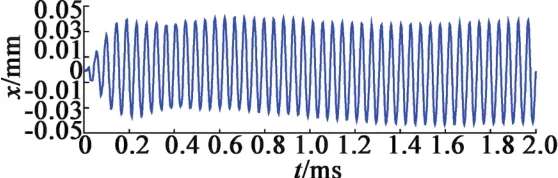
图9 质点x的瞬态分析
提取其中的300个点,用MATLAB做出轨迹图,如图10所示。
当只有一个换能器激励圆筒时,质点的最大位移为1.3 μm。而多换能器激励圆筒时,质点的最大位移为4 μm,振幅增加3倍。

图10 质点在xoy面上的运动轨迹
通过分析质点的运动可以看出,在xoy面上质点的运动轨迹都近似于椭圆。通过悬臂换能器的纵弯复合振动激励在驱动齿位置处合成较近似椭圆运动的轨迹,从而通过摩擦耦合驱动转子运动,验证了设计的正确性。
3 样机及实验
根据表1给出的电机结构参数,研制了四悬臂纵弯复合换能器式圆筒型行波超声波电动机样机,如图11所示。

图11 四悬臂纵弯复合换能器圆筒行波超声波电动机样机
将悬臂式超声波电动机的输出能力进行相关实验,取VL(rms)=70 V,VB(rms)=200 V,两相激励电压之间相位差为π/2,定转子之间预压力为5 N。图12为样机在频域内空载情况下的转速曲线。测试结果表明:电机的最佳工作频率为21 290 Hz。图13为样机的转速与力矩关系曲线。输出特性测试结果表明,悬臂纵弯复合换能器式圆筒型行波超声波电动机样机最大转速为191 r/min,最大输出力矩为0.90 N·m。该电机与单悬臂纵弯合换能器式圆筒行波超声波电动机相比,在最大转速以及最大输出力矩均出现了明显的上升。

图12 电机转速与频率关系曲线

图13 转速与力矩关系曲线
4 结 语
本文设计了一种新的圆筒行波超声波电动机,并分析了其工作原理进而验证了其可行性。
合理的使用有限元分析法,设计并分析了驱动器的悬臂梁换能器和圆筒,实现了悬臂梁和圆筒之间的模态简并,并确定了圆筒和换能器的最终尺寸,通过谐响应分析得出电机定子驱动器在22 188 Hz处位移达到最大值,有较好的共振。
通过对定子驱动器上的质点进行瞬态分析,定子通过齿轮的摩擦耦合驱动圆筒中的驱动轴转动,样机输出结果:最大驱动轴转速为191 r/min,最大驱动轴的力矩输出为0.9 N·m。
参考文献
[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007:1-10.
[2] 刘英想,姚郁,陈维山,等.纵振复合双足直线超声电机[J].西安交通大学学报,2012,46(8):112-115.
[3] POZAR D M.微波工程[M].张肇仪,周乐柱,吴德明等译.3版.北京:电子工业出版社,2008:442-447.
[4] 张楠,冯宇波.PIN二极管在射频开关电路中的工作原理及应用[J].科技信息:学术版,2007(2):10-14.
[5] LU L Y,WANG C H,ZHANG B X.Timek-frequencey analysis of the dispersive Rayleigh wave in stratified media[J].Chinese Journalof Acoustics.2006,25(4):297-309..
[6] LIU Y X,CHEN W S,LIU J K,et al.A cylindrical traveling wave ultrasonic motor using longitudinal and bending composite transducer[J].Proceeding of the Case,2010,161(1-2):158-163.
[7] 苏松飞,姚志远,王长茹,等.一种弯曲模态直线超声的研究[J].压电与声光,2012,34(3):400-403.
[8] 胡百振,李有光,赵淳生,姚志远,等.新型纵弯超声电机振子的设计与分析[J].压电与声光,2014,36(3):353-354.
[9] 刘英想.纵弯模态超声电机理论与实验研究[J].机械工程学报,2013,49(4):82-83.
[10] 胡敏强,金龙,顾鞠平.超声波电机原理与设计[M],北京:科学出版社,2005.
