隔膜泵用磁致伸缩致动器的设计与实验研究
2017-05-15芮骥才谢荣建王仕越董德平
芮骥才,谢荣建,王仕越,张 添,董德平
(1.中国科学院上海技术物理研究所,上海200083;2.中国科学院大学,北京100039)
0 引 言
以磁晶各向异性补偿合金TbxDy1-xFe2为代表的超磁致伸缩材料(以下简称GMM)在交变磁场中可发生周期性的应变,实现电磁能-机械能的转换,GMM在室温下的饱和应变值可高达1 500~2 000 ppm,同时具有响应速度快(μs级别)、能量密度高、输出力大等特点,因此在微型动作元件以及流体机械中有着极强的应用优势[1-2]。
磁致伸缩致动器是通过给GMM施加合适的交变磁场使其产生预期的位移或力的输出的机构,本文介绍的致动器以隔膜泵作为负载,通过导杆将材料的振动传递至金属隔膜从而实现驱动,设计时考虑轭铁材料的真实物性,对整个致动器进行了有限元仿真,比较不同结构参数下的磁场分布,以形状因数作判据选取最优值,从而实现较高的驱动效率。
1 超磁致伸缩致动器的理论分析
1.1 超磁致伸缩材料工作特性
超磁致材料的工作特性由磁致伸缩方程式(1)、式(2)表示,其应变由应力场、磁场与温度场的共同作用引起[3]:

式中:ε为材料的应变;s为超磁致伸缩材料的柔顺系数;σ为内部应力;d为磁致伸缩应变系数;Hav为平均磁场强度;α为热膨胀系数;ΔT为材料的平均温度变化;B为磁感应强度;μ为材料的磁导率。
典型的磁致应变如图1所示。偏置压力与磁场强度对材料的变形量影响很大,合适的偏置压力会让材料有更大的应变,机电耦合系数更高。同时无论磁场方向正负,磁致应变均为正值,直接导致材料工作在交变磁场中会产生“倍频现象”,通常加入偏置磁体或直接由线圈提供偏置磁场使材料工作于线性工作区,从而避免该现象发生。

图1 不同压力偏置下磁致伸缩曲线
1.2 磁致伸缩隔膜泵
隔膜泵属于容积式泵,通过活塞或者隔膜的往复运动引起泵腔内部容积变化同时配合单向阀门完成流体的吸入与排出。与常规的旋转动力泵的不同在于,其流量输出相对比较稳定,同时在压缩比较大的情况下具有较强的自吸能力与抗气泡能力[4-6]。

图2 磁致伸缩隔膜泵结构示意图
本文介绍的磁致伸缩膈膜泵工作于流体传热回路,通过泵送低温流体工质通过换热器来冷却高温部件,其结构简图如图2所示。线圈内部通交流电产生交变磁场,超磁致材料棒在磁场中产生周期形变,通过导杆推动金属隔膜往复运动完成吸入和排出冲程,进出口均植入单向阀门确保流动方向一致。泵体设计频率为50 Hz,设计流量为1.8 mL/s,需要超磁致材料提供0.1 mm以上的峰峰值位移输出,同时导杆结构在传递位移的同时起到减少漏热的作用。
1.3 致动器磁路结构设计
由图2的结构可以看出,对于提供驱动磁场的线圈来讲,其主要参数为内半径a1,外半径a2,以及长度L,设计思路是在不超过一定的外径时,存在一个最优的参数搭配使GMM棒材磁场达到80 kA/m时系统的发热量最低。为描述该线圈的效率定义形状因数

同时对于均匀密绕的线圈,其铜损:

因此:
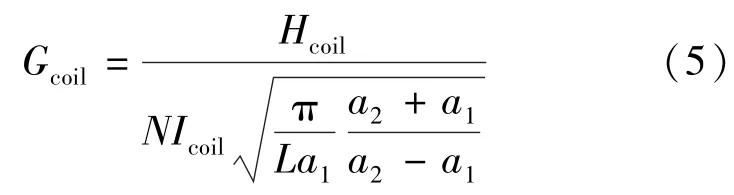
式中:Hcoil为线圈轴线中心磁场强度;λ为导线的填充因数,对于圆形截面的密绕导线一般取值π/4;pcoilloses为线圈铜损;ρ为导线电阻率;N为线圈匝数;Icoil为线圈内电流。
根据式(5)可知,在相同的安匝数NIcoil输入下,最优的线圈应该具有最大的磁场强度Hcoil。对于带轭铁的致动器,其磁力线分布与在空气中区别很大,而且由于材料磁导率的非线性,其中心场强Hcoil并不具有解析解,因此采用有限元软件MAXWELL对整个致动器进行建模,并通过参数化分析来寻找几何结构的最优值。
2 有限元分析
致动器的主要组成部分均为轴对称回转体,考虑到磁致应变上限约为总长度1‰,该形变量相对于其余部件尺寸来讲非常小,因此将整个致动器视为静态,求解器设置为轴对称稳态问题,采用二维柱坐标系建模,超磁致棒材与两端顶头以及外围轭铁构成封闭磁路包围线圈,磁轭材料均为电工纯铁,牌号为DT4E。系统关键参数如表1所示。

表1 系统关键参数
超磁致棒材的形状是固定的,线圈的内径和长度必须不小于棒材,其3个形状参数(a1,δ,h)取值与步长见表1,边界条件设置为气球边界,非结构网格的最小长度设置为0.2 mm,网格划分如图3所示。

图3 致动器网格划分
对于每一组参数均求解出收敛后的磁场分布,图4为a1,δ分别为8 mm和25 mm时的磁场分布。由图4可见,仅仅在轭铁接触处和拐角边界,磁感应强度的值达到最大值,接近1 T,低于电工纯铁的饱和磁密度,在磁路外部分B值较小,即轭铁起到了很好的磁屏蔽作用;同时封闭的轭铁磁路结构使磁力线聚拢到棒材内部,有利于在其中产生更强的磁场。取棒材中心磁场强度为Hcoil,代入到式(5)中计算当前的形状因数Gcoil,并且作出云图,自变量分别为a1,δ,如图5所示。在一定范围内形状因数Gcoil
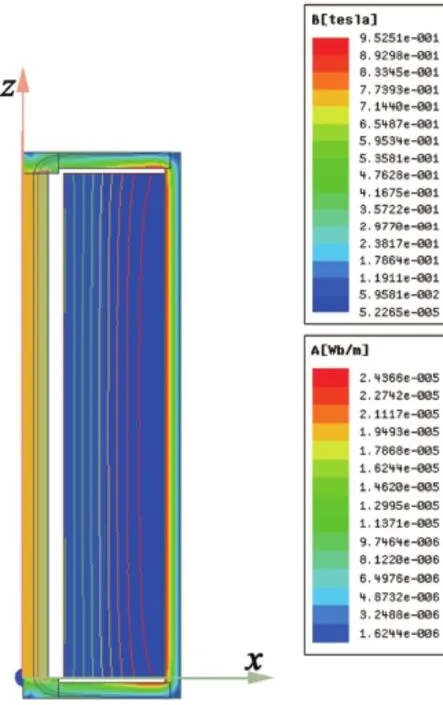
图4 a1=8 mm,δ=25 mm时内径磁力线和磁通密度分布

图5 形状因数Gcoil随a1,δ变化云图
随着a1和δ的增大而增大,并且存在最优点,但要达到这个最优点,致动器的外径会非常大,考虑实验环境接口以及致动器重量的限制,将线圈外径限定在50 mm以内,即在本致动器的设计中线圈外半径不可超过25 mm,即有如下关系式:

该限定区域在图5中为直线以下部分,提取原始数据得到a1和δ满足要求的最优取值组合:

磁场的均匀性可以通过增加补偿线圈或者改变轭铁的形状来实现。本文从后者入手,保持磁路封闭情况下,线圈越长,顶头越长,以线圈比材料棒多出的长度h为变量,单独进行参数化模拟并得到沿轴线场强分布如图6所示。可见,随着线圈超出棒材部分长度的增大,沿轴线场强的均匀度逐步恶化,不均匀度从3%发展到90%,磁场的过度不均匀会导致材料的性能变差,降低棒材的输出力和位移,因此采用h=0时的方案,即线圈长度等于棒材长度100 mm。

图6 不同线圈长度下沿轴场强分布
3 实验研究
3.1 超磁致致动器实验研究
根据前文所述的致动器参数如表2所示。实验测试平台如图7所示,考虑棒材需要在合适的压应力偏置下工作,通过预紧螺钉以及植入称重传感器来监视棒材受力情况;变频电压源可以提供不同幅值的AC+DC电压;激光位移传感器来测量输出顶头的位移值;整个致动器外围包裹水冷,将其温度控制在25℃±2℃之内。
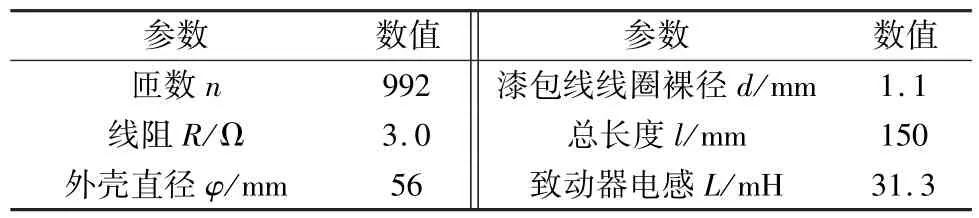
表2 致动器参数

图7 位移测试系统
在不同预紧力情况下对致动器输入不同直流电得到相应的变形值结果如图8所示。磁致应变ΔS随着电流的增加而增加,磁致伸缩系数d经历了由大变小的过程,在电流低于4 A时应变跟电流呈较强的线性关系,并且应变系数很大,随后趋于平缓;电流为8.5 A时达到最大应变1 100 ppm,此时偏置压力为400~700 N,对应压应力为5~9 MPa。

图8 不同偏置压力下静态磁致应变
固定预紧力5 MPa,线圈通4 A的偏置直流电,在此基础上叠加50 Hz不同幅值的交流电压,得到一系列不同的位移振幅,其峰-峰值Ap-p随电压变化如图9所示。随着叠加的交流电压幅值的增大,输出位移近似线性增长,当电压超过20 V,输出位移增长幅度减小;超过25 V后交流电幅值超过直流偏置,导致输出波形波峰变平现象,这是因为超磁致材料在H=0附近应变值非常小,反映在输出波形上即随着电流的变化,位移基本不变的情况。
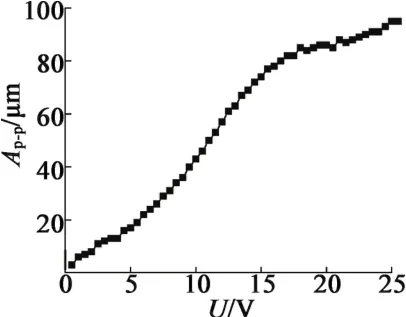
图9 4 A直流偏置时位移-电压曲线
保持直流偏置电压不变,交流电压固定为25 V,频率从10 Hz变化至150 Hz得到致动器的位移-频率响应曲线,如图10所示。致动器可以看成是电阻电感串联,随着频率升高,其总阻抗Z~=R+jωL的幅值|Z~|会增加,导致内部电流峰-峰值减小,另一方面,超磁致材料本身具有的“磁滞”现象也会随着频率的增高而逐渐使输出位移变小。
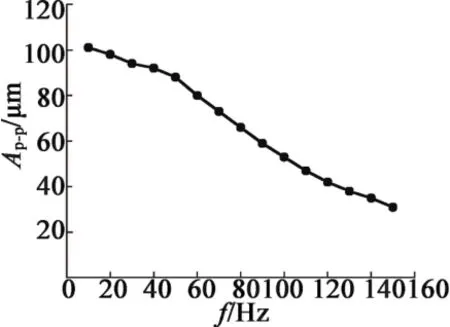
图10 振幅峰-峰值随频率变化曲线
3.2 隔膜泵的实验研究
将金属隔膜泵体接到致动器的后端,通过导杆将振动传递到隔膜上,配合单向阀片来实现流体工质的单向输运并对泵进行性能测试。实验测试平台如图11所示,整个实验在大气环境中进行,管路中植入压力传感器和体积流量传感器,通过阀门手动调节泵的背压。

图11 隔膜泵性能测试平台示意图
测试得到一系列的压头与流量的输出关系曲线,如图12所示,流动工质为乙醇。在11.8 V(DC)和25 V(AC),50Hz的电压驱动下,金属隔膜泵具有最大流量2 mL/s,最大压头接近202.650 kPa。在此基础上固定电压幅值,改变输入频率得到泵的流量-频率曲线,如图13所示。其中流量的理论值计算如下:

图12 压头-体积流量曲线
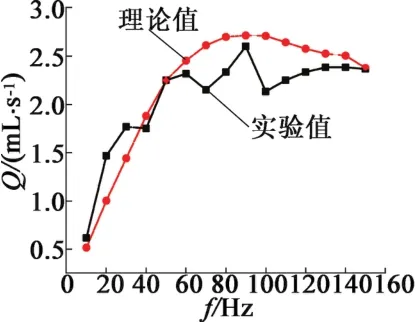
图13 不同频率下的理论-实验流量对比
实际隔膜泵工作频率为10~100 Hz,远小于金属隔膜的共振基频(模态分析结果为2 950 Hz),因此可以认为致动器对隔膜的驱动为准静态驱动,隔膜并未发生共振,单冲程的流量即为隔膜变形的扫

式中:f为驱动频率;Am为隔膜面积,直径为34 mm的圆;Ad为导杆与隔膜接触面积,直径12 mm;Ap-p为该频率下致动器的最大位移输出,具体数值如图9所示。
由图13可见,流量的实验值与计算值在实际运行频率范围内基本吻合,均是在频率较低时线性上升,到一定程度后基本保持不变。过圆台体积,因此理论流量估算:
4 结 语
本文介绍了用于驱动金属隔膜泵的超磁致伸缩致动器的磁路设计以及实验验证,主要包括以下内容:
基于有限元软件MAXWELL对致动器磁路进行了仿真,通过真实结构的形状因数来衡量磁路结构的合理性,从而得到了最优的线圈内外径参数以及合适的长度;
对致动器的静态与动态位移输出进行了测试,结果为最大磁致应变达到1 100 ppm,最大振动输出值为 100 μm;
搭载隔膜泵进行了性能测试,50 Hz下该泵具有最大2 mL/s的流量输出,频率变化下的流量输出与计算值符合得一致。
参考文献
[1] 王博文.超磁致伸缩材料制备与器件设计[M].北京:冶金工业出版社,2003.
[2] 王传礼,丁凡,张凯军.超磁致伸缩执行器及其在微小流体泵中的应用[J].液压与气动,2002(11):26-28.
[3] ANJANAPPA M,BI J.A theoretical and experimental study of magnetostrictive mini-actuators.Smart Materials and Structures[J].1994,3(2):83-91.
[4] LASER D,SANTIAGO J.A review of micropumps.Journal of micromechanics and microengineering[J].2004,14(6):37-64.
[5] RICHTER M,LINNEMANN R,WOIAS P.Robust design of gas and liquid micropumps[J].Sensors and Actuators A Physical,1998,68(1-3):480-486.
[6] LIU D H,LIU L W,TANG G,et al.A design and research on GMM precision flow pump[J].Applied Mechanics&Materials,2014(8):117-121.
[7] ENGDHL G.Handbook of giant magnetostrictive materials[M].LosAngele:Academic Press,2000,.
