Δ-ΣADC在旋变解码与电流采样中的应用

钟再敏,陈振挺

(同济大学,上海201804)

0 引 言

从20世纪80年代开始,Δ-Σ型模数转换器(以下简称ADC)在通讯领域以及高保真音响中已经得到了广泛应用,它已成为高精度ADC设计的一种切实可行的解决方案。如今,这类ADC也被应用在了动力电子和电驱动控制系统中。

Δ-ΣADC的基本原理是过采样和频谱整形。如图1所示,整个Δ-ΣADC由抗混叠滤波器、调制器和降采样数字滤波器组成[1]。调制器是数模转换器的关键,它以远超过信号奈奎斯特频率的速率实现量化功能,同时通过误差反馈进行频谱整形,将量化噪声从低频推向高频。高阶调制器一般采用MASH(multi-stage noise shaping)结构,其中每一级的结构都是稳定的1阶或2阶结构[2]。

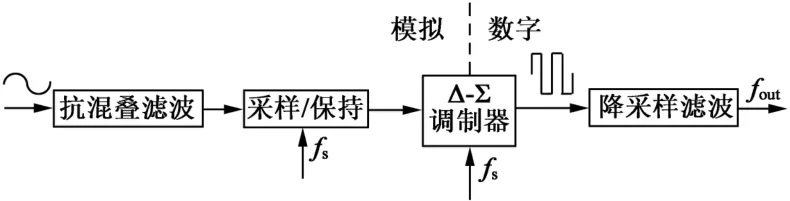
图1 Δ-ΣADC结构示意图

降采样数字滤波器的作用是把频带外的噪声滤除。降采样数字滤波器需要具有平坦的信号通带、陡峭的转换带以及足够衰减能力的截止带,一般分为两级[3]。第一级大多采用结构简单的级联型梳状滤波器(以下简称CIC),将采样频率降至奈奎斯特频率的2～4倍。第二级采用有限冲击响应滤波器(以下简称FIR),将输出频率降到奈奎斯特频率。

旋转变压器(以下简称旋变)作为车用永磁同步电机主要使用的角度传感器,目前大多数解调方案仍采用轴角变换芯片[4]。本文的旋变软件解码方式,能够省去昂贵的解码芯片,具有较高的解码精度,在汽车行业具有较好的应用前景。同时,将ΔΣADC应用在电机电流/位置同步采样之中,也具有较高的可行性。

1 Δ-ΣADC在旋变解码中的应用

旋变是一种电磁式传感器,用来测量旋转物体的转轴角位移和角速度。对于可变磁阻式旋变而言,初级绕组和次级绕组均位于定子上,两个定子绕组机械错位90°,转子的特殊设计使得次级耦合出的电压随着角位置变化而发生正弦变化。激励信号与返回正余弦信号如图2所示[5-6]。旋变输出电压(S3-S1,S2-S4)的计算公式如下:US3-S1=E0sin(ωt)·sinθ US2-S4=E0sin(ωt)·cosθ式中:θ为轴角,ω为激励角频率,E0为激励幅度。

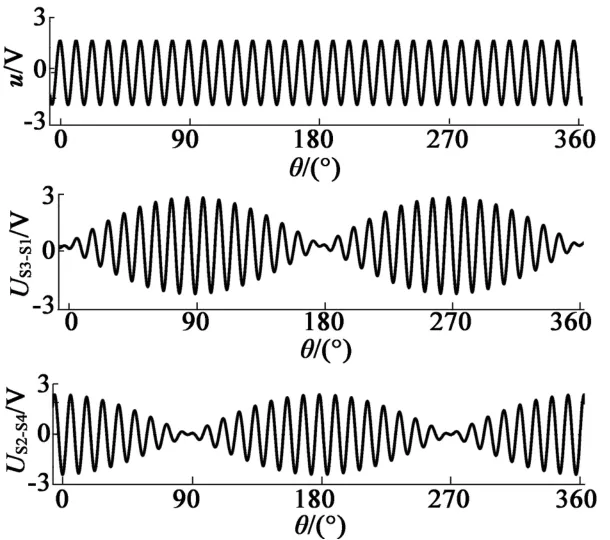
图2 旋变激励信号与正余弦返回信号

1.1 DSADC模块配置

英飞凌新一代Tricore架构的TC275芯片是一款专用于车用电机控制的微处理器,芯片的SPB总线上带有一个DSADC(Δ-ΣADC)模块。这个模块含有六路并行的Δ-ΣADC通道,通道上都有专门用于旋变解码的整流器和积分器环节。它在旋变解码中的应用如图3所示。完成旋变解码需要芯片外硬件电路、两路DSADC模块硬件电路配置以及软件算法的相互配合,所以将这种解码方式可称之为旋变软件解码。

激励信号由DSADC模块内部的载波生成器生成,整流器与其互通,获取信号翻转时刻。从芯片中发出的数字PWM波,经过激励电路形成比较完美的激励正弦波。而返回缓冲电路将差分正/余弦信号的电压调整到芯片允许的范围内。

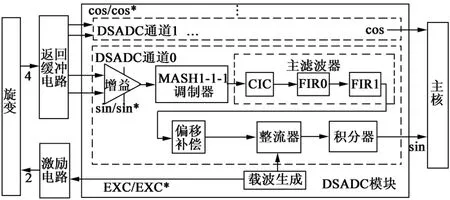
图3 DSADC模块在旋变解码中的应用

以差分正弦信号为例,进入DSADC模块后首先经过一个运算放大器,将差分信号做差,并放大两倍。然后,MASH1-1-1调制器将其调制为数字信号,后通过滤波器链滤波。滤波器链中的CIC的降采样率为16,级联阶数为3;两级FIR滤波器的参数固定和降采样率为2。整流器根据激励信号的相位对返回信号进行翻转,便于信号进行积分[7]。

积分后的正/余弦值就是软件算法的输入,该值并不在[-1,1]范围内,而是倍乘了一个系数,该系数与激励信号幅值、旋变变比、运放增益、滤波器阶数等都有直接关联。

1.2 旋变软件解码仿真

我们在Simulink中完成了旋变软件解码的信号离线仿真,仿真采用定步长,步长为1.25×10-8s(即频率为80 MHz),求解器为ode4,总体仿真结构图如图4所示。

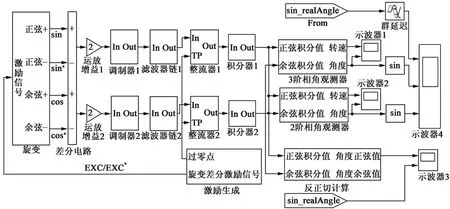
图4 旋变软件解码Simulink仿真

Simulink仿真中各模块的构造与配置与现实情况基本一致,软件算法尝试了反正切函数与相角观测器。

如图5所示,仿真中分别对CIC,FIR0和FIR1的幅频特性进行了分析。CIC和FIR0提供了衰减能力较好的截止带,而 FIR1能提供平坦的通带和陡峭的转换带。

图6(a)、图6(b)分别展示了整流器和积分器的特性。其中,整流器能够按照规定的相位对信号进行翻转;积分器能提取输入信号包络线,角度正余弦量的最终输出频率为9.765 625 kHz(周期为102.4 μs)。

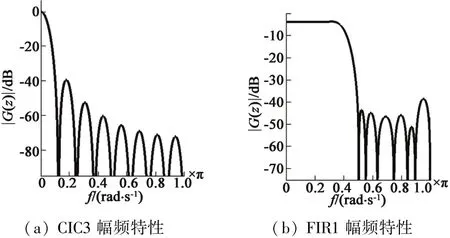
图5 主滤波器链滤波特性

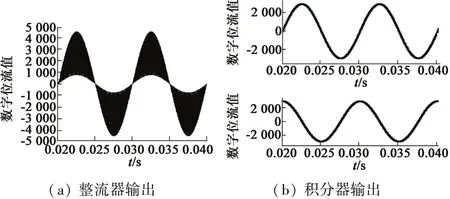
图6 整流器和积分器的输出

1.3 相角观测器

利用反正切函数可以简单获取旋变角度,但是这种方法有抗噪性差、静态波动大、无法产生转速值等缺点。

如图7所示,反正切函数获取的角度值与较真实角度有相位延迟。

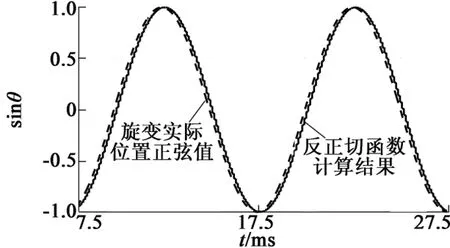
图7 用反正切函数获得角度值后取其正弦量

相位延迟分为两类,第一类别是滤波器群延迟(Group Delay)造成的相位滞后,这种延迟是FIR型滤波器造成的,时间延迟固定,在滤波器设计阶段就能确定。第二类是微处理器外围设备寄存器等待主核读取所花费的时间,它在仿真中并不体现,通常通过时间差(Time Stamp)的方式来补偿。延迟的总相位可以按以下公式来补偿:

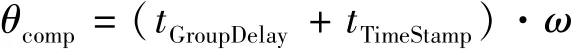
旋变软件解码中每个环节造成的群延迟如表1所示。

表1 降采样滤波器中各模块的群延迟时间

相角观测器实际就是将数字锁相环的原理运用在角度观测中。一个二阶相角观测器如图8所示,各滤波器造成的群延迟在这里进行补偿。

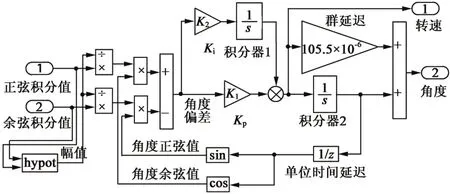
图8 二阶相角观测器原理图

2 Δ-ΣADC在电流/位置同步采样中的应用

电流采样与旋变解码在电机磁场定向控制(以下简称FOC)中十分重要,并且二者是相互关联的,必须保持电流值与旋变角度值是在同一时刻产生的,才能进行坐标变换。传统ADC电流采样与旋变硬件解码是通过同步PWM触发的机制来保障同步采样的。而基于Δ-ΣADC的电流/位置同步采样意味着,在电机控制中电流采样与旋变位置解码都采用Δ-ΣADC原理。采用这种模式有以下几个特点:

1)电流采样电路不需要抗混叠滤波器;

2)电流采样精度可以达到13 bit或更高;

3)电流采样和旋变软件解码有各自的群延迟,若二者接近,可缩小延迟补偿范围。

2.1 DSADC模块配置与电流采样仿真

调制器的工作频率升至20 MHz,CIC降采样率升至64,整流与积分环节被旁路,其余与旋变解码的配置相似。另外,当时间差生成之后会申请中断,开始执行FOC程序。

最终电流采样的输出频率是78.125 Hz(周期为12.8 μs),而总群延迟为 107.55 μs。 而旋变软件解码的总群延迟为105.5μs,二者非常接近。也就是说,抛开时间差的问题,两者的理论采样时间几乎一致,将相角观测器补偿的群延迟从105.5μs降到了-2.05 μs。

仿真中Δ-Σ调制器的负端接地,调制器和降采样滤波器按照设计参数进行搭建。如图9所示,延迟了107.55μs的正弦信号幅值为200 A,频率为300 Hz,它与Δ-ΣADC的采样结果几乎重合。

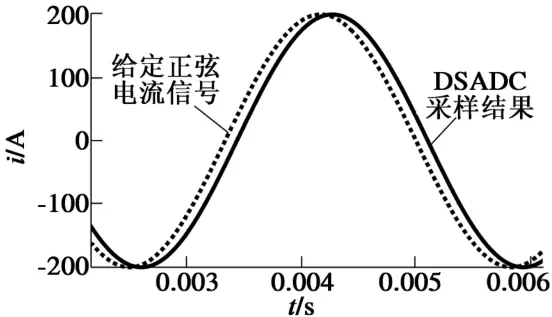
图9 基于Δ-ΣADC电流采样仿真结果

2.2 同步方案

同步方案的信号关系如图10所示,旋变软件解码的输出周期为102.4μs,电流采样的输出周期为12.8μs,FOC的触发周期为100μs。信号 Dsadc-Trigger的上升沿同时锁存电流采样和旋变解码的结果值,但是需要将旋变角度值同步到实际电流采样点上。

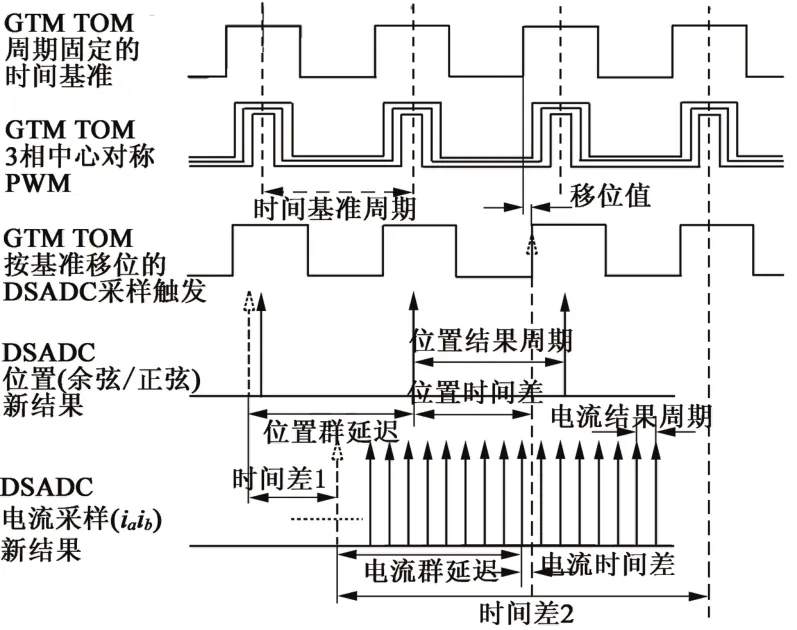
图10 Δ-ΣADC电流/位置同步采样信号图

图10 中的空心箭头表征了实际电流采样点和旋变位置采样点,时间差1为补偿时间,其公式:

T1=GDPos-GDi+TSPos-TSi(4)

式中:T1为补偿时间;GD代表群延迟,TS代表时间差。图10中的变量代表的具体时间长度如表2所示。

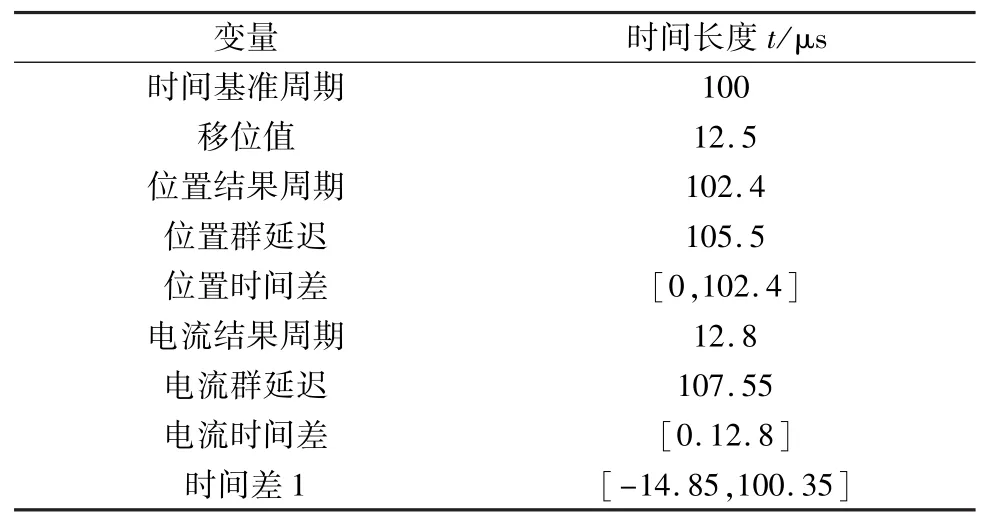
表2 图10中各变量的意义

经计算,在这种模式下旋变软解码需要补偿的时间延迟为[-14.85μs,100.35μs]。而在 Δ-Σ ADC仅用作旋变软件解码的情况下,补偿时间为[105.5 μs,207.9 μs]。

从结果显而易见,软件解码相角观测器补偿的最大延迟时间下降了107.55μs,即电流采样的群延迟。

3 实验结果与分析

在完成仿真验证及电机控制板制作后,对电机控制板做了硬件在环(以下简称HiL)测试。

如图11所示,在HiL平台上模拟了永磁同步电机、旋变、光电编码器和逆变器等部件。其中电机参数以一款真实电机为样本,电机极对数与旋变极对数均为3。

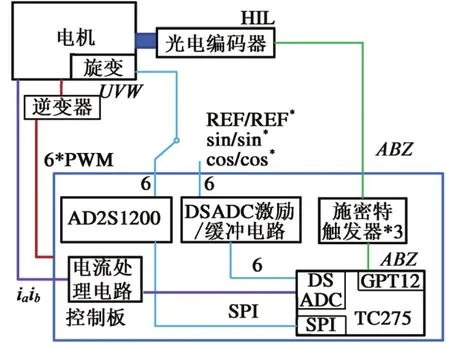
图11 HiL测试平台架构框图

在控制板处,我们有3种不同的方式来获取旋变位置,分别是采用解码芯片AD2S1200的硬件解码、采用光电编码器的增量式编码和采用Δ-ΣADC原理的旋变软件解码,其中最后一种是待验证的算法。这里增加一路光电编码器是因为HiL平台无法同时给出两路旋变信号。

3.1 旋变软件解码HiL测试结果

验证的思路是首先对比硬件解码和增量式编码,保证后者的正确性,没有固定时间的延迟。经验证,这两种算法在不同转速下都能获得一致的旋变位置,电角度偏差在全转速范围内偏差为±0.26°电角度。

然后再对比增量式编码和旋变软件解码,由于无法用较高的速率观察DSADC模块内部信号,只能通过CAN观测积分器输出的最终结果。如图12所示,正余弦量的正余弦度较好。

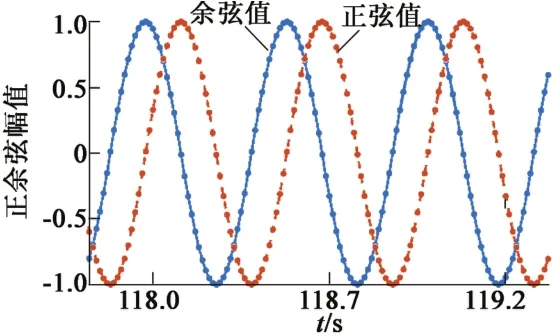
图12 DSADC模块输出的正余弦值(50 r/min)

旋变软件解码验证结果如图13所示。通过HiL测试可以发现,无论硬件解码、增量式编码和旋变软件解码都能较好地获取旋变位置及电机转速。若以增量式编码为基准,旋变软件解码能够用算法修正的方式克服相位延迟的问题,并在全转速范围内能够将最大偏差限制在±0.7°(电角度)内,且急加速急减速的情况依然能够较好适应。

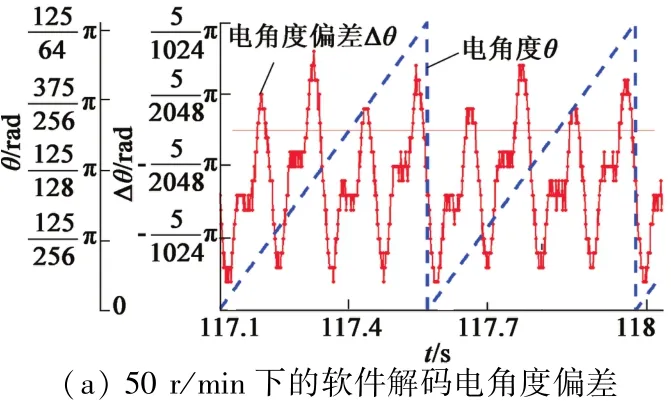
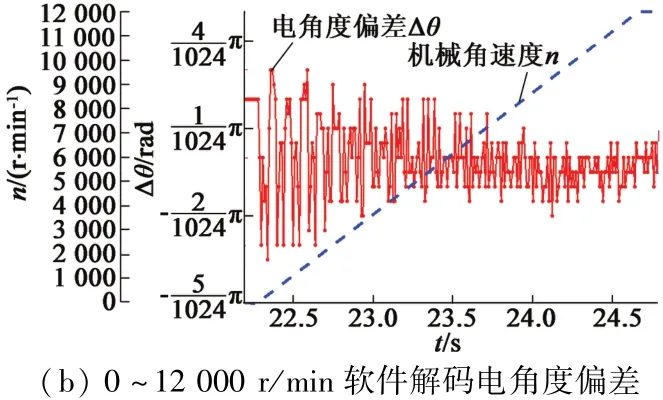
图13 光电编码器与旋变软件解码的电角度偏差

3.2 电流/位置同步采样HiL测试结果

在HiL平台中设定一个稳定的d,q轴电流(id=-100 A,iq=200 A)以及一个稳定的转速(5 000 r/min),通过Δ-ΣADC电流/位置同步采样计算得到的d,q轴电流如图14(a)所示。可以看到,Δ-Σ ADC具有采集三相电流的能力,在不同转速的情况下,计算得到的d,q轴电流在给定的范围附近。

如图14(b)所示,将电机控制在5 000 r/min,80 N(id=-235 A,iq=305 A)的工况下。三相电流幅值和相位稳定,反馈回来的d,q轴电流波动较小。

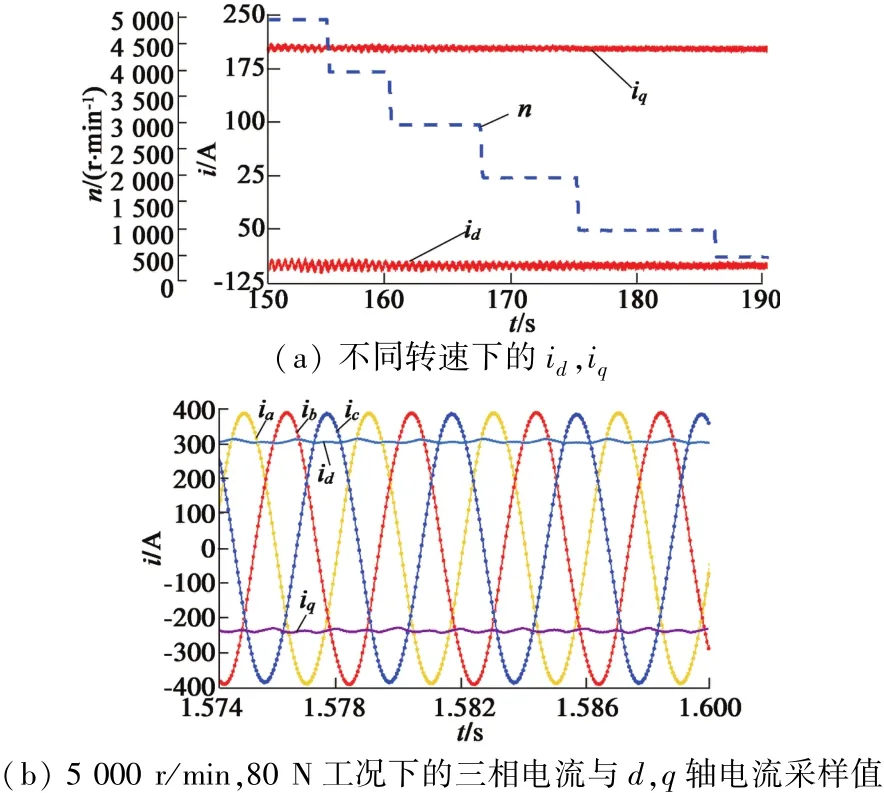
图14 电流/位置同步采样测试结果

HiL测试的结果表明,基于Δ-ΣADC的电流同步采样是一种切实可行的方案,该方案的关键在于做好电流与旋变位置的同步采样。虽然该方案本身不能使电流采样和旋变位置采样在同一时刻发生,但是通过机理分析,运用补偿的机制能将电流与旋变位置在坐标变换前做到数值上的同步。

4 结 语

本文将Δ-ΣADC运用于电机旋变解码与电流同步采样中。经硬件在环测试可以证明,旋变软件解码具有较高的准确性,全转速范围内电角度最大偏差为±0.7°电角度,能够替代解码芯片,节省开发成本。电流/位置采样同步方案使得Δ-ΣADC能够同时运用于旋变解码与电流采样中,该方案具有较高的可行性与较强的应用价值。

[1]PETERSW,SCHULZ B,MATHAPATIS,et al.Regular-sampled currentmeasurement in AC drives usingΔ-Σ modulators[C]//2009 13th European Conference on Power Electronicsand Applications,Barcelona,2009:1-9.

[2]吴笑峰.高精度sigma-delta ADC的研究与设计[D].西安:西安电子科技大学,2009.

[3]周伶俐.Sigma-delta调制器的研究及其在SIMULINK环境下建模[D].武汉:华中科技大学,2007.

[4]李超,杨益群,郝旭耀,等.基于∑-Δ调制原理的高精度旋变旋转变量解码系统[J].自动化仪表,2016,37(3):17-22.

[5]KHABURID A.Software-based resolver-to-digital converter for DSP-based drives using an improved angle-tracking observer[J].IEEE Transactions on Instrumentation and Measurement,2012,61(4):922-929.

[6]周长攀,杨贵杰,苏健勇,等.基于△∑调制原理的全数字轴角变换算法[J].电机与控制学报,2013,17(8):78-84.

[7]刘晓璇.基于Δ-∑ ADC的旋转变压器位置解码算法研究[J].信息通信,2016(1):39-40.