体验·感悟·发现

余兰芝

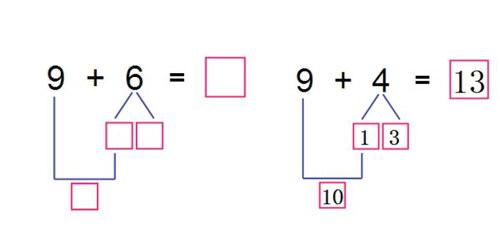
一年级的计算课，尤其需要通过让学生动手操作寻求算理，亲身经历新知识的形成与发展过程。然而，在很多数学课堂中，我们经常会看到“形”和“数”脱节的现象，为了操作而操作，动手操作的实效性没有得到很好的体现。基于此，通过我自己执教的几节一年级的计算课，分别是《5以内的加法》、《9加几》、《十几减9》，谈谈我在一年级计算教学当中是如何将动手操作的有效性落到实处的。

一、在操作中体验算式的意义

《5以内的加法》是学生在小学阶段当中第一次正式接触加法，对于一年级的新生来说，体验算式的意义非常重要。虽然很多学生已经在学前接触过加法，会进行一些简单的加法计算，但是让学生真正地理解加法，并运用加法解决实际问题还是第一次，所以学好这一课对以后的数学学习至关重要。下面两次教学本课时对操作环节进行了不同的处理，教学效果迥然不同。

[第1次教学]

师：3+2为什么等于5？

生：我是数出来的。

生：我是摆圆片的。

师：下面我们用圆片摆一摆。

师引导学生左边摆3个，右边摆2个，摆好后数出是5个。

接下来做“想想做做”第2题，将“画一画“改成“用圆片摆一摆”，再填得数。

[教学反思]

以上教学可以看出学生摆完圆片之后还是依赖“数”得出结果，用圆片代替图，只是从数图到数圆片的转变，学生的思维并没有得到提升。教材当中“想想做做”第2题是要求学生“先画一画，再填得数”，笔者将此处的“画一画”换成用圆片“摆一摆”，“用圆片摆”较“画一画”的优点在于它能做到有效呈现“将两部分合起来”的动态效果，即将原本的结果眭操作换成了过程性操作。然而实际教学当中，由于笔者对为什么这样处理教材并没有真正想清楚，为了操作而摆圆片，错失了这样一个好的素材，只是让学生“摆”出结果而没有让学生经历“合”的过程，学生对于加法含义的理解，即算理却没有得到很好的体现。

[改進后的教学]

师：有的小朋友想到了摆圆片的方法，下面我们就用圆片来摆一摆。

3个0表示什么？2个0呢？将3个0和2个0合起来是几个O？（将两部分圆片合起来）

学生摆圆片表示3+2，得出3+2=5。

师：小猴子知道我们会用摆圆片的方法计算加法，它也想向我们学习呢！（出示“想想做做“第2题）

生先摆圆片，再合起来看看是几，最后填得数。

[教学反思]

第2次教学这部分内容时，操作中增加了将两部分圆片合起来的动态过程，使摆学具的意义得以充分展现：先在左边摆3个圆片，右边摆2个圆片；再把左右两部分合起来，边合边说：3个和2个合起来是5个。如此做法，就让学生在借助学具操作理解算法的过程当中，进一步巩固理解了加法的含义。

二、在操作中感悟算理

数学计算不仅要让学生知道是什么，还要让学生明白为什么，也就是要让学生明白算理。算理就是计算过程中的道理，是指计算过程中的思维方式，解决为什么这样算的问题。那么在计算教学中，如何通过有效的操作让学生感悟算理呢？《9加几》是学生第一次学习进位加法，在这之前，学生已经掌握了10以内的加、减法，并且具备了“几和几凑成十”的有关凑十的经验，有一定的知识基础。本节课旨在让学生通过动手操作，自主探索9加幾的计算方法，并在不同算法的交流中，重点让学生理解“凑十法”的计算思路。教师在某个操作细节上的不同处理，就有可能会影响到整节课的教学效果。

[第1次教学]

出示情境图，得出算式：9+4。

师：9加4等于多少？下面请小朋友们先自己用学具摆一摆，再和同桌说一说你是怎样想的。

（生动手操作，师巡视）

师：谁来说说你是怎样算出来得数的？

生1：我是数着算的，9，10，11，12，13。

生2：从外面散着的拿1个放到盒子里，一盒有10个，外面有3个，一共有13个。

生3：我是先想10加4得14，再减去1就是13。

师：小朋友们用不同的方法都算出了9加4得13。刚才有小朋友说：从外面散着的拿1个放到盒子里，盒子里有10个，再加上外面的3个，得13。哪个小朋友能到前面来演示一下？

（指名上台演示，师逐步对应板书）

师：先算什么？再算什么？

生：先算9加1得10，再算10加3得13。

[教学反思]

课后安排了形如下面的练习：

此练习的目的是突出“凑十”的方法，使学生对“把9凑成10”有个清晰的印象，进一步理解“凑十法”的计算思路，然而有部分学生将第二个加数6分成了2和4，为什么会出现这种现象呢？粗看以上教学环节，步骤清晰，学生操作正确，师生互动配合默契，然而细究下来，教师却忽视了一个很重要的细节：即操作与说理没有进行有效的结合。此处操作关注了算式的结果，而对于算理，即“为什么这样操作”没有使学生明晰，从而使操作流于形式。

[改进后的教学]

师：哪个小朋友能到前面来演示一下？

（指名上台演示，师逐步对应板书）

师：为什么要从4里面拿出1个放到盒子里？

生：这样就可以放满1盒，1盒正好是10个。

引导学生说出：看到9想到1，4可以分成1和3，9和1凑成10，10+3=13。

[教学反思]

改进后的教学，让学生对照实物图交流算法，教师通过问题“为什么要从4里面拿出1个放到盒子里”，有意识地引导学生在移的过程中发现：因为盒子里有9个，9和1凑成10，所以要从外面的4个里拿出1个放到盒子里，使盒子里凑满10个，这里只能将4分成1和3，而不能分成2和2。接下来再引导学生边操作边说出：看到9想到1，4可以分成1和3，9和1凑成10，10+3=13。学生在有效的操作过程中伴随语言的描述明白了算理，使知识与相应的智力活动上升为抽象的内化过程，犹如在算理与算法之间架设了一座桥梁，借助于描述操作过程的语言向概括结论的语言转化，上升为理陛的思考。

三、在操作中发现算法

有了算理的支撑，就为学生理解算法提供了前提。算法就是计算的方法，主要是指计算的法则，解决如何算得方便、准确的问题。算法是对算理的总结与提炼，为计算提供了快捷的操作方法，提高了计算的速度。下面是我执教《十几减9》的一个教学片段。

师：一共有13个桃子，卖了9个，还剩多少个？

生：13-9=4。

师：13-9是不是等于4呢？你能用摆小棒的方法进行验证吗？

（生动手操作，师巡视）

生展示：将13根小棒（1捆和3根）其中的1捆拆开，然后从右往左依次数出9根拿掉，最后数数还剩下4根。

师：这位同学是先拿掉右边的3根，再拿掉左边的6根，还剩4根。（师边介绍“平十法”边板书：13-3-6=4）

师：还有不同的算法吗？

生：因为9+4=13，所以13-9=4。

師：这位同学运用了学过的知识，做减法想加法。（师板书：做减想加）

师：还有不同的算法吗？（课堂一时出现冷场）

[教学反思]

十几减9是退位减法的起始课，“破十法”是一种很重要的方法，虽然教材和教参上首推“想加做减”，因为学生有20以内进位加法的基础，要算13-9，只要想到9+（4）=13，就可以得出答案，但是部分学生本身进位加法计算掌握得还不是很牢，如果依赖于这种方法，适必影响计算的正确和速度。而“破十法”，只要有10以内加减法的基础就能算出来，对于这部分学生来说，只要掌握这种方法，正确率就能明显提高。以上教学片段中，师追问：“还有不同的算法吗？”目的是希望学生还能说出“破十法”。第1位上台展示的学生是这样操作小棒的：先将1捆拆开，然后数出9根拿掉，最后数数还剩4根。教师处理时发现学生是“从右往左”依次数出9根拿掉，于是顺势而导，介绍“平十法”。当然学生的本意并不一定真如教师所介绍的“先拿掉右边的3根，再拿掉左边的6根”，可能只是要“拿掉9根”，教师将学生的拿法有意识地引导到“平十法”。然而教师接下来的提問没有与此处的引导进行有效的对接，教师应通过有效的提问突显不同的拿法，培养学生的方法意识。如可以问一问学生：“要拿掉9根，如果先拿掉右边的3根，还需要从1捆里面拿掉几根？”从而再将1捆拆开，从中拿出6根，使学生意识到刚才的拿法是“先拿掉盒子外面的3个桃，再拿掉盒子里面的6个桃”。再进一步提问：除了这种拿法，还有不同的拿法吗？而不是泛泛地问：“还有不同的算法吗？”问题没有指向于让学生经历不同的拿法得出新的算法，致使学生茫然。

一年级计算课是种子课，应首先让学生体验算式意义，基于算理的感悟，抽象发现出计算方法，形成计算技能，实现计算的自动化，这对于学生未来的学习至关重要。学生在摆学具的过程中，通过教师的有效引导，明白知识的由来，感悟策略的形成，把操作与观察、语言与思维结合起来，上升为理性思考，充分发挥动手操作的实效性。