复杂曲面零件散乱点云特征点提取
2017-05-14李泷杲
高 瑞,李泷杲,黄 翔,李 栋
(1. 南京航空航天大学机电学院,南京 210016;2. 航空工业江西洪都航空工业集团有限责任公司,南昌 330024)
零件的加工及检测是飞机、汽车等机械生产过程中的重要环节。零件的加工质量将直接影响部件及产品的质量与性能。而几何特征是零件几何模型的重要组成部分,对于几何模型的外观描述、模型重建及准确表达具有重要作用[1]。对于一些复杂曲面零件,采用样板、模胎等人工比对的传统检测方式,其评价精度取决于技工经验,无法获得精确的数字量描述,而且效率低。然而,随着三维激光扫描技术的迅速发展,获得高精度、高密度的点云数据已经十分迅捷。因此,通过分析处理零件表面的点云数据,提取出零件的特征,可以实现零件加工质量的定量描述及特征的逆向重构。
点云特征点提取及特征线拟合的研究主要集中两方面,一是基于网格模型的特征提取,二是基于散乱点云的特征提取。
网格模型的特征线提取方法可以分为自动提取与半自动提取。自动提取方法通常是寻找出网格上曲率的突变点作为特征点,然后将这些离散特征拟合成特征线。Yang等[2]通过拟合局部二次曲面计算主曲率与主方向,实现特征线提取,但该方法对噪声点云或稀疏点云不适用。上官宁等[3]通过主成分分析的方法获得主特征方向,沿特征点生长方向寻找后继特征点,实现特征线的提取。刘倩等[4]将点云数据进行高斯映射形成点集聚类,获得曲率和法向量发生突变的点作为特征点。半自动提取是用户交互选取特征线方向的多个点,邻近点相连形成初始特征点,最后采用优化方法优化初始特征线。刘胜兰等[5]采用追踪投影法确定初始特征线,通过Sanke变形满足主动轮廓能量最小实现特征线优化,但是点云模型的网格重建耗时长,网格的成形质量对特征线的提取影响较大。
相比较于网格模型的特征线提取,散乱点云没有任何拓扑信息。目前,直接从散乱点云中提取特征的研究相对较少。Gumhold等[6]提出的方法是根据邻域点的协方差矩阵的特征向量的特征值给每一点一个权重,将点区分为边界点、折点、平面点和角点,利用点邻域边权值生成最小生成树,剪除树枝,最终得到平滑的曲线。Pauly等[7]在Gumhold的基础上,采用了一种多尺度的点云特征提取算法,该算法在不同尺度上提取特征,这种方法更为抗噪稳健。Weber等[8]提出了基于高斯映射的点云聚类的方法提取尖锐特征的方法,在其算法中,首先计算一点及其邻域点所构成的所有三角形,并计算出三角形的法矢,将法矢映射到高斯球上后通过高斯聚类的方法统计判断是否为特征点,为了避免噪声的影响,他们也提出了一种自适应的阈值计算方法;然而,该算法受噪声影响较大,一个点若因为噪声的影响而形成错误的三角形,会导致错误的聚类,从而不能进行正确的判断;同时,计算点云中每个点与其邻域点的三角形,会产生很大的时间开销。庞晓旭等[9]通过拟合局部的最小二乘曲面的多项式来计算每个点的主曲率,将主曲率绝对值较大的点标识为谷脊特征点,将特征点投影到潜在特征线上得到增强特征点,最后经过平滑处理得到谷脊线,该方法计算相对复杂,但对稀疏点云模型具有较好的处理效果。王小超等[10]提出了基于局部重建的点云特征提取算法,首先通过协方差分析获得初始特征点,在初始特征点的基础上在局部区域进行三角形重建,通过法向聚类形成局部数据点的分类,将分类点进行平面拟合,并判断是否落在多个平面上进行特征点的提取。张雨禾等[11]同样采用基于局部重建的提取方法,不同的是最后依据Weingarten映射性质来进行谷脊特征点提取。吾守尔·斯拉木等[12]提出了一种基于平均曲率运动的尖锐特征提取方法,但仍需要人工调节自由参数。
基于上述分析,本文提出了复杂曲面零件散乱点云特征点的提取方法,旨在将零件的几何特征提取出来,一方面可以为后续零件的数字化检测提供依据,另一方面可以作为曲面重建的约束条件。
算法分析及实现
首先,对点云建立基于KD树的拓扑关系,实现快速检索每一点的k近邻点;然后,采用基于高斯权重的主成分分析法完成对点云模型的初始标记;最后,通过基于标记的自动识别法实现特征点的检测,聚类处理完善特征,如图1所示。

图1 方法流程Fig.1 Flow of the proposed method
1 点云拓扑关系的建立
散乱点云分布无任何规律,且没有任何拓扑连接信息,单点无法提供任何有效的特征信息。为了能够从点云中提取特征点,点云中的每一个点必须从它的临近点中收集信息。因此,需要检索点云的k近邻点。k近邻的搜索方法通常有3种:空间栅格法、八叉树法与KD树法。空间栅格法,方法简单但受点云采样密度的影响较大;八叉树法,将空间分为8个卦限,非叶子节点继续分为8个卦限,在叶子节点中存储信息,但占用的空间较大,存在冗余现象,不适合存储数量较多的点云;而KD树法相对简单,它的最差复杂度是o(3N2/3),平均复杂度是o(log/n )[13]。因此,利用KD树可以加快近邻点的搜索,可以改善算法的运行时间,提高效率。本文不详述KD树的建立过程。
2 基于高斯权重的主成分分析法
在传统主成分分析的基础上,本文提出基于高斯权重的主成分分析法。
散 乱 点 集 p={p1,p2,p3,…,pn},pi∈R3,i=1,2,3,…,n,定义 Np为采样点pi∈p的k近邻点集,C为点pi的近邻点的构成的协方差矩阵:

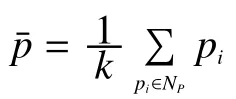

(1)散乱点云中每一点与其近邻点的距离并不相同,显然离中心点较近的点对中心点的影响更大,应占有更大的权重因子,而公式(1)中近邻点对中心点的影响权重是一样的。因此,采用高斯权重可以根据距离中心点的远近赋予不同的权重因子。
(2)点云密度是影响特征点提取的关键因素之一,而高斯权重函数包含了点云密度这一影响参数。
3 点云特征提取
3.1 点云初始标记


图2 不同区域位置的点的特征指标Fig.2 Feature index of points in different regions
由图2可以看出:位于平面处的红色点来说,随着k值的变化,特征指标变化不大,全部近似为零;位于棱边处的蓝色点,其特征指标比较大,且随着k值的增加相对稳定,特征指标全部大于0.1;而对于靠近特征点的一些点(图2中绿色点)来说,由于当近邻点增加时可能会包含棱边处的特征点,所以随着k值的增加,特征指标存在突变。因此,对于邻近棱边处的点pi来说,当与的差值较大时,将终止迭代,并将ωkpi作为点pi的最佳特征指标,在算法中将作为迭代终止条件。为避免陷入无限循环,需要限制迭代的次数,如果迭代10次仍然没有满足终止条件,算法就自动停止迭代,并以最后一次的特征指标作为最佳指标。
虽然ωp反映了一个点是否为特征点的可能性,但在试验中发现很难确定一个合适的阈值来得到完整的特征点集。本文通过选取两个较为宽松的阈值,对点云进行初始的标记,尽可能地保留潜在特征点,在后续的特征点完善中精确提取。假设两个阈值 ω_< ω+,对于任一点 pi的特征指标 ωpi,如果 ωpi≤ ω_,则认为该点不是特征点并标记为0;如果ωpi≥ω_,则认为该点是特征点并标记为 2;如果 ω_< ωpi< ω+,则认为该点为潜在特征点并标记为1,最后进一步识别与完善。

3.2 特征点识别与完善
点云数据在全局阈值ω_与ω+的条件判断下,初始区分为特征点集、非特征点集与潜在特征点集。潜在的特征点采用基于标记的自动识别法实现特征点的提取。对于潜在特征点集中的任一点Pi来说,依次考虑以下4种情况。
(1)若该点的近邻点的标记全部为2,即全为特征点,则认为该点是特征点,将标记置为2。
(2)若该点的近邻点的标记全部为0,即全为非特征点,则认为该点是非特征点,将标记置为0。
(3)若该点的近邻点的标记为0或1,即潜在特征点与非特征点,则进行以下判断:
如果 ωpi≥ max{ωp1,ωp2…ωpk},即该点的特征权重是其所有近邻点的特征权重的最大值,则认为该点是特征点,将标记置为2。
(4)若该点的近邻点的标记中既有特征点(标记为2)且至少含有两个特征点,又有其他类型的点(非特征点或者潜在特征点)。为了判别该点是否是特征点,本文提出一种基于欧式距离的识别方法,具体步骤如下:
步骤1,计算潜在点p近邻点中任意两个特征点之间的欧式距离,。
步骤2,计算潜在点p与近邻特征点之间的欧式距离,且Tm=2。
步骤 3,如果 min{dpm}<min{dij},则认为潜在点p为特征点,将标记置为2。
对潜在特征点集中的每一个点进行上述处理后,获得初步的特征点集。然而,当点云模型表面的曲率较大时,因受曲率的影响,曲面上的一些点的特征权重较大而被误判为特征点,如图3所示,因此需要将这些点去除掉来完善特征的提取。试验发现,这些异常点在提取的特征模型中相对比较孤立,且特征点之间的距离一般小于初始点云的平均点间距;基于上述特点进行聚类处理,其步骤如下:
步骤1,将特征点集F中的所有点初始标记为未分类,记作flag=False;
步骤2,取特征点集中的任意一点fi,且flag(fi)=False。在特征点集中寻找fi的最近邻点fi.min,计算di=║fifi.min║。若,则将两点fi, fi.min归为一类Ci;否则,划分为两个类。上述分类后,flag=True。
步骤3,再从特征点集中再取一未被标记的点fj,flag(fj)=false。在特征点集中寻找fj的最近邻点fj.min,计算 dj=║fj-fj.min║,有以下 3 种情况 :
(1)若,且 fi.min∈ C'(C'为已存在的类),则点fj划归到类C'中。
(2)若,且flag(fi.min)=False,则将两点fj, fj.min划归为一类Cj。
(3)若,则将两点fj, fj.min分为两个类。
上述分类后,flag=True。
步骤4,重复步骤3,直到特征点集中的每一点的flag全部为True。
通过上述的聚类处理,特征点集已经被划分为几个类,若类中点的数量小于10个点,则删除这个类及类中的点,剩余的点集即为最终的提取结果。图3显示了聚类处理过程。

图3 特征点聚类处理Fig.3 Feature points clustering
试验结果与讨论
先对本文方法的参数选择进行说明,然后在不同的点云模型进行试验验证。与传统的PCA方法、Web[8]方法进行比较,本文方法更加简单有效。试验在Visual Studio 2010编程环境下进行,硬件环境为奔腾处理器,双核,工作频率为3.06GHZ,内存为4G,PC机。
1 参数选择策略
通过上述分析,本文中的参数主要是两个初始阈值ω_,ω+及初始的近邻点数k;对于初始的近邻点数一般取8~15个点,如果近邻点数取得过小,拟合后几乎全是微小平面,求得特征指标近似为零,不能有效地提取特征点;当近邻点数取得过大时,由高斯函数的意义可知,对于离中心点很远的点来说,高斯权重几乎为零,对结果不会产生太大的影响,却增加了算法的计算代价。因此,本文主要讨论初始阈值对提取效果的影响及其选择策略。
对于阈值下限ω_,主要是保证去除平面点,可以将数值选取的稍微小一些,这样既可以保证去除的点完全属于平面点,又不会去除潜在的特征点,通过试验发现ω_在0.005~0.010之间取值时较为适宜;对于阈值上限ω+,则取值应该稍微大一些,保证特征指标大于该值的点全部为特征点。试验中ω+分别取0.01、0.05、0.10、0.15、0.20、0.25、0.30,ω_取 0.005,并统计各自提取的特征点的数量,如表1所示,特征点的提取效果如图4所示。分析特征点的提取结果可知,当特征指标取得较小时,如ω+ = 0.01,ω+ = 0.05,提取的特征点数量比较多,保留了大部分的特征点,却也包含了许多非特征点,容易使特征变模糊;当特征指标取较大值时,如0.10、0.15等,特征点数量减少的同时较好地保留了点云模型特征,便于后续的点云处理;当进一步增大初始阈值,由图5可以看出特征点的数量几乎不再变化。因此,可以根据实际情况进行初始阈值的选择,当提取的特征要求不是特别精细时,可以适当减小初始阈值。本文建议初始阈值上限在0.10~0.30之间进行选择。

图4 不同阈值下的特征点提取效果Fig.4 Feature point extraction under different thresholds

表1 不同阈值下特征点数量统计
2 试验结果分析
以扇盘(Fandisk)模型为例,该模型不仅有比较显著的曲线、直线特征,还包含相对弱的特征(扇形区域的曲线特征),因此对该模型的提取结果能够有效反映算法的处理效果。在参数选择上,本文选取ω_= 0.003,ω+ = 0.10,初始的近邻点k = 8;PCA方法分别设置阈值ωp= 0.01、0.05、0.10。试验结果如图6所示。当阈值取得较小时,如图6(d)所示,虽然点云的处理结果保留了大部分的特征点,但可以看到特征点附近的很多点被误判为特征点,致使特征变得模糊;当阈值较大时,如图6(e)、6(f)所示,虽然特征更加清晰,在一定程度上缓解了阈值较小时所带来的问题,但有一部分特征点没有识别出来,致使特征不够完整。采用本文的方法,如图6(b)所示,处理结果一次提取就较为完整地识别出了全部的特征点,而且有效地去除了一些对特征点识别贡献不大的点,使提取的特征更加清晰;同时该方法在处理过程中不需要过多人为修改参数。本文也与Web方法[8]进行了比较,采用Web方法中的局部自适应阈值识别法,设置初始阈值参数,近邻点数k = 8,敏感性参数σ = 0.1,提取结果如图6(c)所示,由于Web方法在构造初始三角形集合时存在三角形大量跨越特征区域的问题,故而会导致弱特征丢失的现象。
本文方法又在复杂曲面零件锥形齿轮与整体叶盘的点云模型上进行了试验验证,特征点提取结果良好。
图7(a)是锥形齿轮的原始点云模型,模型共有46300个点。图7(b)显示了本文方法提取的特征点,共有2606个点。轴心的圆形特征点提取效果明显,轮齿处的特征点略显粗糙,但基本完整。
图8(a)是整体叶盘的原始点云模型,模型共有290762个点。图8(b)显示了利用本文方法提取的特征点,共有6932个点,可以看到叶片曲面处的复杂曲线特征点得到了完整的提取。图8(c)显示了特征点集与CAD数模的粗配准,特征点的提取位置基本准确。

图5 不同阈值下特征点数量变化Fig.5 Variation of feature point number under different thresholds

图6 Fandisk点云模型特征点提取Fig.6 Feature point extraction of Flandisk model

图7 锥形齿轮点云模型特征点提取Fig.7 Feature point extraction of bevel gear model

图8 整体叶盘点云模型特征点提取Fig.8 Feature point extraction ofblisk model
结论
本文提出了一种复杂曲面零件散乱点云特征点提取的方法。首先,通过本文提出的基于高斯权重的主成分分析法估计局部曲面的变化程度,对点云模型进行特征点的初始标记;然后,基于标记的自动识别法进行特征点的检测提取;最后,通过特征点聚类处理的方式完善了提取的特征点。试验结果表明,本文方法直接操作于散乱点云,无需进行点云的三角网格重建,处理过程简单有效且无需过多的参数调整,特征点提取较为完整,对于复杂曲面零件的数字化检测及逆向重建具有重要意义。然而,必须指出的是,当点云模型的采样质量较差,点云分布十分不均,采样点过于稀疏时,本文方法的处理结果并不理想,因此这将是下一步的研究重点。同时,基于特征点实现特征曲线的拟合也是希望实现的目标。
参考文献
[1]胡事民,杨永亮,来煜坤.数字几何处理研究进展[J].计算机学报,2009, 32(8):1-18.
HU Shimin, YANG Yongliang, LAI Yukun. Research progress of digital geometry processing[J]. Chinese Journal of Computers,2009,32(8):l-18.
[2]YANG M, LEE E. Segmentation of measured point data using a parametric quadric surface approximation[J]. Computer-Aided Design, 1999, 31(7):449-457.
[3]上官宁, 刘斌. 三角网格模型特征线提取方法[J]. 华侨大学学报(自然科学版),2010, 31(5):487-490.
SHANGGUAN Ning, LIU Bin. Investigation of feature line extration triangular mesh model[J].Journal of Huaqiao University(Natural Science),2010, 31(5):487-490.
[4] 刘倩, 耿国华, 周明全, 等. 基于三维点云模型的特征线提取算法[J]. 计算机应用研究 , 2013, 30(3):933-937.
LIU Qian, GENG Guohua, ZHOU Mingquan,et al. Algorithm for feature line extration based 3D point cloud models[J]. Application Research of Computers, 2013, 30(3):933-937.
[5]刘胜兰, 周儒荣, 张丽艳. 用主动轮廓模型优化网格曲面上的特征线[J]. 计算机辅助设计与图形学学报, 2004,16(4):439-443.
LIU Shenglan, ZHOU Rurong, ZHANG Liyan. Feature line optimization on triangular sufaces using active contour model[J]. Journal of Computer-Aided Design and Computer Graphics,2004, 16(4):439-443.
[6]GUMHOLD S, WANG X, MACLEOD R. Feature extraction from point clouds[C]//Proceedings of the 10th Internation Meshing Roundtable, Newport Beach, 2001.
[7]PAULY M, KEISER R, GROSS M. Multiscale feature extraction on point-sampled surfaces[J].Computer Graphics Forum, 2003, 22(3):281-289.
[8]WEBER C, HAHMANN S, HAGEN H. Sharp feature detection in point clouds[C]//Shape Modeling International Conference, IEEE Computer Society, 2010:175-186.
[9]庞旭芳, 庞明勇, 肖春霞. 点云模型谷脊特征的提取与增强算法[J]. 自动化学报,2010, 36(8):1073-1083.
PANG Xufang, PANG Mingyong, XIAO Chunxia. An algorithm for extraction and enhancing valley-ridge feature from point sets[J].Acta Automatica Sinica, 2010, 36(8):1073-1083.
[10]王小超, 刘秀平, 李宝军,等. 基于局部重建的点云特征点提取[J]. 计算机辅助设计与图形学学报, 2013, 25(5):659-665.
WANG Xiaochao, LIU Xiuping, LI Baojun,et al. Feature detection on point cloud via local reconstruction [J]. Journal of Computer-Aided Design and Computer Graphics, 2013, 25(5):659-665.
[11]张雨禾, 耿国华, 魏潇然. 散乱点云谷脊特征提取[J]. 光学精密工程, 2015,23(1):310-318.
ZHANG Yuhe, GENG Guohua, WEI Xiaoran. Valley-ridge feature extraction from point clouds[J]. Optics and Precision Enginering,2015, 23(1):310-318.
[12]吾守尔·斯拉木, 曹巨明. 一种新的散乱点云尖锐特征提取方法[J]. 西安交通大学学报 , 2012, 46(12):1-5.
WUSHOUR Slam, CAO Juming. An extraction algorithm for sharp feature from point clouds[J]. Journal of Xi’an Jiaotong University,2012, 46(12):1-5.
[13]LEE D T, WONG C K. Worst-case analysis for region and partial region searches in multidimensional binary search trees and balanced quad trees[J]. Acta Informatica, 1977, 9(1):23-29.
[14]PAULY M, GROSS M, KOBBELT L P. Efficient simplification of point-sampled surfaces[C]// Visualization conference,IEEE(2002), Boston, 2002.
