小学渗透数学思想方法的途径

贺李

摘 要：小学数学课堂教学中，教师可以在复习导入、新知探究、巩固练习和总结反思等各个环节充分地渗透各种常见的数学思想方法，促进学生对数学知识的深刻理解，从而使学生的数学思维能力得到提高。

关键词：小学；教学；数学思想方法

中图分类号：G62 文献标识码：A 文章编号：1673-9132（2017）13-0074-02

DOI：10.16657/j.cnki.issn1673-9132.2017.13.041

数学思想是指数量关系和空间形式反映在人的意识中经过思维活动而产生的结果，是对数学知识和方法的本质认识，是对数学规律的理性认识。数学方法是指在解决数学问题和数学地解决问题的过程中所采用的途径、程序和手段。从概念上来看，这两者既有联系也有区别，但是从数学教学实践的角度来看，我们没有必要去做过于严格的区分。所以，当无法确定是数学思想还是数学方法时，我们可以统称为数学思想方法。

在小学阶段，常见的数学思想方法有画图、列表、假设、比较、分类、化归、集合、数形结合等等。数学思想方法在小学数学教学中的渗透，不仅有助于教师深入挖掘教材，增进自身的教学水平，还有助于学生数学素养的提高。那么，在小学渗透数学思想方法都有哪些途径呢？下面我将结合实际谈谈自己的看法。

一、在复习导入时渗透

随着新课改的深入，越来越多的教师在课前导入环节都较多地使用有趣的情境导入，复习导入似乎显得有点落伍了。其实不然，情境导入固然有自身的优势，然而复习导入也并非一无是处。通过课前复习，一方面可以唤起学生对旧知识的回忆，从而有利于新知识的嫁接；另一方面也能够通过归纳总结直接得出新的更加深刻的知识，比如思想方法层面的知识。因此，作为小学数学教师，我们可以在课前引导学生复习的过程中经常性地渗透数学思想方法。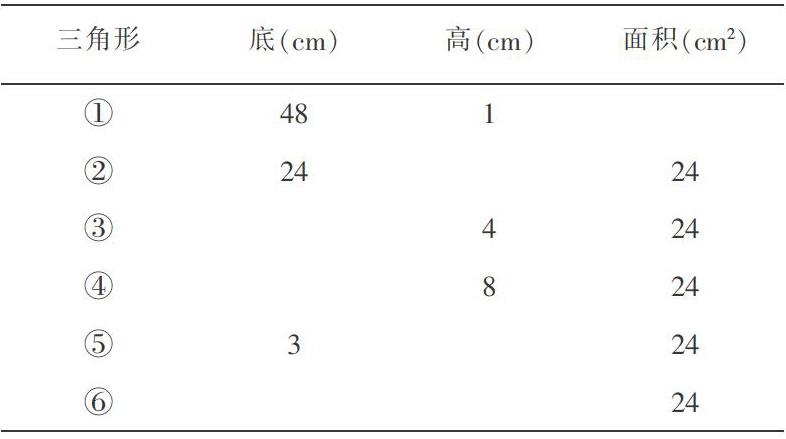

比如，在教学人教版小学五年级上册“梯形的面积”这节课时，教师就可以通过复习导入引出化归这一重要的数学思想方法。因为在此之前，学生已经学习了平行四边形和三角形的面积公式的推导方法。其中，平行四边形的面积公式是先把平行四边形转化为长方形后推出来的，三角形的面积公式则是先把三角形转化为平行四边形推出来的。在这两种图形的面积公式的推导过程中，都用到了化归的思想方法，在这里都是转化为求一个已学图形的面积。具体来说，教师可以先引导学生回忆平行四边形和三角形的面积公式的推导过程，然后引导他们通过比较得出共同点，最后教师再顺势引出化归法，并让学生猜一猜梯形的面积可以转化为哪种图形的面积。

二、在新知探究时渗透

数学上的发现大都和数学思想方法密不可分，在看似冰冷的数学概念和规则的背后实际上都隐藏着数学家火热的思考。因此，在数学新知识的学习过程中，教师可以通过设计适当的问题情景，让学生在独立思考与合作探究活动中去感悟数学思想方法，体验数学思想方法在问题解决和知识生成中的意义和价值。尽管课堂上的数学探究不同于数学科学研究，但在这个过程中，同样需要学生的思维和情感的参与，同样需要数学思想方法的运用。

例如，在教学人教版小学五年级上册“小数乘小数”时，教师可以灵活运用教材，结合学生的生活现实创设出他们感兴趣的问题情景，然后让他们根据已知条件和问题列式计算。在实际的教学中，教师可以通过这样的设计给学生充分的时间去思考，去交流，必要的时候给予提示和启发。在实际教学中可以发现，大部分学生都能独立或在他人的帮助下，结合之前学过的知识算出正确的结果。他们会联系小数点位置移动引起小数大小变化的规律，将小数乘法转变成整数乘法，然后根据整数乘法的计算方法得出结果，最后算出了原来小数乘法的积。不可否认，通过探究法来学习新知不如讲授法那般省时省力，然而直接演示并告知学生计算方法不能强烈地激发起他们思维的火花，更不能让他们深刻地感受到化归这种思想方法所起到的奇妙的作用。

通过新知探究渗透数学思想方法并非只有高年级才可以进行，在低年级同样可以将数学思想方法的种子播撒到学生的心里，让其生根发芽。实际上，在教学10以内的数的认识时，教师就可以让学生初步感悟归纳概括的数学思想方法。教师可以通过很多具体的事物使学生体会这些数的意义，并在这个基础上归纳概括出10以内的数。

三、在巩固练习时渗透

新知探究诚然是渗透数学思想方法的绝佳途径，不少的教师都很珍视这一良机。然而，有的教师就到此为止了，他们在巩固练习中大都设计的是“双基”的演练，很少有数学思想方法的用武之地。这样，就不可避免地导致了新知探究中的渗透只是蜻蜓点水式的 “渗”，学生浅尝辄止式的“悟”。所以，教师还应当把巩固练习这个课堂上的半壁江山作为渗透数学思想方法的重要阵地。在巩固练习时，教师可以设计一些分层练习，既有基本知识和技能的强化训练，也有一些需要运用数学思想方法才能有效解决的问题，这样就能多给学生一点感悟数学思想方法的机会。

例如，教師可以在人教版小学五年级上册《三角形的面积》的练习中提出这样的问题让学生思考和解决：

1.在表格里填上合适的数。仿照例子在方格图中画出三角形。

2.请结合表格和图，找出当三角形面积不变时，它的底和高的变化规律。

在做这道练习题的过程中，学生不仅需要灵活运用三角形的面积计算公式来解决问题，还直观地感受到了当面积不变时底和高的变化规律，体验到了数形结合这一重要的数学思想方法的作用。

四、在总结反思时渗透

目前，很多教师在一堂课快结束时都会问学生的收获，意在让学生回顾一下本节课的学习内容，当学生实在说不上来之时，教师就代为总结，时间控制在一两分钟左右。诸如此类的做法不能说没有必要，然而缺少了学生对数学学习过程的反思。我认为，在小学数学课堂教学中，教师应该引导学生总结，更应该引导学生反思。通过对新知探究过程和解决问题过程的反思，可以让学生回顾用到的基本知识和技能，同时也能让蕴含在其中的数学思想方法渗透得更加明晰。

例如，在教学人教版小学四年级下册《三角形的分类》时，当学生按照角的特点把不同的三角形分成直角三角形、锐角三角形和钝角三角形之后，教师可以引导他们反思，让他们说一说这样分的原因。这样，学生在交流中就可以更加清晰地体会到分类的原则，即标准要统一并且不重不漏，对分类这一重要的数学思想方法就会有更加深刻的理解。最后，教师还可以引导学生用集合图来表示直角三角形、锐角三角形和钝角三角形之间的关系，以此来渗透集合的思想方法。

总而言之，小学数学教师应该注重在课堂教学的各个环节有意识地不失时机地渗透数学思想方法，让数学思想方法遍地开花，随时可见，随处可用，进而提高他们的数学思维水平和数学素养。

参考文献：

[1] 赵德生，赵静.小学渗透数学思想方法的实践与思考[J]. 教育， 2015（39）：183.

[2] 徐中春.浅谈小学数学课堂教学中渗透数学思想方法的途径[J]. 教育教学论坛， 2009（8）：66-67.

[ 责任编辑 杜建立 ]