基于蛛网结构和双曲线的定位算法

2017-05-13欧阳林群阮承治

长江大学学报(自科版) 2017年5期

关键词：蛛网同心圆阅读器

欧阳林群,阮承治

(武夷学院机电工程学院，福建武夷山 354300)

基于蛛网结构和双曲线的定位算法

欧阳林群,阮承治

(武夷学院机电工程学院，福建武夷山 354300)

为提高蛛网定位算法的精度，提出了一种基于蛛网结构和双曲线的定位算法。首先按照蛛网拓扑结构放置射频参考标签，在蛛网中心安装阅读器；然后对蛛网结构的主弦和辅弦节点分别构造同心圆，找出距离待测标签最近的同心圆；接着采用最近同心圆上参考标签坐标和待测标签坐标的双曲线关系，利用最大似然估计法求出待测标签坐标；最后对提出算法的精度进行计算，与当前流行的蛛网定位算法进行对比试验，验证了该算法的有效性。

射频识别；蛛网拓扑结构；双曲线；定位算法

随着物联网技术的不断发展，目标定位技术越来越受到人们的关注，定位精度的要求也越来越高。射频识别(Radio Frequency Identification,RFID)是物联网领域的核心技术，是一种利用射频方式进行非接触双向通信的自动识别技术。RFID基本系统包括阅读器和电子标签，阅读器和标签通过阅读器天线和标签天线的耦合完成信号的传输[1]。相比于红外、蓝牙、超声波、Global Position System(GPS)等技术，射频识别技术具有非视距、非接触、定位精度高、成本低等优点，成为室内定位的首选[2]。随着室内定位技术的发展，出现了大量的定位算法，主要分为到达时间法(Time of Arrival，TOA)、到达角度法(Angle of Arrival，AOA)、接收信号强度法(Received Signal Strength Indicator，RSSI)和到达时间差法(Time Difference of Arrival，TDOA)4类。对于室内多径效应产生的信号干扰，接收信号强度法表现出优于其他3种方法的抗干扰性能，因此更适合于室内环境的定位[3]。

目前典型的RFID定位系统主要有Spoton系统，Virtual Reference Elimination (VIRE)和LocAtioN iDentification based on dynaMic Active Rfid Calibration (LANDMARC)系统等。在LANDMARC系统中，选取最接近待测标签信号强度的参考标签，运用权重质心法计算待测标签坐标[4]。在LANDMARC 系统的基础上，李纲等提出了蛛网定位算法用于改进定位精度，该方法采用最接近待测标签信号强度的相似环中参考标签坐标估算待测标签坐标[5]。为进一步提高蛛网算法的定位精度和实现更小距离的精确定位，笔者提出了一种基于蛛网结构和双曲线的定位算法。

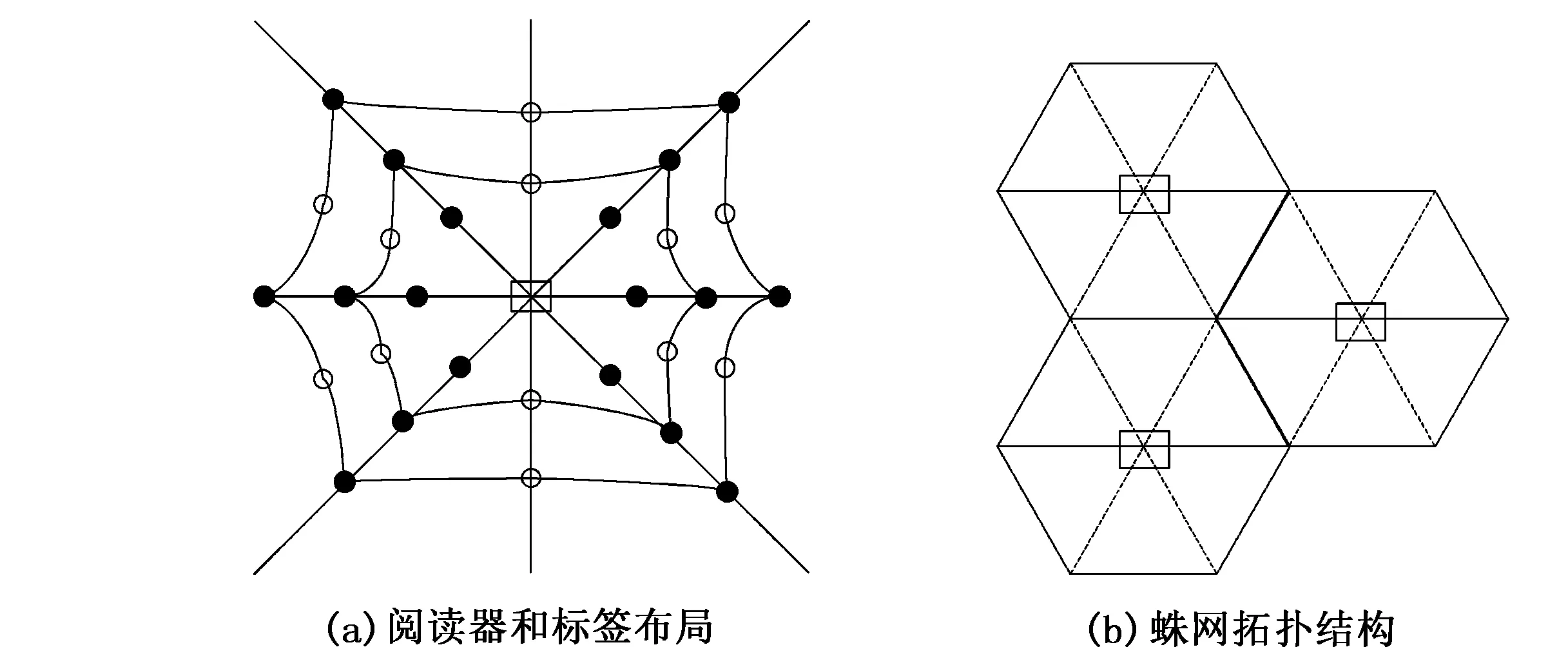
图1 蛛网结构图

1 基于RFID的蛛网结构

通过RFID定位系统发现，为精简标签和阅读器数目以实现系统的高效定位，定位参考标签往往按照一定的拓扑结构分布[6]。受蜘蛛结网猎取食物的启发，将射频阅读器作为蛛网的中心，在蛛网的节点处安装射频参考标签，如图1(a)所示。黑色实心点为蛛网主弦上均匀分布的节点，空心点为蛛网辅弦上均匀分布的节点，该结构能够有效减少参考标签的数量且实现定位。将图1(a)的蛛网拓扑结构分布到整个待定位区域，能够实现定位区域间的无缝连接和定位系统的实时定位[7]，如图1(b)所示。

2 定位算法

2.1 最近同心圆的选取

图2 阅读器和标签位置示意图

图2为蛛网结构中的阅读器和标签位置示意图，实心点和空心点代表蛛网结构中的参考标签，五角星代表待测标签，方框代表阅读器。其中，每6个一组实心点和每6个一组空心点构成不同半径的同心圆。

为了初步确定待测标签的位置，需要找出与待测标签距离最近的同心圆。将阅读器接收到的参考标签的信号强度设置为矩阵A：

(1)

将阅读器接收到的待测标签的信号强度设置为矩阵B：

B=[B1，B2，…，BL]

(2)

其中，Aij(i=1,2,…,m;j=1,2,…,n)表示第i个同心圆的第j个参考标签的信号强度；Bk(k=1,2,…,L)表示第k个待测标签的信号强度。

将式(1)中的矩阵A每一项减去Bk，得到的矩阵Mk中均值最小的一行对应的参考标签组成第k个待测标签的最近同心圆。矩阵Mk为：

(3)

通过式(3)可求解并找出与待测标签最近的同心圆。

2.2 待测标签的定位

图3 双曲线定位原理图

基于第k个待测标签与其最近同心圆中的6个节点的位置关系，采用双曲线定位求出待测标签的坐标。双曲线定位原理如图3所示，其基本原理如下：实心五角星为待测标签，T1、T2和T3分别为第k个待测标签与其最近同心圆中的6个节点中的3个；待测标签与参考节点标签(T1、T2和T3)之间的距离分别为d1、d2和d3；待测标签与参考标签T1和T2的距离差为d21,则被测标签一定处于以T1和T2为焦点，焦距为d21的双曲线上；同样地，待测标签与参考标签T1和T3的距离差为d31,则被测标签一定处于以T1和T3为焦点，焦距为d31的双曲线上；2组双曲线的交点S就是待测标签的坐标(如图3中的五角星)。

假设待测标签的坐标为(x,y)，T1、T2和T3的坐标分别为(x1,y1)，(x2,y2)， (x3,y3)，则有：

(4)

该方程属于高次方程，理论上存在s和s′这2个解，可通过Matlab中的指令求解方程。然而，现实情况下该方程只有1个解。通过参考信息和一定经验可以消除掉运动位置不确定点，笔者采用式(3)去验证所求待定位标签坐标点是否满足最近同心圆条件，达到去除点s′的目的。

若使用多参考标签进行定位，则待测标签的求解就转化成一个概率分布问题，采用极大似然估计算法确定待测标签的最可能坐标[8]。已知m个参考标签的坐标是(xi,yi)(i=2,3,…,n;j=1,2,…,m,i>j)，其与待定位标签的距离为dij可表示为：

(5)

为求出待定位标签坐标(x,y)，将式(5)写成AX=B的形式[9]。已知dm(m-1)为dm和d(m-1)的矢量差，则式(5)可以转化为：

(6)

将式(6)转化为通式形式：

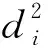
(7)

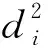
(8)

将式(6)转化成矩阵AX=b的形式，则：

X=(ATA)-1ATb

其中：

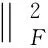
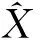
3 试验结果与分析

为了对笔者提出算法的精度进行验证，将笔者提出的基于蛛网结构和双曲线的定位算法(记为H-CLA)与蛛网定位算法(记为CLA)[5]进行比较。文献[5]中将待测标签分为3类，如图4所示。3类待测标签分别可表示为：

1) 只有1个参考标签靠近待测标签S1，令待测标签坐标等于该参考标签坐标，即(x,y)=(x1,y1)；

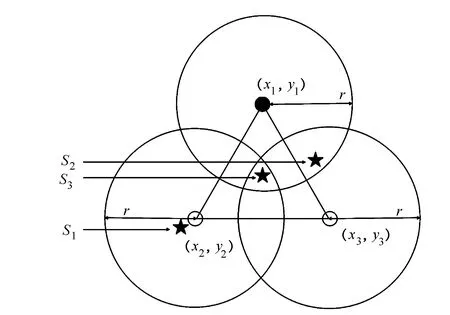
图4 CLA算法标签分布图

2) 只有2个参考标签靠近待测标签S2，待测标签坐标等于这2个参考标签坐标的中点，即(x,y)=；

3)待测标签S3位于3个参考标签中间，采用LANDMARK算法求出待测标签坐标，如式(9)：

(9)

笔者采用如图2所示的蛛网结构在拓扑结构中分布24个参考标签和1个阅读器，放入10个待测标签进行仿真。设定参考标签的距离为1.85m，参考标签的扫描半径为1.2m。图5为H-CLA算法和CLA算法的定位坐标与待测标签真实坐标的对比图，红色圈表示待测标签真实坐标，绿色星号表示CLA算法的定位坐标。蓝色五角星表示H-CLA算法的定位坐标。由图5可见，蓝色五角星比绿色星号更接近红色圈，表明采用笔者提出算法得出的待测标签的坐标更加接近真实坐标，其误差更小。

采用H-CLA和CLA算法分别对待测标签的坐标进行定位仿真，采用定位误差累计分布函数(Cumulative Distribution Function, CDF)评价H-CLA算法和CLA算法[10]。仿真100次，2种算法的CDF曲线如图6所示。CLA算法的最小误差为0.284m，最大误差为0.783m，50%的误差小于0.575m；H-CLA算法的最小误差为0.157m，最大误差为0.368m，50%的误差小于0.229m。从结果来看，H-CLA算法定位存在明显的优势。

图5 H-CLA和CLA算法的定位坐标与真实坐标对比图图6 H-CLA和CLA算法的CDF对比曲线

为研究参考标签距离与定位精度之间的关系，由误差公式：

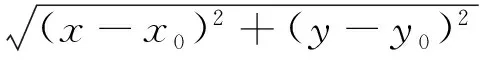
(10)

可得出待测标签的误差平均值：

(11)

仿真得到H-CLA和CLA算法的参考标签距离与平均误差之间的关系曲线如图7所示，采用CLA算法平均误差较小且平滑的区间落在1.2～3.3m，而H-CLA算法的平均误差较小且平滑的区间落在0.2～4.8m。结果表明，H-CLA算法比CLA算法更能应用于精度要求较高的近距离定位，在较大的参考标签距离内保持定位误差平均值较小且稳定，能有效减少蛛网节点的标签个数，优化蛛网拓扑结构和减少系统成本。