基于蚁群优化的选择性集成数据流分类方法

王军，刘三民，刘涛

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)

基于蚁群优化的选择性集成数据流分类方法

王军，刘三民，刘涛

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)

基于集成学习的数据流分类问题已成为当前研究热点之一，而集成学习存在集成规模大、训练时间长、时空复杂度高等不足，为此提出了一种基于蚁群优化的选择性集成数据流分类方法，用蚁群优化算法挑选出优秀的基分类器来构建集成分类模型。该方法首先对所有基分类器采用交叉验证计算分类精度，同时采用Gower相似系数求出基分类器之间的差异性，然后把分类精度和分类器差异性作为分类器挑选标准，从全部基分类器中选出一部分来构建集成模型，最终挑选的基分类器不仅具有良好的分类精度，同时保持一定差异性。在标准仿真数据集上对构建的集成分类模型进行仿真试验，结果表明,该方法与传统集成方法相比在准确率和稳定性方面均有显著提高。

数据流分类；概念漂移；选择性集成；蚁群优化算法；差异性

随着信息化技术的发展和应用需求不断深入，数据流已广泛存在于各行各业，如网络数据、天气预测数据、无线传感数据、金融和电网数据等[1]。如何挖掘出这些数据流中有价值的信息，已成为当前研究的热点问题。而数据流隐含噪声同时具有时序特性和概念漂移现象，导致传统分类模型难以适应数据流的分类问题。

目前，国内外关于数据流分类已取得较多研究成果，以集成学习作为数据流分类模型已成为主流。把集成学习引入到数据流分类中，不仅提高了算法学习精度，增强了学习能力，同时还强化了算法在复杂环境中的学习效果。Street等[2]较早将集成学习应用到数据流分类中，保持集成规模不变，用新分类器替换旧分类器实现对新知识的学习。而概念漂移发生初期体现新概念的基分类器不足以抗衡其他分类器，导致该算法在概念漂移发生初期对样本无法准确分类，鉴于此,Wang等[3]在SEA算法基础上提出改进算法AWE，该算法根据基分类器对最新训练样本的分类准确率来设置分类器权值，给准确率高的基分类器分配较高权重，有效增强集成模型预测精度。针对数据流出现概念漂移导致分类模型频繁变更问题，Farid等[4]基于集成学习实现了一种自适应数据流分类方法，使集成分类模型保持良好的稳定性和灵活性。随后，毛沙沙等[5]利用旋转森林策略获得样本子集来训练分类器，使基分类器之间保持一定差异性，提高集成模型泛化能力。同年，Liao等[6]针对数据流分类问题提出一种新的集成分类模型，通过灵活分配基分类器权重使集成分类模型快速适应数据流中概念漂移的发生。与此同时，Gogte等[7]结合聚类思想实现一种混合集成分类模型，能快速捕获概念漂移，同时有效解决已标记样本少难题；邹权等[8]基于集成学习并结合分层思想在层级结构基础上通过集成学习来构建分类模型，使集成学习更加灵活的应用于数据流分类；针对含噪动态数据流分类,王中心等[9]实现了一种自适应集成分类算法，采用Bayes过滤噪声，通过动态更新分类模型来快速适应概念漂移。从以上研究可以看出，采用集成学习进行数据流分类具有明显优势。而从现有文献分析可知，通常采取增加基分类器数量来提高集成模型的分类精度和泛化能力，使集成规模不断增大，不仅导致存储空间急剧增加，同时集成规模过大导致集成模型训练时间长、算法时空复杂度高等问题。为此，笔者提出了一种基于蚁群优化的选择性集成数据流分类方法。

1 蚁群优化算法

蚁群算法最早由意大利学者Dorigo Macro等[10]在人工生命会议上提出，随后国内外研究人员对其不断进行改进，开发出多种不同的蚁群算法版本并成功应用于优化领域。夏小云等[11]对蚁群优化算法理论研究进行了系统概述，论述了算法的寻优原理、收敛性、复杂度、近似性等，同时分析总结了蚁群优化算法在求解和优化各类问题上的性能。

蚁群优化算法是模拟自然界真实蚂蚁觅食行为，蚂蚁在走过的路径上释放一种称为信息素的物质同时能感知信息素，该物质对蚂蚁选择路线起到诱导作用，路径上走过的蚂蚁越多信息素含量越高，蚂蚁选择该路径的概率也就越高，最终收敛于最优路径。

蚁群优化算法的基本原理可以用最短旅行商问题予以说明。假设有n个城市，蚂蚁数量为m，dij表示城市i、j之间的距离，τij(t)代表t时刻城市i、j之间的路径上信息素含量，则在t时刻蚂蚁k由城市i转移到城市j的概率为：

(1)

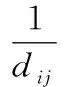
τij(t+1)=(1-ρ)τij(t)+Δτij

(2)

式中,ρ∈(0，1)表示信息素挥发系数； Δτij表示该次迭代中路径ij上信息素的增量，初始时刻为0，计算方法如下：

(3)

(4)

式中，Q为常数表示信息素强度，对算法收敛速度起作用； Lk是第k只蚂蚁在此次循环中走过的路径长度，经过一定次数的循环迭代后，当满足停止条件(收敛或到达循环次数)时，得到最优路径和最短路径长度。

2 选择性集成学习

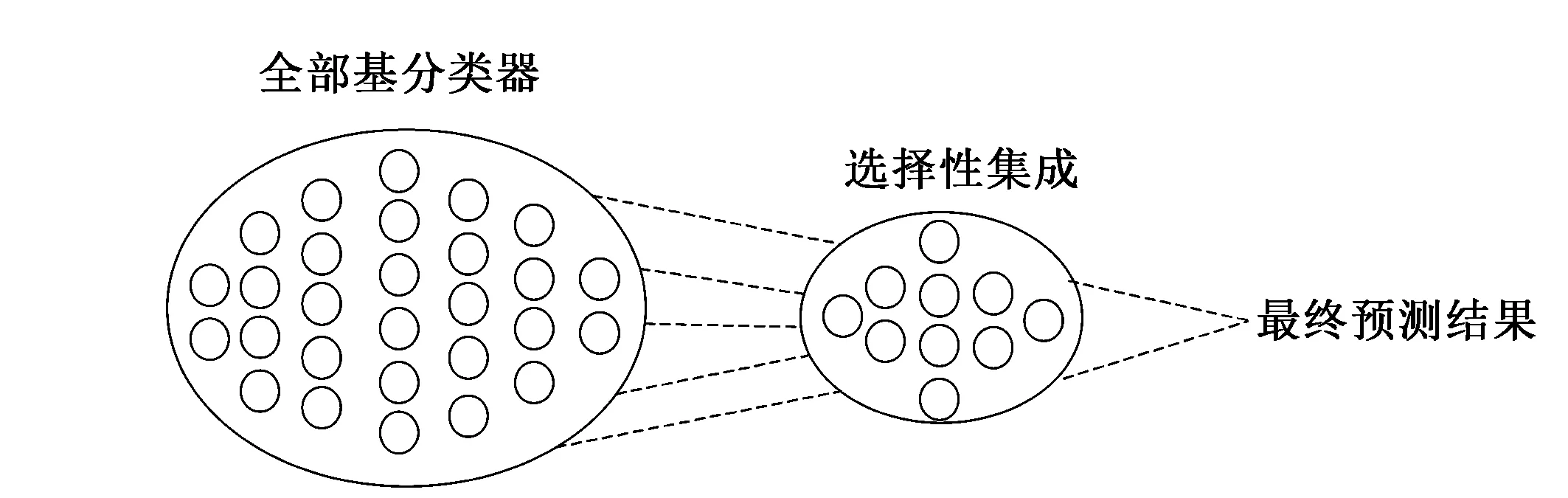
图1 选择性集成原理示意图

选择性集成学习最早由Zhou等[12]提出，其思想是从全部基分类器中剔除作用不大、分类性能不好的分类器，用剩余的分类器构建集成模型能得到更好的预测效果，即“Many Could Be Better Than All”。目前选择性集成已成为集成学习领域预测效果最好的学习范式。其原理示意图如图1所示。

选择性集成作为集成学习中一种新的学习范式提高了集成学习的学习效果，同时解决了集成规模过大带来的困扰。目前选择性集成数据流分类也已取得众多研究成果。赵胜颖等[13]提出一种基于智能群体的选择性神经网络集成方法，利用智能群体的快速收敛提高了算法效率、降低计算复杂度。此外，Liu等[14]基于k-means方法提出一种选择性集成学习算法，克服了集成学习中存储空间大、训练时间长、反复训练等问题。与此同时，为保持集成模型中分类器之间的差异性，该团队又设计一种基于k-均值和负相关的选择性集成学习方法[15]，该方法有效解决基分类器之间的冗余问题，提高了集成模型预测效率。综上可知选择性集成在数据流分类中具有明显优势，而根据挑选规则不同选择性集成可分为基于选择方法、聚类方法、排序方法和优化方法的选择性集成学习算法[16]。其核心思想是根据挑选规则选择部分优秀的基分类器来构建集成模型，从而提高集成模型的分类精度和预测效率同时节省存储空间。其中选择性集成基本框架如下：

1)Input: 训练集T1，验证集T2，基分类器训练算法C，基分类器集合T，选择的基分类器集合S，测评方法M；

2)初始化：基分类器集合T=∅；

3)训练过程：

Fort=1,2,…,T；

得到基分类器集合T={C1,C2,…，CT}；

EndFor

4)选择过程：

在验证集T2上对各基分类器Ct进行测试，得到测试结果Rt,利用测评方法M针对测试结果Rt进行测评；

根据测评结果，挑选出符合条件的基分类器CS添加到集合S中；

5)Output: 选择的基分类器集合S={C1,C2,…，CS}；

3 ACOBSE方法

由于构建分类精度高和泛化能力好的集成分类模型，不仅基分类器要具有较高的分类准确率，同时分类器之间要保持一定差异性。基于蚁群优化的选择性集成数据流分类方法(ACO algorithm Based Selective Ensemble，ACOBSE)就是利用群体智能中经典的蚁群优化算法ACO来选择分类精度高、个体差异性大的基分类器来构建集成模型。该方法首先对训练集采用BatchMode方式训练出多个基分类器，通过交叉验证计算出它们的分类精度，同时采用Gower相似系数计算出基分类器之间的差异性，然后把分类精度和分类器差异性作为基分类器挑选标准从全部分类器中选出部分分类精度高、差异性大的分类器来构建集成模型。该方法不仅减小了集成规模同时利用蚁群优化算法的快速收敛性来提高算法效率。

为便于描述，对常用的基本概念给出定义：

2)概念漂移。是指数据产生的联合概率分布随时间变化而发生不可预知的变化，即Pt(x,y)≠Pt+1(x,y)，其中,x代表样本向量，y表示样本类别。

3)集成学习。对待测样本进行分类时，用若干弱分类器对同一个样本进行预测，再把结果按照某种策略融合获得最终预测结果，集成学习决策函数可形式化为：

其中,ht(x)为弱分类器;HT(x)为集成后的强分类器;at表示基分类器权重。

3.1 交叉验证

交叉验证的基本思想是将数据分为2部分：一部分作为训练集用于分类器的训练，另一部分作为测试集用于分类器预测精度的检验。由于2部分数据不同，使得对预测精度的估计也更接近真实情况。目前常用的交叉验证有K折交叉验证、5×2交叉验证t检验和F检验等。笔者采用的是K折交叉验证t检验方法。

K折交叉验证原理是将数据等分为K份，选择其中K-1份作为训练集用于分类器的训练，剩余一份作为测试集用于分类器预测精度的检验，将K份数据逐一作为测试集进行训练和测试，最终得到K个度量值。K折交叉验证t检验计算方法如下：

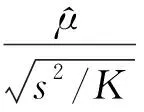
(5)

(6)

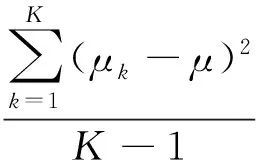
(7)

式中，μk表示在第k折交叉验证算法中度量值的差值。

K折交叉验证t检验主要分为2折交叉验证、5折交叉验证和10折交叉验证t检验，笔者采用K折交叉验证中最常用的10折交叉验证t检验来计算基分类器的分类精度。把分类器预测精度作为挑选基分类器的标准之一，使构建的集成模型获得良好的分类性能。

3.2 分类器差异性

目前对集成学习领域的研究不再局限于对算法的提出和改进，更多关注对基分类器关系的研究，尤其是分类器差异性研究。分类器之间具有差异性是集成分类模型生效的必要条件，同时也是集成模型具有良好泛化能力的关键因素。若集成模型中进行组合的基分类器是相同、无差异的，分类性能并不会提高。因此要提高集成模型的分类性能，基分类器之间必须具有一定差异性，即至少存在一些分类器对其它分类器判断错误的样本作出正确的决策。笔者定义的分类器差异性是结合Gower相似系数计算得到，该计算模型具有分类模型独立和预测能力独立等优点[17]。

为方便描述，假设e表示测试样本，E代表测试样本集，符号de(cx,cy)表示分类器x、y在样本e上的差异性，符号se(cx,cy)代表分类器x、y在样本e上的相似性，二者满足如下性质：

①0≤se(cx,cx),de(cx,cy)≤1；

②de(cx,cy)=1-se(cx,cy)；

结合Gower相似系数计算出分类器基于单个样本的相似性，计算方法见式(8)：

se(cx,cy)=1-δe(cx,cy)

(8)

在式(8)基础上，基分类器基于单样本的差异性计算方法如下：

de(cx,cy)=1-se(cx,cy)=δe(cx,cy)

(9)

(10)

式中, |C|表示样本类别数；概率PDxj(e)表示基分类器x在单个测试样本e上关于类别j的后验概率；PDyi(e)表示基分类器y在单个测试样本e上关于类别j的后验概率；Rj(e)代表测试样本e基于类j的后验概率极差：

Rj(e)=max{PD1j(e),…,PDnj(e)}-min{PD1j(e),…,PDnj(e)}

(11)

综上，在单个测试样本上基分类器差异性计算方法的基础上，可导出在样本集E上基分类器之间的差异性计算方法：

(12)

3.3 ACOBSE算法描述

在上述交叉验证和分类器差异性计算模型基础上，结合多分类器动态集成思想，给出选择性集成数据流分类方法的算法描述。其中DS表示训练数据流，DB代表验证数据集，初始基分类器数量为n，最大集成规模为20，α表示信息素对蚂蚁选择分类器的的作用程度，β表示分类器差异性对蚂蚁选择分类器的作用程度，则ACOBSE算法的详细描述如下：

1)Input: 训练集DS，验证集DB，基分类器数量n，选择的基分类器集合S，集成规模T，参数α，参数β；

2)初始化相关参数：S=∅，T=20；

3)训练过程：

基于训练集DS，采用批处理方式训练出n个基分类器，并用10折交叉验证t检验计算出各分类器的分类精度；

对训练出的基分类器根据式(9)分类器差异性计算方法，基于验证集DB求出基分类器之间的差异性；

4)挑选过程：

蚂蚁首先基于准确率选择一个基分类器并添加到集合S中，同时把该基分类器标记为已访问；

Fort=1,2,…,T；

根据转移概率计算蚂蚁下一个要选择的分类器，转移概率计算方法是基于式(1)思想构建，把分类精度和分类器差异性两者作为相关参数进行基分类器的挑选，具体计算方法如下：

(13)

5)Output：集成分类模型在测试数据集上的分类准确率；

其中，tao(i)表示分类器i的信息素浓度，取值为对应基分类器的分类精度值；differ(j)(i)代表集合S中最新基分类器j与目标分类器i之间的差异性。

4 仿真试验与结果分析

4.1 仿真数据集

试验所用数据集源自平台MOA环境中的移动超平面数据集[18]。该数据集样本属性值在[0,1]，并通过m维度超平面随机生成，样本标签分为正类标签和负类样本2类，在形成数据集过程中主要考虑3个参数n、s、t的变化：噪声参数n表示在数据流中引入的噪声数据量；参数t表示每隔N个样本，样本标签权值的改变量；参数s表示每隔一定数量样本移动超平面方向以概率s发生翻转。规定每个数据集含有2W个样本，并在参数t=0.1、s=10%固定条件下，设置仿真试验数据集共有5个特征属性，其中2个特征属性随时间变化发生概念漂移现象，同时通过改变噪声参数n(0，10%，20%)，即不含噪声、10%噪声、20%噪声，生成3个数据集(记为H0、H1、H2)进行测试。

4.2 试验方案

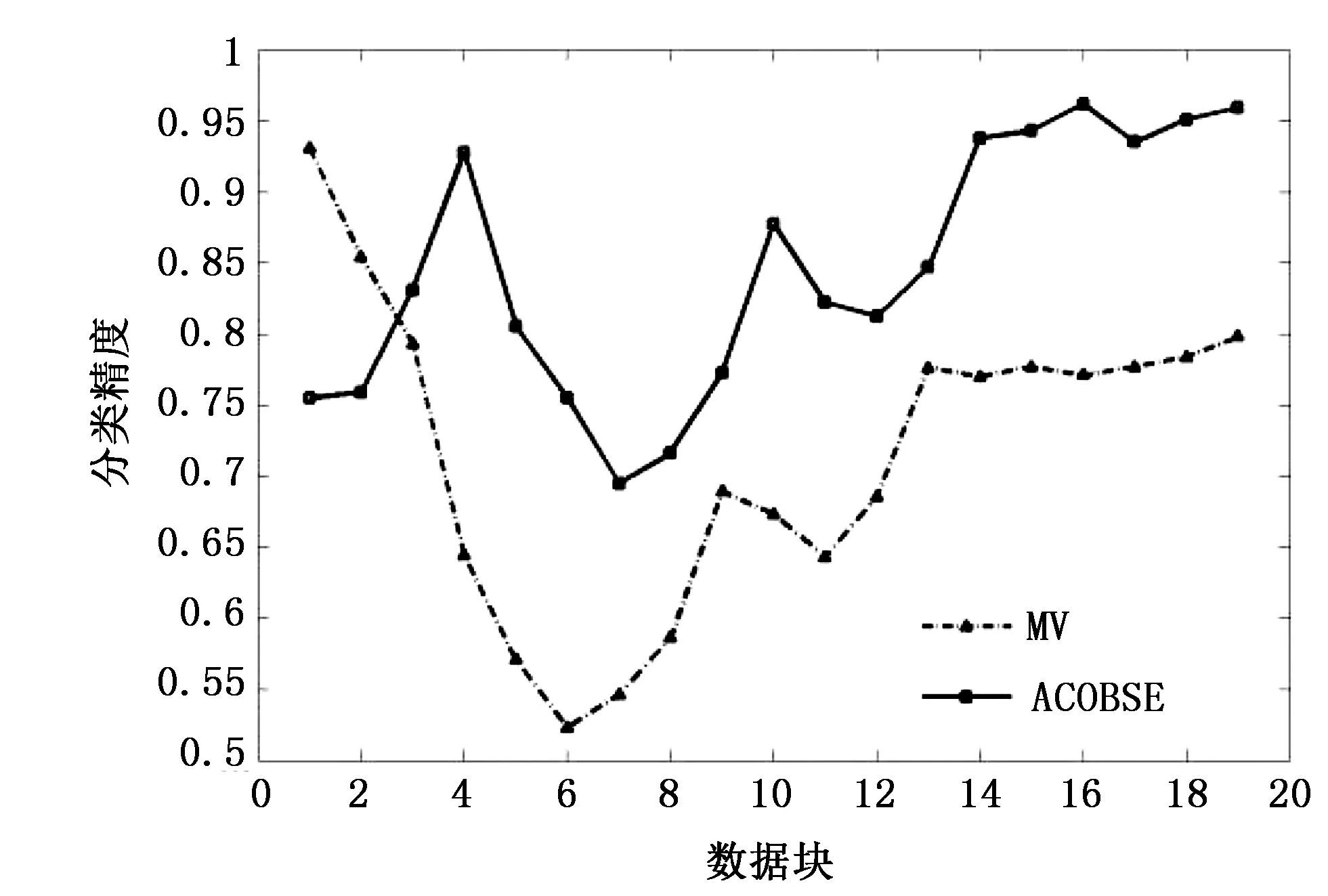
图2 数据集H0(不含噪声)试验结果

仿真试验基于WEKA平台在Eclipse环境下完成，在标准仿真数据集上进行试验。同时结合现有文献采用基于准确率选择集成的简单投票方法(Majority Voting，MV)与该集成分类算法进行对比。试验采用Bayes学习器作为基分类器，采用BatchMode训练生成，其中数据块大小为1000个样本，首先训练40个基分类器，采用10折交叉验证得出各基分类器的分类精度，集成规模定为20。2种集成分类模型在3个数据集上分类情况分别如图2～图4所示。 从图2～图4可知，基于蚁群优化的选择性集成方法是可行的的，分类准确率比基于传统准确率选择性集成方法要好。这主要是因为ACOBSE方法用基分类器的分类精度作为信息素浓度，利用蚁群优化算法构建集成模型时，挑选的是分类精度相对较高的基分类器，提高了集成分类模型的预测精度。与此同时，当数据流含有噪声时，ACOBSE算法的分类精度起伏程度相比基于准确率动态集成方法要低(见图3和图4)，说明ACOBSE方法能更好地应对概念漂移的发生，只有当数据流中概念漂移达到一定程度之后才会对集成模型的分类精度带来影响，即算法具有良好的鲁棒性。当概念漂移发生之后，ACOBSE方法分类曲线图出现低峰，但能够快速恢复其识别准确率，且分类精度下降幅度比MV方法小，说明ACOBSE方法能够很好地适应概念漂移，能够及时捕捉、快速适应概念漂移的出现，使集成模型保持正常分类水平。ACOBSE方法在构建集成分类模型时，用分类器差异性作为基分类器挑选标准之一，保持基分类器之间的多样性，使集成模型具有良好的泛化能力，这也是该算法在分类初期预测效果一般，而一旦发生概念漂移该算法的分类精度要明显优于传统集成方法的主要原因。在数据流包含噪声较高的环境下，ACOBSE算法在进行数据流分类时出现尖峰次数比MV分类方法相比要少(见图4)，而且尖峰起伏程度相对比较低。每次出现尖峰即是数据流发生概念漂移现象，数据集包含噪声越大发生概念漂移的几率就越大，而ACOBSE方法曲线图中尖峰较少，说明ACOBSE方法比传统集成方法具有更好的稳定性，能够快速适应概念漂移并对数据流中出现的新概念准确分类。这主要是因为ACOBSE方法在挑选基分类器时不仅考虑分类精度，同时把分类器差异性作为衡量标准之一，保持各基分类器之间的多样性，使集成模型面对概念漂移依然具有良好的泛化能力。

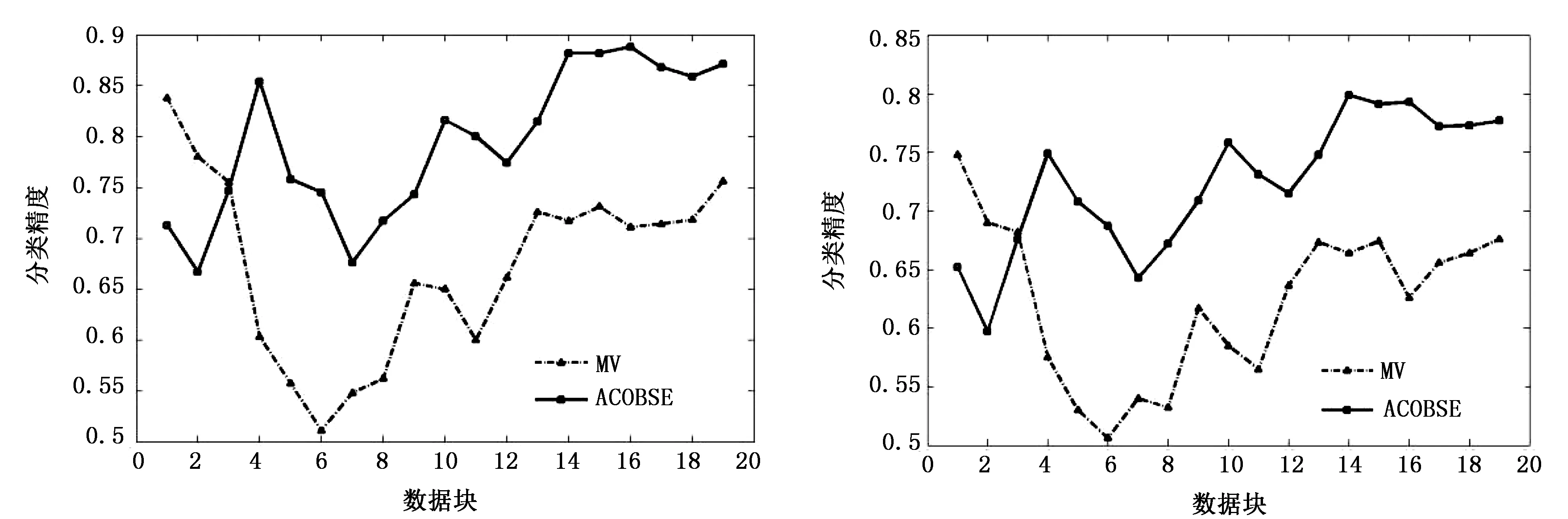
图3 数据集H1(10%噪声)试验结果 图4 数据集H2(20%噪声)试验结果

表3 2种集成模型试验结果

从表3准确率统计分析可知，ACOBSE算法明显优于传统集成方法MV，分类准确率约高出12%，在一定噪声环境下依然拥有较高的准确率，说明ACOBSE算法能较好的应对数据流中隐含的噪声，且快速适应数据流中出现的概念漂移现象。当数据集从不含噪声变成含有噪声数据时，ACOBSE方法的分类精度值下降明显少于MV方法，说明ACOBSE方法在面对含有噪声的数据时稳定性更好，具备较强的抗噪特点。因为ACOBSE方法在构建集成模型时，用分类器之间的差异性作为挑选标准之一，保持集成分类模型中分类器之间的多样性，使集成模型面对隐含噪声和概念漂移的数据流依然具有良好的分类准确率和泛化能力。与此同时，ACOBSE方法构建的集成模型分类稳定性相对传统MV方法较好，在一定噪声环境下依然能够准确对数据流进行分类，且随着噪声的增加ACOBSE方法依然表现出较好的稳定性，说明该算法具有较强的鲁棒性。

综上所述，基于蚁群优化算法的选择性集成数据流分类方法是可行的，能够挑选出性能优良的基分类器构建集成分类模型。

5 结语

针对动态数据流分类问题，笔者提出并实现了一种基于蚁群优化的选择性集成方法。该算法不仅考虑基分类器的分类精度，同时计算分类器之间的差异性，最终挑选的基分类器不仅具有良好的分类精度，同时保持一定差异性，这也是算法在噪声环境下保持分类稳定性的关键因素。仿真试验表明，基于蚁群优化的选择性集成数据流分类方法在分类精度和稳定性方面均有不错效果，是一种可行的数据流分类方法。然而实际数据流中大量数据是无标签的样本，因此如何在具有不完全标记的数据流环境下或样本不平衡条件下，基于主动学习和半监督学习技术设计数据流的概念漂移检测与分类方法是后续的主要研究内容。

[1]Dietterich T G. Machine learning research:four current directions[J]. AI Magazine, 1997, 18(4):97～136.

[2]Street W N, Kim Y S. A streaming ensemble algorithm (SEA) for large-scale classification[A] .ACM SIGKDD International Conference on Knowledge Discovery & Data Mining[C]. 2001:377～382.

[3]Wang H, Fan W, Yu P S, et al. Mining concept-drifting data streams using ensemble classifiers[A] .ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].2003:226～235.

[4]Farid D M, Zhang L, Hossain A, et al. An adaptive ensemble classifier for mining concept drifting data streams[J]. Expert Systems with Applications, 2013, 40(15):5895-5906.

[5]毛莎莎, 熊霖, 焦李成,等. 利用旋转森林变换的异构多分类器集成算法[J]. 西安电子科技大学学报(自然科学版), 2014, 41(5):48～53.

[6]Liao J W, Dai B R. An ensemble learning approach for concept drift[A] .International Conference on Information Science and Applications (ICISA)[C]. 2014:1～4.

[7]Gogte P S, Theng D P. Hybrid ensemble classifier for stream data[A].International Conference on Communication Systems and Network Technologies (CSNT)[C]. 2014:463～467.

[8]邹权, 宋莉, 陈文强,等. 基于集成学习和分层结构的多分类算法[J]. 模式识别与人工智能, 2015, 28(9):781～787.

[9]王中心, 孙刚, 王浩. 面向噪音和概念漂移数据流的集成分类算法[J]. 小型微型计算机系统, 2016, 37(7):1445～1449.

[10]Colorni A, Dorigo M, Maniezzo V. Distributed optimization by Ant Colonies[A] .Ecal91-European Conference on Artificial Life[C]. 1991.

[11]夏小云, 周育人. 蚁群优化算法的理论研究进展[J]. 智能系统学报, 2016, 11(1):27～36.

[12]Zhou Z H, Wu J X, Tang W. Ensembling neural networks: many could be better than all[J]. Artificial Intelligence, 2002, 137(1-2):239～263.

[13]赵胜颖, 高广春. 基于蚁群算法的选择性神经网络集成方法[J]. 浙江大学学报(工学版), 2009, 43(9):1568～1573.

[14]Liu L, Wang B, Zhong Q, et al. A selective ensemble method based on K-means method[A] .International Conference on Computer Science and Network Technology[C].2015:665～668.

[15]Liu L, Wang B, Yu B, et al. A novel selective ensemble learning based on K-means and negative correlation[M].Cloud Computing and Security,Springer International Publishing, 2016.

[16]张春霞, 张讲社. 选择性集成学习算法综述[J]. 计算机学报, 2011, 34(8):1399～1410.

[17]刘余霞, 吕虹, 刘三民. 一种基于分类器相似性集成的数据流分类研究[J]. 计算机科学, 2012, 39(12):208～210.

[18]Hulten G, Spencer L, Domingos P. Mining time-changing data streams[A].Acm Sigkdd Intl Conf on Knowledge Discovery & Data Mining[C]. 2001:97～106.

[编辑] 洪云飞

2016-12-10

国家自然科学基金项目(61300170)；安徽省自然科学基金项目(1608085MF147)；安徽省高校省级优秀人才重点项目(2013SQRL034ZD)。

王军(1992-)，男，硕士生，现在主要从事机器学习、数据挖掘方面的研究工作。

刘三民(1978-)，男，博士，副教授，现主要从事模式识别、机器学习、数据挖掘方面的教学与研究工作，aqlsm@163.com。

TP391

A

1673-1409(2017)05-0037-07

[引著格式]王军，刘三民，刘涛.基于蚁群优化的选择性集成数据流分类方法[J].长江大学学报(自科版)，2017,14(5)：37～43.