新型终端滑模观测器在PMLSM中的应用

张 博，齐 蓉

(西北工业大学,西安710129)

0 引 言

永磁直线同步电动机(以下简称PMLSM)因其简单的定子和动子结构,近年来在自动化数控机床、工业机器人等精密直线传动伺服控制领域得到广泛应用。与传统的旋转电机-丝杠的直线驱动方式不同,PMLSM能够将电能直接转换为直线运动,省去了中间转换的传动环节,因而具有推力大、响应速度快、效率高、传动损耗低以及无齿隙啮合问题等优点[1-3]。在高精度的PMLSM控制中,通常采用精确度高的光栅尺完成对磁极位置检测、速度检测和系统定位等功能。然而,安装光栅尺对使用环境、安装面等要求较高,并且系统的成本和复杂性会因光栅尺的使用而增加,系统可靠性也会随之降低。因而,采用无位置传感器技术实现位置和速度的估计已成为PMLSM控制研究的一个热点[3-5]。

无位置传感器方法的主要思想是对电机绕组中的电压和电流信号进行适当的处理,随后采用合适的算法对位置进行估计,主要包括信号注入法和观测器估计法2类。文献[6-7]采用高频信号注入法实现了在低速或全速运行下同步电机的位置估计,这种方法对电机参数的变化不敏感,对凸极效应明显的PMLSM的初始位置估算较为准确,但对于隐极式或表贴式PMLSM位置估算精确度并不理想。相比而言,采用观测器方法无需额外的硬件系统就能实现PMLSM的无位置传感器的位置和速度的估计。传统观测器设计又可分为卡尔曼滤波方法、反电动势积分法和滑模观测器方法等。文献[3,8-12]的设计思想主要是基于扩展卡尔曼滤波算法或Unscented卡尔曼滤波算法,实现PMLSM的无位置传感器控制,此方法具有较宽的调速性能且对控制系统噪声的抑制较为有效。然而,采用的迭代算法会加重计算负担,同时也易受系统模型参数的影响。文献[13-14]采用了反电势积分法实现同步电机的位置、速度估计,但积分漂移和稳态误差问题较难解决。此外,文献[15]提出采用非线性观测进行估计,对于要求不高的伺服系统可满足,但对于精度要求较高的系统却无法满足。

滑模观测器法凭借简单的滑模算法,对电机参数的要求不高,具有较强的鲁棒性能,在同步电机无位置控制中脱颖而出。但其本质上是不连续的开关控制,容易引发系统抖振现象,进而影响系统的稳态精度。为了更好地应用滑模方法设计观测器,常规的一阶滑模观测器的设计是将电流估计值与实测电流值的误差来估计反电动势,并采用边界层法,即连续函数或饱和函数代替滑模面的符号函数的方法来削弱滑模抖振对估计值的影响。文献[16]在边界层法的基础上,引入低通滤波器的设计,进一步降低高频抖振,但加入低通滤波器会带来相位滞后,相位补偿角会使计算量增大。为了避免设计低通滤波器带来的影响,文献[1]提出了反电动势观测器的设计,并证明了观测器的渐近稳定性,但估计值的稳态精度仍然无法保障。文献[17-19]将高阶滑模的控制方法引入到观测器的设计中,不仅能够有效地消除滑模的固有抖振,而且避免了外加滤波器引起的估计误差,然而,将高阶滑模控制方法应用于PMLSM无位置传感器控制系统却报道较少。

本文将高阶滑模理论和非奇异终端滑模有限时间收敛特性相结合,提出一种比例-积分(PI)型二阶非奇异滑模观测器的设计方法。采用二阶非奇异终端滑模目的在于消除抖振并保证有限时间内收敛,引入PI算法旨在进一步提高系统的精度,降低估计值的稳态误差。同时,引入锁相环(phaselocked loop,PLL)技术,实现了PMLSM的位置和速度的在线估计。最后,在PMLSM矢量控制平台上,分别采用2种典型的传统滑模方法和本文方法进行实验测试,结果验证了本文提出的方法可有效地提高PMLSM无位置控制系统位置和速度估值精度。

1 PMLSM的数学模型

对于面装式PMLSM,假设定子绕组对称分布,空间磁场正弦分布,绕组上施加对称3相电压,忽略磁路饱和,不计涡流和磁滞损耗,在d-q坐标系下,综合PMLSM动力学方程和电压方程,PMLSM的数学模型可描述[20]:

式中:x,v分别为PMLSM的动子位移和速度;kf为推力系数;m为动子质量;fv为粘滞系数;Ffric为运动中的PMLSM所受的摩擦力;Fripple为由PMLSM的结构引起的波动力,包括齿槽力和边端力,可视为极距τ的正弦函数;Fl为外部负载力,ΔF为系统中由不确定性因素引起的扰动力;id,iq分别为直轴和交轴电流;ud,uq分别为直轴和交轴电压;L为定子绕组电感;R为定子上的绕组电阻;ωe为PMLSM动子的运动折算成的电角度,它与动子运动速度v、永磁体极距τ和极对数p相关且ωe=pπv/τ;φf为永磁体磁链。

为了方便分析,以PMLSM的定子电流作为状态变量,在两相静止α-β坐标系下,式(1)的电压方程及反电动势可表示:

式中:θe为 PMLSM 等效的电角度且 θe=pπx/τ;iα,iβ分别为α轴和β轴的定子绕组电流;L0,R0分别为PMLSM绕组的电感和电阻的名义值;eα,eβ分别为α轴和β轴的反电动势,uα,uβ分别为α轴和β轴的定子电压。

2 新型二阶终端滑模观测器

PMLSM位置和速度的全部信息可由式(2)的反电动势方程导出。因而,位置和速度估计值的准确性主要取决于反电动势的估计结果。

2.1 传统滑模观测器设计

设定子电流为状态量,则根据式(2)的电压方程,常规滑模观测器可设计[2,21]:

式中:用“ ^”表示观测值,^的估计值,

令式(3)减去式(2),得电流观测器的误差方程:

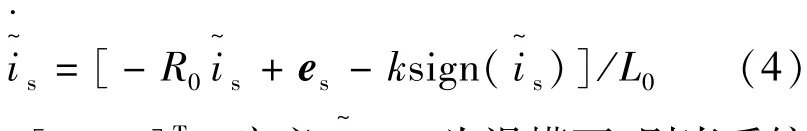
由式(5)可知,电机的反电动势估计值可由一个含有符号函数的表达式表示,因为符号函数是不连续的,因而必然含有高频分量。为了获得较为平滑的反电动势估计值,可外加低通滤波器滤除高频分量,这会引入相位延迟,需设计相位补偿方法,则经滤波处理后的反电动势、位置及速度的估计值如下:

式中:ωc表示低通滤波器的截止频率。

由式(6)可以看出,截止频率的选择对反电动势估计值的影响较大,且不能完全消除滑模抖振。

针对上述问题,常用的方法,如文献[2]采用边界层对滑模方法进行了改进,即将符号函数用连续函数替换。连续函数:

式(7)中,a的值可调。同时,因PMLSM的速度的变化远低于定子电流,故可假设=0,则由式(2)的反电动势方程,得:

因而,反电动势观测器的设计可由式(8)推出,如下:

式(9)中,观测器增益l＞1;将式(9)减去式(8),得反电动势误差观测器:

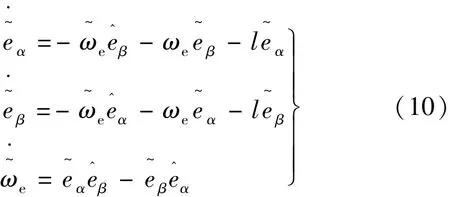
根据李雅普诺夫的稳定性原理,可知,式(10)的反电动势误差观测器渐近稳定。因而,采用这种方法能够避免因低通滤波器所带来的相位补偿问题,但因观测器是渐近稳定的,其精度无法保证。

2.2 二阶PI型非奇异终端滑模观测器设计

由非奇异终端滑模理论[22]可知,采用这种滑模方法,系统具有可达性,并随后在有限时间内滑模变量及滑模变量速度均能收敛为零,从而从根本上解决了系统的跟踪精度问题。又根据高阶滑模原理可得,高阶滑模能够抑制低阶滑模的抖振。为此,根据式(3),以定子电流为状态量,本文设计的滑模观测器:

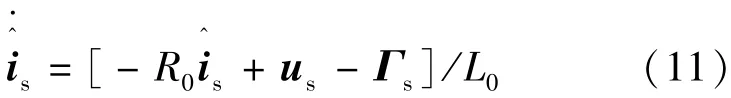
式中,Γs=[Γα,Γβ]T,为滑模控制律。

式(11)与式(2)相减,则滑模观测器的误差方程:

PI型辅助滑模面可定义:

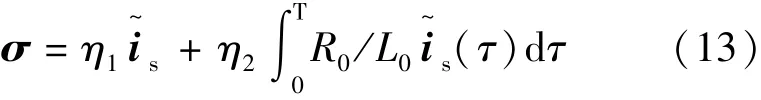
式中:σ=[σα,σβ]T;η1为辅助滑模面的比例系数;η2为积分系数,且 η2＞0。

联立式(11),则设计的二阶非奇异终端滑模面:

式中:λ＞0,p,q均为大于0 的奇数,且1＜p/q＜2,s=

为保证所设计的滑模观测器的稳定性,需根据所设计的二阶滑模面确定滑模控制律,本文设计的滑模观测器的控制律:

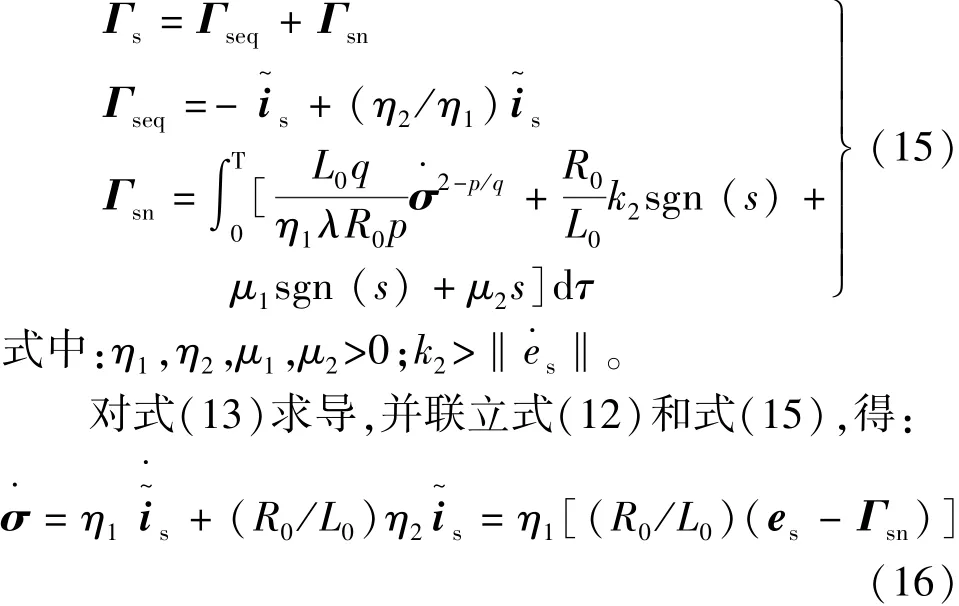
为检验滑模观测器的稳定性,取李雅普诺夫函数求导并根据式(16),有:

讨论:由于λ＞0,p,q均为大于0的奇数,且1＜p/q＜2。 因此,当且仅当 σi=0 时,从而可则在滑模变量 si≠0 时,在下列2 种情形:a)。 故所设计的滑模观测器是稳定的,且能使在有限时间里可达,并随后在有限时间内收敛到零,有;故联立式(12),反电动势可由滑模控制律表示:

注:式(15)的滑模控制律是将符号函数进行了一阶积分运算得来,故实现了对滑模抖振的抑制。同时,由式(13)的PI型辅助滑模面定义可以看出,所设计的滑模观测器通过比例系数η1和积分项系数η2的适当选取,其观测精度与响应速度均可得到提高。

2.3 位置和速度的估计

上节主要是对PMLSM的反电动势估计设计;而要将电机的速度和位置信息从反电动势估计值中精确提取,可采取锁相环技术[18]。锁相环的原理如图1所示。

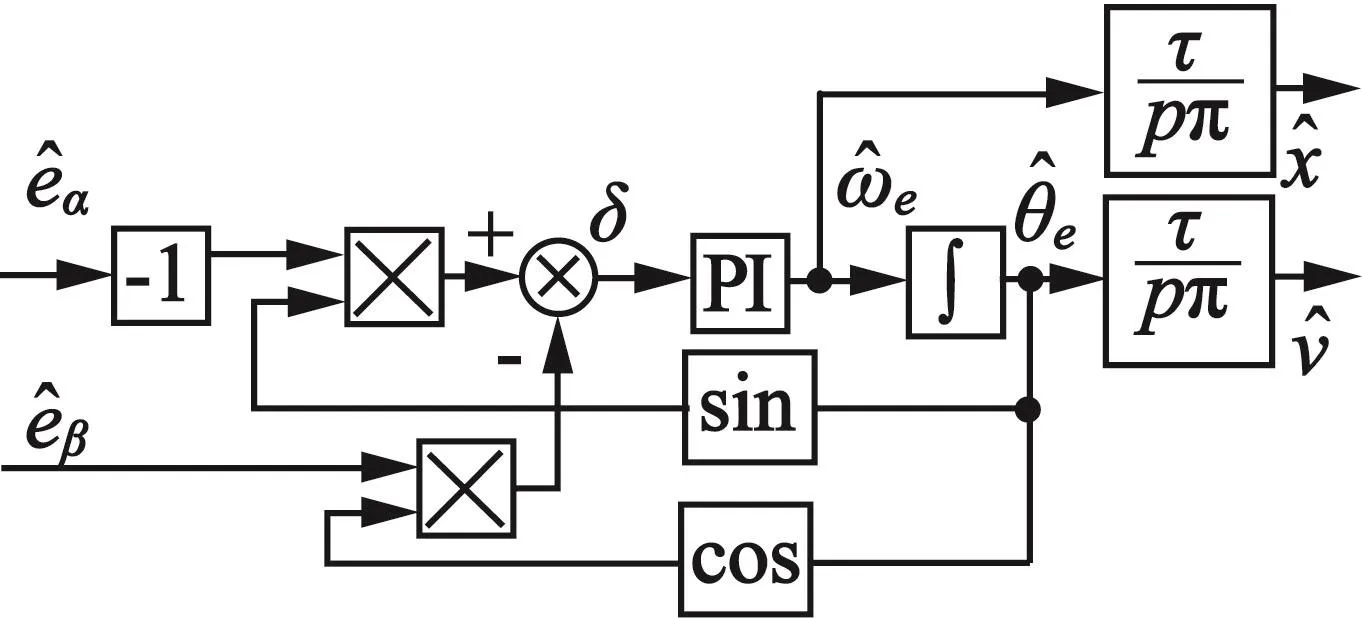
图1 PMLSM锁相环原理设计图

当采用本文提出的滑模观测器,在系统稳定后,滑模控制律Γs可准确地表示电机的反电动势。设反电动势的幅值为γ,则有根据锁相环原理,有:

因此,调节锁相环中的PI参数,总能使δ=0,即PMLSM的实测电角度与估计值相等,从而可实现PMLSM位置和速度的准确估计。

3 实验测试

3.1 实验平台介绍

为了验证所提方法的有效性,本文采用id=0的速度-电流双闭环的矢量控制策略,其原理如图2所示。

图2中,为了提高PMLSM系统的伺服精度和抗干扰能力,速度环控制采用的是比例+微分(PD)算法,而电流环控制采用的是比例+积分(PI)算法;图2中的双闭环控制算法、观测器、锁相环及其他变换算法等是在 TI公司的32位浮点型 DSP芯片TMS320F28335上实现的;DSP输出的6路频率可变的PWM调制波用以调节电机驱动器的输出功率;逆变电路采用的是三菱公司的PS21867智能功率模块,直流母线为8 V,6路IGBT的开关频率设定为1 kHz;PMLSM的a,b两相的相电流选用LEM公司的LTS25-NP霍尔型电流传感器检测。电机实际运行位置和速度采用的光栅尺进行测量,选用雷尼绍公司的RGH22B05L00型光栅尺;实测的位置和电流数据通过数据采集卡输入到PC机上,在PC机上实时运算。试验电机为自主研发的PMLSM,主要标称参数:R0=7.2 Ω;L0=2.89 mH;τ=16 mm;p=3;fv=10.12 N·s/m;φf=0.047 Wb;m0=6.7 kg;kf=61N/m·s-1;ke=26.9 V/m·s-1;电机行程为210 mm;电机额定电流IN=10.1 A。图3为试验电机及DSP单元。

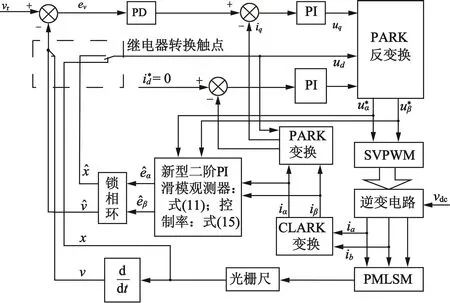
图2 基于id=0的PMLSM无位置传感器矢量控制系统图

图3 试验电机及DSP单元

3.2 实验过程及结果分析

a)实验过程

实验中,可利用DSP的输出通道控制继电器的转换触点(如图2所示),从而方便PMLSM在有位置传感器和无位置传感器中切换。给定速度信号为幅值5mm,频率为0.3Hz的正弦信号:vr=5×sin(0.6πt),实验开始时,先将系统切换到带光栅尺的矢量控制中运行,并经数据采集卡读到PC机上,可测得位置和速度值。当PMLSM运行稳定后,再迅速切换到无位置传感器控制系统中运行,并在DSP中计算速度和位置的估计值。经反复实验测试,速度控制器的P,D参数设定:vp=100,vd=50;交轴电流控制器的P,I参数设定:Ip=2.5,Ii=0.12;直轴电流控制器的P,I参数设定为:Ip=8.1,Ii=4.9。按照式(15)所设计的反电动势滑模观测器控制律参数为:η1=135,η2=9.6,p=7,q=5,λ=0.001,μ1=180,μ2=18 500,k2=0.3。锁相环中的 P和 I的参数调整:kp=21,ki=0.01;并与2种常规一阶滑模观测器方法进行对比实验:式(6)的外加低通滤波器法和式(7)～式(10)的边界层方法。设计常规滑模观测器的参数:k=140;低通滤波器的截止频率设计值:ωc=12 000 rad·s-1;边界层法的参数设计值:α=l=2。当选用这2种方法时,矢量双闭环控制系统控制器的参数不变。

b)实验结果

对采用本文所提方法及文中提到的2种常规滑模观测器设计方法进行对比测试,图4为应用文中3种滑模观测器的位置估算的测试结果。

图4 测试3种滑模观测器的位置估计值

图4 (a)为应用2种传统一阶滑模器方法和本文提出的二阶滑模观测器方法实现电机位置估计的输出结果;图4(b)为由光栅尺测量的位置信号与文中3种滑模观测器估计的位置信号的误差。从图4(a)可得,本文提出的位置估计值与实际测试的位置给定信号最为接近,且抖振更低;从图4(b)可得:采用本文的方法,位置估计值中抖振最低,且估计误差不超过±1 mm,而采用其他2种常规滑模观测器后,位置误差超过±3 mm。因而,应用本文方法对位置估计,精度较高且抖振较低。

图5为应用文中3种滑模观测器的速度估算的测试结果。

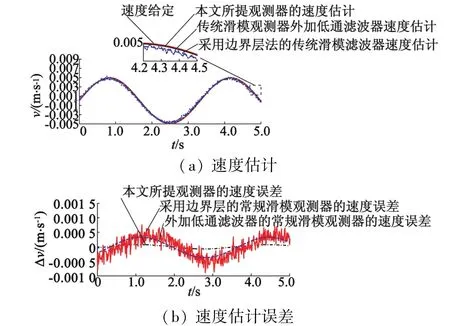
图5 3种滑模观测器对速度估计的测试结果

从图5(a)和图5(b)的测试结果可以看出:与应用常规滑模观测器方法相比,应用2种常规滑模观测器方法,速度估计误差绝对值的最大值大于0.25 mm·s-1,而采用本文提出的方法测得的速度估计的误差值为±0.05 mm·s-1;且应用本文所提方法的速度估计值更加平滑,速度估计值精度更高。

根据给定的速度信号和电机反电动势系数,易得理想的反电动势信号;而采用本文提出的反电动势估计值可由DSP计算得出。在两相静止坐标αβ坐标系下,PMLSM反电动势理想值和采用本文方法设计估算的反电动势结果如图6所示。

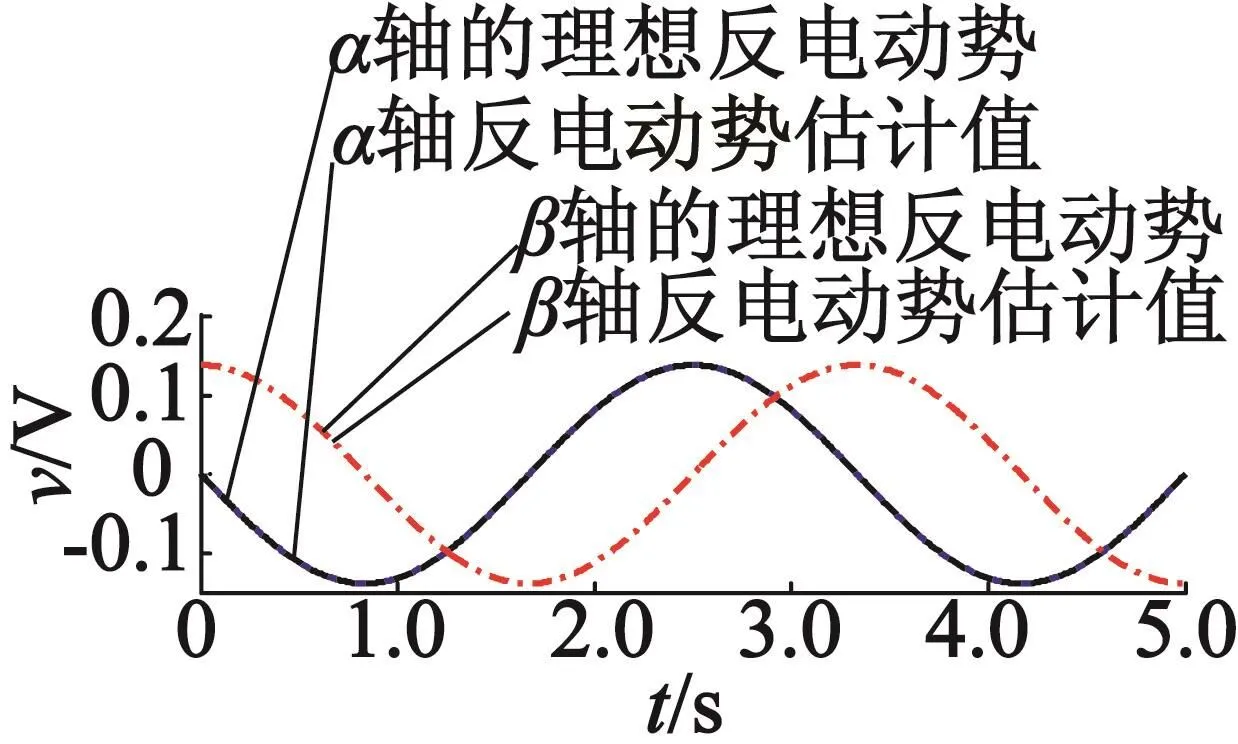
图6 反电动势的理想值和估测值

由图6可知,采用本文提出方法估算的反电动势值与理想的反电动势值一致,因而本文设计的滑模观测器精度较高。

4 结 语

针对高精度PMLSM无位置传感器矢量控制,本文在传统滑模观测器的分析基础上,提出了基于比例-积分算法的二阶非奇异终端滑模观测器,实现了电机反电动势估计,设计该观测器能够从根本上解决传统一阶滑模观测器引起抖振较大的问题;并应用锁相环技术,从反电动势的估值中提取PMLSM位置和速度信号。这种设计方法避免了因外加低通滤波器带来的相位补偿和应用边界层法带来的估计精度变差的问题。实验测试结果反映了本文所设计的滑模观测器能够实现电机反电动势、位置和速度估计值较高精度估算,为PMLSM无位置传感器控制的实现提供了一种有效方法。

参考文献

[1] KAZRAJI S M,SOFLAYI R B,SHARIFIAN M B B.Sliding-mode observer for speed and position sensorless control of linear-PMSM[J].Electrical Control&Communication Engineering,2014,5(1):20-26.

[2] KAZRAJI S M,SHARIFIAN M B B.Direct thrust force and flux control of a PM-linear synchronous motor using Fuzzy Sliding-Mode Observer[J].Recent Advances in Electrical&Electronic Engineering,2015,13(1):9.

[3] 余佩琼,陆亿红,王涌,等.永磁直线同步电动机无位置传感器控制系统的研究[J].中国电机工程学报,2007;24(27):53-57.

[4] 陆华才,徐月同,杨伟民,等.无位置传感器表面式永磁同步直线电机初始位置估计新方法[J].中国电机工程学报,2008;28(15):109-113.

[5] 王利,卢琴芬,叶云岳.永磁直线同步电机无位置传感器动子位置辨识[J].电机与控制学报,2012,16(6):7-12.

[6] 秦峰,贺益康,刘毅,等.两种高频信号注入法的无传感器运行研究[J].中国电机工程学报,2015,25(5):116-121.

[7] LU H C,YAO X Y,TI J.Combined back-EMF estimator with high-frequency signal injection for wide speed range sensorless control of PMLSM[J].Advanced Materials Research,2013,753-755(16):1405-1408.

[8] 余佩琼,王涌,杨伟民,等.UKF在永磁直线同步电动机无位置控制中的应用[J].机械工程学报,2007,43(11):149-153.

[9] 余佩琼,陈子辰.基于UKF的永磁直线同步电机进给系统位置与速度估计[J].电工技术学报,2007,22(9):56-61.

[10] 陆华才,徐月同.基于AEKF的永磁直线同步电机速度和位置估计算法[J].中国电机工程学报,2009,29(33):90-94.

[11] YANG W M,PAN L J,P F,et al.Applications of extended Kalman filter for position sensorless control of permanent magnet linear synchronous motor[J].Advanced Materials Research,2013,834-836:1240-1245.

[12] ARUNDHATI B,MARY K A,RAGHAVENDR T,et al.Sensorless speed control of permanent magnet linear synchronous motor using extended Kalman filter[J].Journal on Electrical Engineering,2014:20-24.

[13] LU Huacai,LI Manhua,XU Yuetong.Sensorless position and speed estimation with improved integrator for PMLSM drive[C]//International Conference on Information and Automation,2009:380-384.

[14] 李彪,李黎川.基于高性能磁链算法的永磁同步电动机无位置传感器控制[J].电工技术学报,2016,31(11):59-67.

[15] 陆华才,江明,陈其工.采用非线性观测器的PMLSM无位置传感器控制[J].电机与控制学报,2011,15(8):29-33.

[16] DHAMO L,SPAHIU A.An improved performance of sensorless PMSM drive control with sliding mode observer in low speed[J].Ijettjournal Org,2013,4(5):2205-2211.

[17] 郑雪梅,李秋明,史宏宇,等.用于永磁同步电机的一种非奇异高阶终端滑模观测器[J].控制理论与应用,2011,28(10):1467-1472.

[18] 张晓光,孙力,陈小龙,等.基于二阶滑模观测器的永磁同步电机无位置传感器控制[J].电力自动化设备,2013,33(8):36-41.

[19] 袁雷,沈建清,肖飞,等.插入式永磁低速同步电机非奇异终端滑模观测器设计[J].物理学报,2013,62(3):37-45.

[20] WANG M,LI L,PAN D,et al.High-bandwidth and strong robust current regulation for PMLSM Drives considering thrust ripple[J].IEEE Transactions on Power Electronics,2015,31(9):6646-6657.

[21] 陆华才,提娟,刘怡君,等.基于模糊滑模观测器的PMLSM无传感器控制[J].信息与控制,2016,45(1):60-65.

[22] 冯勇,鲍晟,余星火.非奇异终端滑模控制系统的设计方法[J].控制与决策,2002,17(2):194-198.