星光导航大气折射模型及数据模式研究*
2017-05-13武鹏飞宋峰魏合理
武鹏飞,宋峰,魏合理
(1. 中国科学院安徽光学精密机械研究所 中国科学院大气成分与光学重点实验室, 安徽 合肥 230031; 2. 北京电子工程总体研究所, 北京 100854)
星光导航大气折射模型及数据模式研究*
武鹏飞1,宋峰2,魏合理1
(1. 中国科学院安徽光学精密机械研究所 中国科学院大气成分与光学重点实验室, 安徽 合肥 230031; 2. 北京电子工程总体研究所, 北京 100854)
星光大气折射模型及大气数据模式是整个星光折射自主导航方案中的一个重要组成部分。利用光线追迹方法,建立了一种考虑大气空间不均匀性的星光大气折射模型,模型数据基础为自主建立的基于实测廓线数据的全球范围三维空间格点化大气参数廓线模式。同时分析了新建立的星光折射模型与基于单点大气密度指数高度分布的传统星光折射模型之间的差异,相对于传统模型,新模型由于考虑了大气不均匀性,理论精度更高。
星光导航;折射模型;大气不均匀性;大气模式;格点;大气廓线
0 引言
星光折射自主导航是开展研究较为广泛的一种天文导航技术,在高空长航时的光电系统上的应用前景是广阔的,其具有误差不随时间积累、导航精度较高、不依赖地面站、在电磁环境下抗干扰能力强以及可同时提供位置和姿态信息等特点[1-3]。
星光大气折射模型及大气数据模式是整个星光导航方案中一个重要组成部分,其准确度是影响星光折射导航定位精度的重要因素之一。目前采用较多的星光折射模型基于大气密度随高度指数分布的假设[4-5],虽形式简单,但当该假设不成立时将会产生较大误差,并且模型中采用的是单点位置的大气廓线数据,不能代表整个长距离光线传输路径中的大气状况。而目前采用的大气廓线模式主要是美国标准大气[6]、国际空间研究委员会(committee on space research, COSPAR)给出的国际参考大气CIRA(COSPAR international reference atmosphere)[7]或美国海军研究实验室(naval research laboratory, NRL)给出的NRLMSISE-00(NRL mass spectrometer and incoherent scatter radar extended)大气经验模式[8]等,实际应用时通常将模式数据随高度分布按照指数函数形式进行拟合。然而,这些大气模式的数据源受限于有限的探测区域和探测时间、较慢的更新速度和时空分辨率不高、精度不明确等缺点,并不完全符合全球局部的实际地理和大气状况,若直接予以采用,则形成的导航方案会受限于上述国外大气模式及其缺点。
因此,考虑到全球局部地理和大气状况的复杂性,必须建立不依赖于大气数据高度分布形式假设的星光大气折射模型,以及配套的在数据积累、统计分析、模式构建、精度分析与验证、更新等方面具有自主可控性的全球较高精度的大气廓线模式,从而确保高精度星光折射自主导航技术的有效性和准确性。
1 传统星光大气折射模型
当星光通过地球大气时,由于地球大气层密度分布的不均匀,光线会首先向地心方向弯曲,然后偏离地心方向向大气层外出射,进入飞行器视线中,这种光线传输方式一般称为地球大气临边传输。如图1a)所示,视线方向距地球表面最近的高度为视高度ha,而实际折射光线距离地表最近的高度称作切点高度ht。星光折射角θR定义为星光入射光线和出射光线的夹角,它反映了光线的偏折程度。
大气参数随高度的分布形式是星光折射理论分析的重要基础,指数分布因其在数学上的简洁性,以及与实际大气密度高度分布较好的一致性在传统星光折射模型的建立上得到了广泛的应用。大气密度指数高度分布一般描述为
ρ=ρoexp[-(h-ho)/H],
(1)
式中:ρ为距地球表面高度h处的大气密度;ρo为参考高度ho处的密度;H为参考高度ho处的密度标高。
依据大气密度指数高度分布建立的传统星光折射角计算公式为[2]
θR,1=k(λ)ρt[2π(Re+ht)/H]1/2,
(2)
式中:k为与光波长相关的Gladstone-Dale常数;Re为地球半径;ρt表切点高度处的大气密度。
依据图1a)星光折射几何关系和式(2)可得到传统星光传输视高度[2]:
ha,1=ho-HlnθR,1+Hln[k(λ)ρo(2πRe/H)1/2]+
θR,1(HRe/2π)1/2.
(3)

图1 星光临边传输大气折射几何示意图Fig.1 Schematic diagram of starlight refraction geometry under limb transmission
在实际应用时,将大气密度模式数据按照切点高度处恒定标高的指数函数形式进行拟合,得到式(3)中的相关参数,然后依据实际测量得到的星光折射角,即可通过反演得到视高度。目前,几种常用的国外大气参数模式(0~120km),如表1所示,国内当前大多星光折射导航方案主要是基于这些大气模式数据[9-10]。
2 基于格点化大气参数模式的星光大气折射模型
如上所述,传统星光折射模型采用的是星光传输过程中单点的大气参数廓线,并且将廓线数据依据指数分布进行拟合,但是考虑到星光实际传输路径较长,覆盖的区域很广,尤其是当切点高度较低时,单点的大气参数廓线并不能代表整个光线传输路径中的大气状况,大气不均匀性的影响将会使传统方法的精度受到限制,并且指数分布假设也与实际大气存在一定差异。因此,高精度星光折射模型必须考虑大气不均匀性,且不依赖于指数高度分布假设。基于此,根据星光、地球及飞行器之间的几何关系和光波传播定律,以及三维空间格点化大气参数廓线模式,建立了基于光线追迹的星光大气折射模型。
2.1 星光大气折射模型
考虑光线向地心方向弯曲的传播轨迹,如图1b)所示。通常根据光波在大气中传输的机理及大气传输路径方程,将大气分成无数的薄球面层,并假设每一球层内具有相同的密度,则光线只在相邻层的界面上发生折射,并遵循Snell折射定律。图1b)中,θi和βi分别为光线在相邻两层界面处的入射角和折射角,ni为大气折射率,hi为地心距。
由图示几何关系可得到进入大气层后整条光线对应的地心夹角

(4)
应用Bouquer公式[11],即在整个传输光线上,光线的切向矢量s(其方向就是光的传播方向)与矢径r的矢量积为常数,即r×ns=const,以及光线Snell折射定律,则可分别得到每界面层对应的入射角和折射角
θi=arcsin(n1h1sinθ1/nihi),
(5)
βi=arcsin(n1h1sinθ1/nihi+1),
(6)
将式(5)和(6)代入到式(4)中可得

arcsin(n1h1sinθ1/nihi+1)],
(7)

表1 几种常用的大气参数模式
则大气折射角表示为
θR=θ′-θ1=θm+1+αm-θ1=


(8)
从图1a)中可以看出,在飞行器上观测到的光线经历了入射到大气层内和从大气层出射的2个对称的过程。当式(8)中取θ1=90°,此时h1即为切点高度ht,从而可得到星光穿越整个大气后进入飞行器视线的总折射角


(9)
依据飞行器视高度和星光切点高度之间的关系,ha≈(nt-1)(ht+Re)+ht,则式(9)变换为


(10)
由式(9)和(10)可以看到,星光总折射角与光线切点高度/视高度及大气折射率的高度分布有关。
星光折射导航中光线实际传输路径较长,其早已偏离了光线与地球切点处的垂直上空。在新模型的折射计算过程中,考虑大气非均匀性产生的影响,结合光线传输路径,不同高度处的大气参数选取不同格点处对应高度上的大气参数值,如图2所示。
采用星光折射角计算式(10),可由实测得到的星光折射角θR,2反演得到光线视高度,表示为

(11)
式中:ni表示某高度hi上的大气折射率值,大气折射率不仅与温度、压强(即大气密度)有关,还与水汽、波长相关。在可见光/近红外波段,考虑水汽、波长的折射率计算公式采用Stone和Zimmerman在2001年对Edlen结果的修正公式[12-13]:
(12)
式中:t为温度;p为气压;e为水汽压;λ为波长。
2.2 全球三维空间格点化大气参数廓线模式
大气参数模式是星光大气折射模型的数据基础。因此,全球格点化大气参数廓线模式的时空分辨率必须以能满足导航定位精度为重要依据。
导航定位精度一般以圆概率误差(circular error probable,CEP)表示,依据CEP与星光临边大气传输视高度误差δha的关系,以及上述建立的星光大气折射模型中视高度和大气折射率廓线模式之间的关系,即可确定当不考虑其他影响导航定位精度的因素时,在满足一定导航定位精度的条件下,大气折射率廓线模式的误差要求。图3给出在不同星光临边传输视高度条件下,不同导航定位精度对应的大气折射模数廓线模式所要满足的误差。仿真计算条件为:中纬度春季,波长550 nm。折射模数N定义为:N=(n-1)×106,n即为折射率。

图2 不同格点不同高度大气参数的选取Fig.2 Selecting process for atmospheric parameters of each point in light path from the corresponding grid

图3 不同导航定位精度对应的大气折射率廓线模式误差Fig.3 Atmospheric refractive index profile error corresp-onding to different navigation and positioning accuracy
可以看到,对于同一导航定位精度,不同视高度下对折射模数模式误差要求不同,且在定位精度较低时差异表现明显,一般情况下,视高度较低时折射模数模式误差要求较松。其中,当导航定位精度为100,50,20 m时,折射模数模式误差约为4%,2%和1%左右。大气折射模数模式误差决定了格点化廓线模式的时空间隔的选取,即同一时空格点内大气折射模数误差不能超过最大限制误差。由于时空格点是横向经度、纵向纬度和时间的三维函数,若三维是相互独立的,则折射模数模式最大误差对于横向纬度、纵向经度和时间三维分别为:1.35%,0.67%和0.33%。
在依据大气折射率模式误差确定经纬空间格点及时间间隔大小后,格点化大气参数廓线模式构建总体流程如图4所示。
首先收集了全球地区的大气实测廓线数据,并形成数据库,主要数据源包括气球探空[14]和卫星观测数据[15],站点尽可能多,覆盖地区尽可能大,数据精度尽可能高,且有长期的数据积累。目前,气球探空是获得中低层高精度大气参数廓线数据(包括温度、湿度和气压等)的主要且最直接的手段,而搭载于美国Aqua卫星上的红外大气探测仪AIRS(atmospheric infrared sounder)、TIMED(thermosphere, ionosphere, mesosphere energetics and dynamics)卫星上的大气探测仪SABER(sounding of the atmosphere using broadband emission radiometry)是目前可获得长期较高精度中高层大气参数廓线数据的仪器。图5是部分全球探空站点地理位置分布示意图。

图4 格点化大气参数模式构建算法流程框图Fig.4 Flow chart of algorithm for constructing gridded atmospheric parameters model

图5部分全球探空站点(红色实点)地理位置分布Fig.5 Part of the global radiosonde (red dot) geographical distribution
然后研究了全球格点化大气参数廓线模式构建算法,主要包括数据质量控制,基于海量数据的统计分析处理,基于稀疏非规则时空数据构建具有一定经纬格点空间分辨率和时间分辨率的大气参数模式的数据同化等。
(1) 数据质量控制
依据NRLMSISE-00大气参数经验模式,将实测廓线数据与经验模式值进行对比,当实测数据与模式值相差较大、超过阈值ξ(h)时,认为该测量数据是异常的,具体有效判断依据表示如下:

(13)
(2) 统计平均分析
对全球实测廓线有效数据进行统计平均,得到平均大气参数廓线,然后依据数据统计特征剔除离群数据。离群数据是与平均值相差较大的数据,采用3倍标准偏差(3σ)作为离群数据的判断依据,即



(14)

(3) 数据同化


(15)


(16)

可以看到,权重函数具有如下特征:权重大小随着站点与分析格点之间的间距变大而变小,即间距近数据的权重大于间距远数据的权重;权重大小随站点量值误差方差的增大而减小,即给予精确数据的权重大于不精确数据的权重;同一站点的权重大小与参数类型有关,而与量值无关。
图6给出依据上述格点化大气廓线模式构建算法,建立的某格点1月中旬的大气参数廓线模式。
3 星光大气折射模型仿真分析
将建立的基于格点化大气参数廓线模式的星光折射模型与传统星光折射模型进行比对,通过数值仿真分析,观察两者的相对偏差。具体仿真条件是:3月中旬,光线传输切点处的经纬度为(0°N, 0°E),沿经度方向传输。视高度为20 km时光线轨迹覆盖的经纬格点和格点间折射模数、温度相对偏差如图7所示。

图6 某格点1月中旬大气参数廓线模式Fig.6 Some atmospheric parameters profile model of one grid in the middle of January
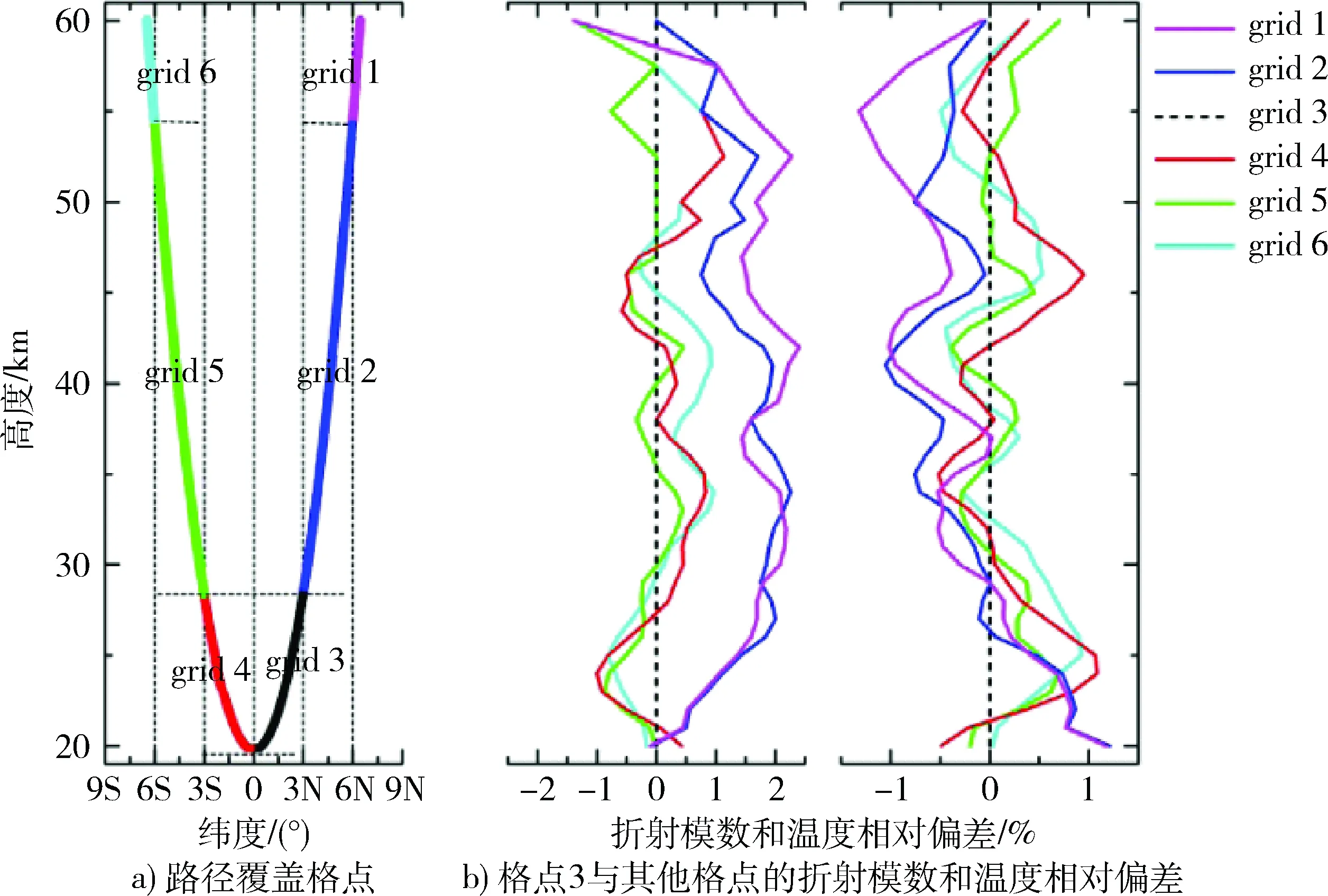
图7 星光传输路径Fig.7 Starlight propagation path
依据星光传输切点处(格点3)的大气密度廓线模式数据,通过指数函数形式拟合得到的传统星光折射模型中需要用到的各项参数,如图8,包括参考高度ho和密度ρo,以及密度标高H。

图8 依据切点处大气密度高度分布数据按指数形式拟合曲线Fig.8 Density vertical distribution of tangent point and fitting curve using exponential function
图9给出在上述仿真条件下,星光折射角为5″~350″时,利用传统星光大气折射模型和新模型分别计算得到的视高度。可以看到,基于格点化大气参数廓线模式的星光折射模型与基于单点指数大气分布的传统折射模型之间存在差别,在上述仿真条件下,相对偏差在10%以内。因此,传统折射模型与基于格点化大气参数廓线模式的星光折射模型相比,存在一定偏差,由于新折射模型考虑了大气的不均匀性,并且不依赖于大气参数高度分布假设,更接近大气真实情况,将会对提高导航定位精度有一定帮助。

图9 采用不同星光折射模型得到的视高度Fig.9 Apparent height obtained by different starlight refraction model
4 结束语
星光折射导航主要是利用大气的光学折射特性,因此飞行器的定位精度依赖于星光大气折射模型的精度以及大气参数廓线模式的准确程度。传统星光折射模型基于一个重要的假设,即大气密度随高度指数递减,其在形式上达到了简洁易用的效果,然而随着对导航定位精度要求的不断提高,其缺点也日益明显。如何建立高精度的星光大气折射模型,满足当前以及未来导航定位精度的要求,是需要解决的一个技术问题。本文重点提出了一个不同于传统折射模型的解决思路,以构建全球三维空间格点化大气参数廓线模式为基础,考虑大气不均匀性,利用光线追迹方法,最终建立了不依赖于大气参数高度分布假设的星光大气折射模型。相对于传统模型,新模型的建立和进一步优化与完善将为提高星光折射导航定位精度提高基础。
[1] CHORY M A, HOFFMAN D P, LEMAY J L. Satellite Autonomous Navigation-Status and History[J]. IEEE Transaction on Position, Location and Navigation Symposium, 1986, 4(7): 110-121.
[2] 刘朝山, 刘光斌, 王新国, 等. 弹载星敏感器原理及系统应用[M]. 北京: 国防工业出版社, 2010. LIU Chao-shan, LIU Guang-bin, WANG Xin-guo, et al. Principle and Application of Missile Borne Star Sensor[M]. Beijing: National Defence Industry Press, 2010.
[3] 宋峰, 张奕群. 星光大气折射观测导航方法可观性研究[J]. 现代防御技术, 2012, 40(2): 65-81. SONG Feng, ZHANG Yi-qun. Research on Observability of Navigation Approach Using Starlight Refraction Measurements[J]. Modern Defence Technology, 2012, 40(2): 65-81.
[4] WANG Xin-long, XIE Jia, MA Shan. Starlight Atmospheric Refraction Model for a Continuous Range of Height[J]. Journal of Guidance Control and Dynamics, 2010, 33(2): 634-637.
[5] NING Xiao-lin, WANG Long-hua, BAI Xin-bei, et al. Autonomous Satellite Navigation Using Starlight Refraction Angle Measurement[J]. Advances in Space Research, 2013(51): 1761-1772.
[6] National Oceanic and Atmospheric Administration, National Aeronautics and Space Administration, and U. S. Air Force.U.S.Standard Atmosphere 1976[M].U.S.,Washington D.C.:Govemment Printing Office, 1976.
[7] REES D, BARNETT J J, LABITZKE K. CIRA 1986, COSPAR International Reference Atmosphere, Part II: Middle Atmosphere Models[J]. Advances in Space Research, 1990, 10 (12): 1-20.
[8] PICONE J M, HEDIN A E, DROB D P, et al. NRLMSISE-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues[J]. Journal of Geophysical Research, 2002, 107 (A12), SIA 15-1-16.
[9] 王国权, 金声震,孙才红,等. 卫星自主导航中25~60公里星光大气折射模型研究[J]. 科技通报, 2005, 21(1): 107-111. WANG Guo-quan, JIN Sheng-zhen, SUN Cai-hong, et al. Study on Model of Starlight Refraction from 25 km to 60 km in Autonomous Navigation for Satellite[J]. Bulletin of Science and Technology, 2005, 21(1): 107-111.
[10] 胡静, 杨博. 一种改进的星光大气折射观测模型[J]. 红外与激光工程, 2009, 38(2): 272-277. HU Jing, YANG Bo. Modified Measurement Model of Stellar Horizon Atmospheric Refraction[J]. Infrared and Laser Engineering, 2009, 38(2): 272-277.
[11] 饶瑞中.现代大气光学[M].北京:科学出版社, 2012. RAO Rui-zhong, Modern Atmospheric Optics[M]. Beijing: Science Press, 2012.
[12] BIRCH K P, DOWNS M J. An Updated Equation for the Refractive Index of Air[J]. Metrologia, 1993,30: 155-162.
[13] BIRCH K P, DOWNS M J. Correction to the Updated Edlen Equation for the Refractive Index of Air[J]. Metrologia, 1994,31: 315-316.
[14] ROCKEN C, ANTHES R, EXNER M, et al. Analysis and Validation of GPS/MET Data in the Neutral Atmosphere[J]. Journal of Geophysical Research, 1997,102 (25): 29849-2986.
[15] REMSBERG E E, MARSHALL B T, GARCIA-COMAS M, et al. Assessment of the Quality of the Version 1.07 Temperature-Versus-Pressure Profiles of the Middle Atmosphere from TIMED/SABER[J]. Journal of Geophysical Research, 2008, 113(17): 1-27.
Atmospheric Refraction Model and Data Mode for Starlight Navigation
WU Peng-fei1, SONG Feng2, WEI He-li1
(1. Chinese Academy of Science, Anhui Institute of Optics and Fine Mechanics, Key Laboratory of Atmospheric Composition and Optical Radiation, Anhui Hefei 230031, China; 2. Beijing Institute of Electronic System Engineering, Beijing 100854, China)
Atmospheric refraction model and data mode are important compositions in the whole starlight autonomous navigation scheme. According to the light tracing method, an atmospheric refraction model considering atmospheric inhomogeneous is proposed. The data base of the refraction model is the global three-dimensional grid atmospheric profile mode based on measured profile data. Additionally, the difference between the new refraction model and the conventional one which is based on the exponential atmospheric profile model at a single point is analyzed. The result indicates that the theoretical precision of the new model is higher than the conventional one for considering atmospheric inhomogeneous.
stellar navigation; refraction model; atmospheric inhomogeneous; atmospheric mode; grid; atmospheric profile
2016-09-25;
2016-12-21 基金项目:有 作者简介:武鹏飞(1987-),男,山东曲阜人。副研究员,博士,研究方向为天文导航、辐射大气传输研究。
10.3969/j.issn.1009-086x.2017.02.002
V249.32+3; V448.22+4
A
1009-086X(2017)-02-0006-08
通信地址:230031 安徽合肥蜀山湖路350号 E-mail:wupengfei@aiofm.ac.cn
