ADC改进模型评估导弹武器系统效能*

夏维，刘新学，孟少飞，范金龙

(火箭军工程大学， 陕西 西安 710025)

ADC改进模型评估导弹武器系统效能*

夏维，刘新学，孟少飞，范金龙

(火箭军工程大学， 陕西 西安 710025)

为更好地评估存在阶段性飞行特征的导弹武器系统整体效能，将传统ADC模型中的可信性(D)分解为主动段、中间段、再入段3个阶段可信性分别的乘积，并从实战对抗出发，引入操作人员能力素质系数K和战场环境影响参数Q，构建了导弹武器系统综合效能评估指标体系，提出了一种新的效能评估模型ADC改进模型。同时根据导弹武器系统的工作原理及作战运用，综合专家打分、层次分析、模糊综合评判、加权求和等方法量化分析了系统的作战效能。通过实例分析验证了该评估方法的正确性和有效性，为今后导弹的设计研发和作战使用提供了科学决策依据。

导弹武器系统；效能评估；ADC改进模型；阶段性特征；模糊综合评判；层次分析法

0 引言

武器系统的效能，是指在特定的使用环境(作战环境、作战任务、编成部署、作战流程以及武器装备性能测试等)和条件下，对武器系统完成给定作战任务(包括时间、空间和数量等)的相符程度(定性与定量相结合，时间、空间、数量、百分比和概率等)。导弹武器系统的效能评估是导弹研发和作战使用中的重大课题，导弹系统的优化组合、部署分配、评判打击目标的威胁程度、开发指控系统软件和论证新武器需求均涉及到对其效能的评估。当前，评估武器系统的效能既可采用专家评定、试验统计或作战模拟等方法，也可采用量化标尺法[1]、ADC法[2-4]、层次分析法[5]、云模型法[6-11]等解析方法。本文从实战对抗的角度出发，在传统的ADC方法中引入操作人员能力素质系数K和环境影响参数Q，并结合导弹飞行的特点，将其划分为主动段、中间段和再入段3个阶段，在评估导弹武器系统效能的过程中对其可信性进行了阶段性地分析和评估，将D分解为3个不同阶段可靠性矩阵的乘积，给出了一种分阶段的改进ADC方法，相较传统ADC方法而言，该方法更符合导弹的作战使用特点，效能评估值也更加客观，具有更好的实用价值。

1 ADC模型基本原理及改进

传统ADC模型[12]中，系统效能(effectiveness,E)是预期一个系统满足一组特定任务要求程度的度量，是系统可用性(availability,A)，可信性(dependability,D)与能力(capability,C)的函数，模型为

E=ADC，

(1)式中：A为系统在执行任务开始时刻，系统处于正常工作或可投入使用的能力；D为在任务开始时刻可用性给定的情况下，系统在使用过程中处于正常工作或完成规定功能的能力；C为在系统处于可用并可信的状态下，系统完成规定作战任务的能力度量。它能较全面地反映武器系统状态随时间变化的多项技战术指标在作战使用中的动态变化与综合作用。

针对导弹武器系统在飞行过程中的阶段性特点，在传统ADC模型中引入人员能力素质K和战场对抗环境因素Q后，效能评估改进模型变为

E=KA(D1D2D3)C(1-Q).

(2)

2 基于ADC改进模型的导弹武器系统效能评估分析

2.1 导弹武器系统工作原理

导弹武器系统可分为火控子系统和导弹子系统2个部分，其中火控子系统由侦察平台、操控平台、发射平台构成。自受领作战任务后，系统于导弹发射前，首先通过侦察平台得到目标位置信息，接着由目标处理平台编辑后发往指挥控制平台，最后将发射指令流转至发射平台并实施操作发射，工作原理如图1所示。

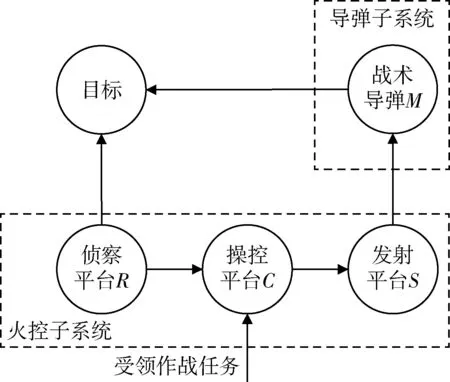
图1 导弹武器系统工作原理图Fig.1 Working principle of missile weapon system

2.2 导弹武器系统效能评估指标体系

通过分析导弹武器系统组成要素及其在执行任务过程各环节中的作用，构建指标体系如图2所示。

评估图2中导弹武器系统的效能主要包括以下几步：导弹发射前系统可用性(A)的评估，也即各系统处于正常状态的概率；系统在导弹发射后至击中目标整个过程中运行状态的可信性(D)度量；系统固有能力(C)的评估度量；使用人员能力素质能力K和战场环境因素Q的确定，最后利用式(2)得到系统的综合效能值，即导弹最终对目标的打击能力的度量。

3 导弹武器系统效能评估

由图1可知，导弹武器系统分为火控子系统和导弹子系统2个部分，而每个子系统又有正常和故障(维修)2种状态，故导弹系统所对应的状态为如下4种：

状态1：导弹子系统正常，火控子系统正常；

状态2：导弹子系统故障，火控子系统正常；

状态3：导弹子系统正常，火控子系统故障；

状态4：导弹子系统故障，火控子系统故障。

3.1 确定系统可用性模型A

武器装备系统的可用性[13]，是指装备在战场环境下使用时，能根据任务需要投入运行的可能性，其指标主要描述系统在开始执行任务时的状态，它是由系统开始处于所有可能状态的概率组成[14]。假设该系统在工作期间的平均无故障工作时间(MTBF)和平均故障修复时间(MTTR)满足指标要求，否则不能保证完成任务，则导弹武器系统的可用性A可表示为

A=(a1,a2,a3,a4),

(3)

式中：a1,a2,a3,a4分别为系统处于状态1～4的概率，也即

A= [aMaH, (1-aM)aH,aM(1-aH),

(1-aM)(1-aH)]，

(4)

式中：aH为火控子系统正常工作的概率；aM为导弹子系统正常工作的概率。

由图1可知，火控子系统由侦察平台、操控平台、发射平台串联组成，故火控子系统正常工作的概率为

AH=aRaCaS，

(5)

式中：aR, aC和aS分别为侦察平台、操控平台和发射平台的可用性。

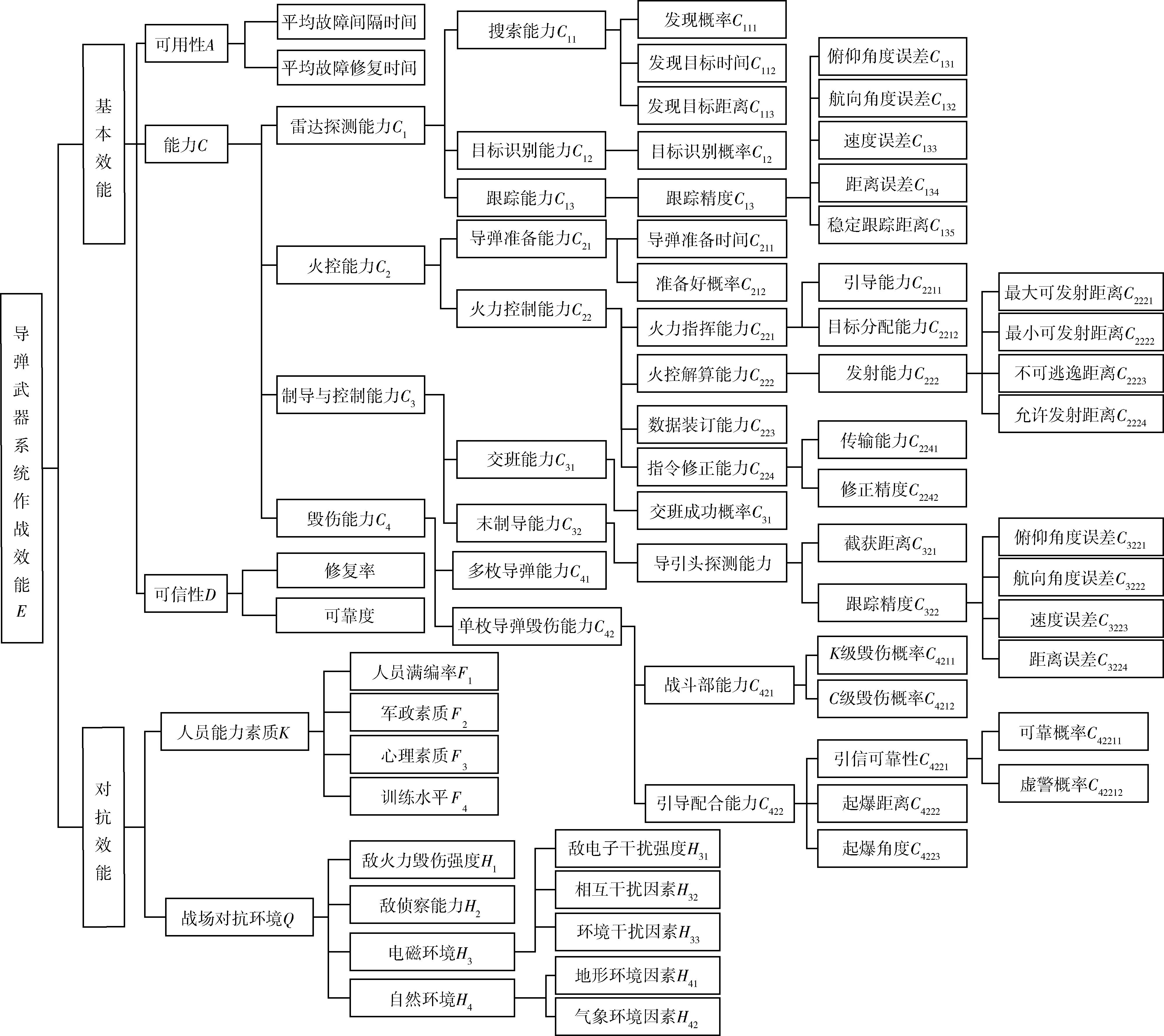
图2 导弹武器系统综合效能评估指标体系Fig.2 Effectiveness evaluation index of missile weapon system

导弹武器系统中，某一环节可能由多个同类型平台并联组成，如多个发射平台共同执行发射任务，其中只要有一个发射设备正常工作，则系统的发射任务就能实现。以m个发射平台共同执行发射任务为例，则其正常工作的概率为

aS=1-(1-aS1)(1-aS2)…(1-aSm),

(6)

式中：aSm为第m个发射平台正常工作的概率。

对于每个基本的武器平台单元，其可用性计算公式为

(7)

式中：MTBF, MTTR为系统平均无故障工作时间和平均故障修复时间。

3.2 确定系统可信性模型D

可信性评估指系统运行时的稳定性，主要描述系统在执行任务过程中的状态。对导弹执行目标打击任务而言，由于导弹发射后仍需要火控子系统的技术支持，故在考虑系统运行的可信性时必须考虑火控、导弹2个子系统的可信性。根据导弹飞行的特点，将其飞行过程分为3个阶段：

主动段——尚未遭受敌武器拦截，影响导弹状态的因素主要是发动机和火控系统故障；

中间段——遭到敌中远程武器拦截；

再入段——遭到敌近程武器拦截(电子干扰或火力拦截)。

3.2.1 主动段可信性评估

设导弹发动机的故障概率为Pf，火控子系统发生故障的概率为Pg，则导弹系统在主动段飞行的可信性为

(8)

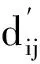
3.2.2 中间段可信性评估

这期间影响导弹系统状态的因素，主要是导弹子系统将面临敌中远程武器的拦截和火控子系统可能遭受的打击。假设导弹的被拦截概率为Pt，火控子系统被敌方破坏的概率为Ph，则导弹系统在中间段飞行的可信性为

D2=

(9)

Pt=1-(1-Pt1)(1-Pt2)…(1-Ptk)，

(10)

式中：Pti(i=1,2,…，k)为第i次拦截武器对导弹的拦截概率。

3.2.3 末段可信性评估

影响导弹在此阶段系统状态的因素主要是敌方所拥有的各种不同类型末段拦截武器的拦截。因导弹已进入末段自导环节，故火控子系统的支持可不予考虑，认为火控子系统始终处于正常状态，也即无论火控子系统是处于正常或故障状态，其向下一个正常状态转移的概率为1，向故障状态转移的概率为0。假设导弹被末段拦截的概率为Pj，则导弹系统在末段飞行的可信性为

(11)

由上分析可知，导弹系统的可信性决定于导弹在3个阶段飞行的可信性，它是一个概率传递的过程，即

D=D1D2D3.

(12)

本文将重点放在考虑对抗环境和人员素质的情况下，分阶段的ADC法研究具体内容，仅考虑导弹在各阶段状态变化的主要概率(发动机故障概率、遭敌方拦截的概率等)，对概率的具体计算方法步骤在此不再赘述。通常情况下，设导弹各分系统的故障时间服从指数分布p=exp(-λT)，λ为系统故障率，详见文献[2-4]。

3.3 确定系统固有能力模型C

能力性评估是对武器系统最终作战能力可达程度的综合评估，导弹系统固有能力主要是指导弹战斗部对目标的毁伤能力。由于导弹在执行任务过程中只有正常和故障2种模式，当系统处于故障状态时，可认为其能力为0，故系统的固有能力矩阵可表示为

C=(c1,c1,0,0)T，

(13)

式中：c1为导弹武器系统正常工作时完成作战任务的概率，它直接体现导弹的综合作战能力。

由图2可知，导弹系统的固有能力向量基本模型主要由雷达探测能力C1、火控能力C2、制导与控制能力C3和毁伤能力C4组成，本文采用层次分析法和模糊综合评判法[15]量化处理能力矩阵C，具体做法如下：

在领域的多元化发展上，华谊兄弟涉及的行业领域种类丰富，不仅在影视娱乐业、艺人经纪上发展较成熟，现在更是朝实体化娱乐和互联网娱乐进行华谊品牌的延伸，具体已有文化主题小镇、电影院以及网络游戏等进展，这些领域为消费者提供选择华谊品牌的更多机会，为华谊品牌市场的拓展注入动力。

Step1根据图2可知，导弹武器系统作战能力评估因素论域U={u1,u2,u3,u4}，式中：

u1={u11,u12,u13}，u2={u21,u22}，

u3={u31,u32}，u4={u41,u42}。

Step2确定评语等级论域V

V={v1,v2,v3,v4,v5,v6,v7,v8,v9,v10,v11}={极好,非常好,很好,好,较好,一般,较差,差,很差,非常差,无}={1.0,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1,0}。

Step3构建因素评判的模糊关系矩阵

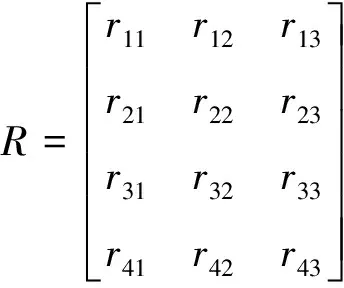
式中：rij为各层评估因素集U中元素Ui对应评语等级论域V中等级Vj的隶属关系，即对评判对象的第i项因素的单因素评判，此处为第一层指标的模糊关系矩阵。

Step5模糊综合评判操作

Step6计算能力值c1

3.4 确定人员能力素质K

该项是指操作人员和指挥人员的综合素质对系统效能发挥的影响，主要由导弹部队人员满编率、使用人员的军政和专业素质、战时心理素质和平时人弹结合训练水平综合决定，如图2所示。因这些指标与系统作战效能正相关，故使用人因素K的表达式为

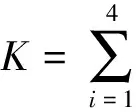
(14)

式中：ωi为由专家打分确定的各项指标权重；Fi为各指标因素在作战中所能达到的程度，用概率的形式表示，其值由上级军事主管部门根据历次军事演习和平时训练考核情况确定。

3.5 确定战场对抗环境因数Q

战场对抗环境因素对导弹武器系统作战效能的影响因环境的不同而互有差异，相同环境中各因素对系统效能的影响也不尽相同。出于普适研究的考虑，图2中给出的是一般的战场对抗环境因素，没有细化到具体的型号、具体的手段和具体的程度。

战场对抗环境因素Q的表达式为

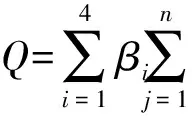
(15)

式中：Hij为战场对抗环境系数的各个因素的具体分值；βi与βij为相应的权重值。

综上所述，将K,Q,A,D,C等的表达式带入式(2)可知，导弹武器系统作战效能为

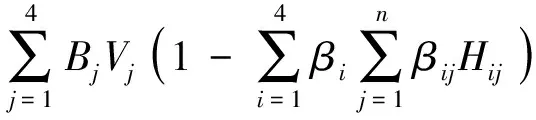
4 实例分析

假设在某次局部对抗作战中，装备某型号导弹武器系统的我某部特点：人员满编率高，官兵军政素质过硬，长期驻守、训练在作战地域，对周围环境熟悉，驻地构筑了完备的发射要地、机动要道、隐藏工事、重要方向支撑点和指挥观察所，还配备了抗电磁干扰效能较好的大功率通信指挥设备。敌军的特点：作战经验丰富具有较强的综合作战能力，电子战、侦察探测和联合毁伤等能力突出，武器装备先进、技术水平较高，作战中干扰拦截我导弹武器系统的威胁较大。

4.1 计算可用度矩阵A

假设某导弹武器系统(含导弹子系统和火控子系统)对某一目标进行攻击，系统各平台平均无故障时间和平均修复时间如表1所示。

表1 各平台的平均无故障工作和平均故障修复时间

根据表1给出的数据和式(7)可知，导弹子系统和发射平台的可用性分别为

aM=0.976，aS=0.952.

由于侦察平台和操控平台均为并联工作，其可用性由公式(6)，(7)求取，即

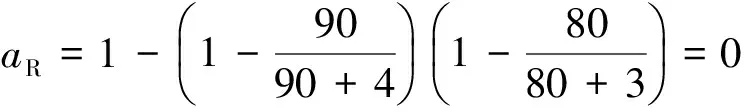
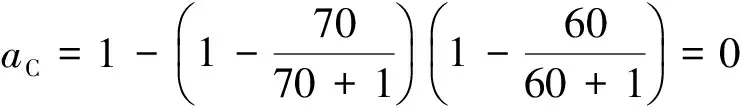
由式(5)可知，火控子系统正常运行的概率为

aH=aRaCaS=0.949.

再由式(4)可知，导弹武器系统的可用性矩阵为

A=(0.926， 0.023， 0.050， 0.001).

4.2 计算可信度矩阵D

假设在主动段，导弹子系统中其发动机的故障概率为Pf=0.04，而火控子系统的故障概率为Pg=0.07；导弹在中间段飞行过程中，其被拦截概率为Pt=0.25，火控子系统的遭到敌方破坏的概率为Ph=0.18；导弹在末段被拦截概率为Pj=0.35。

则由公式(8～11)可得到导弹在3个阶段的可信性矩阵，分别如下：

故系统的可信度矩阵为

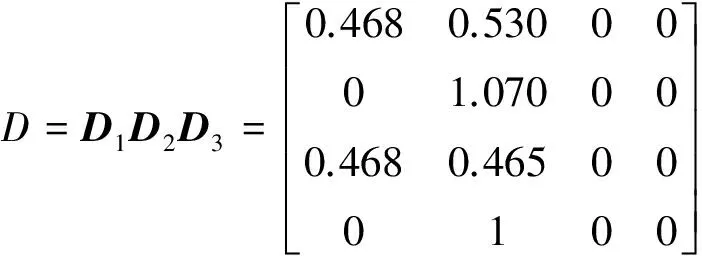
4.3 计算能力矩阵C

通过专家打分，用层次分析法构造判断矩阵并进行一致性检验，如表2所示，判断矩阵中的各元素数据来自导弹领域专家调查数据的统计分析，且满足T.L.Saaty提出的1～9标度。

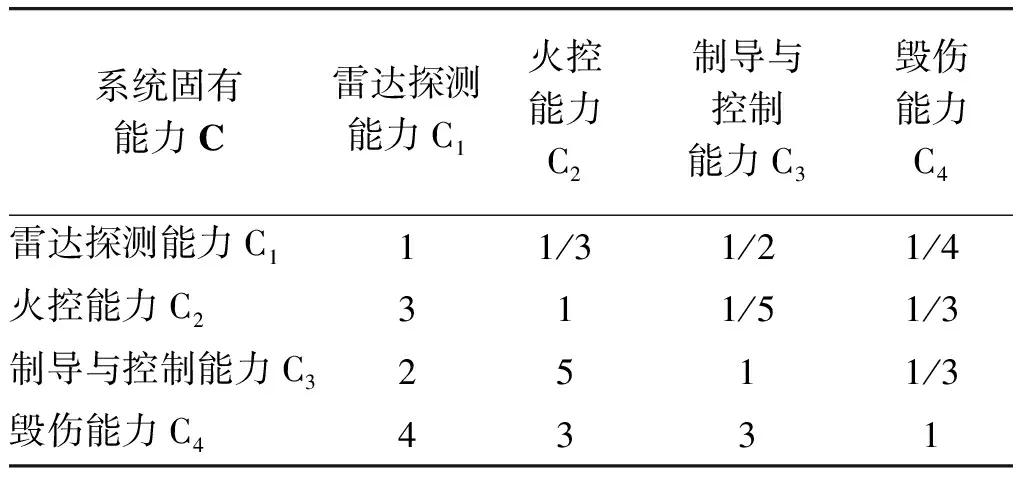
表2 系统固有能力子指标打分表

计算得：W=(0.089 6, 0.139 2, 0.295 6, 0.475 6)，λmax=4.495 6，C.I.=0.036 8，C.R.=0.040 1<0.1，故判断矩阵有满意的一致性指标。

求出导弹武器系统能力指标各层指标权重如表3所示。利用模糊关系合成原理计算能力值，搜索能力第3层经过计算有：

B11=(0.452 6，0.316 3，0.231 1)∘

(0.086 2, 0.037 6, 0.085 6, 0.109 9, 0.151 7, 0.082 6, 0.108 8, 0.086 7, 0.132 4, 0.077 9, 0.081 3).

同理，跟踪能力第3层经过计算有

B13=(0.156 1，0.230 4，0.214 2，0.101 5，0.297 8)∘

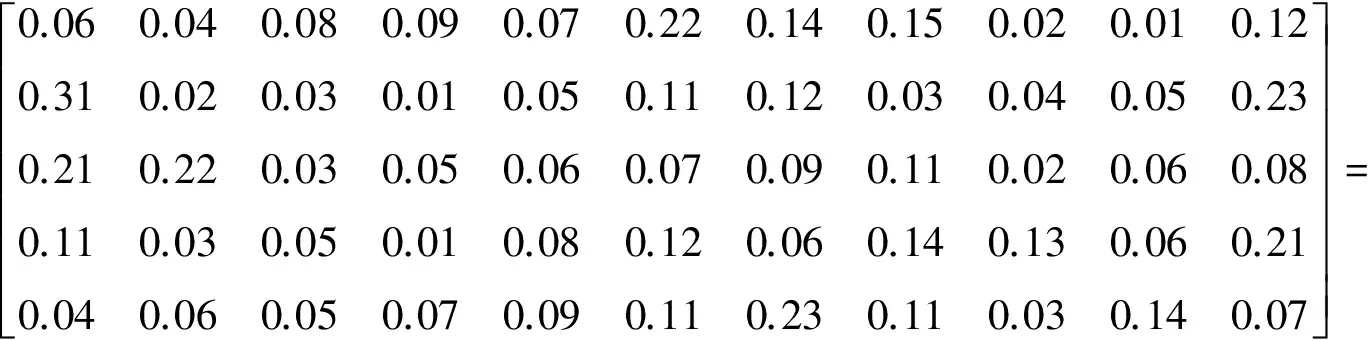
(0.148 8, 0.078 9, 0.045 8, 0.048 9, 0.070 2, 0.119 6, 0.143 4, 0.100 9, 0.038 8, 0.073 7, 0.131 0).

故

(0.105 0, 0.077 6, 0.097 8, 0.064 3,

0.082 4, 0.088 6, 0.112 3, 0.098 4,

0.076 7, 0.076 6, 0.133 6).

同理可得

B2= (0.095 4, 0.062 5, 0.058 8, 0.065 6,

0.051 8, 0.079 4, 0.084 5, 0.079 3,

0.085 3, 0.114 8, 0.217 0),

B3= (0.051 7, 0.055 5, 0.045 5, 0.081 3,

0.077 0, 0.099 8, 0.144 7, 0.105 8,

0.123 8, 0.110 9, 0.183 0)，

B4= (0.045 6, 0.060 0, 0.076 2, 0.130 9,

0.122 5, 0.051 1, 0.054 4, 0.100 9,

0.117 8, 0.110 5, 0.139 2).

B=(0.089 6, 0.139 2, 0.295 6, 0.475 6)∘

0.095 6, 0.072 8, 0.090 4, 0.099 1, 0.111 4,

0.108 2, 0.162 5).

故导弹武器系统正常工作时的能力值为

c1=B·VT=0.059 6×1+0.060 6×0.9+

0.066 7×0.8+0.101 2×0.7+0.095 6×0.6+

0.072 8×0.5+0.090 4×0.4+0.099 1×0.3+

0.111 4×0.2+0.108 2×0.1+0.162 5×0=

0.431 1.

则由式(13)可知，能力矩阵为

C= (c1，c1，0，0)T=

(0.431 1, 0.431 1, 0, 0)T.

4.4 计算操作人员能力素质系数K和战场对抗环境影响参数Q

结合实际情况和导弹武器系统的装备设计性能，得到操作人员水平系数K和战场对抗环境系数Q的各层权重值及相关参数表，如表4所示。

利用式(14)，(15)可知：

Q=0.275 7.

4.5 计算导弹武器系统综合效能E

由公式(2)可知：

E=KA(D1D2D3)C(1-Q)=0.845 0·

由此可知，在真实战场环境中，导弹武器系统的综合效能受敌方火力拦截、电子干扰、侦察探测和战场电磁环境影响较大，受自然环境影响相对较小，同时操作人员能力素质和满编率对系统效能的发挥也有较大影响，部队应保持一定的战备状态、人员满编率和军事训练强度，并注重思想政治教育、和开展心理疏导，加大对所属人员心理素质的训练。

5 结束语

本文从导弹武器系统发射使用过程中分阶段的特点出发，将传统ADC法中的系统可信性D分解为不同阶段下导弹可信性的乘积，并紧贴实战对抗背景，在效能评估中综合考虑了人员操作水平系数K和环境对抗系数Q的影响，得出的结论更符合为了作战中导弹系统的工作规律。与此同时，通过采用层次分析法、模糊综合评判法对ADC模型固有能力矩阵进行了定性分析和定量计算，有利于了解掌握不同因素对导弹武器系统整体效能的影响程度，为设计研发和实际作战使用提供了参考依据，该效能评估方法还同样适用于工作过程存在阶段性划分的其他系统。

[1] 牛坤,庞志兵.基于多目标决策理论武器装备效能综合评估方法[J].情报指挥控制与仿真技术,2005,27(1):50-53. NIU Kun, PANG Zhi-bing. A Comprehensive Method for Effectiveness Evaluation of Weapon System[J]. Information Command Control System & Simulation Technology, 2005,27(1): 50-53.

[2] 陈健,滕克难,杨春周.基于ADC法的反卫装备体系打击效能评估模型研究[J].舰船电子工程,2014,34(3):116-119. CHEN Jian, TENG Ke-nan, YANG Chun-zhou. Effectiveness Evaluation Model of Antisatellite Equipment SoS Based on ADC Method[J].Ship Electronic Engineering, 2014,34(3):116-119.

[3] 王君,赵杰,邵雷,等.基于ADC法的地空导弹武器系统效能评估模型[J].现代防御技术,2015, 43(6):13-20. WANG Jun, ZHAO Jie, SHAO Lei, et al. System Effectiveness Evaluation Model of Ground to Air Missile Based on ADC Method[J]. Modern Defence Technology, 2015, 43(6):13-20.

[4] 齐善明,李磊.基于改进ADC模型的指挥信息系统作战效能评估[J].舰船电子工程,2012,32(5):30-33. QI Shan-ming, LI Lei. Operational Effectiveness Evaluation of Command Information System Based on the Improved ADC Model[J]. Ship Electronic Engineering, 2012, 32(5):30-33.

[5] 金鑫,徐军,曾杰. 系统效能评估模型探索[J].指挥信息系统与技术, 2011,2(1):36-40. JIN Xin, XU Jun, ZENG Jie. The Research of System Effectiveness Evaluation Model[J]. Command Information System and Technology, 2011, 2(1):36-40.

[6] 徐征捷,张友鹏,苏宏升.基于云模型的模糊综合评判法在风险评估中的应用[J].安全与环境学报,2014,14(2):69-72. XU Zheng-jie, ZHANG You-peng, SU Hong-sheng. Application of Risk Assessment on Fuzzy Comprehensive Evaluation Method Based on the Cloud Model[J]. Journal of Safety and Environment, 2014,14(2):69-72.

[7] 李晓明,李娜,董守贵,等. 空空导弹武器系统作战效能评估系统设计[J].电光与控制,2013,20(12):101-104. LI Xiao-ming, LI Na, DONG Shou-gui, et al. Design of an Operational Effectiveness Evaluation System for Air-to-Air Missile System[J]. Electronics Optics & Control, 2013, 20(12): 101-104.

[8] 刘芬良,罗权,李泽恩. 某型两栖装甲车作战效能评估模型[J].火力与指挥控制,2014,39(2):169-172. LIU Fen-liang, LUO Quan, LI Ze-en. Model of Operational Effectiveness Evaluation in Amphibious Armored Vehicle[J]. Fire Control & Command Control, 2014, 39(2):169-172.

[9] 张乐,刘忠,张建强,等. 基于自编码神经网络的装备体系评估指标约简方法[J].中南大学学报:自然科学版,2013,44(10):4130-4137. ZHANG Le, LIU Zhong, ZHANG Jian-qiang, et al. Reduction Method of Weapon System-of-Systems Assessment Index System Based on Auto-Encoder[J]. Journal of Central South University: Nature Science ed, 2013, 44(10):4130- 4137.

[10] 顾鸿,赵晓东,陈红江. 舰艇编队对抗效能评估[J].兵工自动化,2014,10(3):7-10. GU Hong, ZHAO Xiao-dong, CHEN Hong-jiang. Combat Effectiveness Evaluation for Warship Formation[J]. Ordnance Industry Automation, 2014, 10(3):7-10.

[11] 齐玲辉,张安,郭凤娟,等. 战术弹道导弹系统效能评估SEA法的建模与仿真[J].系统仿真学报, 2013, 25(4):795-799. QI Ling-hui, ZHANG An, GUO Feng-juan, et al. Modeling and Simulation of SEA Method for Effectiveness Analysis of Tactical Ballistic Missile System[J]. Journal of System Simulation, 2013, 25(4):795-799.

[12] 董尤心. 效能评估方法研究[M].北京:国防工业出版社,2009:27-29. DONG You-xin. Research on the Method of Effectiveness Evaluation[M].Beijing: National Defence Industry Press, 2009: 27- 29.

[13] 赵纪华,吴勇. 基于模糊层次分析法的装备性能评估[J].四川兵工学报,2010,31(11): 53- 55. ZHAO Ji-hua, WU Yong. Assessment of Effectiveness for an Equipment Based on Fuzzy Arrangement Analysis Method[J]. Journal of Sichuan Ordnance, 2010, 31(11):53- 55.

[14] 周燕,陈烺中,李为民. 基于BP神经网络的弹炮结合系统作战效能评估[J].系统工程与电子技术,2005,27(1):84-86. ZHOU Yan, CHEN Lang-zhong, LI Wei-min. Assessment of Operational Effectiveness for the Bullet-Shell System Based on the BP Network[J]. System Engineering and Electronics, 2005, 27 (1):84-86.

[15] 李德毅,杜鹢. 不确定性人工智能[M].北京:国防工业出版社,2005. LI De-yi, DU Yi. Artificial Intelligence with Uncertainty[M]. Beijing: National Defence Industry Press, 2005.

Effectiveness Evaluation of Missile Weapon System Based on ADC Improved Model

XIA Wei, LIU Xin-xue, MENG Shao-fei, FAN Jin-long

(Rocket Force University of Engineering, Shaanxi Xi’an 710025, China)

In order to improve the whole effectiveness evaluation of the missile weapon system with stage characteristics of flight course, break missile weapon system reliability (D) into product of initiative stage, middle stage and reentry stage, put forwards the ADC system effectiveness evaluation method by stage. Considering the point of battlefield confrontation, this paper improves the ADC model by using coefficient of operators' level of missile weapon system (K) and battlefield confrontation coefficient (Q). The effectiveness evaluation index system of missile weapon system is brought forward and a new improved effectiveness evaluation model (ADC improved model) is proposed. At the same time, according to the construction mechanism and operation of campaign, the missile operational effectiveness is quantized by using experts mark, arrangement analysis, fuzzy comprehensive evaluation and weighted summation method. By case analysis, it is proved that this proposed method is of correctness and availability, which brings about the scientific decision-marking basis for the design and application of missile weapon system.

missile weapon system; effectiveness evaluation; ADC improved model; stage characteristics; fuzzy comprehensive evaluation; analytic hierarchy process (AHP)

2016-04-26；

2016-07-10 作者简介：夏维(1982-)，男，重庆长寿人。博士生，研究方向为军事运筹学。

10.3969/j.issn.1009-086x.2017.02.005

TJ760.6;O159;TP301.6

A

1009-086X(2017)-02-0030-010

通信地址：710025 陕西省西安市灞桥区洪庆镇同心路2号2906分队 E-mail：xiawei66@163.com