轴对称研究与解题中的应用

江苏省扬州市广陵区头桥中学(225109)

黄 慧●



轴对称研究与解题中的应用

江苏省扬州市广陵区头桥中学(225109)

黄 慧●

本文从提高读者应用轴对称思想出发，首先研究轴对称的基础知识要点，轴对称图形特点，对称轴，对称点，对称图形关于对称轴的关系，本文又提供轴对称必要掌握的基本技能，本文第三部分举实例说明对称思想在解题中的应用.

对称轴；对称图形；对称点；最值问题

一、基础知识要点

轴对称图形:将一个图形沿着某一条直线翻折，如果直线两旁的部分能够重合，那么这样的图形叫做轴对称图形.

两个图形关于某条直线对称:平面上的两个图形，将其中一个图形沿着某一条直线翻折过去，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称.这条直线就是对称轴.

对称点:两个关于某条直线对称的图形中的对应点(即两图形重合时互相重合的点)叫做关于这条直线的对称点.

两个图形关于某条直线对称的性质:如果两个图形关于某一条直线对称，那么连接对应点的线段被对称轴重直平分.

如果连接两个点的线段被一条直线垂直平分，那么这两点关于这条直线对称.

二、基本技能

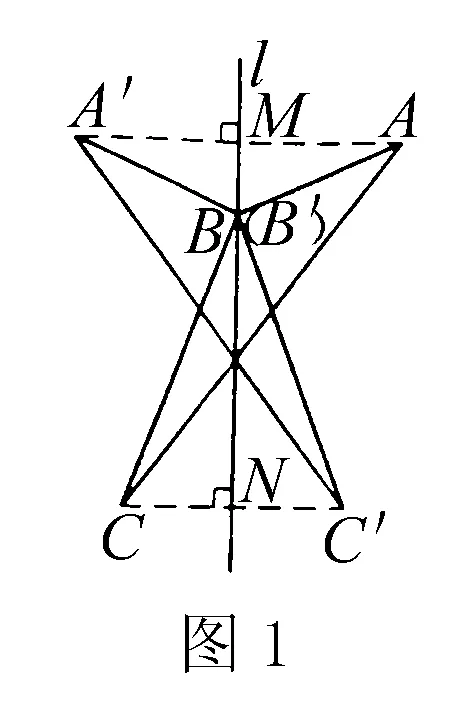
例1 如图1，已知△ABC和直线l，画出△ABC关于直线l对称的△A′B′C′.

分析 要画出△ABC关于直线l对称的△A′B′C′，只要分别画出点A、B、C关于直线l的对称点A′、B′、C′.根据两个图形关于某一直线对称的性质(如果连接两个点的线段被L直线垂直平分，那么这两点关于这条直线对称)，就可以画出点A、B、C关于直线l的对称点了.

(1)分别过点A、C画直线l的垂线，垂足分别为M、N.再延长AM、CN到A′、C′，使得A′M=AM，C′N=CN.

(2)因为点B在直线l上，所以点B关于直线l的对称点B′和B重合.

(3)顺次连接A′B′、B′C′、A′C′，得△A′B′C′,就是所要画的三角形.

说明 画对称图形的实质是画对称点.画一点关于直线对称的点，可从这点向直线画垂线，得一条垂线段，再延长后取相等的线段即得到要画的对称点.如果这点在直线上，那么它关于这条直线对称的点就是它本身.

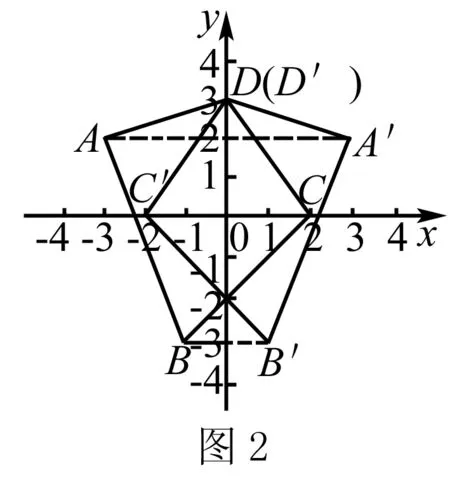
例2 如图2，在直角坐标平面内，四边形ABCD的顶点A、B、C、D的坐标分别为(-3，2)、(-1，-3)、(2，0)、(0，3)，画出四边形ABCD关于y轴对称的四边形A′B′C′D′，并写出点A′、B′、C′、D′的坐标.

分析 画四边形ABCD关于y轴的对称图形四边形A′B′C′D′，只要画出点A、B、C、D关于y轴的对称点A′、B′、C′、D′.

分别画出点A、B、C、D关于y轴的对称点A′、B′、C′、D′，它们的坐标分别为(3，2)、(1，-3)、(-2，0)、(0，3)；顺次连接A′B′、B′C′、C′D′、D′A′，则四边形A′B′C′D′就是所画的对称图形.

说明 一般地说，直角坐标平面内一点P(x,y)，它关于x轴对称的点为P1(x,-y);关于y轴对称的点为P2(-x,y).

三、对称思想在应用

近年来的中考试题中，最值问题成为设计压轴题的一种常见设问，它主要与函数知识进行综合，如以抛物线为背景的最值问题在中考中就十分抢眼.解决此类问题时，主要通过作对称的方法，作出取得最小值时的点，然后结合几何、函数等知识进行最值求解.下面结合几例考题，与大家研究.

例3 如图3，已知抛物线y=ax2+bx+1经过点A(1，3)和点B(2，1).

(1)求此抛物线解析式；

(2)点C、D分别是x轴和y轴上的动点，求四边形ABCD周长的最小值；

解析 (1)易得抛物线的解析式为y=-2x2+4x+1.

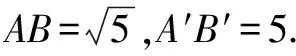
评注 一般地，解决此类问题主要是利用“两点之间线段最短”和“任意两边之和大于第三边”，因此只要作出点A(或点B)关于直线的对称点A(或B)，再连接BA1(或AB1)即可.

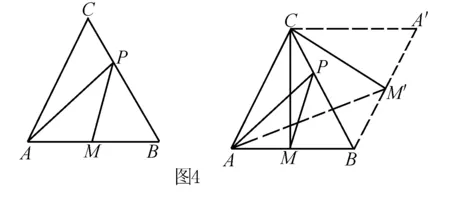
例4 设正三角形的边长为2,M是AB边上的中点,P是边BC上的任意一点,PA+PM的最大值和最小值分别为记为s和t,则s2-t2=____.

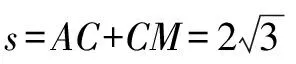
G632

B

1008-0333(2017)11-0006-01