清水河上游张家口站汛前枯季来水量预测模型

姜璞玉

摘要 利用清水河上游张家口水文站多年汛前枯季实测径流和流域面平均雨量系列资料，分析了二者之间存在的内在关系，得出了相关模型和有关参数，从而为清水河橡胶坝群调蓄和水利工程建设提供理论依据和参考资料。

关键词 枯季径流；变化规律；预测模型；清水河上游；河北张家口

中图分类号 P333.3 文献标识码 A 文章编号 1007-5739（2017）06-0218-02

河川枯季径流主要有枯季降水量和流域内蓄水补给，流量过程一般呈较稳定的消退规律。影响消退规律的因素包括蓄水量、地面及表层滞水情况、土壤入渗能力、岩层渗水性、流域比降、湖泊度、植被等。另外，枯水期的天气、气候变化、用水、耗水情况也影响枯季径流及其过程[1-3]。

本文通过对清水河张家口水文站以上区域枯季降水径流的时空分布规律进行探讨，研究流域枯季径流特性规律；利用位于清水河中下游的张家口水文站及上游雨量站1986—2015年实测水文资料，并试用2种方法建立汛前枯季来水量模型。其成果为流域水资源管理、保护、开发利用、枯季水量调度等工作提供一定的技术支撑。

1 流域概况

清水河是永定河水系洋河干流上的主要河流。发源于崇礼县桦皮岭一带，上游在崇礼县分成东沟、正沟、西沟3支，汇合后贯穿张家口市区汇入洋河，流域面积2 830 km2，全长122 km，市区段23.5 km。流域全境山峦起伏、沟壑纵横，海拔在800～1 000 m之间，地表植被情况差异较大。清水河经过4期综合治理，现已建成蓄水橡胶坝31座，蓄水长度23.5 km，蓄水量533万m3。1986—2015年多年平均实测流量为1.10 m3/s，多年10—12月平均实测流量为0.82 m3/s，多年1—5月平均实测流量为0.45 m3/s。

2 枯季径流变化规律分析

2.1 枯季径流年际变化

选取张家口水文站及上游流域1986—2015年降水、流量资料，绘制年降水量过程线和年平均流量及枯季平均流量过程线，见图1、2。可以看出，径流量年际变化比降水量大，主要原因是受下垫面变化影响[4-5]。

2.2 枯季径流年内分配规律

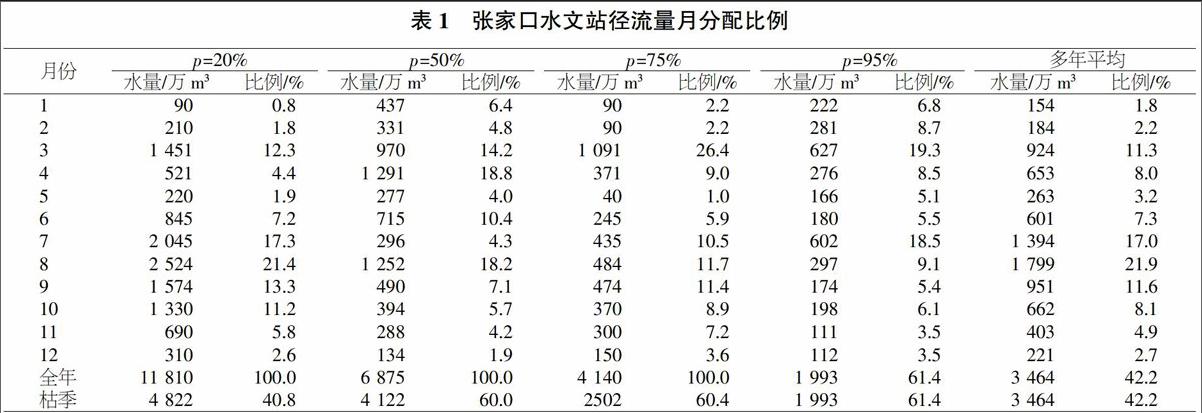
由于存在下垫面因素的作用，导致径流年内分配和降水年内变化规律有较大的相似之处，又存在明显的不同[6-7]。其中，多年平均枯季径流量在全年径流量中占有较大的比率，达到42.2%。

通过分析张家口水文站年径流量月分配数据可知，径流量年内分配存在一定的规律，即径流量年内分配中1—2月的径流量比率最低；到3月时，由于春季气温上升，水体解冻而发生凌汛，使3月的径流量比率增加；到4—5月时，由于凌汛已过，径流量所占比率又减少；进入夏季以后，张家口地区进入雨季，因为降雨增加，所以6—8月径流量所占比率又开始增加，特别是进入7月和8月，径流量达到最大；进入秋季以后，随着雨季的结束，9—12月径流量所占比率也逐渐减少，次年1月的径流量所占比率达到谷底。张家口水文站年径流量月分配比例见表1。

3 枯季来水量模型预测

3.1 前后期径流量相关模型

3.1.1 模型建立。由于当年10月与次年5月出现洪水，往往使实测径流增加，故剔除相关数据。然后，对张家口水文站1986—2015年的10—12月和次年1—5月实测径流数据资料进行线性回归分析，一元直线回归方程如下：

W次年1-5=a+b×W当年10-12（1）

式（1）中，a为流域基流量（剔除10—12月径流影响）；b为体现下垫面条件影响的斜率系数，其受到地质、地貌及植被等多种因素综合影响。a、b均为待定系数。

将对张家口站1986—2015年30年系列数据（当年10—12月和次年1—5月）进行相关模型分析，得出a=207.7，b=0.525，相关系数R2=0.839。所得模型具体见图3。

3.1.2 模型演算及误差分析。利用拟合的验算公式进行演算，求得平均相对误差为1.8%，最大相对误差为28.1%。若考虑冰情等因素的影响，可以进一步减少相对误差，提高预测精度。如果预见期内有较大降雨量，则需考虑降雨的影响，可以将预见期内降雨作为参考建立相关图。

3.2 前期降水量与径流深相关模型

3.2.1 模型的建立。在流域的水文地质条件和河流特性已确定的情况下，前期有效降水是影响枯季径流的决定性因素。前期有效降水越充沛，渗入地下的水量就越多，枯季河川基流量就越大。

利用张家口站1986—2015年流域面雨量与1—4月实测径流深资料，以前期降水对流域枯季径流影响为依据，进行前期降水与枯季径流相关模型演算分析，得出一元线性回归方程如下：

R′1-4=a+b×Pi（2）

式（2）中，Pi为前期降水，R′1-4为预测的1—4月径流深，a（前期无效降水）、b（斜率）均为未待定系数，与流域的地质、地貌及植被等下垫面条件密切相关。

由此得出以下流域面雨量计算公式：

Pi=P1×α+P2×β（3）

式（3）中，P1、P2分别表示上一年和前一年的流域面雨量，α、β分别表示上一年和前一年雨量对径流影响的权重。

经调试适线，求得α=0.62、β=0.38时所拟合的相关线为最优。此时，a=-79.58，b=0.240，相关系数R2=0.830。张家口站1986—2015年前期降水与1—4月实测径流深相关模型见图4。

3.2.2 模型演算及误差分析。利用所拟合的一元直线回归方程进行模型演算。模型拟合值R1-4加上1986—2015年5月实测径流深均值R5=0.3 mm，即为汛前枯季径流深模型预测值。经模型演算，求得1—4月实测径流深平均相对误差为2.7%，最大相对误差为29.4%，可满足预测精度的要求。预报时降雨参数为未知量，需由长期天气预报提供，其误差必然直接影响径流预报精度。

4 结语

通过分析张家口水文站1986—2015年30年中的10—12月和次年1—5月实测径流资料获得的模型，可以对汛前枯季来水量进行预测。该模型平均相对误差为1.8%，最大相对误差为28.1%，可以达到实践中对汛前枯季来水量预测的要求，模型简单实用。

同時，利用张家口站1986—2015年流域前期降水量与1—4月实测径流深资料建立的预测模型，可以对张家口站汛前枯季来水量进行预测。该模型实测径流深平均相对误差为2.7%，最大相对误差为29.4%，可以满足预测精度的要求。

枯季径流区域预测模型的建立能够有效地解决区域内河流的枯季预报问题。由于枯季径流量较小，各种影响因素的变化易使枯季流量发生波动。因此，上述2种预测模型在实际应用中应当考虑冰情、人类活动等因素的影响，识别主要影响因素和次要影响因素，以提高预测方案的精度和可靠性。

5 参考文献

[1] 包为民.水文预报[M].4版.北京：中国水利水电出版社，2009.

[2] 陶凤玲，刘海波，王思茹，等.基于降水-径流模型的中长期径流预测[J].水利水电技术，2012（1）：27-29.

[3] 宋亚娅，朱妙艺，朱富军，等.降雨径流模型及其应用[J].水电能源科学，2012（6）：9-12.

[4] 陈会丽，杨小柳.一个三参数的降雨径流模型及其在我国的应用[J].水文，2015（2）：17-21.

[5] 王瑾杰，丁建丽，张成.普适降雨-径流模型SCS-CN的研究进展[J].中国农村水利水电，2015（11）：43-47.

[6] 刘根生.黄河河源区枯季径流模型的研究及应用[J].甘肃水利水电技术，2003（4）：278-280.

[7] 李洪加，王利国.降雨径流模型在年径流还原计算中的应用[J].黑龙江水利科技，2003（3）：118.