基于模糊PID双模控制Buck电路的仿真研究

刘洪霞，闫兴德

（1.安徽科技学院，安徽凤阳233100；2.蚌埠供电公司，安徽蚌埠233010）

基于模糊PID双模控制Buck电路的仿真研究

刘洪霞1，闫兴德2

（1.安徽科技学院，安徽凤阳233100；2.蚌埠供电公司，安徽蚌埠233010）

针对传统PID控制方法在对Buck电路进行控制时精度低、抗干扰能力差等缺点，提出了一种基于模糊PID双模控制的闭环调节系统。采用数学工具Matlab为仿真软件，通过传统PID以及模糊PID两种方法调节Buck电路脉宽来实现调压。首先介绍了buck电路，对buck电路进行了传统PID闭环控制的仿真；然后进行了模糊PID双模控制器的系统设计和仿真；最后对传统PID控制和模糊PID双模控制的仿真结果进行了比较，得出结果：模糊PID双模控制算法使Buck电路具有更好的抗干扰能力和精度。

Buck电路；Matlab；PWM；模糊PID

BUCK电路是直流斩波电路应用最为广泛的一种电路形式。广泛应用于开关电源、稳压器及其他电压变换电路中，对其控制策略进行研究有着重要的意义。在BUCK电路中，通过调节其开关元件VT的脉宽可以实现对输出电压的控制。从输出电压引入负反馈，使用传统PID、模糊PID两种控制方法对其开关元件的脉宽进行调制，来实现输出电压的闭环可控及提高输出电压精度。

1 Buck电路

Buck电路又称Buck Chopper，将一种直流电路斩波成另外一种直流电路，但是由于输出电压只能低于输入电压，所以又称为降压式变换电路[1]。其电路原理如图1所示。

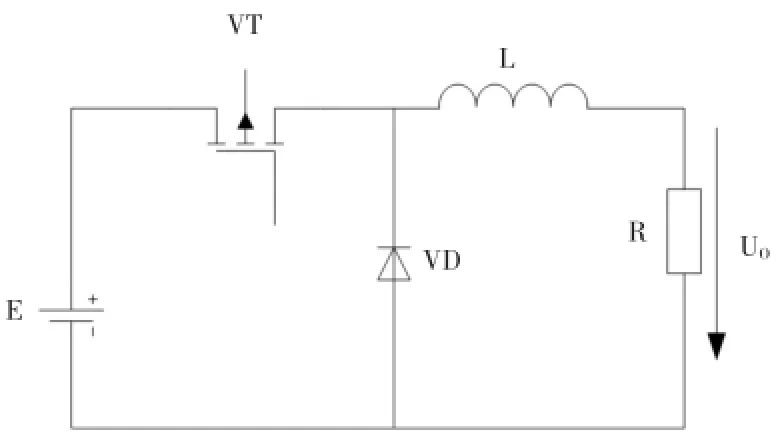
图1Bcuk电路

电路中使用一个全控型器件VT可以是MOSFET也可以是IGBT。假设在t=0时刻，驱动VT导通，E向负载供电，输出电压Uo=E，当t=t1时刻VT关断时，有电感L向负载续流供电，当电感L较大时有[2]：

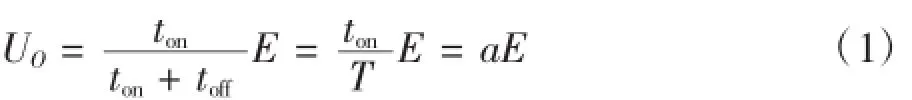
式（1）中α为占空比，可以通过控制开关器件的占空比来控制输出电压的大小，以此实现降压的目的。

2 基于PID控制的闭环调节系统

通过从输出端引回的电压值与设定值进行比较，根据比较值生成PWM脉宽。由于引入的负反馈，输出端电压值大于设定值时，脉宽就会减小，也就是式（1）中的占空比α减小，从而使输出电压减小；反之同理，当输出的电压值小于设定值时，脉宽增大，输出电压增大，最终使输出值与设定值相等，电路稳定。PWM波生成的原理如图2所示。

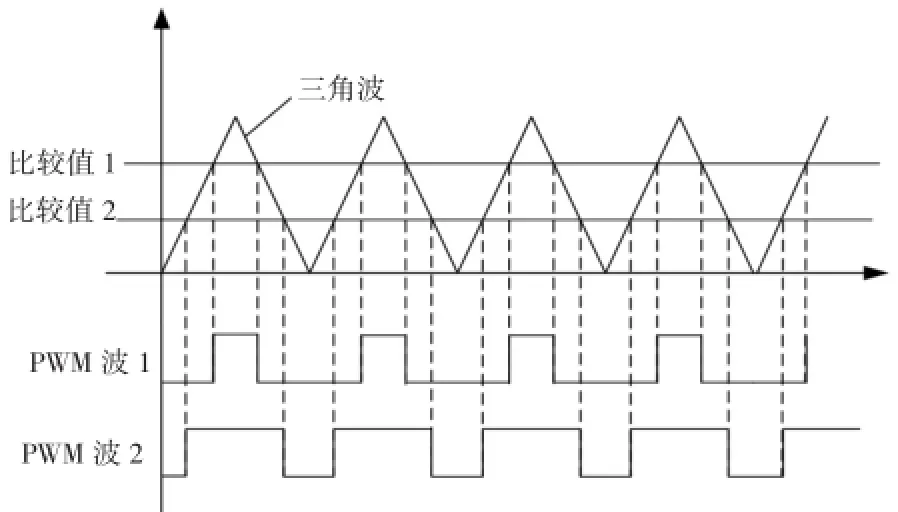
图2PWM生成原理图

比较值的设定是根据差值调节的，差值（设定值-输出值）大时，比较值会下调增加PWM脉宽[3]。为了使脉宽占空比与电压值对应，输出误差值需要乘以一定比例因子才能成为控制量。当只采用比例因子时，可以加快系统响应速度，但是往往是由于有余差的存在使输出结果不能稳定在一个理想的输出值，有可能出现较大超调量，使系统扰动、震荡，甚至导致稳定性的崩溃。积分环节是对误差取积分，随着时间的增加，积分项会增大，这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。微分项具有超前作用，适用于有较大惯性或滞后的被控对象，如温度控制、水量控制等。当引入的微分项设置得当时，能有效提高系统的动态性能指标，减小系统超调量及动态误差，增加稳定性[4]。基于PID控制的闭环调节系统仿真模型如图3所示。

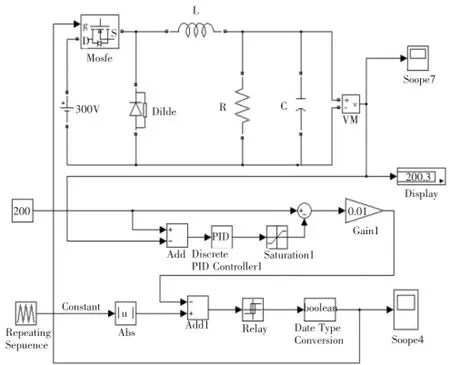
图3PID控制闭环调节系统仿真模型

本文使用的Buck电路输出端含有滤波电容，为保证输出的连续的连续需要电感L满足下面公式[5]。

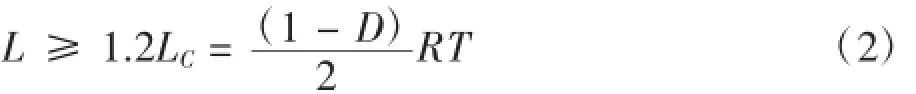
滤波电容为

其中，LC为保证输出连续的临界电感，ΔUO为纹波电压，D为占空比。PWM波生成器采用的为图2原理，三角波与比较值比较过后经过布尔运算转化为方波脉冲信号给全控型器件来影响输出值，给定值与输出值比较经过PID运算及比例因子生成比较值，从而形成闭环控制电路[6]。本文中的全控型器件选用MOSFET，直流电压最大值设定为300 V，三角波幅值最大为3，比例因子为0.01，这样在最大占空为1时比对应输出最大电压300 V.

PID控制闭环调节系统仿真结果如图4所示，由于引入反馈环节，系统可以根据设定值自动调节输出电压，直至系统输出电压达到设定值后趋于平稳，并且由于二级管等开关器件而引起的误差信号也会消除，由于开关开通瞬间形成的脉冲得到了一定的遏制，系统的鲁棒性得到了提高[7]。

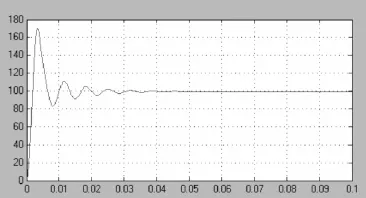
图4 传统PID控制闭环调节系统仿真结果

PID控制中的kp、ki、kd三个参数需要有一个最合理的搭配，输出效果才能理想，但是PID参数的调试较为繁琐，要根据个人经验及试验结果多次拼凑[8]。

3 基于模糊PID双模控制的闭环调节系统

本文引用模糊PID双模控制方法，由于系统运行前期幅值偏离比较大，采用PID调控受步长限制，难以短时达到效果，对前期暂态控制误差不理想。模糊PID双模控制方法，根据误差变化量的大小进行调控，前期误差较大时，选择模糊控制，采用较大的步长及时限制误差，误差达到指定值后转而PID控制[9]，能够满足系统有较小的稳态误差，其控制策略如图5所示。

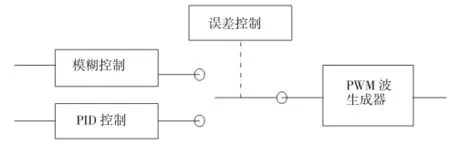
图5 控制策略图

以输入误差为控制选择开关，当误差较大时选择模糊控制方案，以此来提高调解幅度，当误差较小时选择PID控制方案，来提高稳态精度。其Matlab仿真模型为图6所示。相比PID控制，双模控制多出一个模糊控制器和一个选择开关。模型中选择开关设定值为50，当误差e＞50时采用模糊控制大幅度调解调控量，e≤50时采用PID控制提高输出精度。

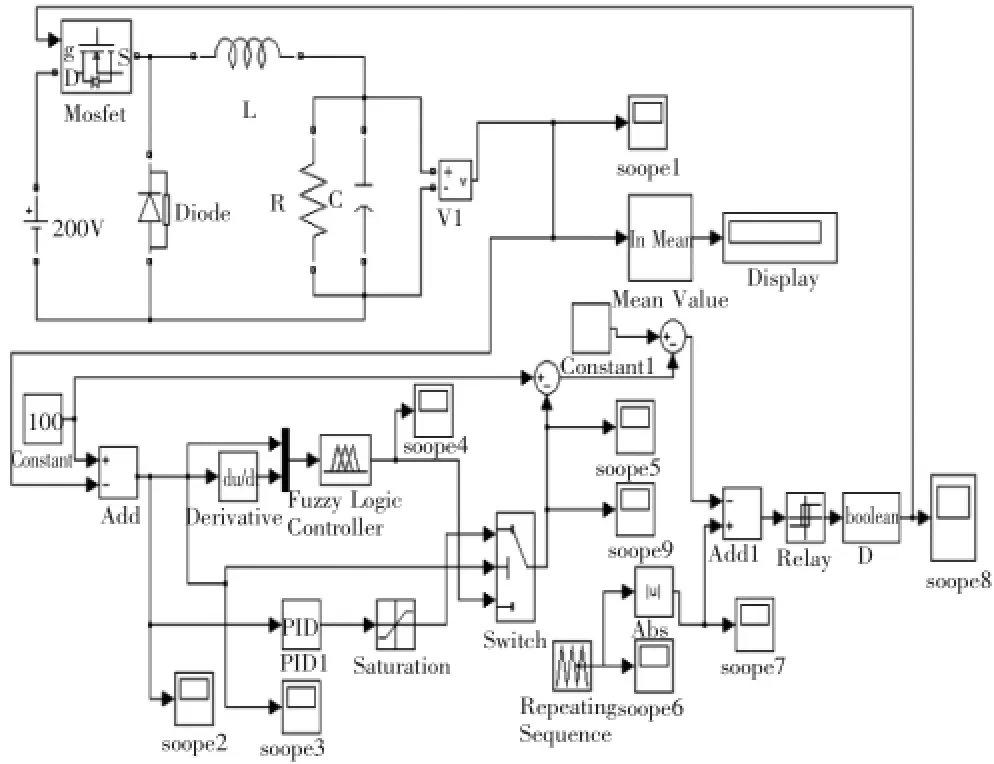
图6 模糊PID双模控制仿真模型

4 实验验证

模糊PID双模控制方案如图7所示，四个方块分别为模糊编辑器、模糊规则推理器、模糊规则浏览器、输入输出曲线图中的相关设置[10]。仿真时设置最大步长为1e-6，允许误差为1e-6，仿真时间为0.1 s.

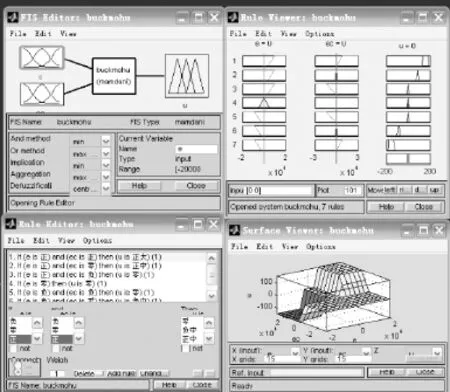
图7 模糊PID双模控制方案图

仿真结果如图8所示。

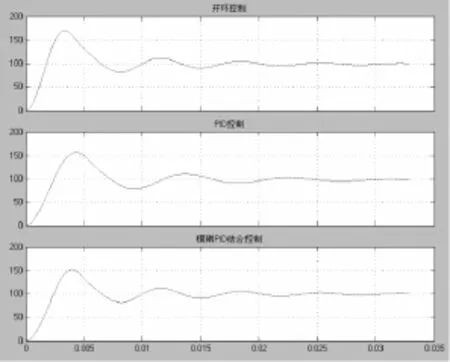
图8 模糊PID双模控制仿真结果

由图8和图4比较分析可知：传统PID闭环控制中前期暂态浮动较大，模糊PID双模控制中暂态值得到了一定遏制，调整时间也变短，模糊PID双模控制较传统PID控制效果好。

5 结束语

模糊PID双模控制将模糊控制和PID控制两者结合在一起，既有模糊控制的灵活性和适应性强的优点，又具有PID控制精度高的特点，具有很好的抗干扰能力，提高了系统的可靠性和精度，有一定的应用价值。

[1]王兆安．电力电子技术[M].北京：机械工业出版社，2012.

[2]林飞，杜欣．电力应用技术的MATLAB仿真[M].北京：中国电力出版社，2009.

[3]何芝强.PID控制器参数整定方法及其应用研究[D].杭州：浙江大学，2005.

[4]李林航.基于DSP的模糊PID控制器的研究[D].成都：西华大学，2007.

[5]陶波，朱玉琴.改进的动态规划法在车辆最短路径问题中的应用[J].重庆工学院学报，2009，23（1）：24-27.

[6]陈以，万梅芳．RBF神经网络在物流系统中的应用[J]．计算机仿真，2010，27（4）：159-163.

[7]阳春华，谷丽姗，桂卫华.自适应变异的粒子群优化算法[J].计算机工程，2008，56（16）：188-190.

[8]苏高利,邓芳萍.论基于MATLAB语言的BP神经网络的改进算法[J].科技通报，2003，30（02）：102-105.

[9]温浩，赵国庆.基于MATLAB神经网络工具箱的线性神经网络实现[J].电子科技，2005，15（01）：51-54.

[10]廖政伟，张雪，尤伟，等.应用于超宽输入范围的变拓扑LLC电路[J].浙江大学学报（工学版），2013，47（12）：2073-2079.

Study and Simulation of Buck Circuit Based on Dual-mode control of Fuzzy-PID

LIU Hong-xia1，YAN Xing-de2
（1.Anhui University of Science and Technology，Fengyang Anhui 233100，China；2.Bengbu Power Supply Company，Bengbu Anhui 233010，China）

This paper presented a new method based on the Fuzzy-PID for Buck Circuit.This method overcomes some defects of the traditional PID control，such as lower control precision and worse anti－jamming performance．We use Matlab for the simulation，it is a mathematical tool.We adjust the PWM of Buck circuit by traditional PID and fuzzy PID to achieve the regulator.At first，the paper introduced the buck circuit,and implemented the simulation of traditional PID control，then implemented the simulation of traditional PID control Fuzzy－PID control.At last，it compared simulation results of PID control method with Fuzzy－PID control method.The results show that the Fuzzy－PID control method has more excellent dynamic and anti－jamming performance．

buck circuit；matlab；PWM；fuzzy PID

TP273

A

1672-545X（2017）03-0069-03

2016-12-01

安徽科技学院校级项目（编号：ZRC2014454）。

刘洪霞（1985-），女，山东临沂人，助教，硕士,主要从事电工电子技术方面的教学及研究工作。