H.264运动估计算法比较与分析

刘书平

（四川大学计算机学院，成都 610065）

H.264运动估计算法比较与分析

刘书平

（四川大学计算机学院，成都 610065）

针对H.264/AVC编码器中几种典型的运动估计算法进行研究，并用基本的测试视频序列对这几种运动估计算法进行实验和测试，实验结果表明优化的运动估计算法UMHexagonS和精简的UMHexagonS（SUMHexagonS）在保持PSNR基本不变的情况下大大减少运动估计时间和整体的编码时间，并且编码每帧使用的比特数基本不变。同时总结出运动估计算法的优化方向，为以后的优化工作奠定基础。

运动估计；FS；UMHexagonS；SUMHexagonS；PSNR

0 引言

运动估计算法是视频编解码算法的核心，优化运动估计算法可提高运动估计的速度，减少运动估计时间，从而大大减少编码时间，提高编码效率。通过对运动估计算法及其优化算法的研究，能够从前人优化的经验中找到优化方向，同时掌握优化最新进展，从而开发出新的更高效的运动估计算法。

H.264标准中，每一帧图像都被分成大小相同的宏块，即以宏块为基本处理单元。运动估计的基本思想为：首先，将帧中每个宏块分成多个互不重叠的块，并且假设每个分块内部所有像素的运动方向一致，然后对当前宏块中的每一块，在当前帧的前面帧的一帧或多帧中的某一给定搜索范围按照一定的匹配原则和搜索策略找出和当前块最为相似的块，也就是最佳匹配块，最后通过计算最佳匹配块和当前块的相对位置得到运动位移，该运动位移记为当前块的运动矢量（MV）。对匹配块和当前块的差值、运动矢量和相应的参考索引进行编码。运动估计研究的主要内容就是如何快速有效地找到最佳匹配块并计算出运动矢量。

1 常用的快匹配准则

均方误差（Mean Square Error，MSE）

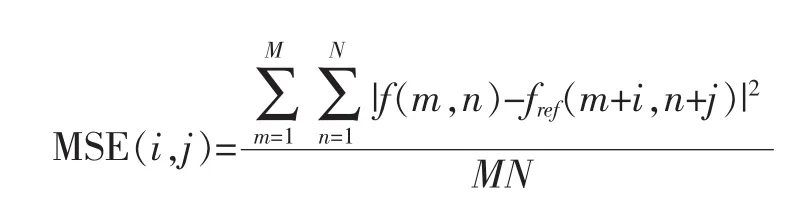
平均绝对误差 （Mean Absolute Difference/Error，MAD/MAE）

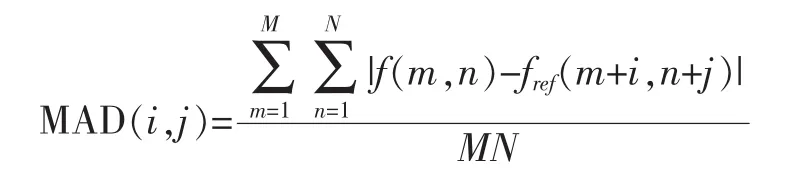
绝对误差之和 （Sum of Absolute Difference/Error，SAD/SAE）

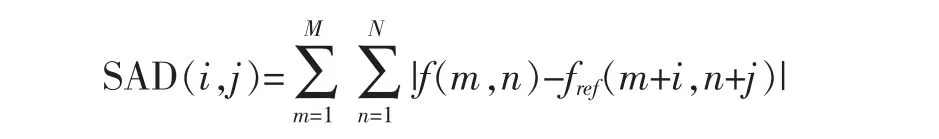
归一化互相关函数 （Normalized Cross-Correlation Function，NCCF）

其中，（i，j）为运动矢量，f和fref为当前帧和参考帧的像素值，M×N为宏块的大小，各匹配准则值最小时的（i，j）为最佳运动矢量，MSE精度最高，运算量最大，MAD和SAD精度相同，SAD运算量更小，只涉及减法和求绝对值的运算，一般选择SAD作为匹配准则。

2 几种典型的运动估计算法介绍

2.1 FS

FS（全搜索算法，Full Search）对搜索窗口中的所有像素点进行SAD值计算，并从得到的所有SAD中找出最小的SAD值，它对应的点所对应的偏移量即为所求的运动矢量，全搜索算法的搜索方式有2种：光栅式全搜索和螺旋式全搜索，下面以光栅式全搜索为例进行说明。如图1所示，光栅式搜索是从搜索窗口的左上角开始按照从左到右从上到下的顺序对搜索窗口中每一个像素点进行SAD值计算，直到搜索窗口中所有像素点的SAD值都被计算完为止，然后比较所有像素点的SAD值选出最小的SAD值，其对应的位移量即为运动矢量。通过全搜索算法找到的匹配点一定是全局最佳匹配点，然而它的计算量太大很难满足实时处理的要求，所以实际应用中很少采用。

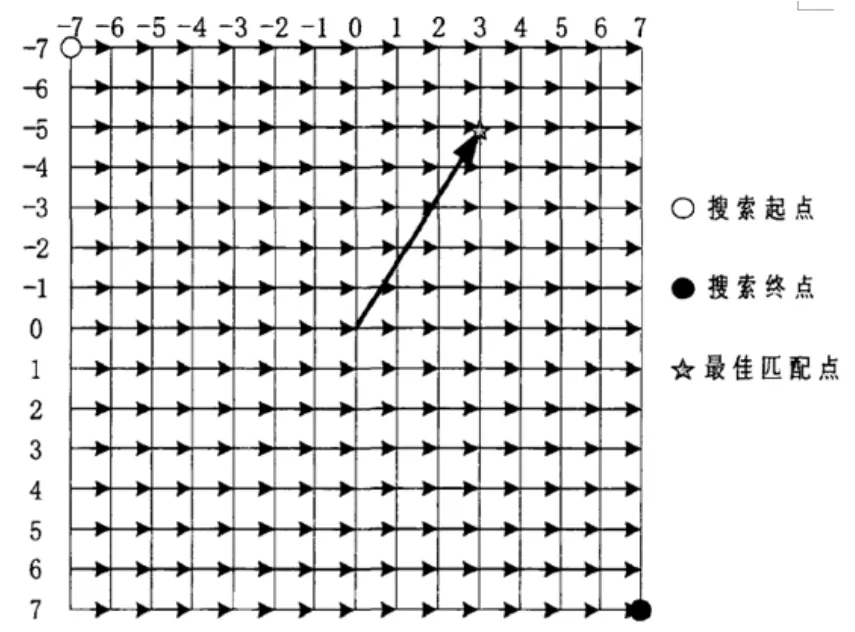
图1 光栅全搜索的过程图示

2.2 UMHexagonS

UMHexagonS算法[1]是由清华大学的Zhibo Chen等人提出来的一种快速运动估计算法，属于混合型搜索算法，之所以称之为混合型搜索算法是因为它分为4步，每一步都采用不同的搜索模式。

4个步骤分别为：搜索起始点预测，非对称十字形搜索，不均匀多层六边形搜索和扩展的六边形搜索。UMHexagonS在每一个搜索步骤之后都使用了提前终止判断函数，如果满足搜索终止条件则终止当前搜索步骤，直接进入后面的扩展的六边形搜索中的步骤，提前终止判断函数（EARLY_TERMINATION）使用提前检测零块的技术实现，所谓零块，即变换系数经量化后全为零的块，经过理论推导，得出如果搜索块的SAD（绝对误差之和）小于门限值Ti则搜索结束，而对于不同的块模式门限值Ti不同，当然，如果当前最小代价函数值比SAD（SAD小于门限值Ti的前提下）还小，则搜索过程也该停止，UMHexagonS还使用预测的SAD值来代替原始SAD值从而加快运动估计速度，门限值Ti的选择、SAD的预测及具体的理论推导参见文献[2]。

UMHexagonS步骤为：

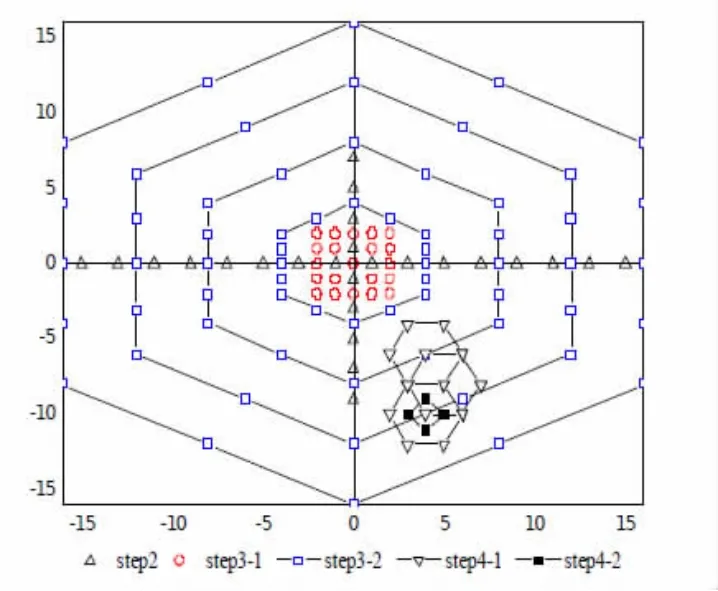
图2 UMHexagonS步骤实例（假设起始搜索点为（0，0），搜索窗口水平搜索范围W=16）

（1）搜索起始点预测

使用运动矢量预测方法（中值预测，上层预测，对应块预测，相邻参考帧预测）对当前块的运动矢量进行预测，选取代价最小的运动矢量预测值对应的点作为下一搜索步骤的起始点。

表1 当前块模式与其运动矢量预测值的候选值间的关系

（2）非对称十字形搜索（Unsymmetrical-cross search）

如图3中step2所示，由上三角标注非对称十字形，非对称是指水平方向的搜索点多于垂直方向的搜索点，这是因为自然图像序列的水平方向运动多于垂直方向的运动，所以水平方向的搜索范围为W=16，垂直方向的搜索范围为W/2=8，当图像中垂直方向的运动多于水平方向的运动时也可将垂直方向的搜索点扩展至W，搜索点间距为2。具有最小代价的运动矢量将作为下一搜索步骤的搜索中心。非对称十字形搜索可以近乎准确的给出最佳运动矢量。

（3）不均匀多层六边形网格搜索（Uneven Multi-Hexagon-Grid Search）

分为两步：

第一步，由图2中step3-1所示，由红色圆点标注，围绕搜索中心的搜索范围为2的全搜索；

第二步，由图2中step3-2所示，由非填充矩形标注，以第一步搜索所得最优点为中心进行多层六边形网格搜索。

由于自然图像序列中水平方向的运动多于垂直方向的运动，所以采用16点六边形模式（16-HP）作为基本搜索模式。多层六边形网格是由基本的16点六边形按照1到W/4的比例扩展得到，搜索时是从最里面的六边形开始直到最外面的六边形，通过这一步得到的最佳运动矢量将作为下一搜索步骤的搜索中心。

（4）扩展的六边形搜索（Extended Hexagon-based Search，EHS）

也分为两步，第一步如图3-2中step4-1所示，由下三角标注，以上一搜索步骤得到的最优点为中心进行6个点的六边形模板搜索，直到最优点位于六边形模板的中心才进入第二步，否则重复该步骤。

第二步如图中step4-2所示，由填充成黑色的矩形标注，以第一步得到的最优点为中心进行4个点的菱形搜索，直到最优点位于菱形模板的中心，该最优点即为最终的最优点。即使用上一步搜索得到的最优点为搜索中心进行六边形搜索，直到最优点位于六边形的中心，再使用菱形搜索模板进行搜索，直到最小块失真的点位于新形成的菱形的中心，搜索得到的点即为整个搜索的最优点。

2.3 SUMHexagonS

SUMHexagonS（精简的UMHexagonS算法）[3]是由Xiaoquan Yi等人在UMHexagons算法基础上改进和简化的算法，相比于UMHexagons和FS，SUMHexagonS能在实现相似甚至更好的率失真性能的情况下减少55%到94%的运动估计时间，并且与低复杂度模式下的FS算法相比，SUMHexagonS能减少18%的比特率，此外，使用SUMHexagonS产生的运动矢量更平滑，故编码运动矢量差使用的比特数减少，这对易错环境下的数据分割和不均等差错保护很有利。

（1）低内存的运动矢量预测方案

SUMHexagonS提供了一种低内存的运动矢量预测方案，即相比于UMHexagonS算法，SUMHexagonS消耗的内存更小，UMHexagonS算法使用空域、时域预测和上层预测对运动适量及SAD进行预测，这些都需要消耗很大的内存，并且H.264/AVC多种块大小、多参考帧及1/4像素精度的运动补偿等技术使得时域预测消耗的内存最大， 这对内存受限的应用极其不利。SUMHexagonS提供的低内存运动估计预测方案为：对于运动矢量预测，只使用空域中值预测和上层预测，对于SAD预测，相比于UMHexagonS算法使用4种预测方法，SUMHexagonS只使用上层预测。仿真结果表明，SUMHexagonS使用这种低内存运动估计预测方案能达到和UMHexagonS算法近乎相同的性能。

UMHexagonS算法使用局部全搜索和十字形、钻石（菱形）、六边形和大六边形等多种形状模板来避免陷入局部最优，尽管使用了基于量化参数的提前终止技术，但仍然会耗费很多时间，同时，获得门限值会对每个搜索块进行浮点计算，这更加耗费时间。SUM HexagonS避免了使用局部全搜索，并且使用了简化的提前终止技术。

SUMHexagonS流程如下[3]：

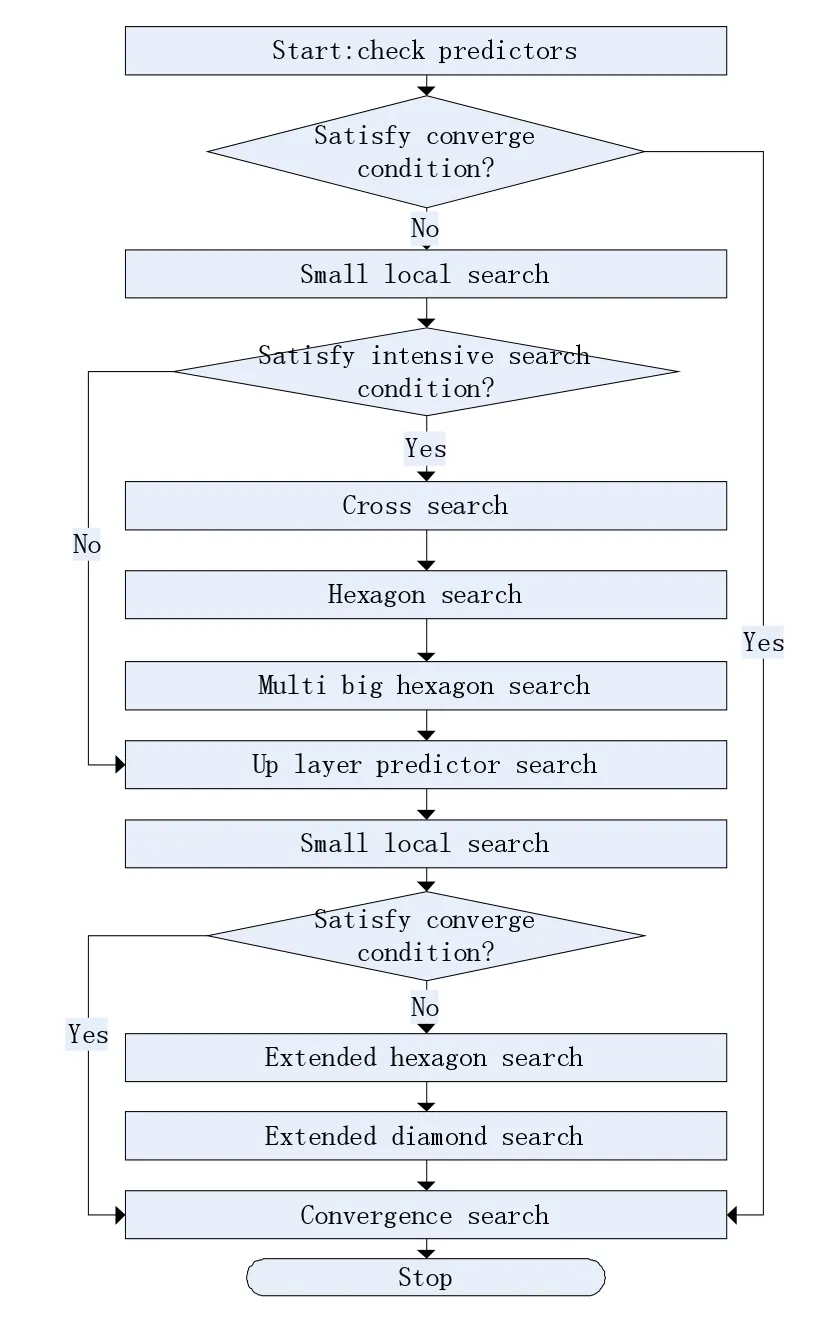
图3 SUMHexagonS流程

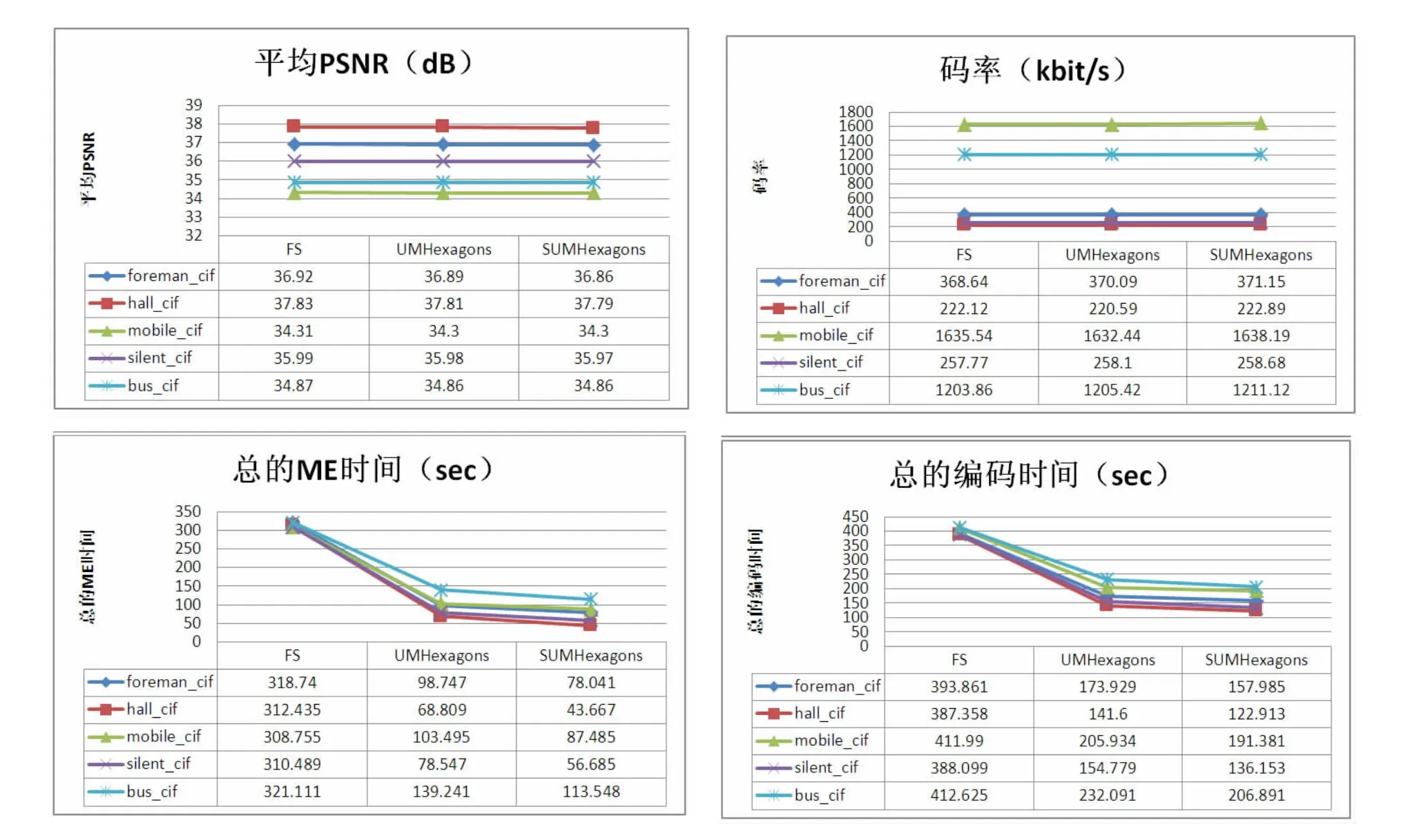
图4 每个视频序列不同算法性能对比

（2）简化的提前终止技术

SUMHexagonS将提前终止技术门限的初始值设置如下：

CrossSearchThreshold1=800，CrossSearchThreshold2 =7000，and ConvergeThreshold=1000，对于不同大小的块可以通过简单地移位操作来获得这些门限值，相比与先前使用浮点乘法的提前终止技术，SUMHexagonS使用简单的移位和比较将其简化。

3 实验结果及分析

3.1 测试环境

测试用软件：H.264参考软件JM，版本为JM10.1[4]

画图软件：MATLAB版本7.11.0.584（R2010b）32位（Win32）

测试用PC：处理器为Intel Core i3 CPU M 370@ 2.40GHz 2.40GHz，内存为2.00GB（1.86GB可用），操作系统为Windows 7旗舰版32位操作系统

测试用序列为CIF格式（352×288，YUV 4:2:0），使用H.264基本档次进行编码，配置文件参考基本档次配置文件encoderbaseline.cfg，保持大部分参数不变，只改变了其中几个参数：

使用不同的运动估计算法UseFME的值不一样

图5 使用bus_cif序列对3种算法以帧为单位进行比较

3.2 结果与分析

首先从平均PSNR、码率、总的ME时间（总的运动估计时间）、总的编码时间4个方面使用5个测试视频序列对3个算法：全搜索算法（FS）、UMHexagonS算法及SUMHexagonS算法进行了统计和对比，如图1所示。

相对于FS，两种优化算法在平均PSNR只降低0.01到0.06的范围内，使运动估计时间降低56.64%到86.02%。

另外，还从PSNR、运动估计时间（MET）、编码使用比特数、编码总时间4个方面对3个算法基于帧进行了分析，下面为运动比较剧烈的测试视频序列buscif（CIF，352×288）的实验结果:

从实验结果可以看出优化的运动估计算法UMHexagonS算法和SUMHexagonS算法在保持PSNR基本不变的情况下大大减少了运动估计时间和整体的编码时间，并且编码每帧使用的比特数基本不变。

4 结语

通过对上述几种典型运动估计算法的详细分析，总结出运动估计过程最关键的几步为：确定搜索窗口的大小、形状、位置，选择搜索起始点，选择块匹配准则，确定搜索策略。优化方法都是相对于全搜索算法减少总的搜索点数，UMHexagonS算法在搜索起始点和搜索策略等方面对先前算法进行了改进，使用了搜索起始点预测、提前终止和多种搜索模板混合使用的技术，大大减少了运动估计的时间。SUMHexagonS算法在UMHexagonS算法的基础上减少了搜索起始点预测的预测方法，简化了提前终止技术，使用简单的移位和比较技术设置提前终止的门限值，大大减少了原来使用浮点乘法实现的计算量。我们以后对运动估计算法的优化也可以从搜索起始点、搜索策略方面进行改进，同时也可以从搜索窗口的大小、块匹配准则等方面对其进行优化。

参考文献：

[1]Chen Z，Zhou P，He Y.Fast Integer Pel and Fractional Pel Motion Estimation for JVT[J].JVT-F017，2002:5-13.

[2]Chen Z，Zhou P，He Y.Fast Motion Estimation for JVT.JVT-G016.doc，Joint Video Team（JVT）of ISO/IEC MPEG&ITU-T VCEG [C].7th meeting，Pattaya，TH（March 5-13，2003），2003.

[3]Yi X，Zhang J，Ling N，et al.Improved and Simplified Fast Motion Estimation for JM[C].JVT-P021.doc，Joint Video Team（JVT）of ISO/IEC MPEG&ITU-T VCEG，16th meeting，Pozan，Poland.2005.

[4]JM参考软件http://iphome.hhi.de/suehring/tml/

Comparison and Analysis of H.264 Motion Estimation Algorithms

LIU Shu-ping
（College of Computer Science，Sichuan University，Chengdu 610065）

Studies several typical motion estimation algorithms in H.264/AVC encoder,and tests these motion estimation algorithms with the basic test video sequence.The experimental results show that the optimized motion estimation algorithm UMHexagonS and SUMHexagonS greatly reduce the motion estimation time and the overall coding time while PSNR and the number of bits used per frame are almost unchanged.At the same time,summarizes the optimization direction of the motion estimation algorithm,which lays the foundation for the future optimization.

Motion Estimation;Full Search;UMHexagonS;SUMHexagonS;PSNR

1007-1423（2017）09-0041-06

10.3969/j.issn.1007-1423.2017.09.011

刘书平（1991-），女，四川简阳人，硕士研究生，研究方向为图形图像技术

2017-01-12

2017-03-10