考虑时效性的铁路货运定价模型

李菲菲

(运城学院 经济管理系,山西 运城 044000)

理论经济研究

考虑时效性的铁路货运定价模型

李菲菲

(运城学院 经济管理系,山西 运城 044000)

我国铁路货运价格体系长期以来实行以距离和重量为基础的运价结构,但是随着货运市场的竞争日益激烈,货主对货物运输的要求越来越高,其中时效性因素已经越来越不容忽视。在研究货运定价模型的过程中引入了时效性因素,以期能够使得我国的铁路运输部门在市场竞争中提高竞争力,争取更多货源。

铁路货运;时效性;定价模型

一、引言

铁路货运定价问题一直都是收益管理的一个重要方面,目前关于铁路货运定价的相关文献很多。Chris Nash、Cesar Rivera提出了针对欧洲铁路市场的铁路运价改革方案,Anne Yvrande、Billon根据英国铁路货运市场状况,研究了其改革过程中遇到的问题并指出了适合其发展的铁路改革模式[1]。徐刚根据优化理论建立了铁路货运市场价格模型[2],李云清分析了现行铁路快捷货物运输定价方面存在的相关问题,并据此提出了相关的建议[3]。陆桂芬在研究铁路货运定价模型中引入了运输需求、竞争状况、货主承受能力等因素[4],杜慧峰则在研究铁路货运定价问题时引入了竞争的方法[5]。

结合以上文献可以发现,这些文献在研究铁路货运定价问题时都没有考虑时效性因素,而随着市场竞争的日益加剧,货物运输的时效性越来越不容忽视,因此有必要在现有研究的基础上考虑货物运输的实效性因素。

二、符号定义

将货物按不同的等级、不同的运输时效性进行分类,并将时效性分为不同的等级。将货物运输时间划分为不同的周期,每一周期为5天,即T=5天。

各符号定义如下:

tn为货物销售周期第n天,qk,l(tn)为第k等级l等级时效性的货物在tn时刻的运输量,Qk,l(tn)为第k等级l等级时效性的货物在tn时刻的运能,pk,l(tn):第k等级l等级时效性的货物在tn时刻的运输价格,λk,l(tn)为第k等级l等级时效性货物潜在货主申请请求车概率。

三、模型的构建

1.收益模型的构建

(3)运输条件的不同也会对价格产生影响,可以将价格表示为pk,l=pki,l+λcki,lpki,l,其中i表示货物运输的条件，则pki,l表示k等级采i种运输条件，l等级时效性货物的价格，cki,l表示k等级采用i种运输条件、l等级时效性货物价格加成百分比。

运输条件的不同情况有:冷藏车相比普通货车消耗能源多要求条件高,所以价格也会不同;特种平车使用率不高,因此会加收额外使用费;限速、超限、超长货物在通行时会对通行区间造成一定影响,降低铁路运输收益,因此价格也应适当高些;危险货物有特定的运输条件,会增收相应费用。

s.t

pk,l=pki,l+λcki,lpki,l,

(i∈ω时,λ=1;当i∉ω时,λ=0)

p>0,tn≤T.

2.货物运输量qk,l的确定

货主选择不同的时效性会获得不同的效用值,将其设定为一个随机变量,可以表示为:Uk,l(tn)=Vk,l(tn)+εk,l(tn).其中Uk,l(tn)、Vk,l(tn)分别表示在不同时刻选择不同等级不同等级时效性的货物获得的随机效用值及可确定的效用值,εk,l(tn)表示在tn时刻的随机误差。

在申请请求车时,货主会根据具体情况选择不同等级不同等级时效性的货物,本文采用logit模型来描述这种选择的概率,如下所示:

式中β为校正参数。

根据Prk,l(tn)可以得出在不同时刻不同等级不同等级时效性的货物申请请求车的需求Dk,l(tn)及货物运输量qk,l(tn)分别如下所示:

Dk,l(tn)=D(tn)Prk,l(tn),

qk,l(tn)=Dk,l(tn)λk,l(tn).

其中D(tn)表示在tn时刻某站的总货运需求。设货主选择不同的运输方式有不同的广义费用,本文采用幂函数形式描述广义费用函数:

f(x)=a·xb-Vi,i=1,2,…,21.

其中,a和b为待定参数,Vi表示不同运输方式的效用。

构建广义费用最小模型如下所示:

s.t

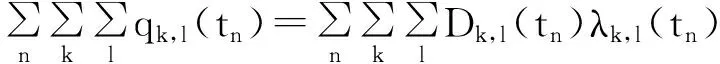
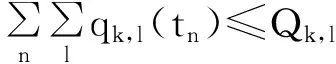
qk,l(tn),Qk.l(tn)≥0.

3.双层规划模型的建立

通过上述两个模型可以得到铁路货物运输价格优化问题的双层规划模型:

s.t

pk,l=pki,l+λcki,lpki,l

(i∈ω时,λ=1;当i∉ω时,λ=0,

p>0,

t,n≤T

s.t

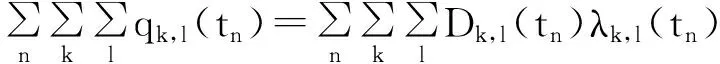
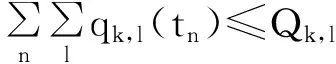
qk,l(tn),Qk.l(tn)≥0.

四、算例分析

由于数据的可获得性差,本文采用算例分析的方式,并且采用遗传算法对模型进行求解。

本文只考虑整车货物运输方式,按照货物的运价号将货物品类分为7种等级,将时效性因素分为3个等级,分别为特快、快速、普快,时效性依次降低。对于一个特定货运站来说货物运输方式如图1所示。

1.算例相关参数的设定

用幂函数描述广义费用函数:

f(qi)=a(qi)b-Vi, i=1,2,…,21.

假定a=3,b=0.7;Vi为效用函数,可表示为:

Vi=-α1ti-α2pi+α3ci, i=1,2,…,21.

其中ti、pi、ci分别为运输时间、价格、安全性因素;αk(k=1,2,3)为待定参数。

效用参数如表1所示。

参数α,a,b的取值如下:α1=0.3;α2=0.6;α3=0.2;a=3;b=0.7;c=0.001 5。申请请求车的到达率如表2所示。

假设该站预测需求量如下:第一天1 300,第二天2 500,第三天3 900,第四天1 400,第五天2 300。

已知政府限定的运输价格上下限分别为:

图1 运输方式结构图

运能限制如下:运输方式1的运能为360,方式2为360,方式3为300,方式4为460,方式5为400,方式6为300,方式7为580,方式8为510,方式9为440,方式10为700,方式11为640,方式12为630,方式13为1 100,方式14为900,方式15为600,方式16为690,方式17为525,方式18为400,方式19为655,方式20为452,方式21为390。

2.算例结果分析

采用遗产算法编程结果如表3、表4所示(其中T=1 000代)。

参数α,a,b的取值如下:α1=0.3;α2=0.6;α3=0.2;a=3;b=0.7;c=0.001 5。申请请求车的到达率如表2所示。

从表3、表4中不难发现,不同等级的货物在不同时效性下价格会不同,并且货物运输需求量会使得不同时间的货物运输价格不同。考虑货物运输时效性因素后铁路运输部门可以实现最大收益5 661 600.33。

采用遗传算法运行10次,算法的收敛效果良好,稳定性很好。

本文针对目前铁路货运市场的实际状况适时考虑了货物运输的时效性因素,据此建立了以收益最大化为目标和基于logit选择的双层规划模型,并采用遗传算法进行求解。最后通过算例分析得到模型的有效最优解,并证明遗传算法的稳定性和收敛性很好。

表1 效用参数表

表2 不同运输方式不同时刻的请求车到达率

表3 算例计算结果(运输价格)

表4 算例计算结果(销售数量)

续表4 算例计算结果(销售数量)

[1]Anne Yvrande Billon,Claude Menard.Instituional constraints and organizational changes:the case of the British rail reform[J].Journal of Economic Behavior Organization,2005,(4):44-58.

[2]徐刚.铁路货物运输市场价格优化模型研究[J].中国铁道科学,2003,24(1):12-13.

[3]李云清.我国铁路快捷货物运输定价策略研究[J].价格理论与实践,2009,(6):11-13.

[4]陆桂芬.我国铁路货运定价模型[D].北京:北京交通大学,2013.

[5]杜慧峰.铁路货运定价机制中的竞争因素分析[J].现代经济信息,2014,(18):23-24.

[责任编辑:陈宇涵]

10.3969/j.issn.1672-5956.2017.01.009

2016-10-08

李菲菲,1987年生,女,山西运城人,运城学院助教,硕士,研究方向为物流工程,(电子信箱)511935220@qq.com。

F532.5

A

1672-5956(2017)01-0060-06