基于波段指数的快速高光谱图像波段选择方法

孙康 陈金勇

（中国电子科技集团公司第五十四研究所，石家庄，050081）

基于波段指数的快速高光谱图像波段选择方法

孙康1陈金勇1

（中国电子科技集团公司第五十四研究所，石家庄，050081）

波段选择在高光谱图像降维处理领域具有十分重要的作用，可以提高高光谱图像的分类精度。波段选择本质上是最优波段的组合优化问题，因而往往具有较高的计算复杂度，限制了波段选择技术在高光谱图像中的应用。本文提出了一个基于协方差矩阵的快速波段选择方法，该方法波段选择的目标是具有最大协方差矩阵行列式的波段集合。利用本文提出的一个前向递推迭代技巧和波段指数，该方法具有极快的计算速度。此外，本文提出的波段指数还具有指示波段选择所需波段数目的能力。

高光谱图像，降维，特征提取，波段选择，协方差矩阵

一、引言

高光谱图像具有较大的数据体量，一般包含数百个连续的窄波段，因此在传输、储存、计算以及统计建模等方面带来很大的挑战[1]。降维是解决高光谱维数灾难问题的一个有效手段，因此近年来获得越来越多的关注和研究。

广义上，根据原始特征和提取特征之间的关系，高光谱降维方法可以分为两大类型：特征提取和特征选择（也称波段选择）。特征提取通过原始特征的函数映射（一般为线性函数）或组合获得新的特征，典型的方法有主成分分析、最小噪声分离以及独立成分分析等。这类方法的缺点是由于新的特征是原始特征的变换，因此破坏了原始光谱特征的物理意义，使得提取的特征不具有物理意义[2]。

另外一种典型的高光谱降维方法是波段选择。波段选择与特征提取最大的不同在于，它是通过选择原始特征的子集来达到降维的目的，并没有产生新的特征。与特征提取相比，波段选择有两个主要的优点：一是，波段选择得到的特征具备更强的物理意义；而是波段选择对于高光谱数据获取（比如对于动态可配置的传感器）、数据传输和数据储存都具有重要意义。

本质上，波段选择是一个组合优化的问题，一般而言具有极高的计算复杂度。由于波段选择的主要目的之一是降低高光谱图像处理的计算负荷，如何尽量降低波段选择本身的计算复杂度显得尤为重要。目前已经有较多的研究聚焦于降低波段选择的计算复杂度。比如，杨河等[3]提出使用GPU实现一个基于相似度量的波段选择方法[4]；耿修瑞等提出了利用体积梯度降低波段选择的计算复杂度[5],；孙康等提出了基于典型成分分析的波段选择方法ECA[6]，着重研究了波段选择算法的计算复杂度问题[7]。

本文提出了基于协方差矩阵的波段选择方法FCMBS。FCMBS波段选择的目标是具有最大协方差矩阵行列式的波段集合。利用本文发现的一个迭代规律，FCMBS不仅大大降低了行列式的计算复杂度，同时还可以辅助确定波段选择所需波段数目。

二、波段选择准则函数

波段选择通常包含两个典型步骤：准则函数（目标函数）确定以及子集搜索。准则函数波段选择的依据，定量地描述了波段选择的条件；子集搜索是选择使得目标函数具有最优取值的波段集合。目前有很多的波段选择准则函数，其中最经典的一个是由Sheffield提出的最大椭球体体积准则（MEV）)[8]，作者同时证明了MEV等价于协方差矩阵的行列式。更近一步地，已经证明，选择协方差矩阵行列式最大的波段子集完全等价于选择具有最大联合熵的波段子集。MEV准则函数如下：

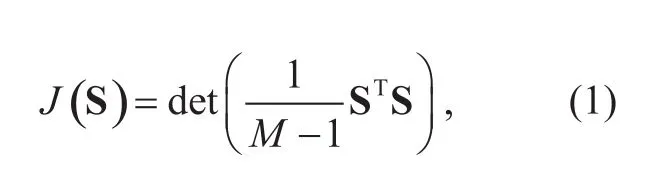
尽管具有完备的理论基础以及出色的应用效果，MEV的一个重要缺点是计算复杂度极高。MEV原本是用于多光谱图像波段选择的方法，从7个波段中选择3个波段用于彩色合成，总共个波段组合。这种情况下，使用穷举搜索的方法可以很快地得到最优解。然而对高光谱图像而言，穷举搜索的计算复杂度是不可能完成的。比如AVIRIS图像具有224个波段，如果从中选择15个波段，则总共可能的波段组合共计个，这样的计算复杂度对于目前的计算机而言是不可能完成的。解决这个问题的方法是使用搜索方法得到次优解，达到效率与效果的折中。常用的搜索方法包括序贯前向搜索（SFS）以及序贯后向搜索（SBS）。对MEV而言，由于涉及到频繁的协方差矩阵矩阵，即使使用SFS进行搜索，所需要的计算复杂度也是难以接受的。

三、子集搜索和选择指数

本节介绍本文提出的FCMBS算法，FCMBS使用MEV的准则函数，但具有极低的计算复杂度，同时具有辅助确定所需的波段数目的能力。FCMBS波段选择的准则函数与（1）相同，忽略常数项该准则可以简化为：

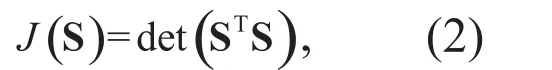
FCMBS使用SFS进行子集搜索。SFS是贪婪算法的一种，更具体地，它是一个“自下而上”的算法，开始选择一个波段，而后逐个增加选择的波段，直至波段的数目符合要求。FCMBS需要先选择一个波段作为初始解。本文选择具有最大方差的波段作为入选的第一个波段，剩下的个波段依次作为第二个波段，这样共产生波段个双波段组合。根据式（2），这个双波段组合中，具有最大协方差矩阵行列式的组合作为入选组合。这 个过程一直重复，直至入选的波段数目达到预先设置的数目。

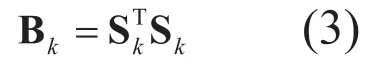
可以看出，第 和 阶协方差矩阵 和 具有如下迭代关系：

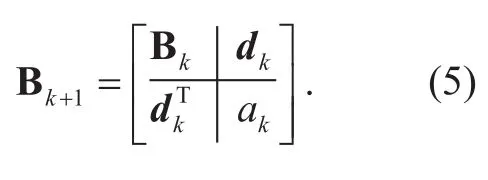
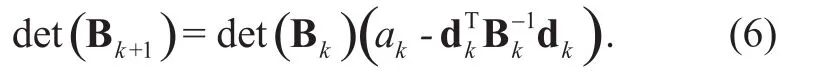
从式（6）中可以发现，当已经选择 个波段是，第 个入选的波段是使得取最大值的波段。由于对于剩余的波段而言是一个常数，因此是项决定了下一个入选的波段。由于该项定量描述了波段的入选可能性，本文将项定义为波段的选择指数（SI）。SI的使用使得FCMBS无需计算复杂的协方差矩阵，因此计算复杂度大大降低。同时本文发现SI随着入选波段数目的增加呈单调下降，这个规律可以用来确定波段选择所需的波段数目。SI的这个性质将于第5节详细探讨。

四、计算复杂度分析

本节主要对比分析FCMBS以及直接采用SFS的MEV算法（SFS-MEV）的理论计算复杂度。

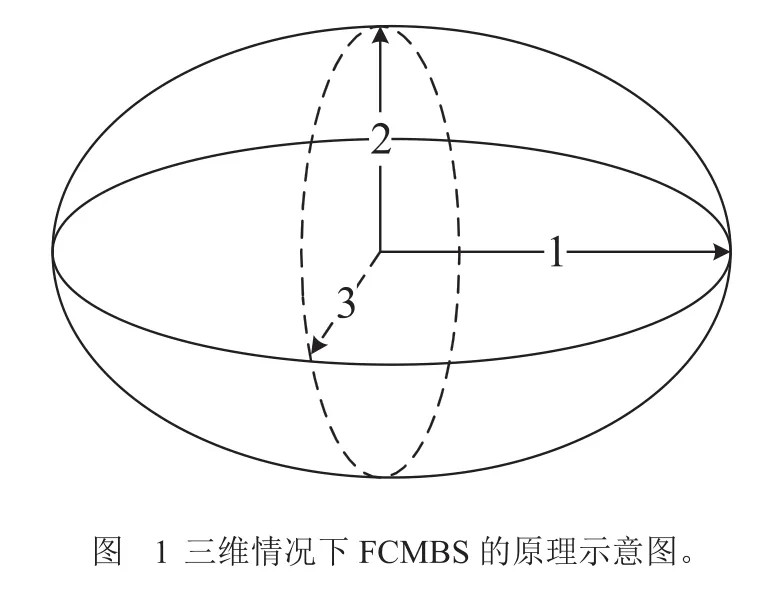
根据文献[8]，的行列式在几何意义上等于所构成的高维椭球体的体积，以此类推，相当于和构成的高维椭球体体积。根据式（6）所示和的关系，可以看出，选择指数事实上就是构成的超平面的距离。图1给出了三维时的情况，假定现已选择了两个波段，这两个波段构成的椭球体是有轴1和轴2张成的椭圆。根据FCMBS的最大行列式（等价于最大体积）规则，第三个选择的波段就是能与前两个波段构成最大椭球体积的波段，也就是距离前两个波段构成的椭圆最远的波段。

综上，可以看出FCMBS与SFS-MEV的本质区别在于，FCMBS只需计算距离，而SFS-MEV需要计算体积，因此FCMBS具有极大的效率优势。经过简单的定量分析可以得到，FCMBS需要的浮点操作次数而SFS-MEV需要的浮点操作次数为从理论上，FCMBS的计算速度是SFSMEV的倍。

五、试验分析

为了定量评估FCMBS方法的实际性能，本文使用由美国AVIRIS传感器获取的真实的高光谱数据-Indian Pines数据。该数据空间大小为145×145像素，包含220个波段，波段范围是400-2500nm。由于具有像素级的地面真值并且在互联网可以免费下载，该数据广泛应用于各类遥感试验。根据地面调查结果，这块数据共包含16种不同的地物类型，如图2所示。

5.1 波段选择精度与计算时间比较

利用虚拟维数方法，可以确定这块数据的维数为16，因此本试验将波段选择数目设置为16。为了对FCMBS的性能进行评价分析，本试验选择IDBS[9]，MVPCA[10]以及SFS-MEV作为对比方法。分别比较各个波段选择方法的波段选择精度和计算时间。波段选择精度的比较一般采用波段选择后的分类精度进行比较，本文使用SVM方法进行分类，训练样本根据图2（b）所示的地面真值进行随机选取，训练样本比例为10%，SVM核函数为RBF函数。波段选择时间采取10次平均的方法计算得到。各个波段选择方法获取的分类精度和计算时间如图3所示的双轴图。

从图3中可以看出，本文方法FCMBS和SFS-MEV的分类精度一致并且最高（66.5%），因为二者的波段选择结果相同，但FCMBS的计算时间仅为0.12s，远远小于SFS-MEV的计算时间（4.91s），其加速比约为40倍。与IDBS和MVPCA相比，FCMBS的波段选择结果具有更高的分类精度，分别比IDBS和MVPCA高出10.7百分点和4.2百分点。同时，FCMBS的计算时间也优于这两个波段选择方法，对IDBS和MVPCA的计算时间加速比分别为16.6和3.7。

整体看来，对传统方法相比，FCMBS能够获得更高的分类精度，同时具有明显的加速效果。

5.2 SI的进一步探讨

对于选择指数SI，本文还发现了一个有趣的现象，也即随着选择波段数目的增加，SI成单调下降趋势，如图3所示。从图中可以看出，当波段数目较小时，SI下降速度很快，而后逐步趋缓。在SI曲线中，有一个明显的拐点（大约是16波段，图中红点所示），这个拐点与虚拟维数的结论基本一致。在拐点以前，SI下降速度非常迅速，而在拐点之后，SI趋于平缓。因此，SI可以看出是度量波段的重要程度的指标，最重要的波段第一个被选出，而后选出的波段依次下降，当拐点出现的时候，意味着已经选择了足够多的波段。这样SI事实上可以辅助确定所需的波段数目。

六、结论

本文提出了一个新的波段选择方法FCMBS，该方法的选择准则是最大协方差矩阵行列式。利用本文新定义的选择指数SI，FCMBS不仅大大减少了计算复杂度，同时可以辅助确定具有波段选择所需的波段数目。试验结果验证了本文方法的高效性以及确定波段数目的能力。

[1]K.Sun,X.Geng,L.Ji,and Y.Lu,"A new band selection method for hyperspectral image based on data quality,"Selected Topics in Applied Earth Observations and RemoteSensing,IEEE Journal of,vol.7,pp. 2697-2703, 2014.

[2]M.Vélez-Reyes,D.M.Linares,and L.O.Jiménez, "Two-Stage Band Selection Algorithm for Hyperspectral Imagery,"presented at the Algorithms and Technologies for Multispectral,Hyperspectral,and Ultraspectral Imagery VIII,Proceedings of SPIE,Orlando, Florida,2002.

[3]H.Yang,Q.Du,and G.Chen,"Unsupervised hyperspectral band selection using graphics processing units,"Selected Topics in Applied Earth Observations and Remote Sensing, IEEE Journal of,vol.4,pp.660-668, 2011.

[4]Q.Du and H.Yang,"Similarity-based unsupervised band selection for hyperspectral image analysis,"Geoscience and Remote Sensing Letters,IEEE,vol.5,pp.564-568,2008.

[5]X.Geng,K.Sun,L.Ji,and Y.Zhao,"A fast volume-gradient based band selection method for hyperspectral image,"Geoscience and Remote Sensing,IEEE transactions on,vol.52, pp.7111-7119, 2014.

[6]K.Sun,X.Geng,and L.Ji,"An efficient unsupervised band selection method based on an autocorrelation matrix for a hyperspectral image,"International Journal of Remote Sensing,vol.35,pp.7458-7 476,2014.

[7]K.Sun,X.Geng,and L.Ji,"Exemplar component analysis∶a fast band selection method for hyperspectral imagery,"Geoscience and Remote Sensing Letters,IEEE,vol.12,pp.998-1002,2015.

[8]C.Sheffield,"Selecting Band Combinations from Multispectral Data,"Photogrammetric Engineering and Remote Sensing,vol.51,pp. 681-687,1985.

[9]C.-I.Chang and S.Wang,"Constrained band selection for hyperspectral imagery," Geoscience and Remote Sensing,IEEE Transactions on,vol.44,pp.1575-1585,2006.

[10]C.-I.Chang,Q.Du,T.-L.Sun,and M.L.Althouse, "A joint band prioritization and banddecorrelation approach to band selection for hyperspectral image classification," Geoscience and Remote Sensing, IEEE Transactions on,vol.37,pp.2631-2641,1999.

河北省遥感中心《2014年度河北省海洋环境遥感监测》项目入选中国遥感应用协会科技进步奖三等奖

根据《关于确定中国遥感应用协会科学技术奖奖励办法》（暂行）,中国遥感应用协会2016年6月面向各分支机构和会员单位征集申报项目；8月27日至28日组织中国遥感应用协会科技进步奖评审委员会审查申报项目，形成了获奖候选项目建议；9月至12月经征求各候选项目申报单位意见，形成一等奖候选项目1项、二等候选项目3项和三等奖候选项目5项。2017年3月3日己将将上述九项候选项目的相关情况提交给中国遥感应用协会科学技术奖奖励委员会各位委员审议。河北省遥感中心《2014年度河北省海洋环境遥感监测》项目入选三等奖并已公示。该项目应用于区域性海洋水色水温环境要素遥感检测技术、河北海洋海冰遥感检测与精细化海冰分类技术、区域性秦皇岛微微藻褐遥感检测及赤潮的预警值。项目成果被河北省海洋环境监测中心、河北省海洋预报台、昌黎黄金海岸国家级自然保护区、秦皇岛港股份有限公司、秦皇岛海洋环境监测中心站等多家单位应用。