一道高三月考题的解法分析

熊康松

湖北省武汉市黄陂区汉口北高级中学 (430300)

一道高三月考题的解法分析

熊康松

湖北省武汉市黄陂区汉口北高级中学 (430300)

每年全国各地的高考和调考试题，总会推出一些背景新颖，构思精巧，具有相当深度和明确导向的创新试题，这些试题知识面广，切入点多，征服这些试题既充满乐趣，更需要智慧和勇气．

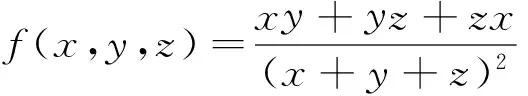
这是武汉市黄陂区第一中学2017届高三12月月考理科第10题，是一道约束条件下，多元函数的最值(范围)问题，属于创新试题，题目短小精悍，简洁有力，考察了“基本不等式”“放缩法”“构造法”等基本知识和方法，考察学生对含多个字母式子的变形能力、灵活运用不等式知识解决问题的能力、以及逻辑推理能力．从考试结果来看，学生得分率极低，解法值得研究．下面给出笔者的一些思考：

法1：(排除法)由于是选择题，“小题不能大做”，解题时若结合备选答案，灵活运用“排除法”“特例法”“代入法”“极限法”“估值法”等解题策略可达到事半功倍的效果．

法2：(放缩法)放缩法是求解和证明不等式问题最常见和最重要的方法，放缩得好，解题往往简洁明了，本题中三角形的三边需满足三边关系x+y>z，y+z>x，z+x>y，应用这一条件放缩，是解题的关键．

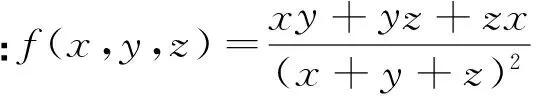
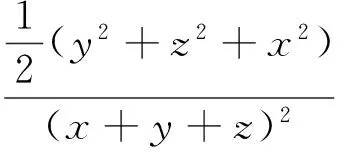
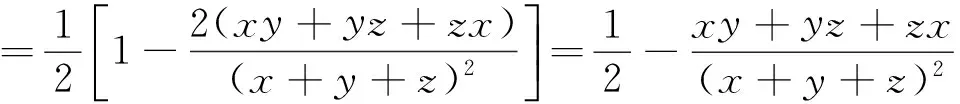
法3:(换元法)若x,y,z为三角形的三条边，则令x=a+b，y=b+c，z=a+c(a>0,b>0,c>0)，这是一种重要的换元方法(其中a,b,c表示三角形各顶点到三角形内切圆各切点的切线长)．

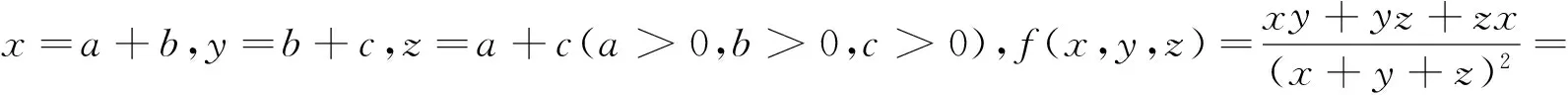
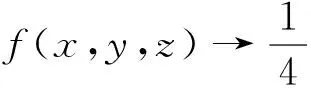
法4：(主元法)含有多个变量的函数，可以将其中某个变量当做“元”，其它变量看作常数，将问题转化为一元函数来研究，这是一种通法.

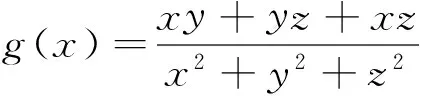
点评：先将函数的自变量看作x，把y,z当作常数，借助单调性在求出g(x)的下界确为g(y+z)后，再来研究式子g(y+z)的范围，此时再将y,z看作变量，这样就达到了将难点分步化解，各个击破的目的，解题过程中让变量“先静再动”，体现了“以静制动”的策略．

本题的后三种方法看似容易，其实不然，解题中我们要反思：为什么要这样做？不这样做不行吗？还有没有更加简单的解法？这或许是很值得进一步思考的问题，要知道，我思故我在，且行且思，任何看似偶然的技巧背后，都有其必然．