一个平面向量数量积的多种解法

胡周华

江苏省启东市汇龙中学 (226200)

一个平面向量数量积的多种解法

胡周华

江苏省启东市汇龙中学 (226200)

江苏考试说明中都将“平面向量的数量积”作为考查的重要内容(C级要求)．如果在解答题中未曾考查，那么必在填空题中考到．

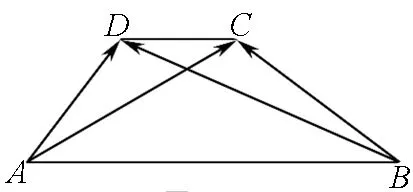
图1

向量有字母表示及坐标表示两种方法，使得向量运算持有平行的两条运算途径——向量法及坐标法，应合理地选用运算方法及它们的转化．

分析1:平面向量的基本定理说明，平面内两个不共线向量为基底可以表示任一向量，这样的基底有无穷多组．一般选用从同一顶点出发的基底向量、或首尾相连的向量，运用向量加、减法运算及数乘运算来求解，即利用相等向量、相反向量和线段的比例关系，运用运算法则，利用三角形中的中位线、相似三角形对应边成比例等，把已知向量转化为与未知向量有直接关系的向量．利用基底法和向量数量积的定义将所求向量数量积转化为已知基向量的向量数量积.

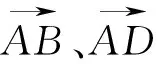
分析3:用已知向量来表示另外一些向量是用向量解题的基本要领．除利用向量的加减法、数乘外，还应充分利用平面几何的一些定理．因此，在求向量时，要尽可能转化到平行四边形或三角形中去，利用向量平移将未知向量转化为已知向量，再利用已知向量的数量积求解.

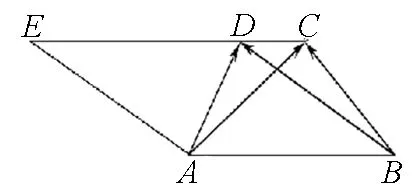
图2

分析4:建立适当的直角坐标系，将向量的运算转化为相应的坐标运算，利用向量的坐标表示把向量数量积问题数量化即坐标化.

图3

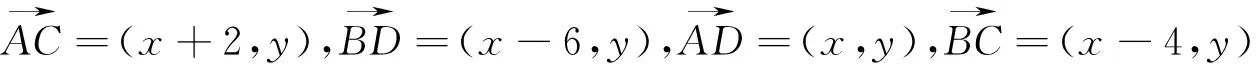
又因为AD=2，所以x2+y2=4.②

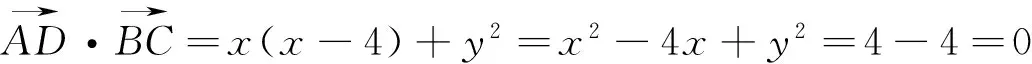
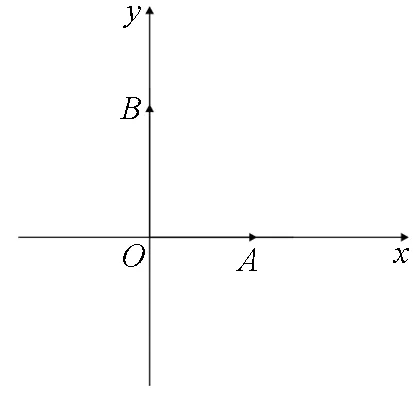
图4

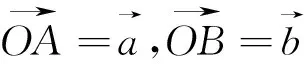
总之，求有条件的向量数量积关键是抓住条件与结论之间的关系，灵活运用向量的和差运算，促进相互之间的转化，有时要注意坐标运算，要根据题目的图形特点进行坐标选取，将向量问题代数化，也是一个很好的路径.